基于灰色-马尔科夫的马鞍山市电力需求预测分析

徐新卫, 谢尚金， 周 俊

(1.安徽工业大学管理科学与工程学院 安徽 马鞍山 243032； 2.广东科技学院管理学院 广东 东莞 523076)

0 引言

马鞍山市位于安徽省最东部，是皖江城市带连接长江黄金水道的桥头堡，同时也是承接东部发达省份产业转移示范区的门户城市，其经济发展具有很大的潜力。近年来，马鞍山市经济在持续增长的同时，社会对能源的需求也不断增加。能源是发展国民经济和提高人民生活质量的重要支柱，但由于能源的有限性，它也在一定程度上制约着国民经济的持续发展和人民生活质量的提高。电力能源作为一种非常重要的能源，在国民经济的发展和社会日常生活中具有不可或缺的作用。因此就有必要对马鞍山市的电力能源需求进行准确的预测，为区域经济发展及人民生活质量改善提供安全有效的保障。

孙涵等[1]在分析支持向量机回归 (SVR)在能源需求预测中优势的基础上，分别确定输入向量集合和输出向量集合，并构建了基于Matlab技术的SVR能源需求预测模型，对我国能源需求数据进行仿真模拟。Kran等[2]提出了一种基于粒子群优化和蚁群优化的能源需求预测混合方法并以土耳其能源需求为例进行预测。张跃军等[3]针对我国能源需求系统非线性、数据少以及能源需求影响因素众多等特征，引入支持向量机模型 (SVM)对北京市能源需求进行预测，分析其能源需求变化趋势。付立东等[4]为预测我国的能源需求，提出了一种新的遗传算法(GA)与模拟退火算法(SA)混合的方法，预测了中国在2015年和2020年的能源需求量。李剑波和鲜学福[5]结合灰色系统GM(1,1)和BP神经网络两种方法的各自优势，利用灰色神经网络模型对重庆“十三五”期间能源的消费需求进行预测。路亮等[6]通过对灰色预测、自回归移动平均模型(ARIMA)及多元回归法3种数据预测方法的分析，提出基于马尔科夫链的能源需求结构预测模型，对西南地区的能源需求进行预测，实例预测了十三五、十四五西南地区的能源需求总量。在电力的需求预测方面，陈章潮和熊岗[7]从基础理论上分析了灰色预测GM(1,1)模型的应用条件，并将其应用在上海浦东新区的电力需求长期预测中。蔡安宁和赖斯[8]以我国用电量的历史数据 (2000—2008年) 为样本, 根据灰色动态预测模型GM(1,1)的建模方法, 建立了电力需求的预测模型，对我国电力需求进行预测。Carolina和Carlos[9]为了预测西班牙未来2年的每月每小时的电力需求，提出一种考虑适用于区间时间序列的向量自回归预测模型和适用于区间数据的多层感知器模型的新预测方法。Wang等[10]通过时滞嵌入定理重构描述非线性系统行为演化的相空间，进而采用最大Lyapunov指数预测法(LLEF)法对混沌时间序列进行预测，同时为克服LLEF法的缺点，提出一种利用粒子群优化算法(PSO)确定最优权值的加权LLEF方法提高预测精度，对电力需求预测趋势进行调整研究。董力通等[11]考虑多种因素对电力经济发展弹性系数的影响, 将投入产出模型与SVM相结合，构建需求预测模型，对我国电力需求进行预测研究。Boroojeni等[12]提出一种用于电力需求预测的结合自回归(AR)和移动平均(MA)分量分别对负荷数据的非季节性和季节性周期进行建模的方法，并研究了从短期到中期的变化过程。丁珩[13]等采用Logistic模型对湖北省电力需求量和最大负荷的长期发展动向进行预测，得出湖北省未来一定时期内电力需求饱和规模和时间点。He等[14]人提出了基于新经济法的系统动力学城市长期电力需求预测方法。田星等[15]从宏观和微观层面两个维度出发，分析经济新常态下的电力需求的趋势，利用动态灰色Verhulst模型对宁夏未来用电需求做出预测。孙爱民[16]在运用GM(1,1)模型对西安市年电力需求量预测预测的基础上，建立新陈代谢GM(1,1)模型，在一定程度上提高了模型精度，并对对西安市未来5年的全年电力需求量进行预测。

我国的电力需求统计数据具有数据少、非线性，在很大程度上具有不确定性等特征。而灰色预测模型突破了一般预测建模方法需要大样本数据的局限，只需要小样本数据就能快速建模进行预测，但是当样本数据波动较大时，其预测结果则存在拟合度差、预测精度低的问题。相反马尔科夫模型能够较为精确地预测波动性强的随机样本数据，有效提高预测数据的拟合度。因此本文将二者相结合，构建灰色-马尔科夫模型，实现优势互补相辅相成，对马鞍山市的电力能源需求进行预测分析。

1 灰色-马尔科夫模型的构建

1.1 灰色预测模型的建立

灰色预测基于人们对系统演化不确定性特征的认识，运用序列算子对原始数据进行生成、处理，挖掘系统演化规律，建立灰色系统模型，对系统的未来状态做出科学的定量预测[17]。

1.1.1 GM(1，1)模型的建立

设X(0)，X(1)为非负序列：

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(1)

(2)

其中序列X(1)是原始序列X(0)经过一次累加得到的序列，记为：1-AGO；此时把形如x(0)(k)+ax(1)(k)=b的方程，称为GM(1,1)模型的原始表达形式。

设序列Z(1)为一次序列X(1)的紧邻均值生成序列

Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))

(3)

1.1.2 GM(1，1)模型的求解与还原

(4)

求解该方程，得到白化方程的解，即时间响应函数

(5)

则GM(1,1)模型x(0)(k)+az(1)(k)=b的时间响应序列即可表示为

(6)

将时间相应序列经逆向还原可得GM(1,1)模型的还原值，即预测值

(7)

其中a表示灰色模拟系统中的灰色发展系数，b为灰色作用量，即

(8)

(9)

1.2 灰色-马尔科夫过程

设原始数据序列为

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

经GM(1,1)模型进行拟合求解得到的原始样本数据拟合值为

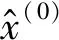
1.2.1 状态区间的划分

由样本数据的实际值与GM(1,1)模型拟合预测值的比值M合理划分状态区间，任意一个状态区间Mi的表达式为：Mi=[Mi1,Mi2]，i=1,2,…,n，其中Mi1为M的最小值，Mi2为M的最大值。

1.2.2 构建状态转移概率矩阵

(10)

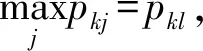
1.2.3 灰色-马尔科夫预测值的修正

利用马尔科夫链的后无效性对GM(1,1)拟合预测值进行修正与其下一步的转移状态相关，若下一步转移至状态Mj，则其修正公式为

(11)

1.3 拟合精度检验

数据拟合预测计算出结果之后，须判断其拟合值是否满足具体的使用条件，因此就需要对数据的拟合结果进行检验，分析其是否符合要求，常用的精度检验方法有以下3种。

1.3.1 平均相对误差检验

其中

1.3.2 均方差检验

1.3.3 小误差概率检验

根据拟合精度和精度检验方法的不同，导致每种检验方法都有其特定的检验标准，则具体的拟合精度参照标准如表1。

表1 拟合精度检验参照标准

2 实例分析

2.1 GM(1,1)模型求预测值

以马鞍山市2010—2019年电力需求总量为样本数据，构建原始数据序列X(0)，即X(0)=(x(0)(1),x(0)(1),…,x(0)(n))，通过查询马鞍山市各年统计年鉴得出具体数据如表2。

表2 2010—2019年马鞍山市电力能源需求总量

按照灰色-马尔科夫模型的基本构建过程进行相应的预测分析

(1)首先，根据式(1)及表2中2010—2019年马鞍山市电力能源需求总量数据建立GM(1,1)模型的初始数据序列：

X(0)=(x(0)(1),x(0)(2),…,x(0)(10))

=(130.85,138.65,148.05,158.99,170.90,178.17,188.84,197.10,205.71,214.08)

(2)由式(2)可得1-AGO序列

X(1)=(x(1)(1),x(1)(2),…,x(1)(10))

=(130.85,269.50,417.55,576.54,747.44,925.61,1114.45,1311.55,1517.26,1731.34)

(3)进一步计算得出紧邻均值生成序列Z(1)

Z(1)=(z(1)(2),z(1)(3),…,z(1)(10))=

(200.175，343.525,497.045,661.990,836.525,1020.030,1213.000,1414.405,1624.300)

(4)根据式(8)、(9)计算出a和b的值

a=-0.0528，b=-131.9944

(5)代入a和b的值，则易得GM(1,1)模型的累减还原值公式为

(12)

由式(12)计算2010—2019年马鞍山市电力需求总量GM(1,1)模型的预测值，同时计算样本数据的实际值与GM(1,1)模型拟合预测值的比值M如表3，并作图以直观化(如图1所示)。

观察表3的样本实际值与GM(1,1)模型拟合预测值的比值M可以看出比值分布在区间[0.9721,1.0226]之中，数据的预测拟合度较高。

表3 2010—2019年马鞍山市电力需求总量GM(1,1)模型模拟结果

图1 马鞍山市电力需求总量实际值与GM(1,1)模型预测值对比

2.2 灰色-马尔科夫组合预测

(1)状态区间划分

使用样本初始值与GM(1,1)模型拟合预测值的比值M划分状态区间，根据表3中的M计算结果可将其划分为4个状态区间，则每个状态区间的划分具体情况如表4所示。

(2)计算状态转移概率矩阵

根据表3数据中的M值及表4 的状态区间的划分情况，进而所构造的状态转移概率矩阵为

表4 状态区间划分结果

(3)马尔科夫对GM(1,1)模型预测值的修正

在马尔科夫链中，下一步数据的状态是由上一步所处状态通过一步转移得到。状态转移矩阵中，若在某一步的状态转移概率出现相同情况，则取各状态区间值的加权平均值。运用马尔科夫过程对GM(1,1)模型的拟合预测值修正结果如表5所示，作原始样本数据、GM(1,1)模型的拟合预测值和马尔科夫修正结果的直观对比如图2。

表5 GM(1,1)模型预测及马尔科夫修正结果

通过图2可以粗略地观察到马尔科夫修正的预测值曲线与样本初始值曲线较GM(1,1)模型曲线更加贴合，准确性更高，拟合效果更好。

2.3 模型拟合精度检验

为了更加科学客观地比较GM(1,1)模型、灰色-马尔科夫模型的模型拟合性与准确性，因此，根据已知的样本初始数据和GM(1,1)模型和灰色-马尔科夫模型得到的两种预测结果数据，对两种预测拟合结果分别进行平均相对误差、均方差及小误差概率检验，其精度检验结果如表6所示。

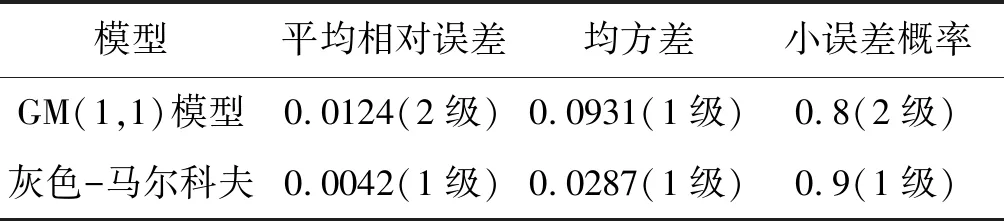
表6 GM(1,1)模型和马尔科夫修正预测精度比较

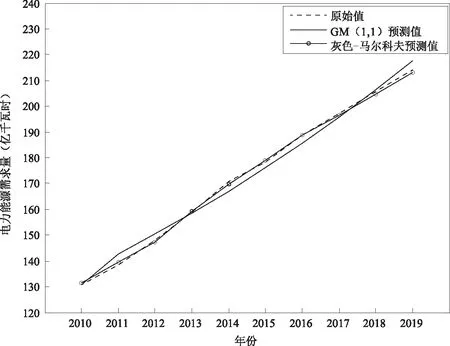
图2 初始数据与GM(1,1)和马尔科夫修正模型对比图

结合两种模型的预测结果和拟合精度检验参照标准可知，灰色-马尔科夫预测模型预测结果的平均相对误差为0.0042，比GM(1,1)模型预测结果的0.0124减少了66.13%，在模型精度等级上由2级提升到1级；在均方差检验上，虽然模型精度等级均为1级，但是，灰色-马尔科夫预测模型均方差为0.0287，相较于GM(1,1)模型均方差的0.0931减少了69.17%；在均方差检验上，灰色-马尔科夫预测模型小误差概率较GM(1,1)模型也提高了10%，模型精度等级上也由2级提升到1级。综合分析结果，充分说明灰色-马尔科夫预测模型在电力需求方面的预测要优于GM(1,1)模型。

2.4 模型预测

在2010—2019年马鞍山市电力需求总量为样本数据的基础上，利用GM(1,1)模型与灰色-马尔科夫模型分别预测2020—2022年，未来3年的马鞍山市电力需求总量。结合状态转移概率矩阵P，其状态分布预测如表7所示，根据灰色-马尔科夫预测模型基本思路来预测2020—2022年马鞍山市电力需求量如表8。

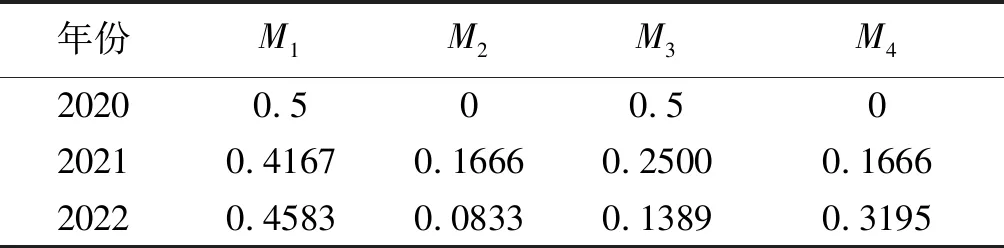
表7 2020—2022年所处状态的分布概率

表8 2020—2022年马鞍山市电力需求量预测结果

从表8中的预测结果来看，未来3年马鞍山市电力需求总量的灰色-马尔科夫预测值均低于GM(1,1)模型的预测结果，同时其增长幅度也低于GM(1,1)模型的预测结果，但是值得注意的是两种预测结果表明未来3年内马鞍山市电力需求总量均保持持续增长态势，且增长幅度有逐年增加的趋势，这就需要马鞍山市加强电力相关的基础设施建设，统筹电力资源合理分配与使用，以保证未来该市的电力需求供应，以满足区域经济的持续发展。

3 结论

电力是我国能源消费的主要品种之一，其在国民经济的发展和社会的日常生活中均发挥着重要的作用，同时有着极强的不可替代性。预测电力能源的需求量对促进国民经济的持续发展和社会的稳定和谐具有重要的意义。本文根据GM(1,1)模型和马尔科夫过程理论的不同特征，构建灰色-马尔科夫组合预测模型，克服了GM(1,1)模型在预测波动较大的样本数据时拟合度差、预测精度低的缺陷，同时有效提高了预测模型的拟合度和预测精度。通过马鞍山市的电力需求量进行实例验证，在案例中灰色-马尔科夫预测模型预测平均相对误差为0.0042，比GM(1,1)模型预测结果的0.0124减少了66.13%；灰色-马尔科夫预测模型均方差为0.0287相较于GM(1,1)模型均方差的0.0931减少了69.17%；在均方差检验上，灰色-马尔科夫预测模型小误差概率较GM(1,1)模型也提高了10%。这灰色-马尔科夫预测模型在预测精度分析上都要优于 GM(1,1)模型，马尔科夫对GM(1,1)模型的修正使得预测结果更加精确合理，并在文章最后对马鞍山市未来3年的电力需求量进行了有效预测。