大地电磁二维各向异性反演及其在青藏高原北部的应用

喻国， 肖骑彬， 李满

1 中国地震局地质研究所， 北京 100029 2 中国地震局地质研究所地震动力学国家重点实验室, 北京 100029

0 引言

地球介质的电性特征受裂缝以及矿物的定向排列、含水量、部分熔融等的影响(Wannamaker，2005；Wang et al.，2006；Yoshino et al.，2006；Dai and Karato，2014)，在不同层次上(地壳以及上地幔)都可能表现出各向异性.而分辨以及解释包含各向异性效应的数据也一直以来是大地电磁测深(MT)方法领域的难点，在针对大地电磁实际数据的各向异性研究中，大多数是应用维性工具、正演模拟等定性分析手段去解释各向异性结构(Wannamaker，2005；Martí，2014).在较早的研究中，人们观察到大地电磁阻抗张量非对角元素的相位曲线有时在长周期存在明显的差异，认为这种相位分离现象是地球深部电各向异性的表现，并有研究将MT数据中的相位分离现象与地震学中的横波分离现象进行对比分析(Kurtz et al.，1993；Simpson，2001；Bahr and Simpson，2002；Leibecker et al.，2002；Eaton et al.，2004; Eaton and Jones，2006；Padilha et al.，2006).然而，随着模型研究的深入，Heise等(2006)指出相位分离现象是由电导率的空间差异或梯度分布引起的，这种现象并不能指征电导率是各向同性的或各向异性的本质特征，因而，MT数据的相位分离与地震横波分离是完全不同类别的现象.相位分离的一种特殊现象是低频段的相位超象限现象(Chouteau and Tournerie，2000)，它可以由各向异性感应产生，并被作为各向异性结构可能存在的印迹(Heise and Pous，2003；Kumar and Manglik，2012；Martí，2014；Liddell et al.，2016).但是，相位超象限现象同样也可以通过三维各向同性结构来模拟(Lezaeta and Haak，2003；Weckmann et al.，2003； Ichihara and Mogi，2009； Ichihara et al.，2013；Xiao et al.，2016；邵贵航和肖骑彬，2016).另外，理论模型研究表明，含有本征各向异性体的模型响应可以用较为复杂的各向同性结构(如宏观各向异性结构)进行模拟(Eisel and Haak，1999；Heise and Pous，2001；Martí，2014)，这种等效性主要是因为在相应的探测深度上MT方法分辨率不足而导致的(Weidelt，1999)，这也提供了利用特殊的等效各向同性结构解释各向异性的可能性.但是，这种等效性的存在也会使得我们通过各向同性反演获得的电阻率结构发生明显的扭曲(Miensopust and Jones，2011；Löwer and Junge，2017)，从而对研究区的结构产生误导.此外，各向异性结构并不是都存在等效的各向同性结构，例如，简单的均匀各向异性半空间的响应无法通过构建等效的各向同性结构来获得(Martí，2014).这些研究结果表明，探测各向异性是极其复杂的过程，仅仅依靠资料的定性分析以及正演模拟等手段来判断地下深部的电各向异性结构还存在着较大的争议，而为了寻找更可靠的各向异性模型来合理解释地下可能存在的结构，我们有必要完成相应的反演算法，同时积累和总结实际数据应用中的经验和认识.

大地电磁各向异性正、反演方法的研究最早可追溯到20世纪60年代，接下来直到70年代末期关于各向异性的大地电磁一维正、反演和二维正演也一直是研究热点.Reddy和Rankin(1971)讨论了层状模型中，倾斜各向异性对大地电磁响应的影响；Reddy和Rankin(1975)利用有限元算法最早实现了二维各向异性模型响应的计算；Abramovici(1974)完成了一维任意各向异性的正演算法；Abramovici和Shoham(1977)应用矩阵广义逆的方法完成针对一维垂直各向异性模型的反演.而在80年代至90年代中期关于大地电磁各向异性问题的研究成果发表量明显减少(徐世浙和赵生凯，1985).90年代后期至今，Pek和Vener(1997)利用有限差分法实现了计算二维任意各向异性模型的正演算法；Yin(2003)讨论了大地电磁各向异性反演固有的多解性；Pek和Santos(2006)将标准的一维奥卡姆反演拓展到各向异性情况；Pek等(2011)完成二维任意各向异性反演算法，并研究了不同参数对反演的影响.随着计算机技术的快速革新，关于各向异性的大地电磁正、反演方法再次成为研究热点(杨长福，1997；Martinelli and Osella，1997；Weidelt，1999；Pek and Santos，2002； Li，2002；Li et al.，2003；Li and Pek，2008；杨长福等，2005；Baba et al.，2006；Mandolesi and Jones，2012；Chen and Weckmann，2012；Plotkin，2012；秦林江和杨长福，2012；胡祥云等，2013；霍光谱等，2012，2015；熊彬等，2013；Qin et al.，2013；Yang et al.，2015；Montahaei and Oskooi，2014；Löwer and Junge，2017；Cao et al.，2018；Kong et al.，2018；Liu et al.，2018；Yu et al.，2018；Xiao et al.，2020；喻国等，2019).

然而，虽然基于各向异性介质的大地电磁正演技术已经可以进行复杂的模型计算，但是各向异性反演在实际数据中的应用依然进展缓慢，这其中一个关键因素在于对各向异性参数的恢复上存在很大的局限(Yin，2003；Pek et al.，2011；Chen and Weckmann，2012).Baba等(2006)首先将二维各向异性反演应用在穿过东太平洋南部洋中脊的大地电磁剖面的解释中，算法在Rodi和Mackie(2001)的二维各向同性反演代码的基础上修改完成了针对三个主轴电阻率的垂直各向异性反演.Baba等(2006)在对反演结果的分析中指出，相比于各向同性的反演结果，各向异性反演并没有明显的改善对数据的拟合程度，因此无法单独依靠大地电磁数据分析来确定各向异性模型为最优模型；然而，通过其他地球物理观测资料与大地电磁的各向异性模型之间的相互印证，才表明得到的各向异性模型是可靠的结果.Pek和Santos(2006)将一维各向异性反演得到的模型作为二维结构试错过程中的初始模型.Pek等(2011)也将他们完成的二维各向异性反演代码应用于葡萄牙南部采集的大地电磁数据，他们认为二维各向异性反演结果有可能受到观测数据中存在的非二维效应的影响，但没有对数据作深入探究；其中，反演待解模型参数为三个主轴电阻率、各向异性走向角以及倾斜角，但反演最终模型整体上呈现较强的各向同性.林长佑等(2004)将一维大地电磁垂直各向异性反演用在天祝—永登地区实际资料的定性解释中.杨长福等(2005)开发了二维大地电磁垂直各向异性反演算法(针对三个主轴电阻率)，认为当电导率沿垂向和倾向表现相同的各向异性时，可以分别用TE和TM极化反演结果来代表两个主轴方向电阻率模型.霍光谱等(2012)基于马夸特方法，完成了大地电磁层状任意各向异性的视电阻率和相位反演，并指出需要将数据揭示的电各向同性与各向异性现象区分，否则无法得到准确合理的地层信息，甚至会出现自相矛盾的情况.秦林江和杨长福(2012)应用广义逆矩阵方法完成一维大地电磁各向异性反演算法，指出对实测资料反演时，如果数据是受各向异性影响的，那么必须用各向异性的处理方法才能得到更客观真实的结果.Cao等(2018)应用有限内存拟牛顿方法完成了针对三个主轴电阻率的大地电磁反演算法，但还没在实际中应用，并且目前还没有其他的大地电磁三维各向异性反演算法完成.通过以上国内外大地电磁各向异性反演应用的情况可以知道，大地电磁各向异性反演算法还不完善，一维各向异性反演在实际应用中存在明显的局限性；二维各向异性反演的实例较少；三维反演目前还没有对数据应用的实例.因此，合理全面地认识和理解地下存在的电各向异性结构，需要进一步发展各向异性反演算法和更多地开展在大地电磁实际数据中的应用.

现今基于三维各向同性介质的反演技术近年来发展十分迅速并已经在实际资料解释中广泛应用(Siripunvaraporn et al.，2005a，b；Egbert and Kelbert，2012；Kelbert et al.， 2014).Kelbert等(2014)完成的ModEM程序将反演过程封装成不同功能的单独模块，为MT方法的推广应用创造了条件.本文在已经实现的二维任意各向异性大地电磁正演算法的基础上(Yu et al.，2018)，构建基于各向异性介质的反演目标函数，实现对目标函数值及其梯度的计算.参考ModEM的非线性共轭梯度法(NLCG)反演模块，实现对各向异性介质的二维大地电磁反演，通过理论模型验证反演结果的稳定性.在此基础上，我们对东昆仑—柴达木盆地过渡带一条MT剖面数据进行各向异性反演解释，该剖面所在的测区的地下地震各向异性背景丰富，但还没有相关电各向异性结构的研究.我们结合该地区以往的地震各向异性研究成果以及本文各向异性反演得到的结果来判断深部各向异性结构的存在性，并进一步分析各向异性的成因及其构造意义.

1 正演模拟

在大地电磁方法中，电场E和磁场H满足麦克斯韦方程组，通过基本的数学代数运算可以得到电场矢量方程或磁场矢量方程.在二维各向异性介质中，因为似稳假设的Maxwell方程组无法再解耦成单独的TE或TM模式，因此这里我们采用一般形式的电场矢量方程

方程组具体表达如下：

(1)

(2)

其中，Rz表示沿Z轴旋转的旋转矩阵，Rx表示沿X轴旋转的旋转矩阵，T表示矩阵转置.

在右旋笛卡尔坐标系下，对模型进行矩形网格剖分，采用经典的交错网格格式来定义场的位置(Yee，1966).对方程(1)进行数值离散，得到线性方程组

AE=B，

(3)

其中，A为系数矩阵，B为右端项，E为所有的未知电场.方程(3)采用直接法求解器PARDISO(Schenk and Gärtner，2004；Kuzmin et al.，2013)进行求解.在求得电场值E后，构建插值向量egi和hgi(下标i=x，y)，统一用解向量E计算地表指定点的电场egiE和磁场hgiE(Newman and Alumbaugh，2000).

计算相互垂直的两组初始水平极化条件下的电场E1和E2后，求得大地电磁响应函数，以在某一观测点的阻抗张量元素Zxy为例，

(4)

2 反演理论

大地电磁各向异性反演问题，可以归结为求解以下目标函数的极小值问题(Tikhonov and Arsenin，1977)：

φ=φd+λsφs+λaφa.

(5)

相比较于各向同性反演，构建的目标函数中除了包含数据拟合项和模型粗糙度项外，还引入了各向异性惩罚项(Pain et al.，2003；Pek and Santos，2006；Pek et al.，2011；Chen and Weckmann，2012).

φa=mTKm.

φa=mTKm=∑[(lnρx-lnρy)2+(lnρx-lnρz)2+(lnρy-lnρz)2]

其一般形式为

φa=mTKm=∑[a12(lnρx-lnρy)2+a13(lnρx-lnρz)2+a23(lnρy-lnρz)2]

其中a12，a13和a23为正数.

在ModEM中，引入新的模型向量

使得

(6)

(7)

(8)

(9)

该式表示依次绕Z轴旋转α角和γ角，α和γ表示相同的旋转角，所以可以将走向角α和偏向角γ合并为同一个参数α，如下：

(10)

因此，综合考虑大地电磁各向异性反演的特点，我们在反演中设置待求解的模型参数只包括ρx、ρy、ρz和α.

(6)—(8)式中，计算量主要集中在(8)式中数据对模型的偏导数计算上.这里N是Np(频率点数)、Ns(测点数)和Nr(每个测点的响应函数数量)的乘积.取d包含全部阻抗张量元素(Zxx，Zxy，Zyx，Zyy)，那么(8)式可以展开为

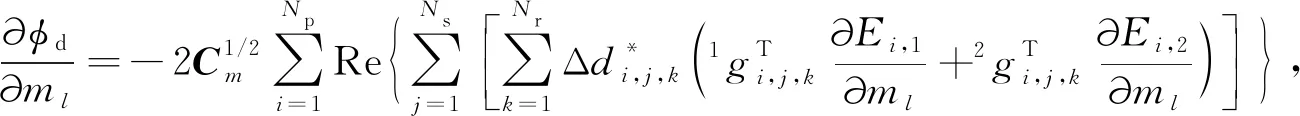
(11)

其中，k代表迭代次数，α为当前搜索步长，p为模型搜索方向.反演计算中实际需要调整的主要参数包括：初始正则化参数λs和λa，正则化参数更新因子k，初始线搜索步长α0，数据误差门槛，以及与模型协方差相关的光滑参数.

在反演迭代的计算过程中，当数据拟合均方根误差(RMS)减小量低于某个阀值时，正则化参数更新为λs/k和λa/k.而初始线搜索步长α0在这里采取人为设定的方式，根据大量反演算例的经验，初始线搜索步长的大小会显著影响反演的收敛过程，当步长过大，模型在初始阶段易发生较大调整而产生冗余构造，在反演后期难以校正，并且这个影响在各向异性反演中更为突出.因此，在实际操作中，我们需要尽量避免在首次迭代中出现很大的模型参数调整.

3 理论模型的反演检验

模型1(Md1)为一包含三个各向异性体的二维模型(图1a).模型背景电阻率为100 Ωm，在8.65 km以上包含两个不同规模的各向异性体A1和A2，它们的顶部埋深都是0.135 km，宽度同为3.2 km.两个异常体之间相距0.8 km，底部埋深分别为8.65 km和1.36 km.两个异常体具有相同的各向异性参数：ρx=1 Ωm、ρy=200 Ωm、ρz=1 Ωm、α=30°、β=0°、γ=0°.异常体A1下伏一个各向异性层，层厚14.42 km，模型参数为ρx=5 Ωm、ρy=50 Ωm、ρz=5 Ωm、α=120°、β=0、γ=0.将该模型在水平方向剖分为46个网格，地表向下剖分为39个网格，地表定义26个观测点，计算周期范围0.015627～15627 s内29个周期点的阻抗响应数据.

如图1b所示，两次反演中拟合RMS偏差相对较大的点是位于异常体A1和A2之间的测点13和14，这表明二维电性结构横向的剧烈变化与各向异性效应一起增加了数据拟合的难度.从模型恢复程度来看(图1c—j)，ρz出现了一些细微的构造，但依然无法实现对异常结构的有效分辨，这主要是因为ρz在二维反演中几乎无法还原，其结构的变化主要是受目标函数中各向异性约束项的影响(Pek et al.，2011).

图1c和d表明，在λs=λa=0.001时，反演恢复A1和A2区域的各向异性参数特点表现为，主轴电阻率ρx为200 Ωm左右的相对高阻ρmax，ρy为1 Ωm左右的相对低阻ρmin，这与真实模型中水平主轴电阻率的分布特点(ρx=1 Ωm表现为低阻ρmin，ρy=200 Ωm表现为高阻ρmax)相反，而在图1f中，A1和A2区域恢复的走向角α约为-60°，与真实的α=30°相差90°.从单独的各向异性参数来看，还原的参数与真实参数不同，但是反演还原的参数组(ρx=ρmax，ρy=ρmin，α=-60°)与真实的参数组(ρx=ρmin，ρy=ρmax，α=30°)代表的是相同的各向异性体，如(12)式所示，两组参数表述的是相同的电导率张量，因此，初始λs=λa=0.001计算的反演结果图1c、d和f基本还原了A1和A2区域真实的各向异性异常体，还原的异常体参数与真实异常参数等效.同样，对图1g、h和j也可以得出相同的结论.

(12)

对于上部异常体A1和A2的尺度恢复，异常中心越集中在浅部越有利于准确地把握异常体的尺度，这也符合大地电磁方法浅部分辨率高的特点(Oldenburg et al.，2013)，走向方位角也能较好恢复异常体的尺度.对于最下方层状异常体，两次反演结果都不能实现对下部异常体的恢复，但是在反演的电性结构中，模型浅部两侧出现了相对异常结构(如图1c中的C1和C2、图1d中的B1和B2).结合测点RMS拟合偏差值观察，两侧的测点拟合程度高，因此，两侧的冗余结构是反演的多解性所导致的.

图1 二维各向异性理论模型及其反演结果(a)二维理论模型Md1示意图及其视电阻率和相位响应拟断面图；图中小倒三角表示地表观测点位置，A1、A2、A3表示各向异性体.(b)取不同正则化参数反演得到的各测点RMS值.红色实点表示λs=0.001和λa=0.001时的拟合RMS值；蓝色空心点表示λs=0.1和λa=0.1时的拟合RMS值.(c)—(f)当取正则化参数λs=0.001和λa=0.001时反演得到的模型与理论模型对比，黑框为理论模型中异常体的范围；(c)—(f)依次为模型参数ρx、ρy、ρz和α的剖面图.(g)—(j)当取正则化参数λs=0.1和λa=0.1时反演得到的模型与理论模型对比.Fig.1 Results obtained by two-dimensional anisotropic inversion of simulated data generated from Md1(a) Complete parameters of Md1 and apparent resistivity and phase response pseudosection generated by Md1. The inverted triangles denote the observation locations; A1, A2 and A3 represent anisotropic anomalies. (b) Comparison of RMS value at each observation point under different regularization parameter sets. The red solid points denote the misfit RMS values with λs=0.001 and λa=0.001. The blue empty circles denote the misfit RMS values with λs=0.1 and λa=0.1. (c)—(f) Comparison of final inverted and true models of anisotropic parameter, ρx, ρy, ρz and α, respectively. The regularization parameters are set as λs=0.001 and λa=0.001. The black boxes show anomalous zones. (g)—(j) Comparison of final inverted and true models of anisotropic parameter, ρx, ρy, ρz and α, respectively. The regularization parameters are set as λs=0.1 and λa=0.1.

图2 不同正则化参数组合下对应数据拟合RMS值的变化Fig.2 The RMS values calculated by different regularization parameter combinations

4 东昆仑—柴达木过渡带岩石圈电各向异性研究

4.1 研究区域各向异性背景

东昆仑—柴达木过渡带东西跨度约1000 km，横亘于青藏高原的北部(图3a).它们之间以柴达木南缘断裂(SQDF)相隔(图3b)，东昆仑造山带大陆地壳主要形成于古元古代晚期，自显生宙以来，东昆仑经历了多期洋陆演化，同时，东昆仑造山带也是一条巨型构造岩浆岩带(莫宣学等，2007).左行走滑的东昆仑断裂带与东昆仑山相伴而生，它继承了早期缝合带特征，并在新生代重新活动.该断裂带现今的走滑速率在中段约11 mm·a-1，并在印度—亚洲板块汇聚过程中吸收北东向挤压而产生缩短变形，对青藏高原的形成及演化发挥了重要作用(Tapponnier et al.，2001).

在青藏高原中部，观察到的地震各向异性可以通过中下地壳的弱流动层解释(Shapiro et al.，2004)，同时该软弱流动层在电性上也表现出较强的各向异性(Le Pape et al.，2015)，但关于它是否越过东昆仑进入到柴达木盆地之下，这仍存在争议(Zhu and Helmberger，1998；Unsworth et al.，2004；Shi et al.，2009；Karplus et al.，2011；Le Pape et al.，2012；Wei et al.，2014).如图3b，我们先后跨过东昆仑造山带与柴达木盆地之间的过渡带的不同位置采集了5条大地电磁测深剖面的数据，并在前期的研究工作中发现，在剖面L15中祁漫塔格下方的上地幔顶部和下地壳底部存在低阻异常体(图3c中C1和C2异常体)(Xiao et al.，2013，2016，2018).同时，该上地幔顶部低阻异常体对应的地面向南约150 km处的地表存在新生代的火山岩(Jolivet et al.，2003；Wang et al.，2005)，Wang等(2005)认为这是增厚的松潘—甘孜地壳下部发生部分熔融的证据.

在这一地区的地震快波偏振方向显示，从阿尔金断裂带到柴达木盆地，快波偏振方向从与阿尔金断裂带走向平行向近东西向转变，发生了顺时针旋转，而少部分的快波偏振方向与地表山脉结构走向不一致，其中，在祁漫塔格内部的一个测点显示最大左行剪切方向为北东向，与祁漫塔格山脉走向不同(Herquel et al.，1999； Soto et al.，2012)，这也为青藏高原北部的动力学过程提供了新的认识.Le Pape等(2012)在重新获取大地电磁剖面的各向异性模型时，发现各向异性的存在使东昆仑与柴达木接触带的地壳结构发生了明显的变化，为松潘—甘孜中下地壳低阻流动层继续向北穿透提供了新的证据.这一节中，我们利用新的大地电磁各向异性反演程序对L15剖面数据进行重新反演，进一步分析在祁漫塔格与柴达木过渡部位低阻通道的各向异性特征，并在下一节的讨论中利用电各向异性参数的变化样式来分析青藏高原北部软物质流的存在及区域应力环境.

4.2 二维各向异性结构

图3 东昆仑—柴达木盆地过渡带和邻区构造背景以及前期大地电磁测点分布图(a)研究区大地构造背景，图中黄色粗箭头表示区域应力方向；ATF：阿尔金断裂带；KLF：东昆仑断裂带；HYF：海原断裂带；RRF：红河断裂带；XXF：鲜水河—小江断裂带；JLF：嘉黎断裂带.(b)东昆仑—柴达木盆地地质图，图中三角形表示大地电磁测深点；其中红色为本次研究的剖面；SQDF：柴达木南缘断裂.(c)沿L15剖面早期二维各向同性反演结果，剖面方向从SW至NE(Xiao et al.，2018).断裂构造参考邓起东等(2003). 地质图据1:250万中国地质图，在线浏览地址: http:∥www.ngac.org.cn/.Fig.3 Tectonic setting of the adjacent area of east Kunlun to Qaidam Basin tranistion zone and distribution of previous MT observation points(a) Tectonic setting of surveying area. The yellow thick arrows denote the direction of the regional stress. ATF: Altyn Tagh Fault; KLF: East Kunlun Fault; HYF: Haiyuan Fault; RRF: Red River Fault; XXF: Xianshuihe-Xiaojiang Fault; JLF: Jiali Fault. (b) East Kunlun-Qaidam Basin geological map. The triangles display MT observation sites, the red ones are the profile we study in this paper. SQDF: South Qaidam Fault. (c) Previous isotropic inversion result along profile L15. The direction of profile is from southwest to northeast (Xiao et al., 2018). The fault structure from Deng et al. (2003). The geology data of 1:2.5 million scale can be browsed at the website: http:∥www.ngac.org.cn/.

反演的模型网格为84×240，84为横向网格剖分，240是地下分层数，模型加入地形的变化，初始模型电阻率为100 Ωm.初始线搜索步长α0=20.

首先，我们进行三组数据分类的各向同性反演：对Zxy和Zyx数据的反演、对单独Zxy分量的反演以及对单独Zyx分量的反演.通过各向异性反演程序实现各向同性反演，只需设定模型参数ρx=ρy=ρz，α=β=γ=0°，这样处理后，目标函数中各向异性惩罚项φa始终为0，不再对反演过程产生作用.然后，选取全部阻抗张量数据(Zxx、Zxy、Zyx、Zyy)，进行反演，待还原的参数仍为ρx、ρy、ρz和α.

从图4a对Zxy和Zyx数据的各向同性反演结果来看，模型的结构特征与Xiao等(2018)中各向同性反演的二维电性结构相似，在剖面最南端的上地幔顶部出现了低阻异常C1，并向北延伸，与柴达木盆地下地壳层次的低阻体C2相连，形成低阻带iso1(图4a)，与图3c中的异常体C1和C2对应(Xiao et al.，2018).然而，这种结构在单独的Zxy分量数据以及单独Zyx分量数据的反演结果中并不明显(图4b和c).

其次，我们在进行阻抗全张量的各向异性反演计算并测试了大量不同正则因子组合后，选择粗糙度正则因子为λs=0.1，其得到的各向异性模型与各向同性模型的结构特征更接近.另外，我们在图4和图5中展示了λa分别选取为0.1、1.0、10.0、100.0、1000.0时，反演得到最终模型和RMS值的对比.图4中，λa=0.1、1.0、10.0、100.0以及1000.0的结果模型对比可以看出，λa在0.1到10.0范围内得到的各向异性结构比较相似，随着λa增大，模型中电各向异性程度降低，当λa达到100.0时，各向异性结构不再明显，在λa=1000.0时，ρx、ρy以及ρz的电阻率结构几乎一致，并且没有明显的各向异性走向角α的结构变化，模型接近于各向同性结构；从图5可以看出，当λa从小到大变化时，最终RMS值在λa=1.0时达到最小，然后呈上升趋势，其中在λa=10.0时，数据拟合最终RMS开始显著增大，对应的目标函数值也明显变大，各向异性惩罚项的目标函数值明显变小.

根据对图4和图5的分析，我们选择RMS值最小即数据拟合最好的结果作为各向异性反演的最终模型(图4h—k)，正则因子组合为λs=0.1和λa=1.0.图6a—d也同为该各向异性模型，ρx和ρy分量的电性结构具有较大的差异，表现出明显的各向异性特征，其中，ρx剖面中的低阻体C1所在位置对应ρy剖面中的相对高阻体R1，C1核心区域各向异性走向角α约为45°；ρx剖面中相对高阻体R2所在位置对应ρy剖面中的低阻体C2，C2核心区域各向异性走向方位角α大约为-45°.这里x轴垂直于测线并指向西北，根据两个异常体的各向异性走向角的旋转效应，两者的低阻电阻率分量C1和C2所在轴的空间方位是在与x轴指向方向夹角45°(顺时针旋转45°)的轴线上，即两个各向异性异常体的最大和最小主轴电阻率的空间展布一致.因此，可以将图6a中C1和R2的位置归为一个各向异性带ani1，它的模型参数可以表示为ρx～3 Ωm，ρy～300 Ωm，α～45°.因为前文提到，已经将观测系统逆时针旋转55°至测线方向，那么再将观测系统顺时针旋转55°至正南北-正东西坐标系统，就可以知道ani1区域里低阻主轴电阻率所在轴的方位呈北偏西10°，如图7所示.

ani1与图4a中iso1的形态接近，前者的整体埋深略浅于后者.另外，在柴达木盆地中心部位的中下地壳，也存在明显的各向异性体ani2(图6a中C3所在区域)，它的模型参数可以表示为ρx～3 Ωm，ρy～500 Ωm，α～ 0°.图6a中ρz分量的电性结构在浅层次有所变化，但变化程度小，这主要也与前文提到的原因相关，即二维反演几乎无法分辨ρz.

在数据拟合RMS方面，二维各向同性反演的总体RMS值要小于各向异性反演的结果，这与各向异性反演中考虑了全部阻抗张量元素有关.如图8a所示，对全阻抗张量各向异性反演的结果(图6a—d)另外计算每个测点对阻抗张量非对角元Zxy和Zyx的RMS，其拟合程度与针对非对角元Zxy和Zyx的各向同性反演(图4a)的RMS拟合程度非常接近，这一定程度说明，各向异性反演过程在对Zxy和Zyx充分拟合的同时，也考虑到了主对角元素Zxx和Zyy的信息.从图8b来看，各向异性反演结果中，对Zxx和Zyy的整体拟合效果不如Zxy和Zyx，但是在测线两端和中间部位，即测点1—3、8—14以及18—27的区间，二者拟合效果相当，而且这三个位置大致与图6a—d中的各向异性结构ani1和ani2的位置对应，因此，Zxx和Zyy的加入有利于反演过程中还原各向异性结构.

为进一步验证各向异性结构的稳健性，我们以图4a中的各向同性结构模型为基础，将该模型大于10.9 km深度的电阻率重新置换为100 Ωm，形成新的初始模型，采用与图6a—d相同的各向异性反演参数设置.在反演开始时，数据拟合RMS为3.5369，明显高于图4a的1.3860.在经过37次迭代后，RMS降为1.7133.反演结果如图6e—h所示，ρx和ρy剖面中还原的ani1和ani2区域的各向异性体与图6a—d同样位置的异常特征基本一致.因此，这个结果说明各向异性带ani1以及ani2能够被观测数据所分辨，并且不能被各向同性体所替代.

图4 剖面L15在不同正则化参数组合下的各向异性反演模型(a)—(c)分别为对阻抗Zxy和Zyx分量、单独的Zxy分量以及单独的Zyx分量的二维各向同性反演结果；(d)—(g)正则化参数组合为λs= 0.1和λa=0.1的各向异性反演结果；(h)—(k)正则化参数组合为λs=0.1和λa=1.0的各向异性反演结果；(l)—(o)正则化参数组合为λs=0.1和λa=10.0的各向异性反演结果；(p)—(s)正则化参数组合为λs=0.1和λa=100.0的各向异性反演结果；(t)—(w)正则化参数组合为λs=0.1和λa=1000.0的各向异性反演结果.Fig.4 The inversion models of profile L15 under different regularization parameter combinations(a)—(c) are the isotropic inversion results from impedance components Zxy and Zyx, component Zxy, and component Zyx; (d)—(g) are the anisotropic inversion results under regularization parameters λs=0.1 and λa=0.1; (h)—(k) are the anisotropic inversion results under regularization parameters λs=0.1 and λa=1.0; (l)—(o) are the anisotropic inversion results under regularization parameters λs=0.1 and λa=10.0; (p)—(s) are the anisotropic inversion results under regularization parameters λs=0.1 and λa=100.0; (t)—(w) are the anisotropic inversion results under regularization parameters λs=0.1 and λa=1000.0.

图5 测线L15在不同各向异性正则化参数下的反演结果统计，其中粗糙度正则因子固定为λs=0.1(a) RMS值； (b) 总目标函数值； (c) 粗糙度项目标函数值； (d) 各向异性约束项目标函数值.Fig.5 The inversion results of profile L15 versus different anisotropic regularization parameters. The roughness regularization parameter is λs=0.1(a) Final RMS values； (b) Full objective function values； (c) Roughness objective function values； (d) Anisotropic objective function values.

5 讨论

(1)Pek等(2011)在二维各向异性反演研究中指出，因为ρz对大地电磁正演响应的影响非常微弱，ρz分量也几乎不能被分辨，在数据中加入倾子等与垂直磁场相关的传输函数也无法改善对这个分量的还原情况，各向异性反演中成像的ρz结构主要受目标函数中各向异性约束项的控制.本文中二维理论模型的反演算例对ρz还原也很不理想，因此，即使我们在实际的反演计算中得到较满意的数据拟合程度，但要进一步还原和解释ρz分量结构还需寻找其他对ρz敏感的地球物理资料或者地质结构信息来支持.

(2)电各向异性是通过电导率张量来表征，而电导率张量可以通过不同的各向异性参数组合来形成，例如，方位各向异性参数组(ρx=10 Ωm，ρy=1000 Ωm，α=-45°)和(ρx=1000 Ωm，ρy=10 Ωm，α=45°)实际上代表的是相同的各向异性结构，这可能会导致在反演中，我们还原出了正确的各向异性结构，但是却由等效的各向异性参数组表述.在对二维理论模型的还原结果中，也出现了这种各向异性参数等效效应.因此，在对各向异性结构进行解释时，要将各向异性参数当作一个整体看待，避免结构认识上的偏差.

(3)在各向异性反演中，浅部冗余结构会压制对深部各向异性体的分辨.在对理论二维各向异性模型的恢复中，可以观察到，随深度增加，对各向异性体的分辨能力逐渐下降，很难得到完整的恢复，同时，浅部会呈现出冗余结构，这种浅层冗余构造同样也是各向同性反演中的难题，它的出现主要是因为反演问题的多解性，而考虑各向异性又显著提升了多解性的程度，因此，通过压制浅部冗余结构来提升分辨深部异常体的能力，是将来各向异性反演中需要深入研究的方向.

(4)对剖面L15的观测数据重新进行大地电磁各向异性反演，发现在祁漫塔格山下方50～100 km的区域存在方位各向异性体ani1.该异常体的水平低阻主轴电阻率空间展布在北偏西10°的轴线上，水平高阻主轴电阻率空间展布在北偏东80°的轴线上.在剖面L15邻近区域已有的远震宽频横波分裂研究结果(Herquel et al.，1995，1999； Soto et al.，2012；Wu et al.，2015)显示，在阿尔金断裂、昆仑山断裂以及柴达木盆地周边，测量的大部分快波偏振方向与主要的地质构造走向相吻合(McNamara et al.，1994；Guilbert et al.，1996).已有实例表明，大多数的快波偏振方向是沿着山脉和其分支走向的(Silver，1996)，而快波偏振方向可以用来指示剪切带方向，这说明大多数深部剪切带与地表构造带可能受到相同变形机制的控制，少数快波偏振方向与地表构造不一致则暗示可能两者受到更复杂的应力环境影响.

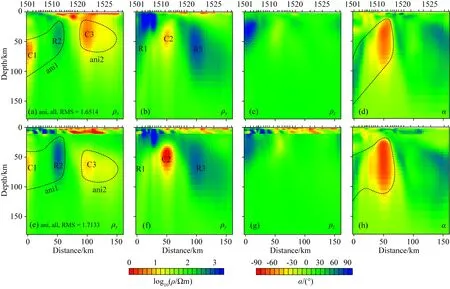
图6 验证剖面L15深部各向异性结构存在性，结果均为利用全部阻抗张量数据对模型参数ρx、ρy、ρz和α进行各向异性反演获得(a)—(d)初始模型为100 Ωm半空间；(e)—(h)初始模型是在图4a模型的基础上，图5a深度10.9 km以上保持不变，将图5a深度10.9 km以下的区域用100 Ωm均匀半空间替代.Fig.6 Examining the deep anisotropic structure of the profile L15. The results are obtained from inverting full impedance elements data for recovering parameter ρx,ρy,ρz and α (a)—(d) The initial model is a 100 Ωm half-space. (e)—(f) The initial model is modified from the model in Fig.4a. The area above 10.9 km depth remains unchanged in Fig.5a. The area below 10.9 km depth of model in Fig.5a is replaced with 100 Ωm half-space.

图7 图6中ani1区域的各向异性异常水平主轴电阻率的空间展布实线表示正南北-正东西的坐标系统；虚线表示沿测线方向的坐标系统，其中y轴是沿测线展布方向；点虚线表示ani1区域各向异性体的水平主轴电阻率ρx和ρy的空间展布，最终低阻主轴电阻ρx在北偏西10°的轴线上.Fig.7 Spatial distribution of the horizontal principal resistivities of the anomaly in the ani1 area of Fig.6The solid lines denote the coordinate axes in west-east and south-north directions; the dotted lines denote the coordinate system of which the y axis is in the direction along the profile; the dot-dashed lines denote the spatial distribution of the horizontal principal resistivity ρx and ρy of the anomaly in ani1 area, the minimum principal resistivity is in the north to west 10° axis.

图8 不同二维反演结果的测点RMS对比(a) 各向同性与各向异性反演结果中次对角元素拟合RMS的对比；三角形：图4a各向同性模型中对Zxy和Zyx计算的RMS值；圆形：图6a—d各向异性模型中对Zxy和Zyx计算的RMS值. (b)图6a—d各向异性反演结果中，对不同阻抗张量元素组合的拟合RMS对比.方形：对Zxy和Zyx计算的RMS值；菱形：对Zxx和Zyy计算的RMS值.Fig.8 Comparison between the data misfit RMS values of different two-dimensional inversion at each site(a) Comparison between the off-diagonal elements data misfit RMS values of isotropic and anisotropic inversion. Triangle shows the RMS value of impedance elements Zxy and Zyx of the model in Fig.4a. Circle shows the RMS value of impedance elements Zxy and Zyx of the model in Figs.6a—d. (b) Comparison between the data misfit RMS values with different combinations of impedance elements of anisotropic model in Figs.6a—d. Square shows the RMS value of impedance elements Zxy and Zyx. Diamond shows the RMS value of impedance elements Zxx and Zyy.

关于地震各向异性与电各向异性间的联系，现在仍然存在争议，当测量的快波偏振方向与电各向异性主轴方向吻合时，有研究认为两者产生于相同的原因(Collins et al.，2006；Frederiksen et al.，2006；Padilha et al.，2006；Carcione et al.，2007；Jones et al.，2009)；而也有一些研究实例认为这两者之间没有明显的关系(Hamilton et al.，2006).地震各向异性与电各向异性之间是否存在关系，这还需在将来通过更多的研究工作去寻找和验证.

剖面L15成像的祁漫塔格山下各向异性体ani1所在位置属于上地幔顶部，Caricchi等(2011)在解释上地幔电各向异性成因时指出，岩石圈下部的部分熔融通道在简单剪切环境下会产生电各向异性.其中，在剪切作用的垂直方向上由于存在应力梯度会降低熔融连通性，产生高阻；而沿剪切方向产生相对高连通性，表现出低阻.

而我们在前期对此次区域的三维各向同性反演研究中(Xiao et al.，2018；Yu et al.，2020)，将剖面L15下的上地幔低阻体解释为熔融的弱物质流，是源自松潘—甘孜下地壳流穿过祁漫塔格山脉向柴达木盆地下方运动的新证据，并且该处邻近区域位于多个剪切带交汇处(阿尔金断裂带，祁漫塔格造山带，昆仑山断裂带等).根据Caricchi等(2011)对地幔电各向异性成因的解释，图6中的各向异性体ani1则可能是该弱物质流运动穿过祁漫塔格山脉下方时与剪切运动相互作用而形成.

这里ani1指示的剪切作用位于北偏西10°的轴线上，该轴线方位与Soto等(2012)在几乎相同位置的地震各向异性结果指示的北偏东45°左右的剪切带方位不一致，这很可能与两种各向异性结构在深度上的变化和跨度不一致相关；另外，ani1指示的剪切作用方位与祁漫塔格山脉走向也不一致，根据这两者间的关系进行推论：深部剪切作用方位与地表造山带地势的不一致暗示，祁漫塔格山脉地下应力环境并不单一，ani1指示的深部剪切作用可能是邻近区域剪切运动的综合体现，祁漫塔格在内的邻近区域深部剪切应力环境可能还受到阿尔金断裂带中部较大的左行走滑运动的影响.

综上，剖面L15反演还原的电各向异性结构与地震各向异性结果指示了不同的剪切作用方位，并且这两种各向异性的空间结构差异较大，所以无法确认两者成因之间的关系；此外，上地幔电各向异性体ani1可能是祁漫塔格山脉下方的弱物质流受到剪切作用的影响而产生的，其表征的深部剪切作用方位与祁漫塔格地表造山带走向不一致则暗示该处应力环境复杂，可能还受邻近阿尔金断裂带左行走滑的影响.

6 结论

基于大地电磁任意各向异性有限差分正演算法以及成熟的NLCG反演模块，本文实现了二维大地电磁各向异性反演，理论模型响应的反演算例也验证了算法的稳定性.

利用该反演程序，我们对穿过东昆仑祁漫塔格山—柴达木盆地的一条大地电磁剖面进行了重新反演.该剖面早期的各向同性结果显示，在祁漫塔格山脉下方的上地幔顶层存在连续的低阻带.在本文中，我们对该剖面进行各向异性反演，并在祁漫塔格下方相同层次的位置发现了明显的各向异性体，其水平低阻主轴电阻率所在轴的方位呈北偏西10°，水平高阻主轴电阻率所在轴的方位呈北偏东80°.我们认为这里的各向异性异常是上地幔弱物质流在祁漫塔格下方受剪切运动的作用而产生沿垂直于剪切作用的方向和沿剪切作用的方向的熔融物质导电性差异而形成的；也暗示这里的应力环境除了印度—欧亚板块碰撞带来的远程挤压效应外，还可能受到邻近阿尔金走滑断裂带左行剪切运动的影响.

致谢感谢Gary Egbert教授提供了ModEM的反演代码.感谢三位匿名审稿人提出的宝贵意见，使本文得以进一步改善.