区块链共识机制中随机性研究

雷元娜, 徐海霞, 李佩丽, 张淑慧

1中国科学院信息工程研究所信息安全国家重点实验室 北京 中国 100093

2中国科学院大学网络空间安全学院 北京 中国 100049

3 齐鲁工业大学(山东省科学院)山东省计算中心(国家超级计算济南中心)山东省计算机网络重点实验室 济南 中国 250000

1 引言

比特币网络[1]的一大亮点是, 解决了如何在大规模动态去中心化系统中保证一致性的问题。因为系统是去中心化的, 所以每个节点都拥有平等的记账权, 为了保证账本的一致性, 潜在的矿工就得通过自身算力来竞争, 算力越高的矿工获取记账权的几率就越高, 最终获得记账权的矿工就称为提案者。比特币网络以这样的方式保证提案者是随机的, 然后其余节点对该提案者提出区块进行验证达成最终的一致性。但这种方式的问题在于效率低, 而且浪费掉了很多的电力资源。为了解决这个问题, 就有人提出基于权益证明的区块链共识机制[2], 这类共识机制不仅可以保证公平性, 还可以在很大程度上减少资源的浪费。基于权益证明的共识机制的主要思想是, 随机选举出一个节点来出块, 被选中的概率和他拥有的股份相关。然后其余的参与者对该区块进行验证最终达成共识。在随机数是不可被操控、不能预测到的情况下, 敌手要实现攻击, 先得成为持币大户, 如果攻击成功币价就会跌落, 那么攻

击者也会承受巨大的损失。而如果随机数能够被敌手预测或者操控, 那么敌手可能对被选中节点发起DOS攻击、节点腐化攻击, 或者增加敌手自己被选中的概率等等。所以如何获取这种既不能被操控到也不能预测到的随机数就成了区块链技术发展的核心问题。

日常生活中, 随机数也有很多的应用场景, 例如抽奖活动、游戏等。因为随机数的广泛应用, 随机数的获取也就成为学术界各个领域研究的热点问题。在理想状态下, 随机数的获取不应该受到任何因素的影响。例如在比特币中, 如果要从比特币的未来某区块的数据来获取随机数, 这样生成的随机数就不能使人信服, 因为这样产生的随机数实际上是由某个个体决定的, 而且也无法证明该个体是否有恶意。

虽然随机数的获取在区块链共识机制中非常重要, 但在区块链中获取随机数是非常困难的。困难性源于两方面: 一方面来自于区块链系统的透明性——即该特性会使得一切算法的公共输入(私有信息除外)、输出以及算法本身暴露给所有的系统参与者——因此, 在密码学中广泛使用的伪随机数发生器就不能以硬编码的方式或者是智能合约代码的方式应用在区块链系统中来获取安全的随机数, 因为系统参与者能够根据代码预测到随机数甚至操纵随机数, 从而让随机数偏向自己的喜好; 另一方面, 随机数获取协议作为区块链系统的一个子协议常常与该系统下的共识协议有着紧密的关系, 这就意味着共识协议的设计有可能会影响到随机数获取协议的安全性。因此随机数获取协议的设计就变得非常复杂, 找不到一个通用的模型来适应所有的区块链协议, 所以就需要对特定的需求进行具体分析。

从上文可以看出, 不可预测、不可操控的随机数获取协议对于区块链发展至关重要。如果采用了一个不安全的随机数获取协议, 恶意的参与者就可能利用这个不安全的协议来破坏区块链的安全性, 例如: 参与者可以停止区块链协议的运行或者破坏区块链去中心化这一性质。因此, 在理解区块链技术安全性的同时, 也要探究随机数在区块链协议中如何发挥作用, 这样才能够更好地利用随机数的特性来推进区块链技术的发展。本文接下来就将探讨随机数在区块链系统中的重要作用。

2 背景知识

2.1 随机数的定义

对于随机数的定义, 我们先从“随机选择”, “伪随机数”, “随机模型”, “随机序列”, 以及 “真随机数”等概念出发。而要理解这些概念, 就需要先搞清楚“随机”是什么。“随机”可以直观上理解为“不确定性”——即我们希望通过一系列操作后得到的结果是我们无法预测到的, 也就是说从某种程度上来讲是无法确定的。因此, 如果直接给出一个数, 但是不给出这个数的产生方式, 就不能称之为随机数。比如直接给出一个数字, 我们不能说这个数字就是随机数, 但如果说这个数字是通过掷骰子来决定的, 则可以说这个数字是随机产生的。不同的学术领域对于“随机数”有不同的定义, 在数学领域, 随机数的定义和概率论相关; 在统计学中, 随机数会根据事件的频率来定义; 在密码学领域, 随机数会结合统计特性和密码攻击来描述。

接下来我们给出随机序列需要满足的性质[3]:

均匀性: 序列服从均匀分布。

独立性: 序列的各个元素相互独立。

不可预测性: 依据序列的任意片段, 不能预测序列余下的部分。

其中均匀性和独立性就是说随机序列生成过程中不可以被操控, 若被操控该序列将不再随机; 不可预测性说的是任何一个人都无法预测到序列下一个元素的值。为了更好地理解随机序列, 我们先举一个简单的例子: 二进制序列。如果说该序列的每一项都为1, 则显然不是一个随机序列, 因为它违反了序列的均匀性, 其中均匀性要求序列中的0和1是均匀分布的。又若它的每一项都和前一项不相等, 这种情况下虽然满足了均匀性, 但仍然不是一个随机序列, 因为这样的序列的元素之间是不互相独立的。对于一个满足独立性和均匀性的序列, 比如从一个常数(如Π, e等)的小数点后的某位置开始依次选取数码来组成的序列。这样的序列虽然满足了随机序列的均匀性和独立性, 但仍然不是一个随机序列, 因为该序列不满足不可预测性。

因为随机数在不同的领域有不同的定义, 所以随机数在这些领域要满足的性质也是不同的, 有些领域要求的随机数性质就比较弱, 即不需要全部满足这三条性质。比如, 在计算机领域的仿真中, 如果想要模拟顾客到达的间隔时间, 只需要满足前两条的随机序列就足够了。但是在密码学领域中, 仅满足前两条的随机序列却是不够的。比如要生成随机的密钥, 一个能被预测的随机序列用在密钥生成过程中就不能够保证密钥的安全性。例如我们用自然对数的底e的数码来作为随机序列, 用在仿真中是足够的, 但是不能用来作密码学中的随机种子。因为敌手

有可能通过一定长度的已知序列猜测到该序列是来自常数e。同样的, 在日常生活中的抽奖、游戏当中使用的随机序列也要求具有不可预测性, 这样才能保证公平性。本文中我们主要关心的是区块链中随机数的获取协议, 又因为区块链技术领域中涉及的多是密码学和游戏的场景, 所以接下来我们用到的随机序列都是满足三条性质的随机序列。

随机序列又可以被分为真随机序列和伪随机序列。伪随机序列, 顾名思义, 就是“不是完全随机, 只是与真随机在某种条件下是不可区分的”。因此, 根据图灵奖得主姚期智提出的概念[3]: 伪随机序列是指一个与真随机序列在计算上不可区分的序列。而真随机序列, 指的是不能够被重现的随机序列, 比如通过抛硬币产生的随机序列。在这样的定义下, 伪随机序列的统计特性和真随机序列应当是无法区分的, 也就是说, 伪随机序列也是满足全部三条性质的随机序列。在密码学当中, 满足三条性质的序列才能称为伪随机序列, 而在其他领域, 只满足前两条性质的随机序列就可以被称作伪随机序列。其中产生随机序列的发生器叫做随机数发生器, 按照产生的序列的性质, 又可以将其分为真随机数发生器和伪随机数发生器。真随机数发生器通常利用一些非确定现象, 通过物理手段将其转换为真随机序列。而伪随机数发生器是一段程序, 是一种确定性的算法, 通常以短的真随机数作为输入, 进行扩充, 生成更长的和真随机序列无法区分的伪随机数序列。

2.2 区块链

自2008年比特币[1]问世以来, 加密货币[4]就开始受到了广泛的关注。在比特币这样的加密货币出现之前, 数字化的货币系统需要可信的第三方机构才能保证交易的安全性和有效性, 而且最终的记账也是由这些可信的第三方机构完成的。而以比特币为代表的加密货币就不需要这样的可信第三方机构, 因为它是去中心化的, 所以系统中的用户地位都是平等的。比特币是一种去中心化的电子现金系统, 在该系统中, 信息公开透明, 每一笔转账都会被全网记录。区块链起源于比特币, 本质上是一个去中心化的分布式数据库。这个数据库不依赖于任何机构, 数据库的数据由全网的节点共同维护, 任何人都可以接入区块链网络, 成为一个数据节点。区块链作为比特币的底层技术, 是一串使用密码学方法产生相关联的数据块, 这些数据块包含了交易的全部信息。

狭义来讲, 区块链是一种按照时间顺序将数据区块以顺序相连的方式组合成的一种链式数据结构, 并以密码学方式保证的、不可篡改和不可伪造的分布式账本。广义来讲, 区块链技术是利用块链式数据结构来验证与存储数据、利用分布式节点共识算法来生成和更新数据、利用密码学的方式保证数据传输和访问的安全、利用由自动化脚本代码组成的智能合约来编程和操作数据的一种全新的分布式基础架构与计算方式。

2.3 本文所用到的密码学工具

要了解区块链系统中的共识协议, 必然离不开密码学, 因为这些协议都是建立在密码学基础之上的, 所以在介绍共识协议之前先简单了解一下协议中用到的三个密码学工具。我们先介绍密码学中的签名方案, 然后再介绍在随机数的获取协议中起到重要作用的两个密码学工具——可验证随机函数和可验证秘密分享。

2.3.1 数字签名方案

数字签名[5]是密码学领域中的密码原语。我们先用一个简单的例子来说明一下数字签名的大概思想:当Alice和Bob双方都希望通过交换消息进行通信时, Alice首先把消息M的数字签名 σ = signskA( M)发给Bob。然后Bob要确保收到的有效签名确实来自Alice。因为Alice是用自己的私钥 Ask来签名的, 所以只有Alice可以生成有效的签名。当Alice把签名后的消息M和签名σ发送给Bob之后, Bob可以让第三方相信Alice确实对该消息进行了有效签名, 并且Alice也不能否认她对该消息的签名。数字签名还可以在签名验证过程中检查被签名的消息M是否被修改过。下面是数字签名的具体算法:

数字签名方案由三个有效的多项式时间算法组成[6]:

(1)密钥生成算法: 该算法是概率算法, 用来创建密钥对(sk, pk), 其中密钥sk为私有, 拥有者用来对消息M进行签名。

(2)签名算法:在给定消息M和私钥sk后, 该算法用来生成对消息的数字签名。因为签名算法可能会用到随机数, 这种情况下该算法就为非确定性算法。

(3)验证算法: 在给定消息M的一个候选数字签名σ和签名者的公钥pk后, 该验证算法检查σ是否是消息M的有效签名,即若 verifypk(σ, M)= 1表示接受, 否则拒绝。

接下来我们给出数字签名方案的一个实例——RSA数字签名方案。该方案最早由Rivest、Shamir和Adleman在文献[7]提出, 具体描述如下:

(1)密钥生成算法:

· 选择两个大的素数p和q

· 计算n = p·q

· 计算 φ ( n) = ( p -1)·( q -1)

· 选择一个整数1 ＜ e ＜ φ(n), 其中e和 φ ( n)是互素的

· 计算 d =e-1(modφ(n)), 为e的乘法逆元

记公钥 pk和私钥 sk分别为 pk = (n,e), sk = (n,d)

(2)签名算法:

使用私钥 sk = (n,d), 签名者通过计算σ≡ Md(modn)得到签名σ

(3)验证算法:

使用公钥 pk = (n,e), 验证者通过计算M "≡ σe(modn)来验证签名的有效性。当且仅当M = M"时, 该验证算法返回VALID。

2.3.2 可验证随机函数(VRF)

可验证随机函数(verifiable random functions, VRF)是由Micali、Rabin和Vadhan等人[8]提出的, 要求生成的数是随机的, 并且要求参与者能够验证该数的生成。也就是说一方面它具有随机性; 另一方面它还具有可验证性, 即它的输出包括一个对函数值正确性的非交互证明, 任何人都可以利用该函数的公钥对这个证明进行验证。我们先给一个简单的描述: Alice让Bob计算某个输入为x的函数 fs, 因为函数的输出结果依赖于只有Bob知道的私钥s, 所以只有Bob才能够正确地计算函数 fs, 其中输出结果v = fs(x)是唯一的, 并且与长度相同的真正随机字符串 v"是计算不可区分的。Bob为了向Alice证明自己确实提供了唯一的正确性结果, B就需要输出一个证明来验证该函数值的正确性。可验证随机函数是由伪随机函数(PRFs)[9]扩展而来的, 所以在具体地介绍可验证随机函数之前, 我们先了解一下伪随机函数。直观上, 伪随机函数就是与随机函数不能区分的函数, 而随机函数可以理解为全体函数集合上的均匀分布的随机变量。由于随机函数描述具有指数长度, 如由{0,1}n到{0,1}函数共有 22n个, 随机函数的描述应不小于2n, 因此, 我们不能用PPT区分算法来说明伪随机函数与随机函数的区分性, 而只能以Oracle访问的方式加以区分。伪随机函数实际上是指定义在函数集合上的随机分布, 每个函数的一般形式为 f :{0,1}k× {0,1}t→ {0,1}l, 其中第一个输入可称为函数的密钥, 对应于密钥空间上的一个分布, 所谓的伪随机性就是当密钥按一定的分布抽样时, 对应的函数集合上的分布与全体函数集合上的均匀分布具有相同的特性(在计算意义上)。伪随机函数和全体函数上的均匀分布以黑盒方式不能被有效区分。因为理想中的随机函数过于复杂, 不可能有效计算。伪随机函数要求可有效计算, 所以其支撑集一定远小于全体函数集合。伪随机函数由复杂性换取了可有效计算性, 因此是在有效性与复杂性(安全性)之间取得平衡。

VRF函数解决了PRF函数的不可验证性问题。考虑这样一种情况:计算 fs(x1), fs( x2),… , fs( xn), 对应的输出为o1, o2,… , on。在不知道s的情况下, 观察者是无法验证 fs(xi)确实对应于相应的输出oi。但若s一旦发布出来, 未来的输出值就不再与真正的随机字符串难以区分了。因为在这种情况下它们是完全可预测的, 任何一方都可以有效地计算它们。为了在不损害未来输出的不可预测性的情况下获得可验证性, 知道种子s的一方需要发布 v=fs(x)和proofx(该证明为零知识证明, 其中 proofx=VRF_Pr oof(s,x))。这个证明可以在不知道种子s的情况下验证v = fs(x)确实成立。另外, 知道种子s的一方只能为每个输入值构造一个唯一的可以验证输出值是有效的非交互式证明。

接下来我们给出可验证随机函数的数学定义: 设G,F,V都是多项式时间算法: G(函数参数生成单元)是概率算法, 以1k为输入, 其中k为安全参数, 输出为(pk,sk); F = (F1, F2)(函数计算单元)是确定性算法, 输入为(sk,x), 输出为 value =F1(sk,x) ,proof = F2( sk,x); V(函数验证单元)是概率算法, 输入为(pk,x,value,proof), 输出为YES或NO。下面给出一个基于双线性映射的VRF函数实例[10]:

(1) G( 1k): 随机选取, 并令sk=s为私钥, pk = gs为公钥;

(2) F = (F1, F2): value =e(g,g )1(x+sk),proof= g1(x+sk);

(3) V: 若 e( gx· pk, proof ) = e(g,g )且value= e(g,proof), 输出1; 否则, 输出0。

假设在双线性群 G(|G|=p)上 (s(k ),2a(k), ε( k ))- DBDHI 成立(l- DBDHI 问题在(G, GT)上定义为: 随机选择, g是G的生成元, 给定一个(l+2)元组, 判定T的值是否为 e(g,g)lα。如果对于任意概率多项式时间算法A在(G, GT)上解决l- DBDHI 问题的优势是可忽略的, 则称l- DBDHI 假设在(G, GT)上是成立的), 则上述(G,F,V)是一可验证随机函数。

2.3.3 秘密共享

秘密共享是由Shamir[10]和Blakley[11]于1979年独立提出的。先非正式的介绍一下秘密共享定义: 一个领导者将秘密分发给一定数量(n)的参与者。这n个参与者中的每一个人都得到了秘密的一部分可以称之为份额(share)。秘密份额分发之后参与者就可以通过相互协作来重构出原始的秘密。成功恢复秘密所需最少的参与者的数量为t, 称之为阈值, 用(t, n)--秘密共享方案来表示。也就是说n个参与者中的任何一组参与者数量为t的(或更多)集合都可以用他们的份额来重构得到秘密。

(1)可验证的秘密分享(VSS)

如上所述, Shamir的秘密共享方案依赖于假设:参与者们都得到了正确的共享份额。然而, 该方案在容错(甚至无信任)分布式系统中是无法使用的, 因为该假设在这种环境下是不成立的[12]。因此, 需要将秘密共享的能力扩展到更广泛的实例中, 所以就有了由Chor、Goldwasser、Micali和Awerbuch等人在1985年提出的新概念——可验证秘密共享(VSS)方案[12]。

在可验证秘密共享方案的验证过程中, 每个参与者都可以验证自己的共享份额是否是由领导者正确创建的。但是在重构过程中, 若存在恶意方参与, VSS方案就不能对秘密提供保护。我们考虑一个Shamir的(t, n) ——秘密共享方案的重构阶段。假设参与者P1, P2,… , Pt-1已经汇集了他们的共享份额。假设参与者tP知道合并后的共享, 那么参与者tP就可以选择一个无效的共享份额来影响重构结果使其成为自己想要的。考虑到在没有比t更多的参与者共享他们的重建份额的情况下, 参与者tP的这种操作是不能被发现的。更糟糕的是, 在重构过程中如果发生纠纷(例如, 不同的t个参与者集合组得到的结果不同), 恶意参与者就可以声称是领导者提供了无效的分享份额。在Shamir的案例中, 出现上述结果是完全合理的, 因为该过程是没有办法证明恶意参与者操纵了重构阶段。

(2)公开可验证的秘密分享(PVSS)

对于可公开验证的秘密共享(PVSS)方案就可以解决我们上面提出的问题。因为这种方案是可公开验证的, 任何第三方(包括参与者)都可以验证参与者提供的共享份额是否有效。这种类型的秘密共享方案因为其良好的性能得到了广泛的应用。我们先简单的介绍一下(t, n) —PVSS方案的一些性质:

1)至少有t份的份额才能计算出秘密S。

2)小于t份份额不能重构出S, 即S的所有可能值都是等概率的[13]。

3)一个恶意的领导者(即发送不正确的份额给一些或所有的参与者)能够被检测到[13]。

4)在重构过程中提供无效份额的恶意参与者也能够被检测到。

5)分配份额和提交重建份额的验证过程是非交互式的[14]。

PVSS方案所特有的性质是:

任何第三方(包括参与者)都可以验证分配的份额以及用于重构的份额的有效性, 即份额的验证过程是公开的。

满足这些性质的PVSS方案有多种不同的类型。首先Stadler提出了一种基于ElGamal的密码系统的PVSS方案[15]。此后, 基于不同的数论假设也提出了多种不同的方案。在Shil等人[16]的文章中我们可以看到对这些方案的概述和比较。本文中我们主要介绍一下由Schonenmaker提出的被广泛应用的PVSS方案[17]。

Schonenmaker的PVSS方案具有的特有性质:

1)标准假设: 该方案仅基于标准假设—DDH假设;

2)简单性: 该方案只提供了一个共享随机秘密的解决方案;

3)低通信成本: 该方案使用最少数量的消息。

下面, 我们就介绍一下该公开可验证秘密分享的实例——Schonenmaker的PVSS方案:

初始化: 领导者先生成并发布方案的参数。然后参与者 ip发布一个公钥 ipk, 并保留对应的私钥 isk。

分配份额: 领导者生成秘密s的共享份额s1,… , sn, 然后用参与者的相应公钥 pki对份额si进行加密, 再将加密后的份额发布。同时发布证据PROOFD证明这些份额确实是有效的加密份额。

验证份额: 在验证阶段, 任何第三方(包括参与者)通过给定的所有公共信息, 进行非交互式验证, 验证值确实是秘密s的共享份额的有效加密。

重构: 该过程如下:

1)解密份额: 这个阶段可以由至少t个参与者的集合来执行。集合中的参与者 ip通过自己的私钥 isk从密文中解密出来对应的份额is, 然后将其公布, 同时公布一个非交互式零知识证明 PROOFi来证明这个值确实是的正确解密。

2)聚合份额: 这个过程也是任意的验证者都可以进行执行的。验证者首先检查假设 PROOFi是否正确, 如果失败则停止。否则验证者就可用至少t份有效份额重构出秘密s。

3 几类主流的基于随机数协议的共识机制

作为本文的主要介绍, 接下来, 我们将提出在分散环境中生成不可操控也不能预测到的随机数的几种方法。在3.1节中, 我们先介绍如何使用承诺方案来获得随机数。然后进一步介绍如何将经济激励与承诺方案结合起来, 并说明由此产生的一些问题。3.2节中描述了在Dfinity区块链系统[18]中如何应用密码学中的签名方案来获取随机数的方法。3.3节介绍了由J. Chen等人[19]提出的Algorand系统中如何巧妙地利用可验证随机函数产生随机数的方法。然后3.4、3.5、3.6节分别介绍了基于PVSS方案产生随机数的几种方法, 即 Ouroboros[20]、RandShare/ RandHound/RandHerd[21]和Scrape[22]。这几个协议中随机数的获取都离不开密码原语——公开可验证秘密分享(PVSS):在Ouroboros中, 协议是在同步模型中运行的。作者为了降低通信成本, 先在时间单元内随机选举出来一个委员会, 然后该委员会中的人员一起执行PVSS方案, 得到最终的可信随机数; 在RandShare中, 在异步模型中, 作者结合秘密分享方案和拜占庭协议来共同生成一个随机数, 为了得到更好的可扩展性, 作者又提出了RandHound和RandHerd两个协议, 协议是将参与者均匀随机地分为几个小组, 然后组内成员共同执行PVSS方案, 从而达到可扩展性并且降低了通信成本; 在Scrape中, 作者先提出了两个基于DDH假设和DBS假设[23]的PVSS方案的变体, 这两个变体在验证阶段使得验证变得更简单, 从而降低通信成本, 然后将这两个变体作为随机数获取协议的子协议, 提出了Scrape协议。关于这几个协议的具体细节我们将在下文中做详细的介绍。

3.1 基本构造

在下面的小节中, 我们首先介绍在区块链系统中获取随机数的一些常见方法。虽然这些方法在特定的场景中非常有用, 但它们不适合作为在分散系统中生成可验证随机性的通用协议。我们将在相应的小节中重点介绍各个问题。

3.1.1 最简单的随机数生成协议

假设Alice 设计了一个抛硬币协议[24]。最简单的情况, 假设只有Alice和Bob两个人参与: 参与者只有一次输入, 输入值是 0或者1。协议的公共输出也是0或者1。从参与者的角度来讲, 这个协议接收自己的输入以及其他节点的输入, 经过协议运行之后, 输出一个一致的结果。该协议就可以作为随机性来源的协议。为了构造这样一个协议, 首先需要确定这样的协议需要满足什么样的性质。因为每个参与者的输入是相互独立的, 所以这样的协议需要保证参与者的输入和输出也是相互独立的, 但是他们又共同对输出做出了一定贡献。只有这样, 才能确保每个参与者都无法只凭借改变自己的输入来改变输出。同时, 协议也需要保证只要有一个参与者的输入是均匀分布的, 那么结果就是均匀分布的。满足这些条件的构造方式有很多, 其中一种是异或操作, 将两人的输入异或之后输出: 在给定Bob选1的情况下(Alice不知道), Alice不管选0还是1, 输出结果都是0和1各一半的可能性; 另一种方法是利用mod加法, 将两人的输入进行模2加法之后输出, 也能得到类似的结果。

3.1.2 带有承诺的随机数生成协议

3.1.1 节看似解决了随机数生成的问题, 实际上它有非常大的不足。这个不足就是无法保证Alice和 Bob “同时” 输入。如果Bob等Alice向协议输入之后再进行输入, 那么由于协议的交互对于两人来讲是公开的, Bob就可以根据Alice的输入来调整自己的输入。这中情况下无论Alice怎么选择, Bob都可以使得异或的结果是自己想要的。因为同时输入是很难保证的, 而为了防止这种作弊行为, 需要保证协议中的其他参与者的输入对于参与者来说应该是暂时机密的, 即不会透露任何他们的输入信息。所以应该多出一个去机密化的过程来计算出协议的输出。为了实现这样的需求, 需要引入新的机制: 承诺(Commitment)。

承诺机制包含两个阶段: 承诺阶段和揭示阶段。在承诺阶段, 协议参与者不再直接输入, 而是对自己的输入先进行承诺, 然后将承诺的结果输入到协议中。当所有参与者的承诺均输入到协议中后, 进入第二个揭示阶段。该阶段所有参与者将第一轮自己的选择输入到协议, 协议会结合第一个阶段的承诺进行验证, 即确认输入的值是否相等。如果所有的验证都通过, 则输出最终结果, 即我们最终想要的随机数。这样的协议可以保证在第一个阶段里没有任何人的输入会被除自己以外的其他参与者获知, 并且在第二阶段, 即使Bob先知道了Alice揭示出来的输入值然后在自己揭示之前计算出结果。因为他在第一个阶段的签名已经对输入值做了“承诺”, 所以他无法改变自己的输入值。

3.1.3 使用经济惩罚的随机数生成协议

3.1.2 节的方案虽然保证了输入的暂时机密性, 但仍有不足, 即: 在有恶意方参与随机数生成的情况下, 协议运行过程中恶意参与者就可以在最后的第二阶段选择是否进行揭示: 在输入自己的选择进行揭示之前先依据别人的揭示结果计算出输出, 如果不是有利的输出, 恶意参与者就可以不进行揭示阶段。上述协议是无法处理这种情况, 所以有两种情况: 重新执行该协议; 取剩下两个人的输入。这两种方法都有问题: 如果重新再运行一遍协议, 那么攻击者就可以利用这种重新运行的机制在每次自己不利的情况下强行使得协议重新运行; 如果只取剩下两个人的输入, 攻击者同样可以利用这种机制选择是否放弃输入来趋利避害。所以我们需要有一种机制来保证参与者不能随意放弃揭示, 最简单的方式就是利用经济惩罚: 当参与者在第一阶段承诺的时候, 必须要向协议锁定一个数字货币, 如果参与者不按时揭示他的输入, 那么就会没收该参与者的数字货币分给剩下的参与者, 然后重启协议。这样的惩罚机制, 就可以防止这样的拒绝服务攻击[25]。

3.1.4 使用门限机制的随机数生成协议

对于上述行为, 除了经济惩罚之外, 还有另外一种方式——门限机制。门限机制指的是一种协议的某一个指标达到一定阈值就可以执行特定流程的机制。在这里引入门限机制, 主要是为了使得在协议参与人数有缺失的情况下仍然能够给出正常的输出。门限机制的作用在于增强协议的健壮性, 使得它能够容忍一定程度的拒绝服务攻击。接下来讨论的门限机制都是(t, n)—门限机制, 即对于n个参与者的协议, 只需要t个参与者的输入就可完成协议的输出。这样的门限机制总的说来有三种。

第一种门限机制是假设在网络同步的情况下, 将输入按照某种规则排序后取前t个输入来生成最终的随机数[26]。它的优点是不需要知道n的确切值。但是该机制不能抵抗女巫攻击(Sybil Attack)[26], 所以这种门限机制是无法用在没有抗女巫攻击机制的环境下。

第二种门限机制是无分发者的秘密分享[27]。这类协议需要每产生一个随机数都进行一次秘密分享来保证门限机制, 属于有状态协议。也就是说有n个人, 只需要t个人提交了就能输出想要的随机数, 同时, 我们需要r个这样的随机数。那么如果采用这种无分发者的秘密分享的门限机制, 就需要n个人相互交互至少r轮。另一个要求是该方案需要在许可环境下才能实施, 也就是说该协议必须知道总人数n, 才能确定出合理的门限t。这类协议包含很多种形式, 其中最基本的形式是无分发者的秘密分享。秘密分享可以将一个秘密字符串分成多个份额(share), 只有集齐一定数量的份额才能将该秘密恢复出来。一般情况下, 秘密分享需要有一个可信第三方充当分发者将秘密分成秘密份额然后分发给参与者。而无分发者的意思是在秘密分享的过程不需要这样的可信第三方, 即去中心化。但是这样的秘密分享方案也是有不足的: 如果秘密分发者在分发共享的时候, 将其中一份份额替换为其他的一个任意值, 那么收到这个份额的节点在使用该份额进行恢复的时候有可能恢复出错误的秘密。为了防止这样的攻击, 需要保证使用的秘密分享方案中包含可以验证秘密分享的步骤。所以我们使用无分发者的公开可验证秘密分享(Publicly Verifiable Secret Sharing, PVSS)—与第一种相比是在分发阶段的时候多了一些额外的数据, 这些数据称之为“证明”。“证明”可以被用来检验每个人收到的份额是否和其他人的一致。所有人都可以使用这个公开的“证明”去验证分发出来的份额, 验证通过就可以说明这个份额确实是和其他发出去的份额是一致的, 也就是说参与者是按照正确的规则生成的。

第三种门限机制是分布式密钥生成[28]+门限签名[29]。门限签名可以理解为秘密分享应用到了数字签名方案中, 但又不是单纯将两者相叠加。通常的数字签名方案是, 参与者用自己的私钥加密了消息获得签名之后, 签名可以被他的公钥等公开参数验证。而该门限机制中使用的门限签名方案里也有一对公私钥, 不同的是每个参与者分别只有总私钥的其中一个份额以及相对应的公钥份额; 这些私/公钥份额集合起来可以恢复出完整的公私钥对; 每个参与者可以利用自己的私钥份额进行签名获得签名份额, 这些签名份额可以被公钥的相应份额验证; 而且这些签名份额中的任意t个合起来就可以计算出一个总签名, 该总签名相当于用总私钥进行签名, 所以也可以被总公钥验证。因此这样的签名过程并不需要所有人参与, 只需要n个人中的t个人的有效签名就可完成签名过程。而且无论是哪t个人参与签名, 最后生成的签名都是一样的。并且签名过程中涉及到的私钥是不会被泄露的, 每个人分享的只有公钥份额和自己的签名结果, 这使得多轮无交互签名成为可能。当然, 这个总的公私钥对以及相应份额不是任意选取的, 它的生成需要所有的n个人在协议第 一次运行时执行分布式密钥生成协议才能生成有这样的密码学特性的公私钥对及其份额。所以这个方案同样存在着协议运行必须要知道总人数n的问题。

探讨了几个一般的随机数生成办法, 以及分析了它们运行时分别存在的弊端。接下来我们介绍目前几种比较主流的共识机制, 然后重点介绍一下在这些共识机制的子协议——随机数获取协议——是如何运行的。

3.2 Dfinity

Dfinity项目[30]是一个由p2p网络节点共同维护的“虚拟区块链电脑”。Dfinity的目标是基于区块链相关的各种技术, 提供一个分散的云平台, 侧重于实现性能、可伸缩性以及容量的改进。而本节要讲的随机数生成协议是Dfinity的共识机制的核心, 它开发了一种在分散环境中生成随机数的方法。

3.2.1 基本模型

我们先基于文献[18]中给出的容错实例来描述Dfinity的模型。Dfinity的假设模型中允许最多有30%的网络节点失败, 通信模型使用的是具有预共享公钥并且经过身份验证的消息。该共识机制中虽然使用了异步BFT协议作为它的一个子协议, 但从全文来看, 整个协议是在同步假设模型下完成的。

3.2.2 唯一门限签名

在介绍随机数获取协议之前, 我们先介绍一下Dfinity共识机制中用到一种密码原语——唯一门限签名。因为前面章节中已经介绍了数字签名方案的一些基本概念, 所以对于门限签名我们只给一些简单的补充。在Dfinity共识机制中用到的签名方案是由Boneh、Lynn和Shacham引入的BLS签名[30]。接下来, 我们先介绍一下BLS签名的两个性质——惟一性和签名聚合能力。

唯一性: 签名方案的唯一性说的是验证算法对每条消息当且仅当只接受一个签名, 这样的数字签名方案就称为唯一签名方案。这样的性质适用于单个签名方案和阈值签名方案中。在阈值签名方案的设置中, 还有一个附加条件: 即签名不能依赖于参与创建签名的子集, 也就是说, 在唯一的阈值签名方案中, 无论由哪个集合来进行签名聚合, 最后得到的群签名都是一致的。

BLS签名作为Dfinity协议中使用的签名方案, 本质上具有唯一性。这里的唯一性是严格强于“确定性”的。唯一性意味着确定性, 但反过来不一定成立, 例如, DSA和ECDSA可以通过重新定义签名函数来确定, 方法是通过一个密码哈希函数从消息加上密钥确定地派生出所谓的“随机k值”, 而不是随机的选择它。但由于无法将k值公开给验证函数, 所以不能使用此技术使DSA或ECDSA具有唯一性。

签名聚合能力: 门限签名方案中签名聚合[32-33]的可能性与前面介绍的秘密共享密切相关。在(t,n)—秘密共享方案中, 领导者将秘密值s的份额分配给n个参与者, 其中至少t个参与者的集合才可以恢复秘密值s。而少于t个参与者的集合将无法获得关于s的任何信息。相比之下, 在(t, n)—门陷签名方案中, 至少由t个成员组成的集合才可以对某个消息M构造出有效的群签名, 而少于t个参与者的集合不能获取关于群签名的任何消息。这样的门限签名方案[34]由以下部分组成:

1)设置:门陷签名方案的设置基本上有两种选择:

a)密钥分发:可信的领导者计算组密钥对, 然后为每个参与者计算一个私有密钥, 并通过安全通道将这些密钥发送给相应的参与者。

b)分布式密钥生成(DKG): 参与者运行一个多方协议来生成他们的私钥和组公钥, 而不需要可信的第三方。在执行DKG协议的时候, 任何一个参与者都不能得到完整的组私钥。

2)签名:参与者计算对特定消息的部分签名, 也称为签名份额。

3)签名聚合:将来自t个参与者的签名份额进行聚合, 来生成对特定消息的群签名。

4)签名验证:任何人都可以使用组公钥来验证聚合签名的正确性。

3.2.3 Dfinity随机信标协议

接下来, 我们介绍Dfinity共识机制如何使用唯一门限签名方案来构造随机信标协议。首先假设网络中的参与者在底层区块链上已经注册了他们的公钥。参与者被随机地分成若干小组, 然后各个组分别运行分布式密钥生成协议(DKG)。如果DKG协议运行成功, 就在区块链上注册该组的组公钥。在分组的过程中, 参与者之间是不能够自由地选择来组成一个组的, 而是通过随机信标协议本身的值然后被分配到特定的组。

1)选取生成随机信标值的组

在块高度为h的情况下, 对于在区块链上注册了公钥的所有组, 要选取其中一个组来生成下一个随机信标值。该组的选取方式如下:

其中, Gh+1代表在块高度h + 1的情况下负责生成随机数的组, σh代表的是在高度h下生成的随机信标值, Gj, j=1,…,m代表已注册的组。

2)生成随机信标值

在给定组 Gh和上一个区块生成的随机信标值σh(通过签名分享的聚合得到的)的情况下, 组里的成员p开始分发签名份额 σhp: 群成员p使用他的私钥对前一个随机数 σh-1进行签名。由于该签名方案具有唯一性, 所以每个签名 σhp都是独一无二的。在收到至少t个成员的签名份额之后, 就可以开始进行签名聚合, 得到最终的群签名。然后我们可以用组公钥来验证该聚合签名的正确性。最终的有效群签名就是该协议获得的随机信标值。

3.3 Algorand

Algorand共识机制是由J. Chen和S. Micali在文献[19]提出的一个公共分布式账本[35]提案。它的目标是解决以前的共识机制的设计中遗留下的的问题, 比如高计算成本(工作证明)[36]或区块链分叉等问题。对于Algorand协议, 文章中作者给出了如下的描述:

Algorand是实现公共分布式账本的一种真正民主和有效的方法。与以前基于工作证明的实现不同, 它只需要很少的计算量, 并且生成的交易历史不会以极高的概率产生分叉[37]。Algorand先介绍了算法的关键概念, 然后重点介绍了两个特别有趣的领域:如何在算法中生成可验证的随机数; 在这样一个随机数生成情况下, 如何将其作为在分散系统中选择领导者和验证者的基本框架。

3.3.1 基础模型

对于Algorand协议中用到的基础模型, 我们根据Chen等人[13]中描述给出关于Algorand的模型的一些关键性假设:

1)拜占庭式的敌手控制着整个系统不到一半的赌注(金钱)。这种假设类似于在比特币或攻击者控制n = 2f + 1个节点中最多f个节点的情况下, 控制最多50%的计算能力。

2)敌手的计算能力是有界的。Algorand协议与其他协议不同的是: 在Algorand中敌手是高度动态的, 也就是说在任何时间点, 敌手都可以立即破坏它喜欢的任何节点, 而唯一的限制是敌手不能控制超过系统一半的赌注。通信模型假设的是所有的消息在一定的时间范围内都可以传递到所有要传递的节点。这个时间限制取决于网络的可达性和消息大小。而网络中消息的完整性和身份验证是由数字签名来保证的。

3.3.2 Algorand随机信标协议

接下来我们介绍该共识机制中是如何获取随机数的。随机数获取协议的核心是领导者和验证者的选择是由不可预测和不可操控的随机数来确定的。本文中是利用VRF函数和数字签名的性质来产生这种随机数的。

在介绍协议之前, 我们先了解一下文中用到的一些基本符号概念:

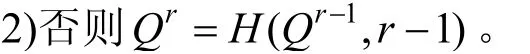
领导凭证: 即证明lr确实是轮r的潜在领导者的证明。这种构造的关键在于签名方案的唯一性。这可以确保(恶意)参与者只有非常有限的选项来影响随机信标的值, 即恶意的领导者只能选择是否泄露SIGlr(Qr-1)来影响生成的随机数。

3.3.3 选举验证者集合

Algorand共识机制是使用拜占庭协议[38]来验证提议的区块。若网络中参与者的数量变大, 那么所有参与者之间都运行这样的协议是不可行的。所以为了避免这个问题, Algorand随机选择一组委员会来执行该验证。尽管验证者的数量远远小于攻击者可能控制的节点数量, 但是为了确保攻击者不能控制超过三分之一的验证者, 委员会的选举必须是随机执行的。在协议中, 验证者的集合是高度动态的, 即在每一轮之后, 甚至在单轮中的各个步骤中, 集合中的参与者都会发生变化。这样的一个动态验证者集合就可以使得Algorand处理一个强大的对手模型[39]。

该集合的选举方式如下: 在第r轮的步骤s中, 参与者i是否为集合中的验证者取决于以下条件:

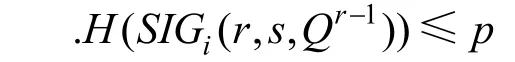
其中, .H(x)表示区间[0,1]中以256位二进制数表示的x的哈希值。其中 Qr-1是上一轮随机信标的值, p是被选中的参与者的概率。

上述方法的一个重要特性是: 其他参与者(包括攻击者)不知道在特定轮中哪些节点是验证者。只有参与者i本身通过计算 SIGi(·)来确定自己是否在验证者集合中。然后参与者i通过发布验证者凭证SIGi(r,s, Qr-1)来说服其他参与者自己确实是验证者。

3.3.4 选举领导者

领导者的选举与验证者的选举非常相似。当.H( S IGi(r,s, Qr-1)) ≤ 1 /n 时, 参与者i就可以称为潜在的领导者, 其中n表示参与者的数量。当然有可能在轮r中没有领导者, 在这种情况下可以通过前一个随机数来自动确定随机信标下一个值。如果有领导者, 但领导者没有做出回应, 这种情况下随机数的产生过程和没有领导者的一轮生成方法是一样的。

当存在潜在的领导时, .H( SIGi(r,s, Qr-1))的最小值对应的参与者即为本轮的领导者。所有潜在的领导者都要完成以下任务:

1)提出一个新的区块(该区块最终被添加到区块链中)。

2)对随机信标的前一个值进行签名, 然后得到下一个随机信标值。

3)发表领导证明, 即 SIGi(r ,1, Qr-1)。

由于该协议[40]不确保只有一个潜在的领导者, 所以在有多个区块提出的情况下, 验证者就需要对其中的一个区块达成共识。具体细节可以看原文描述。

前面提到的随机数获取协议分别是基于数字签名和VRF的, 接下来我们介绍几个基于PVSS方案的随机数获取协议。

3.4 Ouroboros

Ouroboros[20]是由Kiayias等人描述的一类基于权益证明的区块链协议, 该协议描述了一种用于生成可验证随机数的多方协议。协议中获得的随机数的主要用途是用来选举下一个区块的合法提案者。我们只关注随机数是如何产生的, 所以我们只描述文章中模拟可信随机信标的过程[41]。Ouroboros协议中模拟可信随机信标的协议是建立在可公开验证秘密共享(PVSS)的基础上的, 前面的章节中我们已经给出了该方案的具体细节。

3.4.1 PVSS基础

(t, n)— PVSS方案允许领导者在n个参与者之间共享信息, 然后这些参与者中任何一个不少于t个参与者的集合都可以重构该共享信息。而对于任何参与者个数少于t的集合都不能获得关于共享秘密的任何信息。其中参数t我们就称之为(t, n) —PVSS方案的阈值。该方案的具体过程为: 领导者先为协议中的每个参与者计算一个消息份额, 然后每个消息份额都使用相应参与者的公钥进行加密, 这样领导者就可以将加密后的份额通过公共通信通道分发给其他参与者。PVSS方案通过使用非交互式零知识证明(NIZK)来确保任何有权访问份额的人(不仅仅是参与者)都可以验证它们的有效性。这里使用的零知识证明是PVSS方案的一个基本属性, 这种情况下就不需要领导者必须是可信的这一要求了, 因为参与者和第三方可以自行验证领导者的行为是否符合协议规则。在重构过程中, 只要汇集至少t个有效份额就可以成功的重构秘密。然后由Schoenmakers提出的PVSS方案对之前的方案进行了优化, 该方案为了防止参与者提交无效的份额, 在验证过程中其他参与者或第三方都可以验证该参与者提交的份额的有效性并检测是否有操控重构的行为。

3.4.2 基础模型

我们先介绍Ouroboros协议用到的威胁和通信模型[42]: 在协议中, 模型假设是敌手控制着系统中不到50%的股份, 这种假设与传统假设类似(在传统假设中, 攻击者最多控制n = 2f + 1个节点中的f个节点)。协议中通信模型是一个同步模型, 该模型中的时间被分割成称为插槽的离散单元, 其中插槽是与底层分布式分类账[20]的块相关联的。参与者是通过这个区块链来进行交换/广播消息, 并且假设广播的消息是被同一插槽中的其他参与者接收。

3.4.3 Ouroboros的随机信标协议

下面, 我们将描述基于文献[20]的Ouroboros协议的子协议——随机信标协议的构造。该协议由n个参与者 {P1, P2,… , Pn}运行, 分为承诺、揭示和恢复三个阶段。协议构造的安全性是建立在一个诚实参与者占大多数的假设之上。

1)承诺阶段

承诺阶段中, 每个参与者为其私有多项式生成随机数, 并为其他参与者计算份额, 然后以领导者的角色执行(t, n–1) —PVSS协议的份额分发过程, 这些份额和零知识正确性证明是通过区块链发布的。其中的门限t可以设置为f + 1, 这可以确保任何(诚实的)大多数都能够在重构阶段重构秘密[43], 但在没有诚实方参与的情况下, 合谋的攻击者是无法重构秘密的。

2)揭示阶段

如果大多数参与者提供了有效的承诺, 那么在一个固定的时间之后, 参与者就可以开始揭示承诺。否则, 协议将停止。因为Schoenmakers提出的PVSS方案是允许在不需要重构的情况下就可以揭示共享秘密, 所以如果参与者是诚实者, 那么它就会以领导者的身份来揭示基于PVSS方案的系数 α0, 其他参与者可以通过验证是否成立来验证其正确性。

3)恢复阶段

在揭示阶段之后, 参与者开始恢复丢失的共享秘密。即对于所有没有公开的有效承诺, 参与者发布其解密的份额以及相应的份额解密证明。一旦大多数参与者完成了这一步骤, 所有有效的承诺的共享秘密就能够被参与者重构出来。

4)聚合共享秘密

协议的三个阶段完成后, 底层区块链[45]就包含了计算随机信标的所有值和验证其正确性所需的所有信息。不失一般性, 设共享秘密集, 其中对于集合中的每个秘密 iS, 都已经在承诺阶段提交了一个有效的PVSS承诺(即份额及其零知识正确性证明)。那么通过聚合该共享秘密集合就可以得到随机信标的下一个随机数。

3.5 RandShare, RandHound and RandHerd

RandShare、RandHound和RandHerd[21]是在分散环境中获得不可操控与不可预测随机数的三种协议。其中作者将RandShare协议描述为一种小规模协议, 而RandHound和RandHerd则是针对大规模参与者进行的设计, 并且考虑了可伸缩性方面的问题。在RandHound协议中, 客户端通过调用一组RandHound服务器来获得一个新的随机信标值; 而RandHerd协议则是在设置阶段中调用一次RandHound协议, 然后在没有客户端与系统交互的情况下提交一组随机信标值流。

3.5.1 基础模型

对于这三个协议, 作者考虑的是一个拜占庭式敌手控制最多f (n=3f+1)个节点的威胁模型。在文章中, 作者采用消息异步传递模型, 其中每个消息最终都能被传递, 并使用经过身份验证的消息通道, 即发送的消息先要经过发送者进行签名, 然后参与者使用发送方的预共享公钥来验证所传入消息的签名的正确性。对于通信模型, RandShare协议采用的是异步模型, 而对于RandHound和RandHerd协议, 文中并没有给出通信模型的相关细节, 但从全文来看, 协议是在同步模型中运行的。

3.5.2 RandShare

在介绍RandHound和RandHerd协议之前, 我们先简述一下作者提到的一种较简单的协议, 称为RandShare。RandShare协议的操作步骤其实和前面讲到的Ouroboros协议的方法有类似之处。

在RandShare协议中, 每个参与者在执行PVSS方案时充当领导者与其他RandShare节点共享一个秘密值。领导者先对自己私有的多项式的系数进行承诺然后公布出去, 再通过私有信道将共享份额发送给每一个参与者。参与者运行拜占庭协议, 通过系数的承诺集合来验证领导者发给自己的份额是否有效, 如果最终有至少f个人投赞成票, 这种情况下就可以恢复出该随机数, 最终恢复出所有有效的随机数, 异或之后得到最终达成共识的随机数。在投票过程中, 为了容忍多达f个拜占庭式节点, 诚实的参与者在决定合并哪些份额之前是不会透露自己的秘密份额, 也不会参与任何重构工作。所以可以将拜占庭协议与共享验证过程结合运行。

在该协议运行过程中, 作者提到了一个概念——屏障点[46], 在屏障点之后, 所运行的协议才能够确保成功完成。其中所谓的屏障点是否达成取决于拜占庭一致协议的结果。如果说参与者就一组个数至少为f + 1的承诺最终达成一致, 就可以说该集合包含至少一个来自诚实方的承诺。由于所有的承诺都是公开的, 或者通过诚实节点的重构恢复出来的, 因此就可以通过组合得到最终的随机数。因为至少有一个共享是来自诚实方, 所以可以形成一个不可预测、不可操控的随机信标值。

3.5.3 RandHound

RandShare在所有参与者之间使用传统的拜占庭式一致协议, 使得通信成本太高, 导致可伸缩性受限, 因此只能在小规模范围内使用。RandHound协议的设计正是为了解决这一问题。在RandHound协议中, 秘密不是在所有服务器之间共享的, 而是在已被定义好的小子集内进行共享, 从而可以大大减少通信和计算成本, 所以参与者的人数就可以扩大。该协议可以称之为客户机/服务器协议, 随机数是通过客户机发起与RandHound服务器的通信需求来获得的。图1展示了RandHound协议的基本设计:

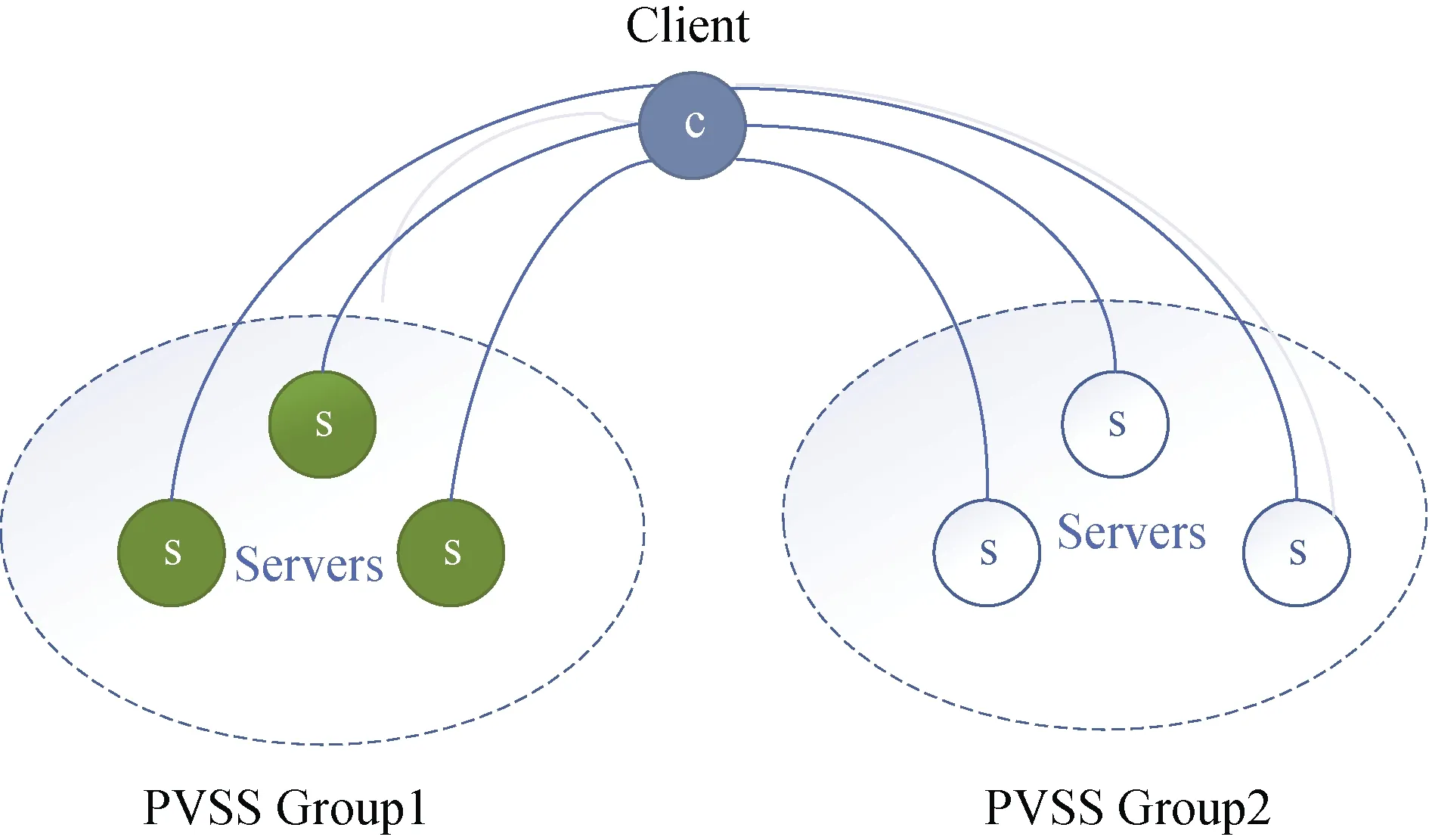
图1 RandHound设计概述 Figure 1 An overview of the RandHound design

然后我们详细地介绍一下RandHound协议获取随机信标值所需的步骤:

1)客户端首先构造一个会话配置, 该配置包含了对随机数预期目标的描述, 并唯一标识协议的运行。此外, 客户机将服务器随机分配到若干组。文章中作者在实现时, 使用了16个组, 然后每个组包含32个服务器。会话配置和组分配结果将被发送给所有的服务器。

2)在接收到会话配置后, 服务器先将其存储起来, 用来检测客户端是否恶意。恶意客户端可能试图多次重新运行协议, 直到收到满意的结果。如果服务器第一次看到配置, 它将执行PVSS协议的共享分发过程, 为组中的其他服务器生成随机秘密的份额。但这些份额并不分发给其他服务器, 而是直接发送回客户机。

3)客户端随机选择使用哪些服务器的随机秘密来获取随机信标的值。对于每个组, 它必须选择该组服务器的三分之一以上。若任何一个组中三分之二的节点都没有响应, 说明它们已经被敌手控制了, 协议就会停止。

4)客户端将上述的选择发送给所有服务器, 然后所有服务器来确认客户机的选择。

5)客户端向所有服务器提供承诺, 服务器验证有效性后使用解密的份额进行响应。

6)客户端恢复出所有选定服务器的随机数。然后客户端组合各个秘密来构造随机信标值。如果无法恢复其中的某个秘密, 则将终止协议。

7)客户端发布随机信标值以及协议运行的记录, 任何第三方都可以进行验证, 然后相信该协议确实获得了最终的随机信标值。

3.5.4 RandHerd

RandHerd协议是Syta等人[21]提出的第三个协议。该协议是针对以固定间隔提供随机信标值序列而设计的。RandHerd协议是基于RandHound协议之上的, 在重复执行的情况下提高了其性能。具体方案描述如下:

RandHerd协议提供了一种持续运行的分散服务, 可以根据需求, 定期或同时生成可公开验证的不可操控、不可预测的随机数。RandHerd协议的目标是在给定组规模大小的情况下, 进一步减少随机数生成的通信和计算成本。在文章给出的描述中, 作者简要地提到了是使用树结构通信和聚合来将服务器的复杂度来降低, 从而减少通信复杂性。

与RandHound协议不同的是, RandHerd协议的运行是不依赖于客户机来发起的。RandHerd协议的实例是由它的配置给出的, 其中配置是由所有服务器的公钥的集合和实例的聚合公钥组成的。RandHound协议是用于该协议的设置阶段, 以此来建立节点到组的安全分片。在成功设置后, 就可以使用基于门陷的目击者协同签名技术[47]的相关协议来获得随机信标值。

3.6 Scrape

在文章[22]中引入的scrape随机信标协议的构造也是基于PVSS方案的。与前面讲的的基于PVSS方案的不同之处在于, 本文的作者是先对Schoenmakers的PVSS方案进行了一个变体[48], 然后基于该构造提出的随机信标协议。因此, 我们主要介绍一下作者的主要贡献:Schoenmakers 的PVSS方案的变体。

与之前提出的PVSS方案的共享验证的计算复杂度为O(nt)指数运算相比, 本文中Schoenmakers方案的变体的计算复杂度为O(n)[49]。对于Ouroboros、scrape和RandShare等基于PVSS的协议同时使用PVSS协议的n个实例, 作者对方案的优化可以实现更好的可伸缩性。Scrape协议中的 PVSS方案的主要思想是: 在方案的秘密共享过程中用相应的Reed Solomon纠错码[50]来对秘密进行编码, 从而降低验证过程中的成本。下面对PVSS方案的优化进行详细介绍:

3.6.1 共享分配

在共享分配过程中, 之前的PVSS方案中, 领导者是使用多项式p(·)的系数 α0,α1, … , αt-1来计算承诺C0, C1,… , Ct-1:

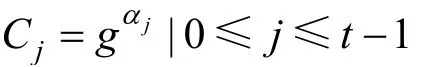
在本文修改后的协议中, 承诺是基于多项式的值来计算的:

因此, 采用了NIZK份额正确性证明, 使用DLEQ子协议 DLEQ(g, Ci,yi,Yi) = c,r1,r2,… , rn来证明加密份额的正确性。

3.6.2 共享验证

之前方案的共享验证依赖于使用 C0, C1,… ,Ct-1来计算 Xi的值:

该计算涉及了O(nt)指数运算, 因此对于大型参与者集来说效率很低。这种计算在修改后的PVSS中是不必要的。因为修改后的方案已经提供了所有 需要的值, 所以可以直接验证NIZK证明[50], 从而使得计算效率得到提高。

在验证NIZK证明之后, 验证者还要执行额外的验证, 来确保承诺是有效的。该验证是通过验证者抽取对应于秘密共享方案实例的对偶码的随机码字样本, 检查与共享向量的内积是否为1[50]。该过程执行的步骤如下:

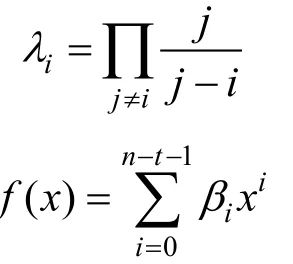
2)计算共享向量 p( 1),p( 2),… , p(n), 检查结果是否为1。只有在以下条件成立时验证才会成功:

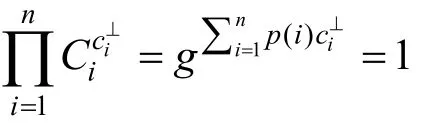
4 总结

在这篇文章中, 我们强调了在分散系统中可公开验证的不可操控、不可预测随机数的重要性。区块链技术的发展离不开共识机制的不断优化和改进的推动, 而随机数作为共识机制的一部分有很大的提升空间。虽然目前存在不少共识机制在设计或者优化思路上比较具有创新性, 但还未能在实际环境中得到有效应用, 也就无法做出准确的性能评估。而现在已经存在于相对较多应用的共识机制当中, 也仍然还有不少值得优化的问题。而随机数的生成是优化共识方案的性能, 安全性, 伸缩性等方面最直接的办法。所以在理解区块链技术的同时, 探究随机数在区块链协议中的角色也非常重要。

综上所述, 区块链技术的共识机制是一个具有很大研究价值的方向。尽管目前已经公布的种类很多, 但是随着区块链技术服务要求的提升和场景的更新, 仍然存在着很多可以优化、创新的方式值得尝试, 还有更加完善的解决方案值得研究。而且也只有通过对共识机制各方面性能的不断完善才能使区块链技术更好地为各个领域的应用服务。对于性能方面, 突破不可能三角问题, 使安全性、一致性、高效性能够得到最好的平衡, 仍然是未来共识机制值的研究的方向; 对于区块链系统中如何降低通信成本, 扩大规模尺寸, 可以从分布式随机数生成算法考虑, 所以随机数的生成也是未来共识机制的研究重点。