基于神经网络的无人机视觉定位方法

关 威，杨紫嫣

(沈阳航空航天大学 自动化学院，沈阳 110136)

目前，无人机在农业植保、森林消防、遥感测绘、军事巡航等领域中担任着重要角色[1]。在无人机的使用中，导航系统是不可缺少的重要组成部分。

无人机定位技术主要依赖于GPS和惯性导航系统。但GPS定位会受到地形、人造建筑物等因素限制，易使系统信号被干扰中断[2-3]。惯性导航系统不依赖于外部信息，但定位误差随时间增大，每次使用之前都需要校准时间。因此，本文研究出一种更加稳定的定位技术，使无人机在外界干扰较强的环境下也能顺利完成任务，为无人机提供所需的位置信息[4-5]。视觉导航定位技术是通过景象匹配算法结合含有地理位置信息的卫星遥感图像实现的。与无人机通过卫星定位相比，具有不受外界电磁干扰、更加稳定等优点。但卫星遥感图像经过处理后具有数据量大和数据类型复杂多样的特点，为了降低工作量，本文在景象匹配的算法基础上，利用神经网络算法对卫星地图识别并分类[6-7]。

目前有许多种景象匹配的算法，如Harris、SIFT、SURF等[8]。SURF算法进行图像匹配时，即使图像间存在平移、旋转等变换都能取得精确的匹配效果。所以本文在利用SURF算法[9]的基础上，结合BP神经网络实现无人机的定位[10-11]。首先建立数据集，利用SURF算法获取无人机图形与瓦片的相似度参数，表示两幅图像相似程度的量化标准。提取无人机拍摄的图片与瓦片的不变矩，分别作为神经网络的输出与输入，建立神经网络模型并进行训练。最后，对本文研究方案进行性能测试，利用测试集进行测试，进入网络中进行粗匹配，再进入SURF算法中精匹配，最后得到无人机具体的经纬度。

1 SURF算法原理

SURF算法是图像特征匹配常用的一种方法，具有尺度不变性，对于旋转、亮度、噪声等有很高的稳定性[12]。在利用SURF算法进行图像匹配时，首先建立图像尺度空间，再在图像尺度空间中寻找极值点，然后构造特征描述向量，最后将求得的特征向量间的距离作为图像相似度的判定依据。在建立数据集时，数据集的输出即为图像经过SURF算法匹配后得到相似度参数，具体步骤如下。

(1)构造金字塔：采用变化的模板盒子尺寸对原图像进行滤波，构造出尺度空间。盒子尺寸滤波模板逐渐增大，并与积分图像卷积，从而产生Hessian矩阵行列式的响应图像，最终构造出金字塔。Hessian矩阵为

其中，Lxx、Lxy、Lyy为高斯滤波后图像g(σ)在各个方向的二阶导数。二阶导数计算方法为：

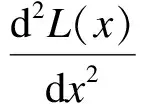
=-2L(x)+L(x+1)+L(x-1)

L(x)=g(h(x))

其中h(x)为原始图像的灰度值，L(x)是将h(x)高斯滤波处理后的图像。

检测关键点：对原图进行变换，在原图中求取每个像素的Hessian矩阵行列式，在变换的图中找到极大值点，即图像中的特征点。Hessian矩阵行列式为：

det(Happrox)=LxxLyy-(0.9Lxy)2。

(2)确定特征点主方向：以特征点为中心，在一定邻域内，统计60度扇形内所有点在水平和垂直方向的Haar小波响应总和，其最大值为该特征点的主方向。

(3)构造特征点描述子：以特征点为中心，将坐标轴旋转到主方向，按照主方向选取边长为20 s(s是所检测到该特征点所在的尺度)的正方形区域。分为16个子区域，在每个子区域统计25个像素相对于主方向的水平方向之和、垂直方向之和、水平方向绝对值之和、垂直方向绝对值之和的Haar小波特征，每一特征点形成64维的描述向量，然后归一化。

当无人机图像与瓦片地图两幅图像的SURF特征向量生成后，采用关键点特征向量的距离作为两幅图像中关键点的相似性度量，即相似度参数。相似度参数代表两幅图的相似程度，值越小代表两幅图匹配程度越高，两幅图的相似度参数作为BP神经网络的输出。

2 基于神经网络和SURF的无人机定位算法

本文提出的无人机定位算法采取粗匹配和精匹配两步策略。首先，利用神经网络模型训练无人机图像与瓦片地图之间的相似关系。通过神经网络对测试数据的判别选取出相似度较高的无人机图像与瓦片；再基于SURF算法对相似度较高的无人机图像与瓦片地图进行精匹配；进而选出与无人机图像匹配最好的瓦片地图；最后，利用瓦片地图坐标与经纬度坐标之间的转换公式，得到无人机的经纬度信息，从而实现对无人机的定位。下面对算法进行详细的描述。

2.1 基于神经网络模型的粗匹配

(1)网络输入。在图像处理中，有许多用来描述物体的特征，Hu矩是用来表示物体的一个重要的特征，且计算简单，具有平移、旋转和尺度不变性，适合于对图像区域特征进行描述[13-15]。因此，本文提取无人机图像与瓦片地图的不变矩作为BP神经网络的输入。因此，可建立样本集I={I1,I2,…,In}。其中I1={x1,x2,…,x7}，xi为无人机图像与瓦片地图不变矩之间的相似性，表1给出了部分样本集。

表1 部分样本数据集

(2)网络输出。网络的输出y为无人机图像与瓦片地图上对应的SURF算法特征点的特征描述子之间的相似性，定义评价指标为：

(3)网络模型的建立。建立一个3层的神经网络模型，如图1所示。

图1 训练模型

网络参数设置如下：

第一步，输入层神经元个数为7，输出层神经元个数为1。建立一个单隐函层的3层BP网络，根据如下经验公式选择隐含层节点数：

式中：n为输入层节点个数；m为输出层节点个数；a为1～10之间的常数。所以建立的网络隐含层神经元个数可设为4、6、8、10等。当a的值为7，隐含层神经元个数为10时，其均方差为0.089，其值最小。因此，确定网络隐含层神经元个数为10。

第二步，创建一个可训练的前馈网络。因基于Levenberg-Marquardt算法的Trainlm函数具有运算速度快，误差小的优点。因此，本文选取Trainlm函数。输入层到隐含层的激活函数为Tansig函数：

隐含层到输出层的激活函数为Purelin函数：gx=x。

第三步，设置BP神经网络的参数，其中，学习率为0.01，训练次数为1 000次，训练目标0.001。

第四步，在建立好的BP网络模型基础上，通过无人机图像与瓦片地图不变矩之间的相似性预测无人机图像与瓦片地图的相似度。

2.2 基于SURF算法的精匹配

本节利用SURF算法提取神经网络预测值较小的无人机图像和瓦片地图的特征点。预测值代表两幅图的相似程度，其值越小，两幅图匹配程度越高。其中特征点的匹配是通过计算两组特征点描述子向量的绝对误差和距离(SAD)实现的。

在神经网络粗匹配后得到无人机图像与瓦片的多组数据，求取一幅无人机图像中的一个特征向量ri与一幅瓦片地图中所有的特征向量si进行匹配，找到最小距离d1与第二小距离d2，d1/d2的值越小相似度越高，当值小于设定阈值0.6时，则判定为匹配成功，结束精匹配过程。

3 实验结果

本文的训练数据建立方法如图1所示，共形成637个训练样本，其中正样本数为349，负样本数为288。本文将在四幅无人机图像U1、U2、U3、U4上验证算法的有效性。无人机图像的分辨率为4 000×3 000。经过5次降采样后分辨率分别为440×330、460×360、490×390、560×420、600×450。进一步提取无人机图像Ui(i=1，2，3，4)的5张不同分辨率的图像与15级谷歌地图50张瓦片的不变矩，并计算它们之间的相似性(本文选用欧氏距离来计算相似性)，最终生成Ui的250个测试数据。

图5 无人机图像U2地理位置

图2-图9给出了与无人机图像U1、U2、U3、U4匹配最优的瓦片及其匹配结果，并在Google地图上标记了无人机当前所在的位置。

图2 无人机图像U1与瓦片匹配结果

图3 无人机图像U1地理位置

图4 无人机图像U2与瓦片匹配结果

图6 无人机图像U3与瓦片匹配结果

图7 无人机图像U3地理位置

图8 无人机图像U4与瓦片匹配结果

图9 无人机图像U4地理位置

从上述实验结果可知，无人机拍摄的图像与瓦片匹配效果较好，通过计算公式(1)、(2)得到无人机的地理位置信息。

(1)

(2)

其中lon、lat分别为经度与纬度，tileX、tileY为瓦片坐标，n为瓦片级别。

表2给出了无人机4个飞行区域所在的经纬度。此实验结果表明，BP神经网络的预测模型具有较高准确性和可靠性。

表2 无人机的地理位置

从匹配时间上看，粗匹配算法在4幅图像上的平均运行时间为0.055 7 s。为了得到更准确的匹配结果，本文针对一幅无人机图像构造了250对样本数据进行精匹配，平均的运行时间为3.21 s。

4 结论

目前大部分无人机的导航都基于卫星导航系统，本文重点针对无人机在无法获取卫星导航信息的情况下，仍能有效导航的问题开展研究。本文基于视觉的无人机定位方法，不依赖于卫星导航信息，仅通过机载摄像头采集地面信息，并通过本文的算法对图像进行处理，便可完成无人机的定位。实验结果表明该算法具有较高的准确性，具备一定的工程应用价值。由于数据集较少，可以引入更丰富的数据源，从而提升模型的泛化性。此方法所消耗的时间不能够满足实时的要求，今后需要进一步探索研究。