无线充电复合补偿网络及其系统充电控制方法

陈祥修，卢闻州

（江南大学 物联网工程学院，江苏 无锡 214122）

0 引 言

现今，电动汽车无线充电系统已成为研究热潮。为满足电动汽车无线充电系统储能装置锂电池的CC/CV充电要求，文献[3]提出运用LCL-LCL型补偿网络和LCL-S型补偿网络分别实现CC和CV充电。两种拓扑以开关的方式组合而成，主要的缺点在于副边所需元器件较多。文献[4]基于SS型补偿网络提出一种T型补偿网络结构，通过在副边级联多个T型网络能够得到具有CC/CV输出特性的补偿网络，再利用开关的方式对补偿网络进行切换，从而实现CC/CV充电。这种方法的缺点在于副边的系统过于庞大，安装在车载上需占用较大空间。文献[5]提出了一种用于S-LCC拓扑的无源组件优化方法，以降低整个系统的成本。利用这种方法不仅能够将无源组件的数量优化到最少，而且仍然能够实现CC/CV充电。文献[6]采用原边负载识别的方法来控制逆变电路，实现了S-S型补偿网络和S-P型补偿网络的CC/CV充电。这种控制方法是通过采集逆变电路输出电流与电压，对硬件与系统参数的准确性要求较高。文献[7]基于LCC补偿网络提出一种负载估计和去耦控制方法，实现原副边系统的独立控制，达到CC/CV充电目的。这种方法的优点在于原副边之间没有数据通信，缺点在于整个系统的控制方法较为复杂，需采样6个交直流电路参数进行计算控制。

为简化无线充电系统的充电控制方法，减少副边无源组件，一种复合补偿网络及其充电控制方法被提出，用于实现CC/CV充电的同时实现其充电效率的优化。全文对复合补偿网络的输出特性进行了理论推导与分析，并提出了相应的控制方法，再由仿真对理论进行了验证，显出系统的CC/CV输出特性及控制方法对传输效率优化的优越性。

1 无线充电系统补偿网络设计

1.1 具有负载无关性的S-S型补偿网络

S-S型补偿网络如图1所示。其中us为原边输入电压，ue为副边输出电压，C1和C2为补偿电容，L1和L2分别为发射线圈和接收线圈的自感，R1和R2分别为发射线圈和接收线圈的等效电阻，M为线圈互感，Zt为副边到原边的等效阻抗，Re为副边输出等效阻抗，i1通过发射线圈的电流，i2为通过接收线圈的电流。

图1 S-S型补偿电路

根据基尔霍夫定理可得：

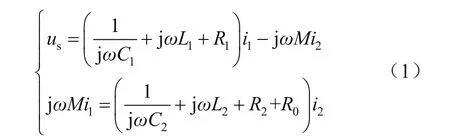
式中，ω为系统谐振角频率。假设电路满足谐振条件jωL1+1/jωC1=0，jωL2+1/jωC1=0，其中ω=2πf为系统工作角频率，f为系统工作频率，进一步得到增益表达式为：

从增益G12的表达式中可以看出，当R1、R2忽略不计的情况下，G12=i2/u2≈j/ωM，i2只与us、M以及ω有关。在系统确定的条件下，这些参数一般不会发生改变，所以i2不会随着Re的变化而变化，这就说明了i2具有负载无关性。

1.2 具有负载无关性的LCL-S型补偿网络

在原来的S-S型补偿网络的基础上加入补偿电感Lt1和Lt2以及补偿电容Ct，得到了如图2所示的LCL-S型补偿电路。

图2 LCL-S型补偿电路

令Z1=jωLt2+jωL1+1/jωC1+R1，Z2=jωL2+1/jωC2+R2，根据LCL-S型补偿网络可以列出基尔霍夫电压方程为：

令Lt1=Lt2=Lt，当电路满足谐振条件jωLt1=jωLt2=-1/jωCt、jωL1+1/jωC1=0 以及 jωL2+1/jωC1=0 时，在忽略发射接收线圈的等效电阻R1、R2的前提下，可以进一步得到以下的增益表达式：

根据增益G11的表达式可以看出，当R1、R2忽略不计的情况下，G11=ue/us≈M/Lt，ue只与us、M以及Lt1、Lt2有关。在系统确定的条件下，这些参数一般不会发生改变，这就说明了ue具有负载无关性。因此，本文利用开关切换的方式将两种补偿网络结合在一个系统中，得到了如图3所示的适用于锂电池充电的复合补偿网路无线充电系统。图3中，Uin为直流电源；Lm为buck电路电感；Cm为Buck电路电容；iL为通过Lm的电流；iout为Buck电路输出电流；Uout为Buck电路输出电压；C3、C4为稳压电容；Req为Boost电路输入等效阻抗；Rb为电池等效负载；U0为Boost电路的输入电压；Ub为Boost电路的输出电压。当开关Q5和Q6闭合，Q7和Q8断开时，锂电池处于CC充电阶段；当Q5和Q6断开，Q7和Q8闭合，锂电池处于CV充电阶段。

图3 复合补偿网络无线充电系统

2 传输效率的优化与充电控制方法的提出

根据式（2）可以得到基于S-S补偿网络的系统电能传输效率表达式为：

同理，根据式（4）可以得到基于LCL-S补偿网络的系统电能传输效率表达式：

从式（5）和式（6）中可以看出，两种补偿网络的系统电能传输效率表达式相同。

令dη/dRe=0即可得到实现传输效率最大化的条件为：

式中，Re-opt为实现最大传输效率所对应的最优阻抗。假设整流环节的损耗可忽略不计，则Boost电路输入电流和输入电压可分别表示为：

式中，I2为i2的有效值，Ue为ue的有效值。另外，还可以得到：

将式（8）代入式（10）化简得：

根据Boost电路特性有：

当Rb发生变化时，可以通过改变α来使Re达到Re-opt，从而使η保持在最大值。

由式（12）可知，当α变化时也会导致负载电流电压发生变化，要使在实现传输效率最大化的基础上，保持充电电流在CC充电阶段保持稳定及在CV充电阶段充电电压稳定，则需要通过调节原边的Buck电路输出电压，进而保证负载电流电压的可调。因此，需要进一步分析D与Ib和Ub之间的关系。

us的有效值Us可以表示为：

由式（2）中的增益G12表达式可知i2的有效值I2=jωMUs/[R1(Re+R2)+(ωM)2]，结合式（8）和式（15）能够得到：

将式（14）和（16）代入式（12）可以得到Ib关于D和α的表达式为：

由式（4）中的增益G11表达式可知ue的有效值Ue=MReUs/[(Re+R2)Lt]，结合式（9）和式（15）能够得到：

将式（14）和式（18）代入式（13）可以得到Ub关于D和α的表达式为：

从式（17）和式（19）可知，通过调节D和α即可让Ib达到参考值Ib-ref，Ub达到参考值Ub-ref。因此，为进一步在CC/CV充电的基础上实现系统电能传输效率的优化，需计算出充电过程中每个Rb对应的最优Buck电路占空比Dopt和αopt。由式（14）变换得α=1-(π2Re/8Rb)1/2，结合式（7）消去Re可得Boost电路占空比α达到最优值αopt的表达式为：

将式（20）代入式（17）和式（19）化简后可分别得到CC充电模式和CV充电模式下，Buck电路占空比D达到最优值Dopt的表达式。CC充电模式下的表达式为：

CV充电模式下的表达式为：

将占空比αopt与Dopt分别赋给Boost电路和Buck电路，系统实现CC/CV充电以及传输效率的优化。

3 仿真验证

为了简化仿真，使仿真结果更加直观，本文将CC充电阶段和CV充电阶段分开进行仿真来验证理论的正确性。仿真参数如表1所示。

表1 仿真参数

图4为CC充电波形，图5为CV充电波形。从图4中可以看出，当Rb由35 Ω增大到50Ω时，Ib能够保持定值。图4中给出了理想条件下（发射接收线圈无R1和R2）的充电电流波形，Ib值更接近充电电流参考值（2 A）。从图5中可以看出，当负载由225 Ω增大到300 Ω时，Ub能够保持定值。图5中给出了理想条件下的充电电压波形，Ub值更接近充电电压参考值（100 V）。

图4 CC充电波形

图5 CV充电电压波形

图6为优化的CC充电波形，图7为优化的CV充电波形。从图6中可以看出，采用上述控制方法能够保持Ib稳定在2 A左右，同样的从图7可以看出Ub能稳定在100 V左右。

图6 优化的CC充电波形

图7 优化的CV充电波形

图8是CC模式优化前后的传输效率对比波形，图9是CV模式优化前后的传输效率对比波形。从图8和图9中可以看出，通过控制优化能够显著提升传输效率。

图8 CC模式优化前后的传输效率对比波形

图9 CV模式优化前后的传输效率对比波形

4 结 论

本文验证了S-S型补偿网络和LCL-S型补偿网络输出的负载无关输出特性，并基于复合补偿网络无线充电系统提出了相应的控制方法，最后实现了系统CC/CV充电以及传输效率的优化。