用于多层油藏层间干扰预测的渗流阻力计算方法

马子麟，师永民，李宜强，管 错，师 翔，李文宏，张忠义，左 静

（1.北京大学地球与空间科学学院，北京 100871；2.中国石油大学（北京）石油工程学院，北京 102249；3.中海油研究总院有限责任公司，北京 100028；4.中国石油长庆油田分公司勘探开发研究院，陕西西安 710018）

多层砂岩油藏在中国广泛分布，储量和产量均约占全国总量的50%［1］。由于层间非均质性的影响，多层油藏注水开发过程中普遍存在层间干扰问题，导致低渗透层不能充分动用，十分不利于采收率的提高［2-5］。因此，层间干扰的表征和分析一直是研究的热点和难点。业界主要采用物理模拟与数值模拟研究层间干扰特征。早期研究常采用采收率表征层间干扰对地层生产状况的最终影响［6-10］；近年来，许多学者在研究中发现，随着开发过程的进行，层间干扰程度是动态改变的［11-14］，但目前仍需通过模拟方法或分层测试表征、预测层间干扰，尚无较为便捷的方法。

耿正玲等研究发现，层间干扰是由水驱油过程中层间渗流阻力差异引起的［15-16］。通过计算层间渗流阻力差异的动态变化，可以预测不同时刻各层吸水量和产液量，分析开采过程中的层间干扰程度，为生产指标的劈分、开发措施的调整提供依据［17-20］。针对油水两相渗流阻力计算，学者们给出了不同形式的求取公式与解法［21-24］，但存在计算复杂或精度不高的问题，不利于推广应用。为此，基于Buckley-Leverett理论，推导了一维水驱油过程渗流阻力计算公式，并通过对油水总流度倒数与含水率导数变化关系的拟合，建立了兼顾精度与效率的两相渗流阻力求取方法。利用单层模型数值模拟，验证该计算方法的准确性，并将该算法应用于多层一维流动层间渗流阻力差异的求取，以期为多层油藏层间干扰的预测以及开发方案调整提供方法和依据。

1 渗流阻力计算方法

1.1 单层渗流阻力计算方法

考虑一维定截面积地层中水驱油过程，模型假设为：①非活塞式驱替，忽略重力和毛管压力的影响，注采平衡。②油、水相流动均服从达西线性渗流定律。③不考虑岩石和流体压缩性。

对于两相区内任一含水饱和度为Sw的截面，通过该截面的瞬时流量可由两相渗流达西定律得到：

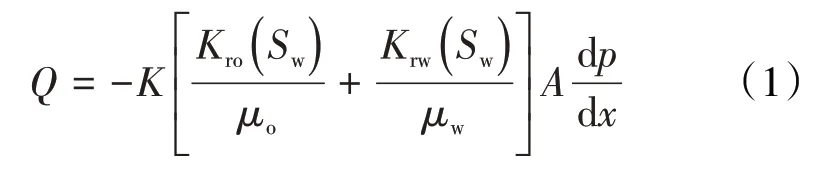
该截面上渗流阻力为：

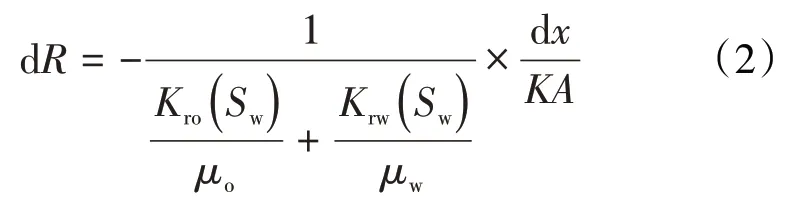
两相区内渗流阻力需由（2）式对两相区长度积分得到：

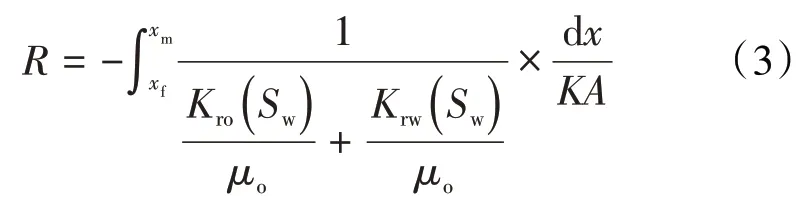
利用Buckley-Leverett 方程（简称B-L 方程），可以将位置转化为含水饱和度。B-L方程给出任一含水饱和度平面的前进距离［25-26］为：

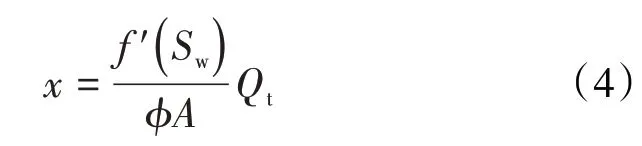
设两相区前缘含水饱和度为f′(Sw)=f′(Swf)，则前缘相对于注入端前进距离为：

（4）式与（5）式相除并整理可得：

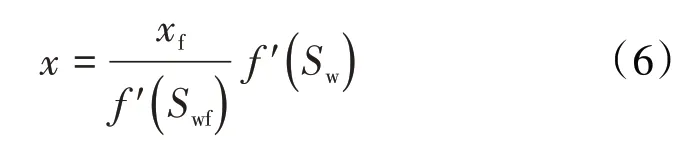
对（6）式微分可得：

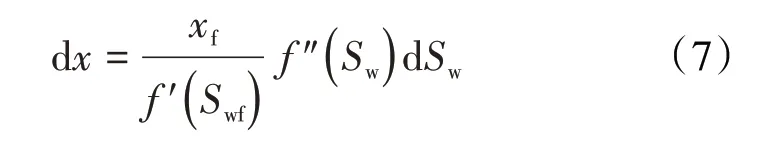
采出端见水前，两相区两端含水饱和度分别为：在x=xf处，Sw=Swf；在x=xm处，Sw=1-Sor。将（7）式代入（3）式并变换积分上下限后，可得两相区内渗流阻力为：

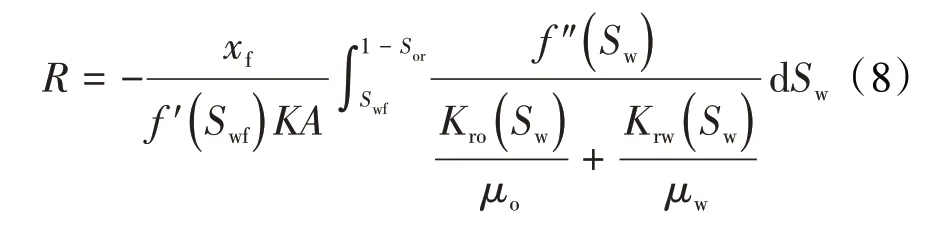
（8）式积分项中的分母部分实际为某一含水饱和度下油水总流度，是某一含水饱和度下地层流体总流动能力的表征，记为：

将（9）式代入（8）式，同时将积分项上下限互换以消去负号，可得：

设从注入端到采出端距离为f′(Sw)=f′(Swf)，在水驱前缘到达采出端前，即xf＜L时，岩心中存在纯油相区与油水两相区，此时总渗流阻力为两区域渗流阻力之和，对其进行整理，可得：

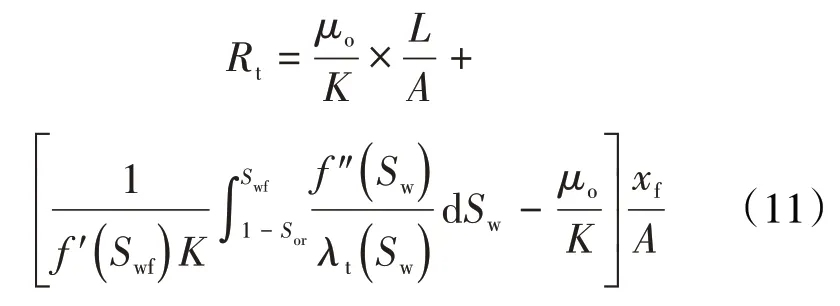
当采出端见水后，为继续分析注采井间油水流动情况，可看作水驱前缘穿过采出端继续向前推进，即将注采井距视为水驱前缘前进距离的一部分（xf≥L）［25-26］。此时注采井间纯油相区消失，两相区渗流阻力即为总渗流阻力；同时前缘含水饱和度平面也消失，因此（11）式中的前缘含水饱和度Swf要相应变为采出端含水饱和度Swe，即：

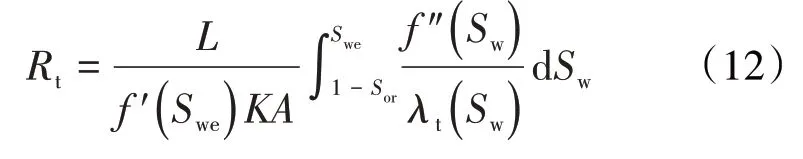
求取总渗流阻力关键在于求出表达式（见水前为（11）式，见水后为（12）式）中的积分项，为便于求解，可将积分项转化为以含水率导数为自变量的形式：

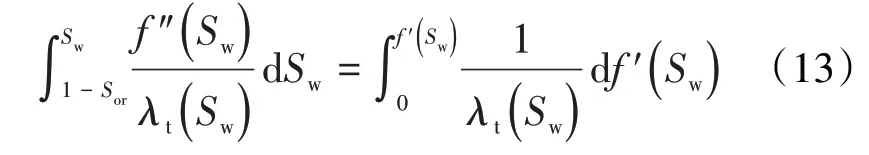
由于油水总流度倒数1/λt(Sw)与含水率导数f′(Sw)之间为隐函数关系，此类积分通常需要采用数值积分［25］或图解法［26-27］得到。其中数值积分方法往往需要专业软件，同时传统的梯形法在数据点之间采用线性插值，可能存在一定误差；图解法则需要人工读图，工作量较大且不易保证结果准确。为此，笔者考虑利用多项式拟合得到两者之间的显式函数关系，即将二者的关系表示为：

（14）式积分得到：

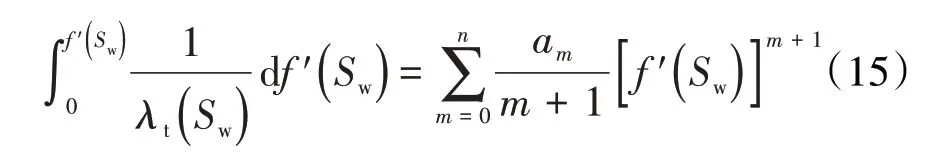
将（15）式分别代入（11）式与（12）式，同时采用矿场单位，渗流阻力最终计算公式可表示为分段函数，即：

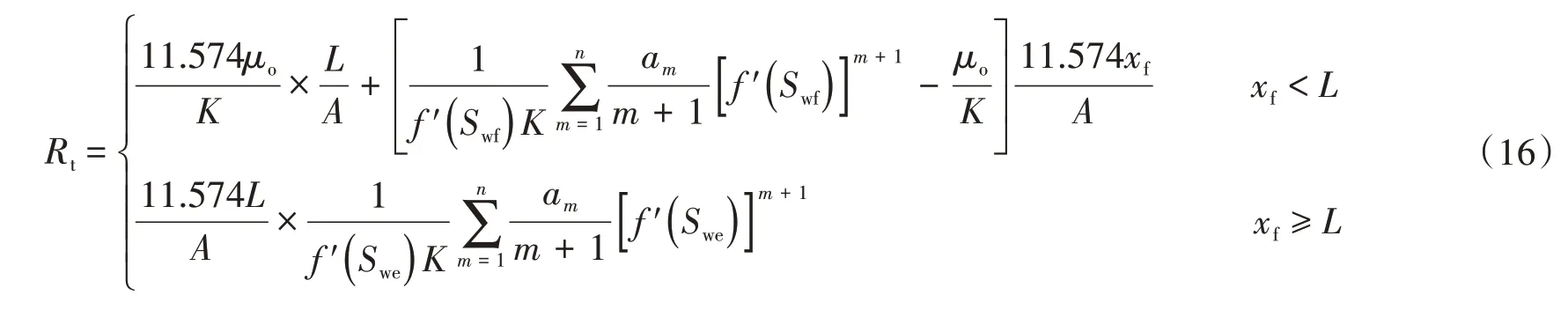
通过多项式拟合得到各拟合系数am值之后，可以由（16）式较为便捷地计算出任意给定含水率导数值对应的渗流阻力值；又由于含水率导数与累积注入量（以注入孔隙体积倍数表示）为倒数关系，最终可得到渗流阻力随累积注入量的变化曲线。

1.2 层间阻力差异计算方法

基于建立的单层渗流阻力计算方法，可计算多层油藏水驱过程中各层渗流阻力变化。假设：①各层间无窜流。②各层流体性质及相对渗透率曲线相同。对（16）式分析可知，任一时刻单层渗流阻力由该层累积注水量确定，而各层的注水量又需由各层渗流阻力的相对大小确定，因此需采用迭代法计算，计算流程如下：①给定储层物性参数渗透率K、孔隙度ϕ、油水黏度μo与μw、注采井距L、截面积A及注水量步长qi。②由（5）式计算前缘位置。③比较xf与L，若xf＜L，由（16）式计算见水前各层渗流阻力Rtik，并根据Rtik值劈分注水量qi+1。④重复步骤②—③至xf≥L。⑤见水后，由f′(Swe)=LϕA/Qt计算此时采出端含水率导数，由（16）式计算见水后各层渗流阻力Rtik，并根据Rtik值劈分注水量qi+1。⑥重复步骤⑤，直至达到设定的注水量上限，计算结束。

2 应用实例

2.1 单层渗流阻力计算与验证

采用某中高渗透岩心的相对渗透率数据进行计算，相对渗透率曲线形态如图1 所示。对应岩心渗透率为200 mD，其余参数设为：注采井距为100 m，地层截面积为1 m2，孔隙度为20%，地层原油黏度为10 mPa·s，注入水黏度为0.5 mPa·s。

图1 油水相对渗透率曲线Fig.1 Oil-water relative permeability curves

首先，根据相对渗透率数据绘制含水率曲线，由切线法［25-27］求出水驱前缘含水饱和度。然后，取其右侧数据点，计算出不同含水饱和度对应的总流度倒数与含水率导数。以含水率导数为横坐标，以总流度倒数为纵坐标，使用多项式对两者在平面直角坐标系内确定的散点进行拟合，得到总流度倒数与含水率导数的关系曲线。所选数据采用三次多项式即可达到较好的拟合效果（图2）。

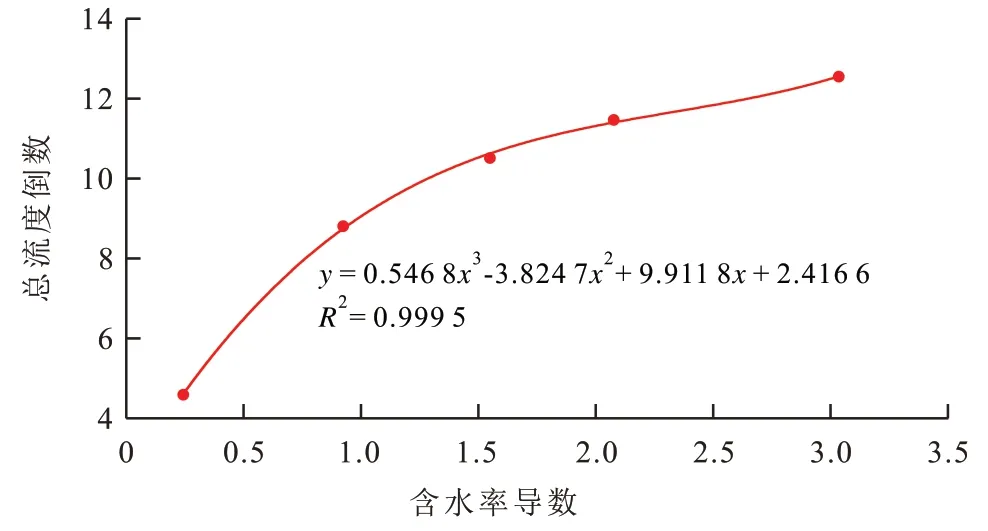
图2 总流度倒数与含水率导数关系曲线Fig.2 Relationship between reciprocal of total mobility and derivative of water cut

给定不同含水率导数，即可求出对应的总流度倒数，进而计算出积分项，得到渗流阻力；同时，根据B-L 方程，可由含水率导数求出对应的注入量，得到渗流阻力随注入量的变化规律。对比本文方法计算结果与数值积分和数值模拟结果（图3）发现：三者计算得到的渗流阻力变化趋势基本一致；但本文方法计算结果与数值模拟结果在渗流阻力大小和变化趋势上均偏差更小，尤其在高-特高含水期。与数值积分方法相比，本文方法简化了计算过程，并且具有更高的精度。本文方法计算结果较数值模拟结果下降略快，一方面可能是由于本文方法计算时忽略了岩石和流体的压缩性，另一方面可能是由于水驱前缘读取及曲线拟合过程中的误差所致；基于B-L 方程计算得到的水驱指标变化快于数值模拟结果，这在其他研究中亦有发现［27］。同时在注水初期，由于数值模拟中能反映出井间压力平衡的过程，使得折算出的渗流阻力在注水初期表现为短暂上升再下降的趋势。但总体来说，本文方法与数值模拟结果较为吻合，相对误差低于12%，说明本文方法能够用于渗流阻力变化的预测与监控。

图3 不同方法计算所得注水过程中渗流阻力变化对比Fig.3 Seepage resistance changes calculated by different methods during water flooding

分析渗流阻力的变化（图3）发现，渗流阻力整体呈现下降最终逐渐减缓的趋势，随着注入量增加，依次分为线性、渐缓和近平缓3个下降阶段。线性下降阶段对应无水采油期，因为由（16）式可知，当水驱前缘未到达采出端时，f′(Sw)=f′(Swf)，渗流阻力实际只是前缘位置xf的函数，而前缘位置又与注入量成正比。当采出端见水后，随着含水率上升，渗流阻力下降速率开始减小，进入渐缓下降阶段，对应中-高含水期。随着含水率进一步上升，进入近平缓下降阶段，渗流阻力下降速率进一步降低，对应特高含水期。渗流阻力的下降速率与含水率的上升速率具有一定对应性，这是由于两者都受到B-L 方程所描述的含水饱和度平面移动速率控制。

2.2 多层非均质油藏渗流阻力计算

以双层介质渗流过程为例，根据计算流程计算水驱过程中各层渗流阻力的变化。同时，引入渗流阻力比值的概念，更加直观地反映层间阻力差异，分析层间干扰程度的变化特征。

2.2.1 注水过程中渗流阻力变化特征

利用本文方法可以计算得到层间干扰程度的动态变化。设两层渗透率分别为200 和100 mD，渗透率级差为2，注采井距为100 m，渗流面积为1 m2，孔隙度为20%，地层原油黏度为10 mPa·s，注入水黏度为0.5 mPa·s。分析计算得到的各层渗流阻力与层间渗流阻力比值（图4）可知，随着注水过程的进行，各层渗流阻力变化趋势相近，但变化速率不同，高渗透层阻力低，下降快，低渗透层阻力高，下降慢。渗流阻力比值反映了两层渗流阻力的差异，表现为一条近抛物线曲线，当注入量为2 PV 时，渗流阻力比值达到最大，由初始值2升高至最大值（约为3.7），层间干扰程度达到最大；当注入量大于2 PV时，渗流阻力比值呈缓慢下降趋势，而此时高渗透层已进入特高含水期，注入水无效循环严重，该层渗流阻力近乎为定值。因此，对多层油藏应及早进行以分层注水为主的调控措施，抑制层间干扰，避免无效注水；而在层间渗流阻力差异达到最大值后，调控措施应以封堵高渗透层为主。

图4 注水过程中各层渗流阻力及渗流阻力比值变化Fig.4 Changes of seepage resistance and the resistance ratio of each layer during water flooding

2.2.2 渗透率级差对层间阻力差异的影响

渗透率级差是层间干扰的主要影响因素［7-9］。控制低渗透层渗透率为100 mD，依次改变高渗透层渗透率为200，300 和400 mD，形成级差为2，3 和4的3 个模型，计算得到渗流阻力比值变化规律。结果（图5）表明，渗透率级差越大，渗流阻力比值越大，层间渗流阻力差异越大。渗透率级差为2时，渗流阻力比值最大值约为3.7；渗透率级差为3 时，渗流阻力比值最大值约为8；渗透率级差为4 时，渗流阻力比值最大值超过12。随着渗透率级差的增加，渗流阻力比值最大值迅速增加，反映层间干扰程度迅速增大，给油藏产油能力带来不利影响。因此，对于多层合注油藏，及早实施调控措施抑制层间干扰至关重要。

图5 不同渗透率级差储层注水过程中渗流阻力比值变化Fig.5 Changes of seepage resistance ratios with different permeability ratios during water flooding in reservoirs

3 结论

基于Buckley-Leverett 理论，推导了兼顾计算效率与精度的一维地层两相渗流阻力计算方法，并通过数值模拟验证了该方法的有效性与实用性。结果表明，本文方法与数值模拟的计算结果在各开发阶段均具有较好的一致性，相对误差低于12%，能够表征水驱油过程中渗流阻力变化规律。

在单层渗流阻力计算的基础上，形成了基于层间阻力差异计算的多层油藏层间干扰程度快速预测方法，并应用该方法分析了中高渗透油藏层间干扰程度随注水开发过程及渗透率级差的变化特征，为多层合注油藏开发措施的调整及调控时机的确定提供了依据。

在计算多层油藏层间阻力差异时假定各层间无窜流，隔层发育较为完善的油藏可以满足这一假设。因此，在应用文中流程进行层间干扰程度预测时，需要加强对隔层发育状况的认识，以确保预测结果的准确性。

符号解释

am——多项式拟合系数；

A——地层截面积，m2；

i——注水量步长序号，i=1，2，3，…；

k——多层油藏层编号，k=1，2，3，…；

K——绝对渗透率，D；

Kro——油相相对渗透率，f；

Krw——水相相对渗透率，f；

L——注采井距，m；

m——多项式中拟合系数对应项的指数，m=0，1，2，3，…，n；

n——拟合得到的多项式最高次项指数，正整数；

p——给定时刻任一含水饱和度平面所在位置压力，MPa；

qi——注水量步长，m3；

Q——两相区内任一截面上的瞬时流量，m3/ks；

Qt——给定时刻累积注入量，m3；

R——两相区内渗流阻力，（mPa·s）/（D·m）或MPa/（m3/d）；

Rt——注采井间总渗流阻力，（mPa·s）/（D·m）或MPa/（m3/d）；

Rtik——第i步第k层总渗流阻力，（mPa·s）/（D·m）或MPa/（m3/d）；

Sw——含水饱和度，f；

Swf——两相区前缘含水饱和度，f；

Sor——残余油饱和度，f；

Swe——采出端含水饱和度，f；

x——给定时刻任一含水饱和度平面所在位置，m；

xf——给定时刻两相区前缘（前缘含水饱和度平面）所在位置，m；

xm——给定时刻两相区末端（最大含水饱和度平面）所在位置，m；

ϕ——地层孔隙度，f；

λt(Sw)——两相区内油水总流度，f；

μo——地层原油黏度，mPa·s；

μw——注入水黏度，mPa·s。