农村饮水安全工程管网优化设计研究

西安黄河规划设计有限公司，陕西 西安 710000

1 供水系统优化

供水系统的优化主要是从系统的规划、设计、运行管理三个方面进行，这也是供水工程的全过程。在规划阶段，应针对管网的布局确定同时满足供水要求和工程经济性的供水规划方案；在设计阶段，要在优化规划方案的基础上，通过建立优化目标函数及其约束条件，确定最优管径组合方案；在运行管理阶段，应采用计算机控制技术，针对使用情况调节水泵和阀门状态，发挥供水系统的最佳性能[1-2]。

文章主要针对设计阶段进行管网的优化，将经济性和可靠性作为目标函数，选择水量和水压及流速的约束条件，建立管网优化设计的数学模型，求解得到管网的管径组合方案[3]。文章构建优化模型的目标函数如下：

1.1 经济性目标函数

经济性目标函数的数学模型如下：

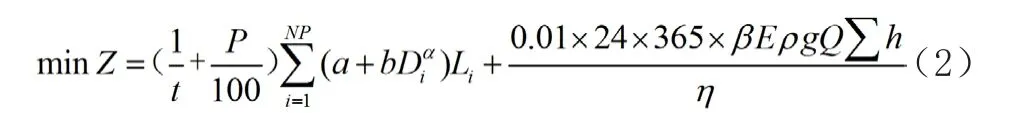
式中：Z为供水系统的工程总造价，是管网的建造和管理费用之和；P为大修折旧费用；t为工程建设投资回收周期；Li和Di分别为管道i的长度和管径；NP为管道总数；a、b、α为常数；β为设计年限内水能量的变化系数；E为电价；ρ为水的密度；g为重力加速度，取9.8；Q为进入管网内的总流量；∑h为供水的起点至最不利节点的总水头损失；η为泵站的效率，取0.6～0.85。

1.2 可靠性目标函数

对于供水管网系统，工程造价和可靠性的关系如图1所示。由图1可知，供水管网的可靠性要求越高，工程的投资就越大，但是其维修和损失费用越低；反之亦然。因此，对于供水管网的建设应该针对实际的工程需要，同时考虑系统的可靠性和经济性，做出最终的设计方案。

图1 可靠性与工程造价关系图

基于以上理论，文章提炼出相应的可靠性公式，具体如下所述。

（1）正常供水情况下，选择节点水压表示管网内的水压。节点富余水头Isi计算公式如下：

正常供水下的可靠性Is计算公式如下：

式中：Hi为节点的自由水头；Hmin为节点要求的最小自由水头；Qi为节点i的流量。

（2）事故情况下，定义事故情况下的管网恢复力Ir计算公式如下：

式中：Pin为克服水头损失所消耗的能量；Pmax,in为标准下允许管网消耗的最大能量；Ir为发生事故后管网的恢复能力。

为了便于分析管网的恢复能力，做出如下假设：

式中：Ptot为输入管网的总能量；Pex为节点处供给用户的能量。

将式（6）带入式（5），可得下式：

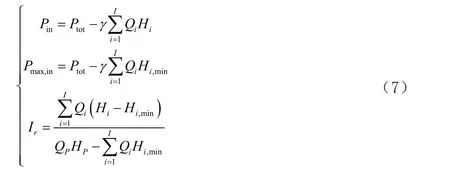
式中：γ为水的比重；QP、HP为泵站的供水量和扬程。Hi,min为节点i最小的自由水头。

1.3 目标函数

根据以上研究，建立考虑供水管网的经济性和可靠性的优化设计多目标函数如下：

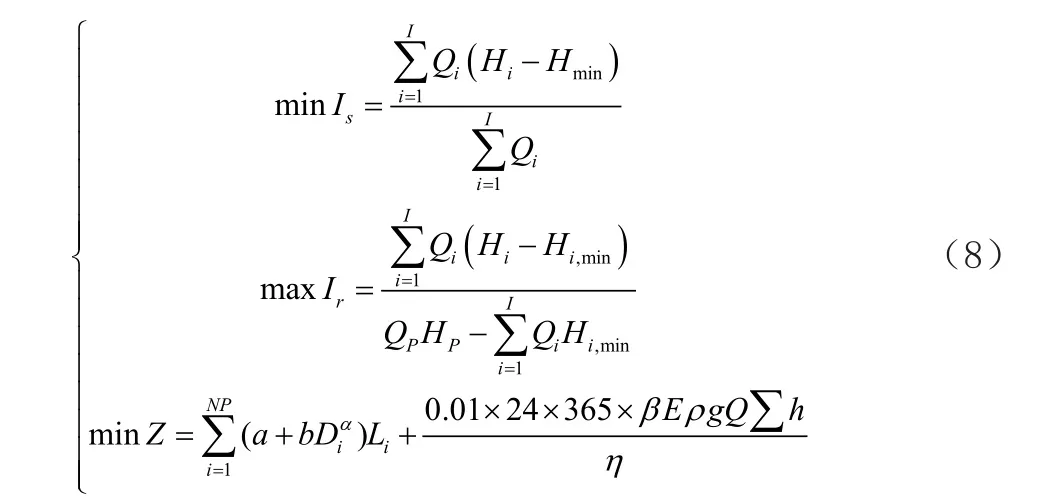
1.4 目标函数的约束条件

在计算时，各个管段的管径和流量均为未知数，为了求解，需要根据环网水流运动规律分别列出节点连续方程、能量平衡方程、段流速限制、节点水压限制、管径约束方程式，如式（9）所示。令供水管网的节点，流出为正，流入为负；供水系统的环状管网中，水流顺时针方向为正，逆时针方向为负。

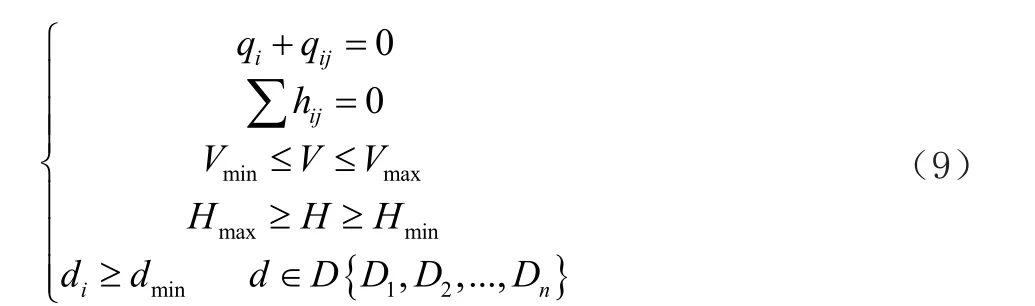
式中：H为节点的水压，Hmax和Hmin为节点i允许的最大和最小水压；dmin为工程所需的最小管径；D为所有管径型号的集合；qi为流入节点i的流量；qij为节点i和j之间管道的流量；hij为节点i和j之间管道的水头损失；V为管道内水的流速。

1.5 多目标函数规划问题的求解

文章选择常用的线性加权和法，根据不同目标的重要程度赋予其不同的权重值，就可将多目标求解的问题转化为求解单一目标的问题，得到最优解。

供水系统的可靠性和经济性的权重值都赋予0.5，可以将式（8）转化为式（10）：

式中：D为供水管网的管道直径。

2 算例分析

该研究选用Excel表格中的“规划求解”功能对供水管网的目标函数进行求解，求解步骤如图2所示。

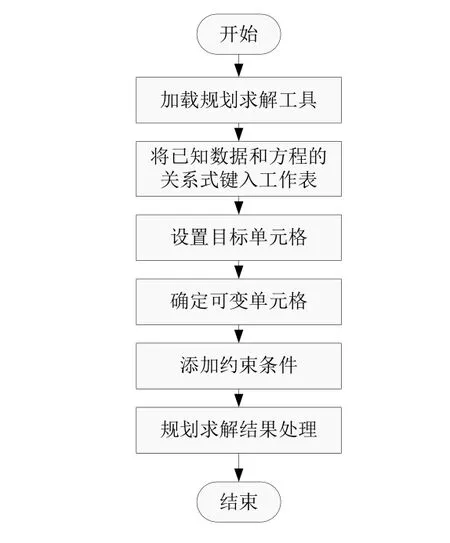
图2 Excel软件“规划求解”步骤

在算例中，管道采用PVC管，管径的型号从100～500共9种型号，节点最小水压为15m，水泵效率为0.75，采用海曾-威廉公式确定管道内的水头损失。在Excel电子表格内输入节点的编号和流量、管道的长度和流量、管径及相应的计算公式，得到管径的优化结果。优化前后的工程费用对比如表1所示。

表1 两种优化方法结果的对比 单位：万元

由表1可知，经过管径优化计算后，总费用节约了25.1万元。优化模型通过构建目标函数，对系统的造价和可靠性都进行了综合的考虑，得到的管网方案更趋近于工程的实际情况，具有较好的实用价值。

3 结束语

文章利用Excel表格对农村饮水安全工程进行了优化设计，得到了较好的设计效果，明显地降低了劳动强度，避免了设计人员的主观影响，提高了工作效率，为相关工程提供了一定的参考。