基于最小二乘法和哈尔小波的随机It-Volterra积分方程的数值解

柯 婷,姜 国,邓梦婷

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

随机积分方程在材料学、生物学、物理学、社会学、经济学、医学等各个领域得到了广泛的应用。然而，大多数随机沃尔泰拉积分方程不能显式求解。因此，研究一种有效的、准确的数值算法具有重要的意义。利用Walsh函数、块脉冲函数、Fourier级数、Legendorian和Chebyshev多项式等正交基函数或多项式来求解不同的Volterra积分方程，见参考文献[1～11].近年来，哈尔小波作为一种强有力的工具，在数值分析中得到了充分的应用。用于求解随机积分方程数值解的文献有[12～14].

在文献[11]中，Maleknejad等人使用模块脉冲函数(BPFs)来求解线性随机It-Volterra积分方程的数值解。Jiang等人利用BPFs研究了二维非线性方程组的数值解[15].Ahmadinia等提出了一种基于最小二乘法和BPFs的计算方法来求解随机It-Volterra积分方程[16].Maleknejad等人利用BPFs和随机积分运算矩阵求解了m维随机It-Volterra积分方程[17].在文献[12]中，Fakhrodin用哈尔小波(HWs)推导了线性随机It-Volterra积分方程的数值解。

与文献[11,16,17]相比，本文最重要的创新是将最小二乘法和哈尔小波相结合，将随机It-Volterra积分方程转化为线性代数方程组。

第一节，给出了模块脉冲函数和哈尔小波函数的一些基本概念。第二节，给出了HWs与BPFs之间的关系。第三节，引入最小二乘法。第四节，证明了误差分析。第五节，利用MATLAB进行了数值模拟。

1 预备知识

1.1 模块脉冲函数

BPFs已经被许多作者研究并应用于解决不同的问题，见文献[3,10,11,15,17].定义BPFs为：

1.2 哈尔小波函数

正交HWs的定义如下[12]：

哈尔小波hi(t)在区间[0,1)是成对标准正交的，

其中δij是Kronecker符号。

满足任何均方可积的函数X(t)可以被HWs近似表示如下形式：

当m=2J(J为小波分辨率等级)，X(t)可以被近似表示为：

向量形式如下：

(2)

其中Hm=(h0(t),h1(t),…,hm-1(t))T是HWs向量，Cm=(c0,c1,…,cm-1(t))T是HWs系数向量。

同理，令S(u,t)∈L2([0,1)×[0,1))，它可以被HWs表示为：

其中S=(sil)m×m

(3)

其中i,l=0,1,…,m-1.

2 HWs和BPFs

本节介绍一些关于HWs和BPFs的引理。

引理1[12]设Hm(t)和Ψm(t)分别是HWs向量和BPFs向量，则Hm(t)可以被近似表示如下形式：

Hm(t)=PΨm(t)m=2J

(4)

其中P=(Pij)m×m，

引理2[12]对于在(4)中给定的矩阵P，则有

引理3[12]设F是m维向量，则有

引理4[12]设G是m×m矩阵，则有

引理5[11,12]对于给定的Ψm(u)，有

其中

引理6[11,12]对于给定的Ψm(u)，有

其中

引理7[11,12]对于在(2)中给定的Hm(t)，有

引理8[11,12]对于(2)中给定的Hm(t)，有

3 数值算法

考虑线性算子L：

(5)

假设X(t)是(1)的精确解，则残差范数消失，

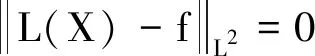
对于给定的ε>0，考虑Xε(t)是(1)的近似解，使Xε(t)的残差范数小于ε，

根据(6)，可以得到一种方法来获取近似解，Xm(t)是一个HWs的线性组合，

其中ci是未知系数，考虑如下最小化问题：

(7)

(8)

其中m→∞(或者h→0)

为了求(7)中近似解的最小值，求解如下线性方程组，

(9)

然后(9)可以被写成，

简化成如下线性系统，

Ac=b

(10)

其中c=(c0，c1，…，cm-1)T∈Rm,b=(b0,b1,…,bm-1)T∈Rm,和A=(aij)∈Rm×m.

bi=〈L(Hi(t)),f(t)〉

aij=〈L(Hi(t)),L(Hj(t))〉,i,j=0,1,…,m-1

(11)

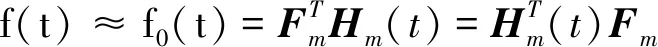
(12)

(13)

(14)

其中Cm,Fm是HWs的系数向量，S1,S2是HWs的系数矩阵。

为了求解方程(10)，我们需要求解aij，bi,从而得到A矩阵和b向量。

根据(5)，(11)-(14)，L(Hi(t))和L(Hj(t))可以用HWs近似地表示，根据引理3、引理4、引理7和8,可得

aij=〈L(Hi(t)),L(Hj(t))〉

bi=〈L(Hi(t)),f(t)〉

4 误差分析

4.1 相关引理

引理9[16](连续模)连续模ω(f,δ)通常被定义为f相对于[a,b]中的δ，

ω(f,δ)=sup{|f(x)-f(y)||x,y∈[a,b],|x-y|≤δ}

(15)

4.2 误差分析

证明：i)由定理1 可得

(16)

ii)

(17)

其中

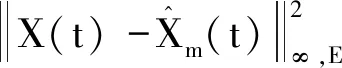
(18)

根据鞅等距性质和Doob不等式，以及(16)～(18)可得

≤3T2(1+T2M2+4TM2)ω(X,h)→0,当h→0.

定理1得以证明。

5 数值算例

图1

表1

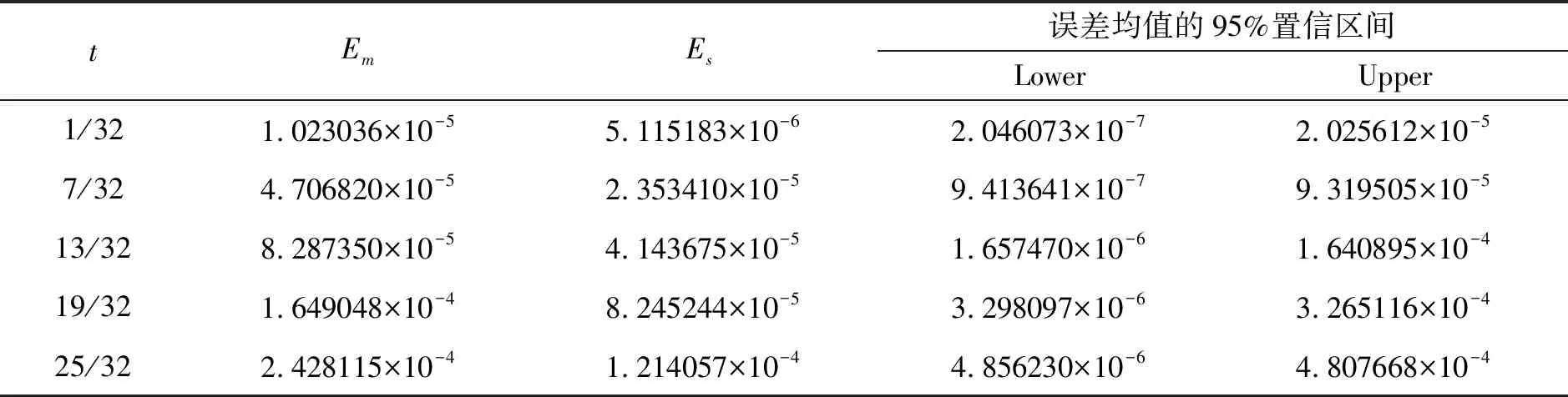
表2

从图1、图2和表1、表2可以看出，近似解与真解非常接近。该方法比文献[16]中的方法得到的结果更加准确，并且验证了该方法对求解随机It-Volterra积分方程是有效的。

图2