三维TTI介质弹性波相、群速度的近似配方表征法
孙上饶 梁 锴 印兴耀 曹丹平 李 坤
(中国石油大学(华东)地球科学与技术学院,山东青岛,266580)
0 引言
横向各向同性(TI)介质广泛存在于地下,如周期性薄互层、裂隙定向排列地层等。实际地下TI介质对称轴的取向往往沿空间任意方向分布,称为任意空间取向TI介质(ATI介质)[1]。当TI介质对称轴与垂直方向存在一定夹角,但方位限定在入射平面内时就称为TTI(Tilted Transversly Isotropical)介质。对于倾斜地层,TTI模型相比于VTI和HTI模型更符合实际地层特征。
各向异性介质的相速度是相角的函数,群速度是相速度的函数,二者均是描述波传播特性的重要参数。通过求解Christoffel方程可以得到TTI介质相速度的精确表达式[2-5]。TTI介质qP波、qSV波相速度和群速度精确表达式各包含四个独立弹性参数。Alkhalifah等[6-7]的研究表明,这四个参数中的三个参数的组合即可较高精度地描述qP波和qSV波的传播特征。然而,由于TTI介质弹性波相速度的表达式过于复杂,难以用于实际地震资料处理,以较为精确的近似表达式替代精确表达式以进行速度分析就显得尤为重要,为此提出了TI介质相速度和群速度的多种近似方法[5,8-19]。Fowler[12]对VTI介质相、群速度十余种不同的近似式进行了系统地比较和讨论,指出对于P波相速度,大多数近似方法有着足够精度以满足实际资料处理的需求;而对于SV波,由于其速度小于P波速度,所以SV波近似中的相对误差往往大于P波,并且由于VTI介质中的相速度具有显式的解析解,与相应的群速度相比,相速度更容易近似。Fomel[14]对Dellinger等[20]的近似方法进行了详细对比分析,提出用三个参数代替精确表达式中的四个参数。Aleixo等[21]和Golikov等[22]比较了几种群速度近似的精度。中国也有多位学者对TI介质体波速度特征开展了深入研究,并应用于地震波正演和偏移等[23-28]。吴国忱等[29-30]推导了三维空间TTI介质弹性波相速度的精确表达式及其弱各向异性近似;李芳等[31]在计算各向异性介质速度的过程中考虑了剪切波的奇点特性,提出了任意各向异性介质弹性波相速度和群速度计算方法;梁锴等[32]推导了倾斜椭球各向异性介质的相速度和群速度表达式,并分析了Thomsen各向异性参数对相、群速度传播特征的影响;谷一鹏等[33]提出了VTI介质弹性波相速度的扩展各向异性线性近似,该方法可以通过控制精确相速度曲线与扩展各向异性线性近似曲线的切点,使该近似在不同程度的各向异性介质中取得较高的精度。由于弱各向异性近似假设并不能很好地适应页岩等中强各向异性介质,因此梁锴等[34]基于近似配方法的思想,推导了二维TTI介质qP波和qSV波相速度一般性近似,数值示例表明该近似相速度可适用于中强各向异性介质。
本文以基于近似配方法的TTI介质弹性波二维相速度近似式[34]为基础,在原有近似中引入方位角,推导了三维相速度的近似式,进而根据Berryman公式[35]导出了基于近似配方法的群速度近似式。利用两组介质模型参数对相、群速度精确值和近似值进行了数值计算,探讨了该近似相、群速度在不同各向异性参数组合下的相对误差,并进行了适用性分析。
1 TTI介质精确和近似弹性波相、群速度
1.1 TTI介质弹性波相速度的精确表征
在进行地震波正演模拟时往往需要将各向异性介质的刚度矩阵从本构坐标系变换到观测坐标系。基于坐标变换方法,定义TTI介质本构坐标系O(x′,y′,z′)和观测坐标系O(x,y,z)如图1所示,其中θ0为TTI介质对称轴Oz′与观测坐标系z轴的夹角,极角θ为传播矢量k与z轴的夹角,方位角φ为传播矢量k在Ω平面上的投影与x轴的夹角。利用Bond变换[36]可以将TI介质本构坐标系下的刚度矩阵转变为观测坐标系下的刚度矩阵。
将平面波解代入TTI介质波动方程,得到TTI介质的Kelvin-Christoffel方程为
(1)
式中:Γij(i,j=1,2,3)为Christoffel矩阵元素;px、py、pz为偏振方向的三个分量。令式(1)系数矩阵行列式为零,可求解得到TTI介质的qP波、qSV波和SH波的相速度精确表达式
(2)
式中
(3)

(4)
其中:vP0和vS0分别为qP波和qSV波沿TTI介质对称轴方向传播的相速度;ε为度量qP波各向异性强度的参数;γ是度量横波分裂强度的参数,当γ=0时,SH波无各向异性;δ为表征TTI介质对称轴方向qP波相速度曲线凹凸性的参数。
将Thomsen参数表征的VTI介质刚度矩阵元素(式(4))代入TTI介质弹性波相速度的精确表达式(式(2))中,可得由Thomsen参数表征的TTI介质弹性波三维相速度表达式
(5)
式中
(6)
TTI介质弹性波的相速度表达式较为复杂,常见的弱各向异性近似、椭圆各向异性近似等可以在一定范围内对精确式进行简化,但在中强各向异性介质中,这些近似相速度误差较大,进而影响速度分析以及偏移处理的精度。
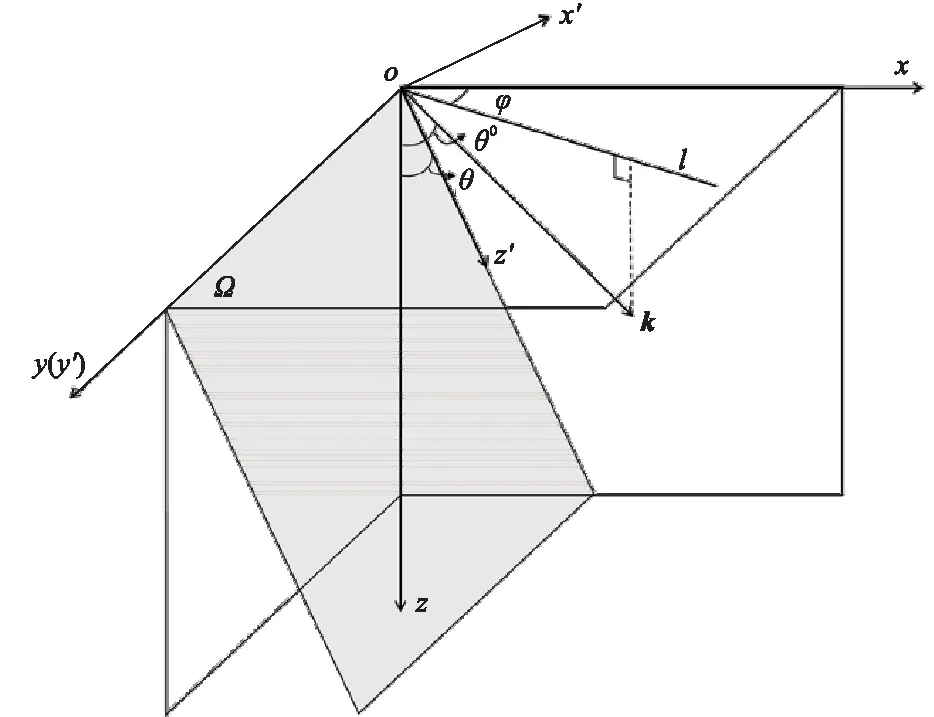
图1 TTI介质本构坐标系与观测坐标系的关系示意图
1.2 TTI介质弹性波相速度的近似表征

从TTI介质弹性波相速度精确表达式(式(5))出发,提取P波和SV波精确相速度存在的共同项
(7)
令
(8)
(9)
则D可以表示为
D=a2+2ab+b2+
[2ε(E2+F2)+(δ-ε)(E2+F2)G2]
(10)
采用如下近似
[2ε(E2+F2)+(δ-ε)(E2+F2)G2]
(11)
则有
(12)
将上式代入相速度精确表达式(式(5))就可得到基于近似配方法的TTI介质qP波和qSV波三维相速度近似式
(13)

(14)
上式与椭圆各向异性情况下精确相速度的形式完全相同[32]。
1.3 TTI介质弹性波群速度的近似表征
各向异性介质地震波群速度决定了地震波能量传播的速度和方向,在地震波旅行时的正演和反演中起着重要的作用。均匀各向异性介质中群速度是相速度的函数,群速度计算一般可以用Berryman公式[35]表示为
(15)
式中k=(kx,ky,kz),为弹性波波矢量,其模k=ω/v,其中v为弹性波相速度、ω为角频率。
根据前人推导TTI介质弹性波群速度的思想[40-41],将相速度近似式(13)代入式(15)中,就可得到TTI介质弹性波群速度的近似表征。其中qP波群速度的近似表征为
(16)
式中
(17)
其中
(18)
qSV波群速度的近似表征为
(19)
式中
(20)
在椭圆各向异性情况下,式(17)可退化为
(21)
式(20)中相速度对极角和方位角的偏导数∂vSVa/∂θ和∂vSVa/∂φ为零。这样,TTI介质椭圆各向异性情况下的近似群速度表达式就可等同于精确群速度表达式。
2 数值示例
本文推导的三维TTI介质qP波和qSV波相、群速度的近似表达式在形式上较精确表达式更为简洁。选取Vernik等[42]给出的两个页岩模型(均为中强各向异性介质(表1))验证本文基于近似配方法的TTI介质弹性波三维相、群速度近似表征的正确性。
2.1 相、群速度数值试算
基于本文近似配方法的三维TTI介质弹性波相、群速度近似表达式,分别计算模型Ⅰ和模型Ⅱ的相速度和群速度。图2为模型Ⅰ和模型Ⅱ的三维近似qP波和qSV波相速度曲面,对应的xOz、yOz、xOy面的近似相速度曲线与精确相速度曲线的对比如图3所示。利用相同的模型可以得到三维近似群速度曲面(图4)及其近似的群速度曲线(图5)。由图2、图4可见,近似和精确相、群速度在三维空间中的速度特征相似。由图3、图5可见本文的近似相、群速度表达式在中强各向异性情况下可以保持较高的精度。
由图3可见,在沿TTI介质对称轴方向(图中黑色短线方向)以及垂直对称轴方向传播时,近似qP波和qSV波相速度与精确值的误差最小,而在与对称轴呈45°方向附近的误差较大。由qP波近似相速度公式(式(13))可看出vS0对P波相速度的影响可以忽略不计,因而影响P波相速度的参数主要为vP0、ε和δ;而影响qSV波的参数则为vP0、vS0、ε和δ,用组合参数σ替代上述四个参数可以减少参数数量,便于描述qSV波的运动学特征;参数σ越大,相速度的近似值与精确值的差异也越大。图5呈现的近似群速度特征与近似相速度特征相似,即在对称轴方向及垂直对称轴方向误差最小,在45°方向附近误差较大。

图2 近似的三维TTI介质相速度曲面(a)模型Ⅰ,qP波; (b)模型Ⅰ,qSV波; (c)模型Ⅱ,qP波; (d)模型Ⅱ,qSV波

图3 近似(蓝色虚线)和精确(红色实线)的三维TTI介质相速度曲线对比(a)模型Ⅰ,xOz面; (b)模型Ⅰ,yOz面; (c)模型Ⅰ,xOy面; (d)模型Ⅱ,xOz面; (e)模型Ⅱ,yOz面; (f)模型Ⅱ,xOy面

图4 近似的三维TTI介质群速度曲面(a)模型Ⅰ,qP波; (b)模型Ⅰ,qSV波; (c)模型Ⅱ,qP波; (d)模型Ⅱ,qSV波

图5 近似(蓝色虚线)和精确(红色实线)的三维TTI介质群速度曲线对比(a)模型Ⅰ,xOz面; (b)模型Ⅰ,yOz面; (c)模型Ⅰ,xOy面; (d)模型Ⅱ,xOz面; (e)模型Ⅱ,yOz面; (f)模型Ⅱ,xOy面
2.2 相对误差分析

2.3 适用性分析
研究表明,沉积地层中ε取值范围从中等各向异性地层的0.1~0.3到压实页岩地层的0.3~0.5,甚至更高[5,43]。为了方便讨论本文的相、群速度近似公式对不同程度各向异性介质的适用性,给定轴向纵、横波速度分别为vP0=4.19km/s、vS0=2.57km/s,θ0=45°,选取[0,0.8]内的ε、δ参数组合,对近似计算的相速度和群速度进行相对误差分析,其最大相对误差等值线如图8所示,可见大部分各向异性参数组合对应的qP波相、群速度的相对误差小于qSV波。在图中对角线处,ε=δ,表示椭圆各向异性,最大相对误差均为零,与理论相符。随着参数|ε-δ|的增大,近似的相、群速度的最大相对误差也越大。对比图8a和图8b可知,在δ远大于ε的较为极端情况下,组合参数σ值更大,导致qSV波相、群速度相对误差远大于qP波。

图6 本文近似计算的TTI介质三维相速度相对误差曲面(a)模型Ⅰ,qP波; (b)模型Ⅰ,qSV波; (c)模型Ⅱ,qP波; (d)模型Ⅱ,qSV波

图7 本文近似计算的TTI介质三维群速度相对误差曲面(a)模型Ⅰ,qP波; (b)模型Ⅰ,qSV波; (c)模型Ⅱ,qP波; (d)模型Ⅱ,qSV波
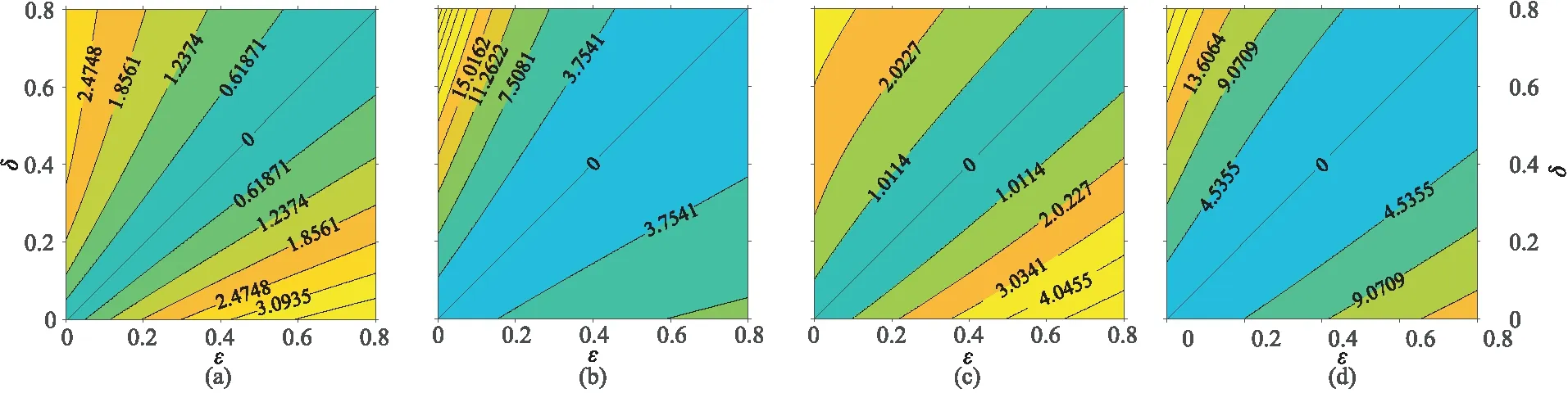
图8 近似的三维TTI介质相、群速度最大相对误差(%)随ε、δ的变化等值线图(a)qP波相速度; (b)qSV波相速度; (c)qP波群速度; (d)qSV波群速度
由图8还可以看出,TTI介质近似qP波相、群速度在弱、中强各向异性情况下与精确解吻合较好;qP波近似相、群速度相对误差在ε>δ时要大于ε<δ时,而qSV波近似相、群速度相对误差则相反;ε与δ越接近,qP波和qSV波近似相、群速度的精度越高。
3 结论与认识

利用本文基于近似配方法推导TTI介质弹性波近似相、群速度的思想,可以进一步研究TTI介质弹性波近似频散关系方程,通过近似频散关系方程可推导出近似解耦的波动方程;可将qP波和qSV波相速度的近似表征代入TTI介质Christoffel方程,求解出偏振矢量的表达式,以探讨TTI介质qP波和qSV波反射、透射特征。此外,在非双曲线速度分析和叠前时间偏移的应用中,群速度近似表征可用于动校正处理和旅行时的计算等。

