基于灰色关联-模糊综合评判的雷达抗干扰性能评估方法
张军涛, 李尚生, 王旭坤
(海军航空大学岸防兵学院, 山东 烟台 264000)
0 引 言
面对日益复杂的电磁对抗环境,正确评估雷达的抗干扰性能对提升武器装备性能具有重要的意义[1-2]。由于干扰样式的多样性以及雷达抗干扰性能评价指标体系的复杂性,客观、全面地评估雷达的抗干扰性能具有一定难度[3-9]。常用的雷达抗干扰性能的评估方法有层次分析法[10-11]、神经网络法[12-14]、可拓学法[15-16]、模糊综合法[17-20]、基于Vague集法[21-22]、灰色关联分析法[23-25]等。层次分析法根据专家经验对雷达抗干扰性能评估指标打分,给出相应的判断矩阵,经过一致性检验后,可以得到评估结果,主观因素对结果有影响。基于神经网络法对雷达抗干扰效能的评估,降低了人为主观性的影响程度,但是训练样本的选取存在一定困难,样本选取的不完备给评估的结果造成偏差。可拓学法以物元模型与可拓集合理论为基础,计算待评方案与评价等级的关联度的大小来确定雷达抗干扰性能的评价等级,局限于特定环境与干扰。模糊综合法通过构造隶属函数建立评判矩阵,计算模糊综合评断结果来明确评估等级,但相同评估等级中无法进行排序。基于Vague法通过对评价指标模糊值的求取,构建模糊值线性评价模型,来确定评价对象的好坏顺序,评价对象的等级无法确定。灰色关联分析法通过计算雷达抗干扰性能的关联度来确定雷达的抗干扰性能的好坏顺序,而抗干扰性能的等级无法确定。各种方法都有特定的优势,但也都有一定的局限性。
模糊综合评价是以模糊数学为基础,应用模糊关系合成的原理,将一些边界不清、不易定量的因素定量化,从多个因素入手对被评价事物隶属等级状况进行综合性评价的一种方法[26-27]。灰色关联评价以灰色理论为基础,计算各方案与最优方案之间的关联度,根据关联度的大小对评价对象进行比较、排序[28]。目前,模糊综合评判应用于雷达抗干扰性能的评估,得到较为客观的雷达抗干扰性能评估结果。但在进行模糊综合评判时,需要确定评价指标的权重,通常是专家主观赋权,或者应用层次分析法赋权,主观影响程度较大。本文通过灰色关联计算评价指标的权重,通过关联度的大小来确定最优权重,进一步降低了评估指标主观赋权对评价结果的影响,有效提高评估的客观性。同时在基于模糊综合评价确定评估对象等级的基础上,基于Vague集模糊值线性序法对评估对象进行排序,进一步确定雷达抗干扰性能评估的优劣顺序。
1 雷达抗干扰性能综合评估指标体系
雷达抗干扰性能的评估是在电磁对抗环境背景下,基于一定的技战术应用准则,采取相应的抗干扰措施,在外场进行试验,结合自身的性能指标,通过大量的数据处理分析来得到。故雷达的抗干扰性能评估指标体系由自身的工作性能和外部的电磁环境特征组成,如图1所示。自身的工作特性包括:雷达的探测信号平均功率,工作频段和采取的抗干扰措施;外部的电磁环境特征包括:雷达所处的电磁环境,干扰对抗的时机[29]。
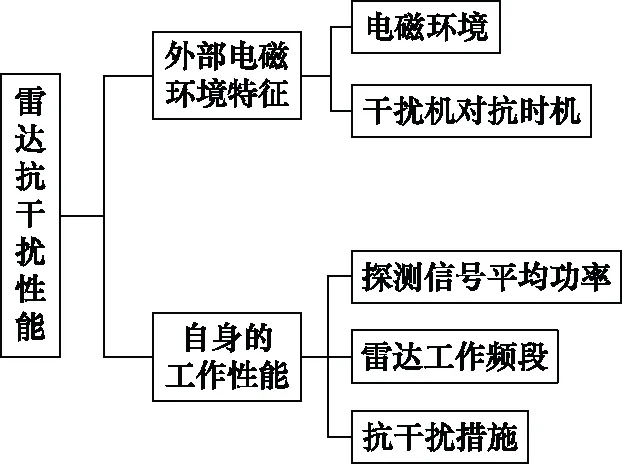
图1 雷达抗干扰性能评价指标Fig.1 Evaluation index of radar anti-jamming performance
1.1 探测信号平均功率
雷达抗干扰性能评估准则常用的有功率准则、信息准则和效率准则。功率准则采用雷达的信干比来描述其抗干扰能力,在干扰功率一定的情况下,增大雷达的发射功率,就能提升信干比,从而改善抗干扰性能。
雷达的探测信号平均功率指标用探测信号平均功率因子U1表示如下:
(1)
式中,S和J分别为信号功率和干扰功率;(S/J)min为雷达可检测的最小信干比。
当(S/J)<0.5(S/J)min时,U1为0;当(S/J)≥2(S/J)min时,U1为1;当0.5(S/J)min≤(S/J)<2(S/J)min时,U1为(2((S/J)/(S/J)min-0.5))/3。U1越大,表明抗干扰能力越好。
1.2 雷达工作频段
当干扰信号的频段和雷达的工作频段重合的部分越大,干扰信号进入雷达接收机的可能性就越大,雷达的抗干扰性能变差。雷达工作频段指标用雷达工作频段重合因子U2来表示:
(2)
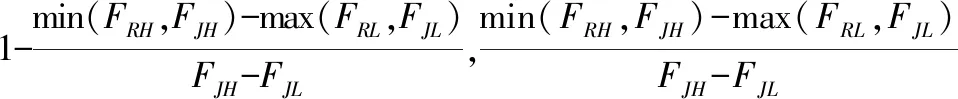
1.3 抗干扰措施
雷达通常的抗干扰措施包括:① 阻止干扰信号进入雷达系统;② 采用信号处理、数据处理等技术来抑制干扰信号。抗干扰措施评价指标用抗干扰措施因子U3来表示:
(3)
式中,假设雷达采取了n种抗干扰措施,第i种抗干扰措施对雷达抗干扰性能的贡献度为ei;ki=1表示雷达具有第i项抗干扰技术措施,否则ki=0。U3越大,雷达抗干扰效能越好。
1.4 雷达电磁环境
雷达所处的电磁环境越复杂,受到的电磁干扰就越多,雷达的抗干扰能力就相对越弱,对目标回波信号的提取就越困难,雷达所处的电磁环境指标用电磁环境因子U4表示:
(4)
式中,ρ为信号流密度(万个脉冲/s)。U4越大,表明抗干扰效果越好。
1.5 干扰机对抗时机
在雷达搜索、截获、跟踪的不同工作阶段,干扰机有效作用时间越长,雷达受到的干扰就越大。干扰机对抗时机指标用干扰机对抗时机因子U5来表示:
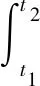
(5)
式中,t1和t2分别表示干扰机有效干扰时间的起点和终点;U5(t)表示有效干扰时间效益函数。U5越大,抗干扰效果越好。
2 基于灰色关联-模糊综合评判雷达抗干扰性能评估模型
通过对雷达抗干扰性能指标的分析,构建了雷达抗干扰评价体系,应用模糊数学的处理方法,对各因素建立相应的模糊数学模型并进行灰色关联-模糊综合评估,流程如图2所示。
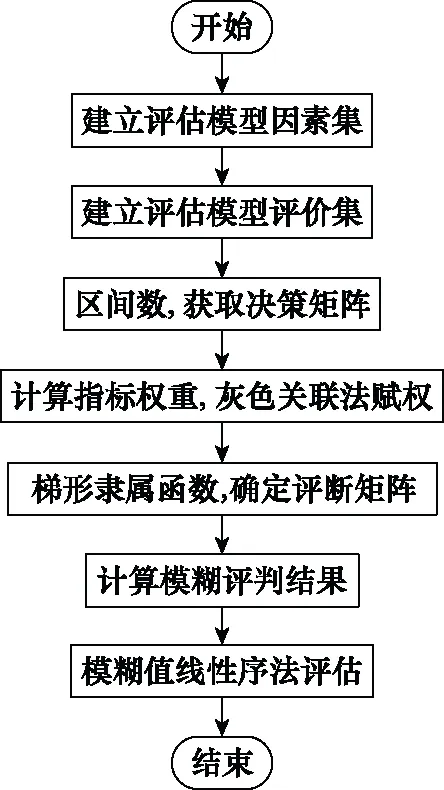
图2 灰色关联-模糊综合评估流程图Fig.2 Flow chart of grey correlation-fuzzy comprehensive evaluation
2.1 建立评估模型因素集
基于建立的雷达抗干扰性能评估指标体系,可得雷达抗干扰性能模糊综合评判的因素集为
U={U1,U2,U3,U4,U5}
式中,U1为探测信号平均功率因子;U2为雷达工作频段频率重合因子;U3为抗干扰措施因子;U4为电磁环境因子;U5为干扰机对抗时机因子。
2.2 建立评估模型评价集
将雷达的抗干扰性能评估指标划分为不同的评价等级,建立评价集如表1所示。

表1 评价集
2.3 建立评估模型因素权重集
雷达抗干扰性能的指标对雷达抗干扰性能的贡献程度不一致,需要确定评价指标的权重,本文参照文献[28],基于灰色关联法确定评价指标权重,相对于文献[29]的主观赋权,得到的雷达抗干扰性能评估结果更为客观。具体通过专家的区间数打分获取决策矩阵,分数大小体现了评价指标的重要程度,通过如下步骤获取专家权重。
步骤 1熵权法求取指标权重
计算离差矩阵D=(dij)n×n
(6)
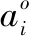
步骤 2计算指标的熵值ei
(7)
式中,k为常数,j=1,2,…,n。当qij都相等时,即qij=1/n,此时熵值最大emax=k·lnn=1,得k=1/lnn。
步骤 3计算指标的偏离程度di
di=1-ei
(8)
归一化得到指标权重wi,从而得到向量Wi=[w1,w2,…,wn],i=1,2,…,c,c为专家数量。
步骤 4用灰色关联度分析的方法确定专家的权重V被比较序列与参考序列的关联系数:
(9)
利用灰色关联分析的方法确定专家的权重,关联度为
(10)
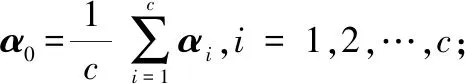
关联度归一化后得到专家的权重V。
步骤 5计算权重G
G=VW*
(11)
式中,W*=[W1,W2,…,Wc]T。
2.4 确定评估模型隶属函数
因素集与评价集之间的模糊关系用评判矩阵来表示,隶属函数用来确定评判矩阵。本文采用模糊分布法中的梯形隶属函数[10,30]来确定雷达抗干扰性能评估因素集和评估模型评价集间的评断矩阵,具体如下:
(12)
式中,ai为雷达各评价指标的评价值;x1和x2分别为各评价等级的区间边界值。
各因素的评判矩阵为
(13)
2.5 模糊综合评价
模糊综合评价结果计算如下:
Bi=GRi,i=1,2,…,c
(14)
2.6 模糊值线性序法评估
参照文献[29],通过评价指标的规范化处理,评价指标的模糊值求取,模糊值线性序构造,模糊优先矩阵构造并排序,对已得到抗干扰评估等级的雷达进行进一步评估,得到待评价雷达抗干扰性能的好坏顺序。
3 应用实例
选取3种不同类型的待评价雷达,根据5种雷达抗干扰性能指标的分析,建立评估模型因素集U={U1,U2,U3,U4,U5}。
参照文献[29]提供的数据,各雷达在每个指标下的评价值见表2。

表2 评价参数表
邀请3位专家采用区间数对评价指标打分,区间数打分的决策矩阵分别为
通过灰色关联分析确定评价指标权重。按照步骤1~步骤3,归一化后求取指标权重。
W1=[0.147 0,0.350 9,0.205 4,0.249 3,0.047 3]
W2=[0.195 0,0.194 4,0.175 9,0.222 6,0.212 1]
W3=[0.185 7,0.155 5,0.421 6,0.064 1,0.173 0]
按照步骤4计算得到雷达抗干扰性能关联系数为
ξ1=[0.559 4,0.556 1,1,0.791 4,0.532 4]
ξ2=[0.722 8,1,0.825 1,1,0.664 1]
ξ3=[1,0.715 5,0.602 6,0.587 7,1]
计算得到雷达抗干扰性能关联度为:R1=0.687 8,R2=0.842 8,R3=0.781 4,归一化后得到专家权重:
V=[0.297 6,0.364 4,0.338 0]
由G=VW*计算得到雷达抗干扰性能评价指标权重:
G=[0.177 6,0.227 8,0.267 7,0.177 0,0.149 8]
通过梯形隶属函数来确定雷达抗干扰性能评估因素集和评估模型评价集间的评断矩阵分别为
按照模糊评判式(14)计算,归一化后可得
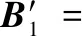
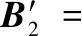
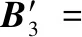
根据隶属度最大原则,雷达X1和雷达X2的抗干扰性能评价为好,雷达X3的抗干扰性能较好,与专家评断相吻合。
对效益型指标U1,U2,U3,U4,U5分别规范化可得各评价指标的模糊值表示:
X1={(U1,[1.00,0.00]),(U2,[1.00,0.00]),
(U3,[1.00,0.00]),(U4,[0.00,1.00]),(U5,[0.00,1.00])}
X2={(U1,[0.79,0.21]),(U2,[0.00,1.00]),
(U3,[0.79,0.21]),(U4,[1.00,0.00]),(U5,[0.93,0.07])}
X3={(U1,[0.00,1.00]),(U2,[0.15,0.85]),
(U3,[0.00,1.00]),(U4,[0.80,0.20]),(U5,[1.00,0.00])}
对模糊值进行处理得到模糊值矩阵:

对评价指标进行线性排序的结果如表3所示。

表3 评价指标线性排序表
代入权重,得到模糊优先矩阵:
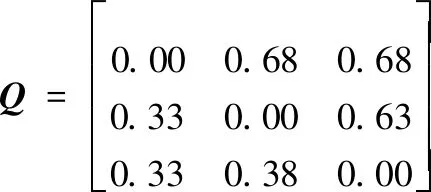
对模糊优先矩阵进行截割,当λ=0.5时,得到截割矩阵:
每行中取1的个数分别是2,1,0,故可得雷达的抗干扰性能的优劣顺序为雷达X1,雷达X2,雷达X3。与文献[29]的雷达抗干扰性能优劣排序结果一致。
文献[29]的评价指标权重通过专家主观赋权,本文通过区间数打分、灰色关联赋权,降低了人为的主观性影响,如表4所示。

表4 评价指标权重
同时通过本文的方法在文献[29]的排序结果的基础上,又能明确雷达抗干扰性能评价等级,即雷达X1和雷达X2的抗干扰性能为好,雷达X3的抗干扰性能较好。文献[19]应用了传统的层次分析模糊综合评价方法,得到的结果是各评价对象的评价等级,当处于相同等级时,评价对象的好坏无法区分。本文可以对处于相同评价等级的对象进行进一步排序,即雷达X1和雷达X2的抗干扰性能为好,雷达X1的抗干扰性能更好。
本文方法可以综合考虑影响雷达抗干扰性能的多方面因素,得到一个定量的抗干扰性能的综合评估结果,证明了该方法的可行性。基于灰色关联法确定的评价指标权重,得到的评价结果较为客观有效。
4 结 论
本文介绍了一种基于灰色关联-模糊综合评判的雷达抗干扰性能评估方法,首先通过分析雷达的抗干扰性能指标,建立雷达抗干扰性能模糊综合评判因素集和雷达抗干扰性能的评价集,通过灰色关联法确定抗干扰性能指标的权重;然后通过梯形隶属函数建立评断矩阵,计算模糊评断结果,根据隶属度最大原则确定评价等级;最后通过评价指标的规范化处理,评价指标的模糊值求取,模糊值线性序构造,模糊优先矩阵构造确定评价对象优劣顺序。与其他分析法相比,基于灰色关联-模糊综合评判的评估方法对雷达抗干扰性能水平能够较全面地评估,灰色关联分析得到的权重比较客观,既能确定评估对象的评价等级,又能进一步排序区分优劣。但是,由于抗干扰的评估指标涉及的要素多,评估准则多样,很难建立完备的评估体系,同时评价等级的区间划分存在一定程度的主观性,影响评估结果,这都是将来需要完善和改进的地方。

