外辐射源雷达目标扇叶微多普勒效应实验研究

占伟杰, 万显荣, 易建新, 谢德强, 程 丰, 饶云华

(武汉大学电子信息学院, 湖北 武汉 430072)

0 引 言

微多普勒效应是由目标主体或部件的微动(如旋转、振动等)引起的多普勒周期性调制现象[1-2]。其与目标的几何结构和运动状态密切相关,被广泛应用于目标参数估计、目标分类识别等领域中[3-8]。因此,有效地获取和利用目标的微动特征,是实现目标信号精细化处理的重要手段。

外辐射源雷达是一种利用第三方发射的电磁信号实现目标探测的双/多基地雷达系统[9-10],相比于常规主动雷达,具有捕获目标微多普勒信息的体制优势,具体表现在:① 主动雷达常利用天线扫描实现对探测区域的覆盖,驻留时间有限；而外辐射源雷达多采用泛探的方式,通过长时间相参积累,一方面有利于弱微动信息的提取,另一方面有利于记录多个周期的微动回波,更好地保证了微动信息的完整性;② 主动雷达需要通过提高发射波形的脉冲重复频率来避免微动频率混叠；而外辐射源雷达常用的照射源(如数字电视信号、调频广播信号等)为连续波形,可以灵活划分快、慢时间(慢时间采样率可等效为脉冲重复频率),提供更多元、合理的参数选择;③ 外辐射源雷达无电磁辐射,易于组网,收发分置的多基地结构为采集微动信息提供了更多自由度,同时也为微动信息的多站融合提供了便利。虽然存在上述优势,但外辐射源雷达发射信号不受控、多径杂波干扰严重等问题也极大地制约了其在微动信息获取中的实际应用,因此当前微动效应的研究仍然以主动雷达为主。

文献[11-12]利用仿真数据对外辐射源雷达中目标微动特征提取的相关问题进行了研究。文献[13-15]展示了基于数字电视信号的外辐射源雷达对风扇和无人机微动回波的初步实验探测结果。文献[16-17]分别利用仿真和实测数据研究了风电机组微动回波在外辐射源雷达中的特征表现。可以看出,外辐射源雷达应用于微动研究领域的可行性已得到理论和实验验证,但相关研究主要针对单类目标进行,缺少对不同类型的目标微动特征较为全面的展示与对比。因此,本文在现有研究基础上,系统总结了武汉大学UHF频段外辐射源雷达目标微动实验的最新进展,展示了包括直升机、通航飞机、无人机、风电机组等目标扇叶转动的微动回波探测结果,分析了各类型目标微动回波在时域、频域、时频分布图、距离-多普勒(range-Doppler, RD)谱上的特征表现,并揭示了微动特征与扇叶相关参数之间的联系,实现了扇叶参数的反演。

1 外辐射源雷达目标扇叶微动信号模型

1.1 外辐射源雷达扇叶微动回波表达式

如图1所示,以接收站R为坐标原点,接收站R与发射站T的连线为X轴正方向建立雷达坐标系XYZ。以目标质心O为坐标原点建立参考坐标系UVW,UVW各个坐标轴均平行于XYZ对应的坐标轴,且随质心运动。

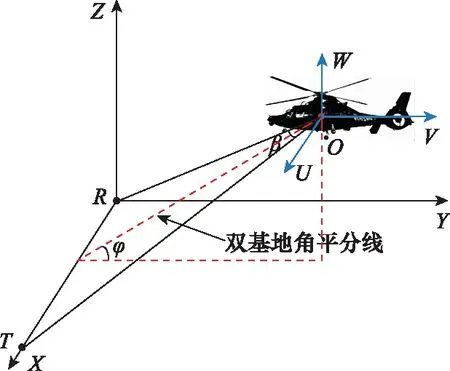
图1 双基地雷达微多普勒探测场景示意图Fig.1 Diagram of micro-Doppler detection scene using bistatic radar

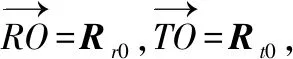
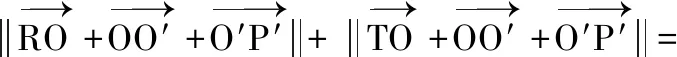
(1)

(2)

则

(3)

所以

(4)

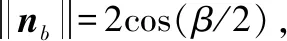
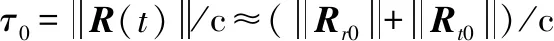
vTnbt+(Rrotaterp)Tnb]

(5)

式中,λ=c/f0表示信号波长,附加相位由3个部分组成:

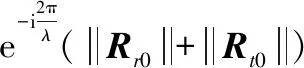
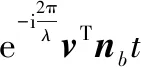
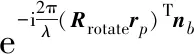
综上,散射点P的回波可以进一步整理为

(6)

设扇叶长度为L,扇叶个数为K,则所有扇叶总回波为

(7)

式中,

sinc(x)=sinx/x

(8)

1.2 扇叶微动回波时域特性分析

由式(7)可以看到,扇叶回波幅值受sinc(·)的影响,表现出周期性调制特征。当扇叶与雷达视线垂直时,扇叶上各点回波同相叠加,出现调制副峰。相邻调制副峰之间的时间间隔ΔT与扇叶数目K和旋转速率Ωm之间的关系如下:

(9)

由图2可知,当扇叶数目为偶数时,每转动2π/K,就会出现一次与雷达视线垂直的情况,且此时同时存在靠近和远离雷达的一对对称扇叶,因此在时频图上表现出正负频率对称的强能量条带(称为flash),一个完整转动周期中包含K个flash;对于奇数扇叶的情况,每转动π/K就会有一个扇叶(靠近或远离雷达)与雷达实现垂直,因此在时频图上表现出正负频率交错出现的flash,一个完整转动周期中包含2K个flash。

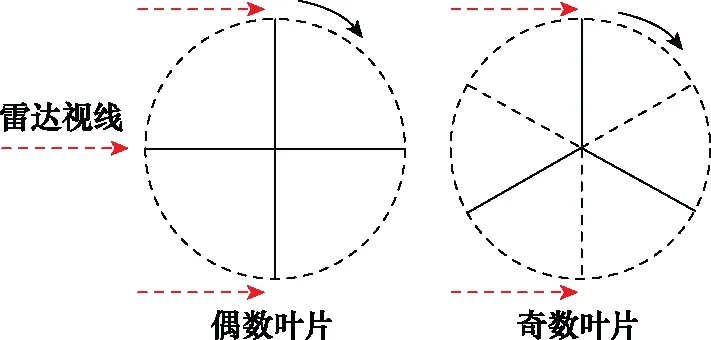
图2 扇叶回波时域周期性与扇叶数目奇偶性的关系Fig.2 Relationship between the time-domain periodicity of blade echo and the parity of blade number

1.3 扇叶微动回波频域特性分析

利用Bessel函数母函数的性质,可以将式(6)改写为

(10)

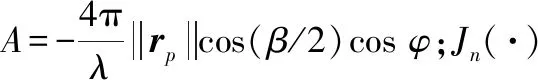
(11)

式中,S(f)为基带信号s(t)的傅里叶变换结果,则其频谱为

完整扇叶回波的频谱可以表示为扇叶上所有散射点回波的频谱之和,即式(7)的频谱[19]可以近似表示为

(12)

可以看出,扇叶回波频谱包含一系列以目标平动多普勒频率为中心左右对称且频率间隔为Δf=KΩm/2π的谱峰。σn表示每个谱峰的幅值,由扇叶上所有散射点的回波幅度和第一类Bessel函数的值等参数决定。上述模型仅考虑了扇叶回波,并未考虑目标主体回波,通常情况下目标主体回波强度大于扇叶回波,且其多普勒频率仅由目标平动造成,因此实际情况下,中心谱峰的强度会大于左右两边谱峰强度。M=8π/K·L/λ·cos(β/2)cosφ表示调制谱线个数,则调制带宽可以表示为B=M·Δf=4LΩm/λ·cos(β/2)cosφ,该带宽包含了回波的大部分能量。

1.4 扇叶微动回波的距离像

外辐射源雷达通常设置参考通道和监测通道,设sref(t)为参考信号,ssurv(t)为监测信号,则RD谱可表示为

(13)

式中,Tint表示相干积累时间,将其表示成快时间和慢时间组成,则式(13)可以整理成

(14)

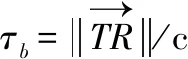
(15)

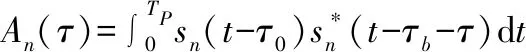
G(n)=σLe-i2πf0 (τ0 -τb )eiΩT nTP·

其中,e-i2πf0(τ0-τb)表示由双基距离差造成的相位偏移。可以看出,目标距离像主要由相位函数Φk(nTP)和发射信号本身的自相关函数决定,满足第1.2节分析的时域周期性。目标距离像的自相关处理结果与其自身具有同样的周期性,且相关峰值更加尖锐,在本文中用于辅助微动周期估计。目标所在距离单元上的RD谱数据为对应位置距离像的傅里叶变换。因此,微动回波在RD谱中具备第1.3节频域周期性质,表现为沿多普勒维周期性分布的调制谱峰。

2 实验结果

本文实验数据均来自于武汉大学研制的多照射源被动雷达(multi-illuminator passive radar, MIPAR)系统[20-21]。利用参考天线接收直达波信号,监测天线阵列接收目标微动回波信号。对参考信号进行提纯,同时对监测信号进行直达波和多径杂波抑制,然后对经过上述预处理后的参考信号和监测信号进行匹配滤波以获取微动分量的距离像[22-24]。通过对距离像进行目标主体分量去除、自相关、时频分析等处理可提取微动特征用于扇叶转速、长度等参数的反演。文中扇叶各参数的估计精度计算如下：

(16)

式中,real和esti分别表示参数的真实值和估计值。

2.1 直升机旋翼微多普勒探测结果

本实验照射源信号频率为658 MHz, 收发站基线长度约为7.5 km。雷达探测对象为2017年武汉国际马拉松比赛期间巡逻直升机[25]。该直升机型号为EC_120B,主旋翼包含3个扇叶,扇叶长度为5 m,额定转速为406 rmp。实验过程中直升机进行先靠近后远离接收站的运动,采集的数据时长约50 s。以下采用0.8 s相干积累时间进行处理。

图3为连续50 s RD谱累积结果,在近处可以看到明显的旋翼转动引入的微多普勒现象。

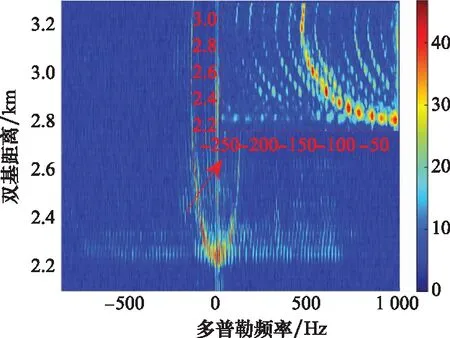
图3 直升机微多普勒效应连续探测结果Fig.3 Continuous detection result of micro-Doppler effect of helicopter

图4为第14个处理周期(对应10.4～11.2 s内的数据)的结果,在该处理周期内目标对应的双基地角β≈40.02°,双基地角平分线与旋转平面夹角φ≈13.82°。图4(a)为RD谱中目标所在距离单元的截面图,图中最强谱峰对应目标主体分量,直升机旋翼引入的微动效应表现为相对目标主峰左右对称的周期性调制副峰。对目标距离谱进行时频变换,得到图4(b)所示时频分布图,可以看到除极强的机身分量外,正负多普勒频率上的flash等间隔交错分布,符合奇数扇叶微动效应的时频分布规律。图4(c)为利用主成分分析(principal component analysis, PCA)算法去除机身分量后的时频分布结果[26],可以看出排除机身分量的影响后,旋翼微动特征表现得更加明显。图4(d)和图4(e)分别为机身分量去除前,由于距离像中机身分量强度远大于旋翼微动分量,因此旋翼微动效应被掩盖;去除机身分量后,旋翼微动效应得以凸显。通过对微动分量的距离像进行自相关处理可以得到更尖锐的周期性调制谱峰,用于后续转速的估计。综合图4结果,可以得到该处理周期内微动效应的相邻谱峰的时间间隔约为24.60 ms, 调制带宽约为1 800 Hz。综合上述微动特征参数,利用第1.2和第1.3节的结论,可估计得到旋翼转速约为406.50 rmp(估计精度约为99.88%),旋翼长度约为5.28 m(估计精度约为94.40%)。

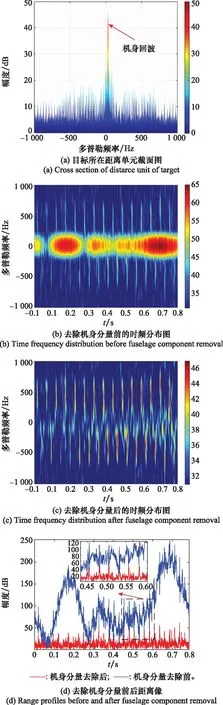
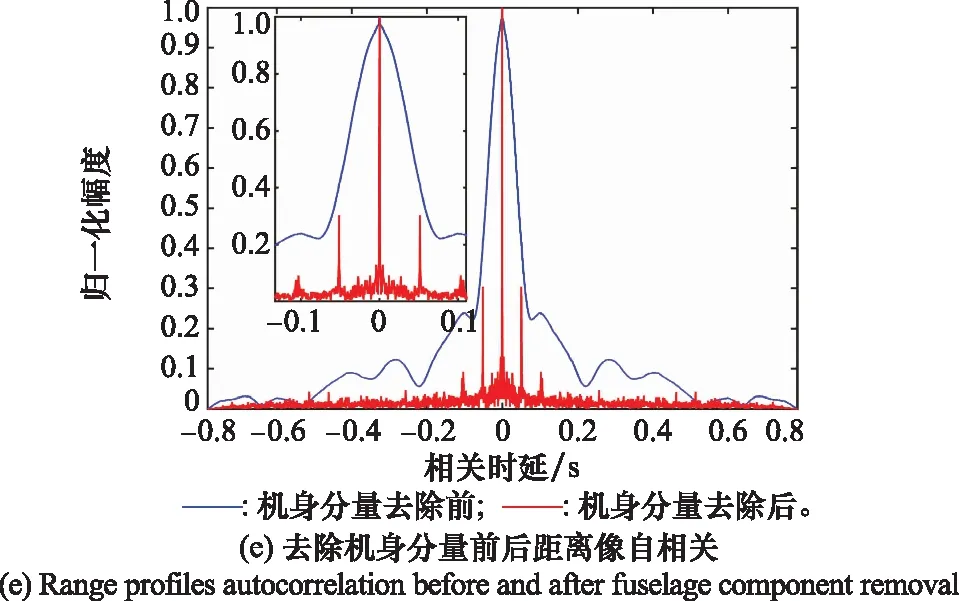
图4 直升机微动效应单个处理周期的结果Fig.4 Results of micro-Doppler effect of helicopter in single processing cycle

2.2 通航飞机旋翼微多普勒探测结果

本实验所用照射源频率为658 MHz, 接收站设置在发射站西南方向约208°,距离约12 km处。在数据采集期间,雷达探测范围内同时存在多架通航飞机,图5为连续387 s的RD谱累积结果,选取西瑞SR20飞机进行后续分析。西瑞SR20为单发飞机,头部有一个3叶片旋翼,其额定转速为2 700 rpm,旋翼直径为1.94 m。以下采用1 s积累时间进行处理。

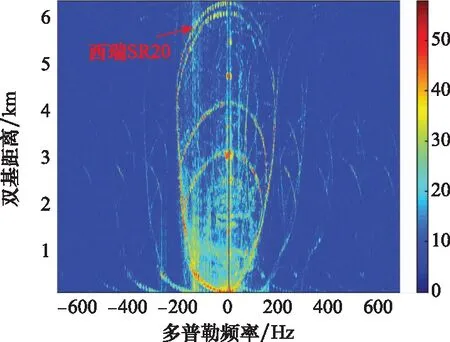
图5 通航飞机微多普勒连续探测结果Fig.5 Continuous detection result of micro-Doppler effect of general aviation airplanes

图6(a)为第300个处理周期中(对应第299～300 s的数据)目标所在距离单元的截面图,该处理周期内目标对应的双基地角β≈29.90°,双基地角平分线与旋转平面之间的夹角φ≈40.06°。图6(a)中强机身分量左右两侧存在周期性分布的微多普勒调制副峰,相邻副峰之间的频率间隔为132.30 Hz。对目标距离像进行时频分析得到图6(b)所示结果,此时微动分量湮没在强机身分量中,无法分辨各个扇叶的flash。图6(c)和图6(d)分别为去除机身回波前后的距离像及其自相关结果,可以得到时域调制谱峰时间间隔约为7.78 ms。图6(e)为去除机身分量之后的时频分布结果,此时相邻flash能被分离开来,呈现正负频率等间隔交错分布,符合奇数扇叶微动效应的时频分布规律。图6中相邻flash之间的时间间隔约为3.90 ms,调制带宽约为1 600 Hz。综合上述微动特征参数,利用第1.2和第1.3节的结论,可估计得到该处理周期内旋翼转速约为2 646 rpm(估计精度约为98.00%),旋翼半径约为0.89 m(估计精度约为91.75%)。

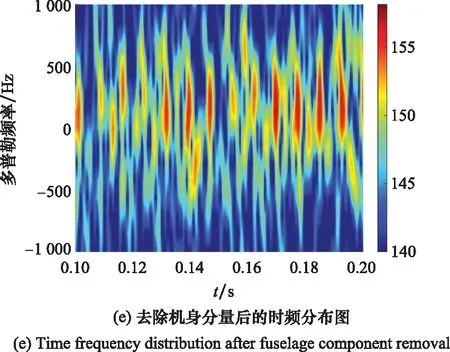
图6 通航飞机微动效应单个处理周期的结果Fig.6 Results of micro motion effect of general aviation in single processing cycle

2.3 无人机旋翼微多普勒探测结果

本实验所用照射源信号频率为658 MHz,收发基线长度约为7.5 km。雷达探测目标为大疆M100多旋翼无人机。该无人机具有4个旋翼,每个旋翼包含2个扇叶,每个扇叶长度为17.25 cm,旋翼最大转速为7 770 rpm,实际悬停或飞行状态下,无人机旋翼转速为最大值的25%～100%[27]。实验过程中将无人机悬停于监测阵列前方309 m,距阵列高度100 m处进行数据采集,双基地角β≈56.95°,双基地角平分线与旋转平面之间的夹角φ≈1.40°[14]。实验数据采集时长约300 s, 以下采用1 s积累时间进行处理。由于无人机处于悬停状态,其机身分量位于零频处,因此机身分量在直达波抑制过程中即可得到有效去除。

图7为连续300 s的无人机微多普勒探测结果,可以看到两条明显的微多普勒调制带,证明了该系统对悬停无人机微多普勒的连续探测能力。

图7 无人机微多普勒连续探测结果Fig.7 Continuous micro-Doppler detection result of unmanned aerial vehicle

取其中第20个处理周期(对应第19～20 s的数据)的探测结果进行详细分析。图8(a)和图8(b)分别为该处理周期中RD谱的俯视和正视图,可以看出此时在-189 Hz和189 Hz附近存在微多普勒调制副峰,调制总带宽约为380 Hz。图8(c)中微动回波距离谱自相关结果表现为明显的周期性相关副峰,且相邻相关峰之间的时间间隔约为5.56 ms。图8(d)为微动回波距离谱的时频分布结果,可以看到正负频率对称分布的flash,符合偶数扇叶微动效应的时频分布规律,相邻flash之间的时间间隔大致也为5.56 ms。综合上述微动特征参数,利用第1.2和第1.3节的结论,可估算得到该处理周期内无人机旋翼转速约为5 398 rpm,占旋翼最大转速的69.47%,在合理区间范围内, 无人机旋翼长度估计值约为17.43 cm(估计精度约为98.96%)。

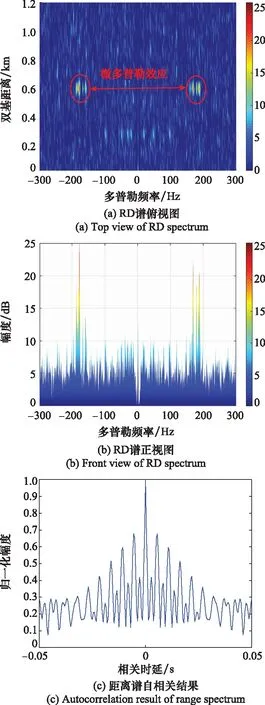
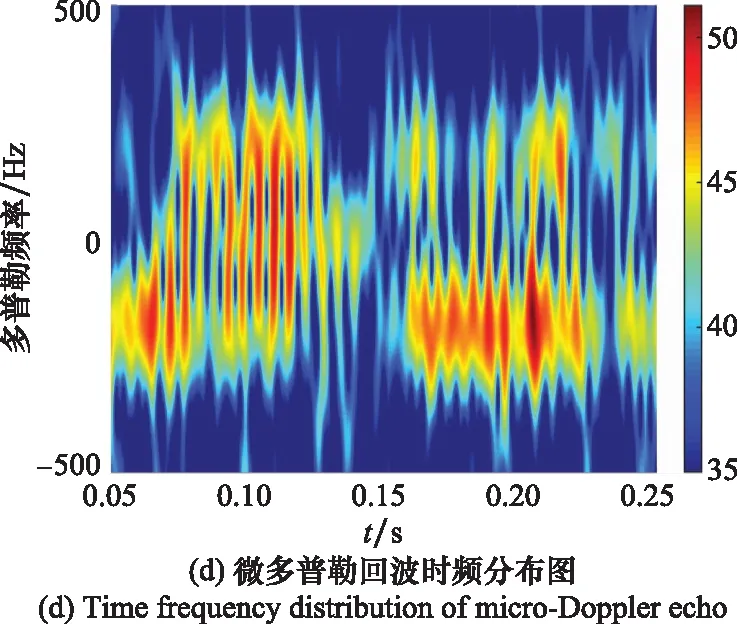
图8 无人机微动效应单个处理周期的结果Fig.8 Results of micro motion effect of unmanned aerial vehicle in single processing cycle

2.4 风电机组扇叶微多普勒探测结果

本实验所用照射源频率为722 MHz,接收站设置在发射站东南方向约106°,距离约20 km处。在约6.7 km的雷达探测范围内分布有12个2 MW的风电机组。机组叶轮直径为118 m, 扇叶长度为56.8 m, 扇叶额定转速为13.32 rpm。因扇叶转速较慢,扇叶微动效应谱峰的频率间隔较小,故需采用较长相干积累时间以提高系统的频率分辨率,本文将相干积累时间设置为12 s。

图9为一个处理周期内的RD谱,从谱中可以看出,各个风电机组所在距离单元上均存在明显的多普勒维调制谱峰。调制谱峰的带宽与各个风电机组扇叶的转速、扇面朝向及对应的探测场景等因素有关。以其中某个风电机组为例进行分析,此时双基地角β≈19.32°,双基地角平分线与旋转平面之间的夹角φ≈62.50°。图10(a)为该风电机组的距离像,其幅度呈周期性调制的形态,对该距离像进行自相关处理,得到图10(b)所示的自相关谱,图中可见明显的周期性分布的尖锐谱峰,相邻谱峰间隔约为1.51 s。图10(c)为该风电机组RD谱的多普勒维截面,从中可得相邻调制谱峰之间的频率间隔约为0.67 Hz,调制带宽约为330 Hz。图10(d)为该风电机组微动回波的时频分布图,图中有16根正负频率交错分布的flash,符合奇数扇叶微动效应的时频分布规律。值得注意的是,每条flash并非呈现垂直于零频线的笔直状态,而是存在一定程度的倾斜和弯曲,这可能是因为扇叶的不规则形状及探测场景不满足远场探测条件等因素,导致实际扇叶微动模型与第2.1节理想模型之间存在一定差异[28]。综合上述微动特征参数,利用第1.2和第1.3节的结论,可估算得到该处理周期内扇叶转动速度约为13.24 rpm(估计精度约为99.40%),扇叶长度约为54.3 m(估计精度约为95.60%)。

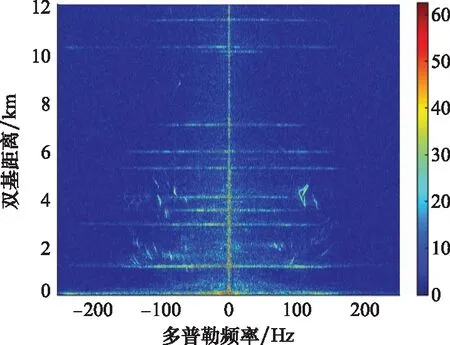
图9 风电机组微多普勒效应探测结果Fig.9 Detection result of micro-Doppler effect of wind turbines

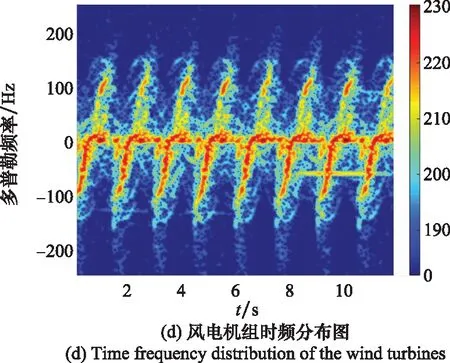
图10 风电机组微多普勒效应探测结果Fig.10 Detection results of the micro-Doppler effect of the wind turbines

3 实验结果分析

本文展示了UHF频段外辐射源雷达对直升机、通航飞机、无人机和风电机组扇叶的微动回波探测结果,具体如下:

(1) 各种类型目标扇叶的微动效应总体上均表现为时域、频域、距离像和RD谱上的周期性调制谱峰,相邻谱峰之间的时间或频率间隔只取决于扇叶个数和转速,调制带宽则取决于信号频率、扇叶转速、扇叶长度及探测场景相关参数。因此,通过实验结果呈现出的微动特征,可以反演目标扇叶的相关重要参数,为后续目标精细化建模及目标分类识别提供支撑。

(2) 运动目标的强主体回波会影响微动特征的提取和利用,因此需要采用额外的信号处理方法减轻目标主体回波的影响(静止目标的主体回波可通过杂波抑制模块去除),常用方法包括PCA、经验模态分解(empirical mode decomposition, EMD)[29]、稀疏分解[30]等。

(3) 相干积累时间应不小于一个完整微动周期,因此对于低速旋转目标需要采用长相干积累时间。慢时间采样率(脉冲重复频率)至少应大于微动最大多普勒拓展频率的两倍,以保证微动回波频谱不发生混叠,同时为了使时频图中相邻flash能够更好地分开,往往需要进一步提升慢时间维采样率。

4 结 论

本文总结整理了MIPAR系统对直升机、通航飞机、无人机、风电机组等目标扇叶的微动回波探测结果。实验结果直观清晰地展示出了上述扇叶微动回波在时域、频域、时频分布图、RD谱上特征表现的差异,揭示了微动特征与扇叶相关参数之间的联系,并成功利用微动特征反演得到了扇叶尺寸、转速等重要参数。后续工作将包括外辐射源雷达微动特征数据库的建立,以及利用微动特征实现目标的精细化建模和目标分类识别。