基于视频图像车速计算的随机误差分析

王 迪 魏 亮 龚 标 吴卓鸿

（1.云南省交通科学研究院有限公司，昆明 650011；2.云南云通司法鉴定中心，昆明 650255；3.公安部交通管理科学研究所，无锡 214151）

基于视频图像车速计算的精度是社会各界一直以来关注的焦点，对基于视频图像车速计算中“时间插值法”数学模型进行的误差分析，就是为了找出误差产生的原因、影响误差的关键因素、降低误差影响的方法等从而提高计算精度，以便更加真实客观地反映车辆行驶的运动状态。

误差是实验科学术语，指测量结果偏离真值的程度。对任何一个物理量进行的测量（检测）都不可能得出一个绝对准确的数值，即使使用测量技术所能达到的最完善的方法或设备，测出的数值也和真实值存在差异，这种测量值和真实值的差异称为误差。基于视频图像车速计算的误差由随机误差和系统误差构成[1]，针对基于视频图像车速计算的随机误差进行分析研究。

1 随机误差产生的原因

以“时间插值法”数学模型为例，分析基于视频图像车速计算中随机误差产生的原因。设目标车辆以100km/h的速度行驶，利用“时间插值法”数学模型进行车速计算的过程，如图1所示。

图1 100 km/h车速分析示意图

首先在视频画面中建立直角坐标系，设车辆沿X轴（水平）方向运动，以轴距为标尺，以某一帧画面为基准，前轮轮心A(标尺终点)的X坐标为a；经过2帧后，后轮轮心运动到B点处，此时B点接近A点，其X坐标为b；再经过1帧后，后轮轮心运动到C点处，此时C点超过A点,其X坐标为c。利用”时间插值法”数学模，计算车辆行驶过一个标尺长度的精确时间。

设视频帧速率为25 fps，则车辆行驶过一个标尺的时间：

T=2×0.04+△t

其中：

△t=0.04×(b−a)/(b−c)

则车辆行驶过一个标尺长度（L）的平均速度：

v=L/(2×0.04+△t)

“时间插值法”就是利用A、B、C三个点的X坐标值a、b、c，计算出车辆驶过一个标尺的时间T的数值，从而计算出车速[2]。因“时间插值法”数学模型中仅有a、b、c的值为测量量或不确定量，故在视频画面中找到A、B、C位置（简称找点，下同）的精度就决定了“时间插值法”的计算精度。

2 影响随机误差的因素

通过大量的工作实践及研究论证，基于视频图像车速计算的精度主要取决于两方面的条件：一是客观条件，主要由视频本身的质量所决定，包括视频图像的清晰度、分辨率、拍摄视频图像的摄像机距离距肇事地点的距离、肇事目标车辆的行驶速度等，这些因素在视频图像拍摄过程中就已决定，在进行车速分析过程中人工无法对其进行干预；二是主观条件，主要由进行车速分析的实际操作人员的技术水平所决定，包括计算模型的选取、计算标尺的选取、操作熟练度等，这些因素在车速计算过程中起作用并直接影响计算精度（仅对计算标尺的选取进行研究）。

在进行车速计算的过程中，主、客观因素同时存在，因客观因素无法改变，故只能在基于现有客观因素的条件下，综合分析，合理选择计算模型、计算标尺等，达到减小随机误差影响的目的[3]。

3 随机误差影响因素的研究

3.1 计算标尺的选取对随机误差的影响

对上例进行广义化，根据“时间插值法”数学模型，T=n×(1/f)+△t，模型中n、f两个参数不依赖于选点精度，仅△t依赖于选点精度。当选取的标尺较长时，目标车辆行驶过一个标尺的时间较长，n值较大，此时△t对T的影响程度较小，随机误差也较小。反之，若选取的标尺较短时，则△t对T的影响较大。设误差为一固定值e，“时间插值法”数学模型中的可靠值为k=n×(1/f)，k是以1为首项，公差为1的等差数列，则e在k中的影响比例如图2所示。

加强相关工作人员的责任心。档案工作目前还存在着，资料归档、整理不及时，工程施工、检查记录与工程施工不同步、资料与实际情况不相符及记录不规范的现象。我们采取了一是项目部设有专人负责工程资料的收集；二是编制了统一的表格，尽量使记录表格化，并细化相关填写标准；三是公司本部及项目部技术人员，分别经常性地组织检查，按检查结果进行奖惩等措施，努力提高管理工作水平。

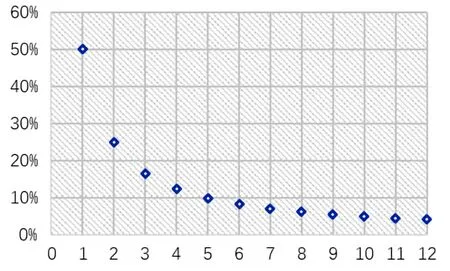
图2 误差占比示意图

因此，运用“时间插值法”数学模型进行车速计算时应尽根据实际情况尽可能的选取较长的标尺以增加可靠值k的比重，降低△t的比重从而减小随机误差的影响。

3.2 目标车辆行驶速度对随机误差的影响

在计算标尺一定的情况下，当目标车辆行驶速度越快时，目标车辆行驶过一个计算标尺的时间越短，可靠值k的比重越低，△t的比重越高，找点的误差对计算误差的影响越大；反之，若行驶车速越低，车辆行驶过一个标尺的时间就越长，可靠值k的比重越高，△t的比重越低，找点误差对计算误差的影响就越小。

例如标尺（轴距）为2.61 m的目标车辆以100 km/h的速度行驶，2帧行驶2.22 m，不足一个标尺长度，3帧行驶3.33 m，超过一个标尺长度。用“时间插值法”数学模型计算车速，得：

v=L/(2×(1/f)+△t)

因△t在分母中所占比重相对较大，故找点误差对计算结果的影响就相对大。

若目标车辆以50 km/h的速度行驶，4帧行驶2.22 m，不足一个标尺长度，5帧行驶2.78 m，超过一个标尺长度。用“时间插值法”数学模型计算车速，得：

v=L/(4×(1/f)+△t)

因△t在分母中所占比重相对较小，故找点误差对计算结果的影响就相对小。

3.3 目标车辆至监控摄像头的距离对随机误差的影响

为了研究目标车辆至监控摄像头的距离对随机误差的影响，研究人员进行了验证试验。试验中目标车辆由远及近驶来，非接触式速度仪记录目标车辆行驶速度，摄像机拍摄视频，见图3。

图3 目标车辆至镜头距离的影响验证试验

研究人员进行了10人次的跟踪找点（跟踪时均是在同一个坐标系下进行），利用“时间插值法”数学模型，以轴距为标尺计算出10组共350个数据（即时间速度相对应的一对数据），绘制时间−速度曲线图，在每一时刻的10个数据中找出最大值（MAX）和最小值（MIN），得到两组数据，将这两组最大最小值数据与非接触式速度仪记录的一组数据（MEA）一并绘入图中，对这三组数据分别进行线型回归，得到三组数据的拟合线，以最大值数据组的拟合线作为上偏差，以最小值数据组的拟合线作为下偏差，则上下偏差之间形成误差带，非接触式速度仪记录的数值位于误差带内，如见图4所示。

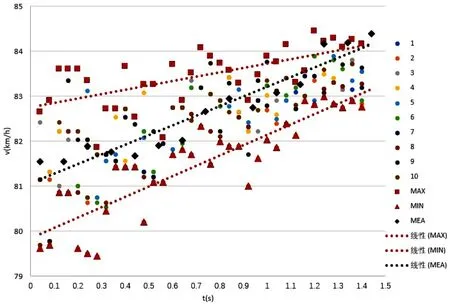
图4 目标车辆距摄像头距离对误差带的影响

在图4中可以看到：总共350个数据中只有32个数据落在了误差带以外，而有近90.86%的数据都落在了误差带内；远端速度波动范围为3 km/h，近端速度波动范围为1 km/h，误差带宽度由远到近逐渐变窄。

研究人员对远端及近端的找点误差（10人次找点X轴坐标值）进行了统计，统计分析显示不管远端还是近端，特征点X坐标值均在1～2个像素范围内波动。所以通过10人次找点试验可以看出，目标车辆距摄像头的距离对找点精度影响不大，如图5所示。

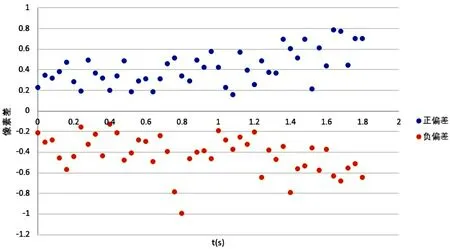
图5 目标车辆距摄像头距离对找点精度的影响

分析认为：远端每个像素代表的实际距离较长，画面中代表一个标尺内的像素数较少，因找点精度问题造成的误差较大，所以计算出的车速误差较大；而近端每个像素代表的实际距离较短，画面中一个标尺内的像素数较多，因找点精度问题造成的误差较小，所以计算出的车速误差小。

3.4 图像清晰度对随机误差的影响

为了研究图像清晰度对随机误差的影响，研究人员分别对模糊图像和清晰图像进行了找点分析。图6展示的是模糊图像找点时的景象，其中下图为图像画面放大6倍之后的情况。

图6 模糊图像找点时的景象

可以看出在模糊图像中找点是相当困难的，研究人员用前述方法，进行了12人次的找点试验，绘制出模糊图像的误差带[4]。通过图7可以看出，当图像模糊时，误差带宽度比较大，均值为13.43 km/h。

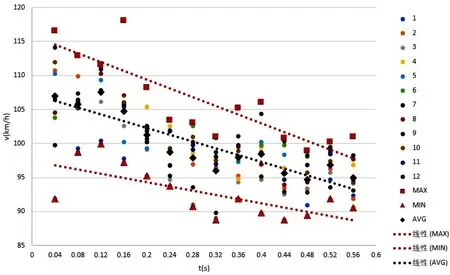
图7 模糊图像的误差带

图8展示的是清晰图像找点时的景象，可以看出与模糊图像找点相比较，清晰图像找点时容易得多。通过图9可以看出，当图像清晰时，误差带宽度比较小，均值仅为1.05 km/h。

图8 清晰图像找点时的景象

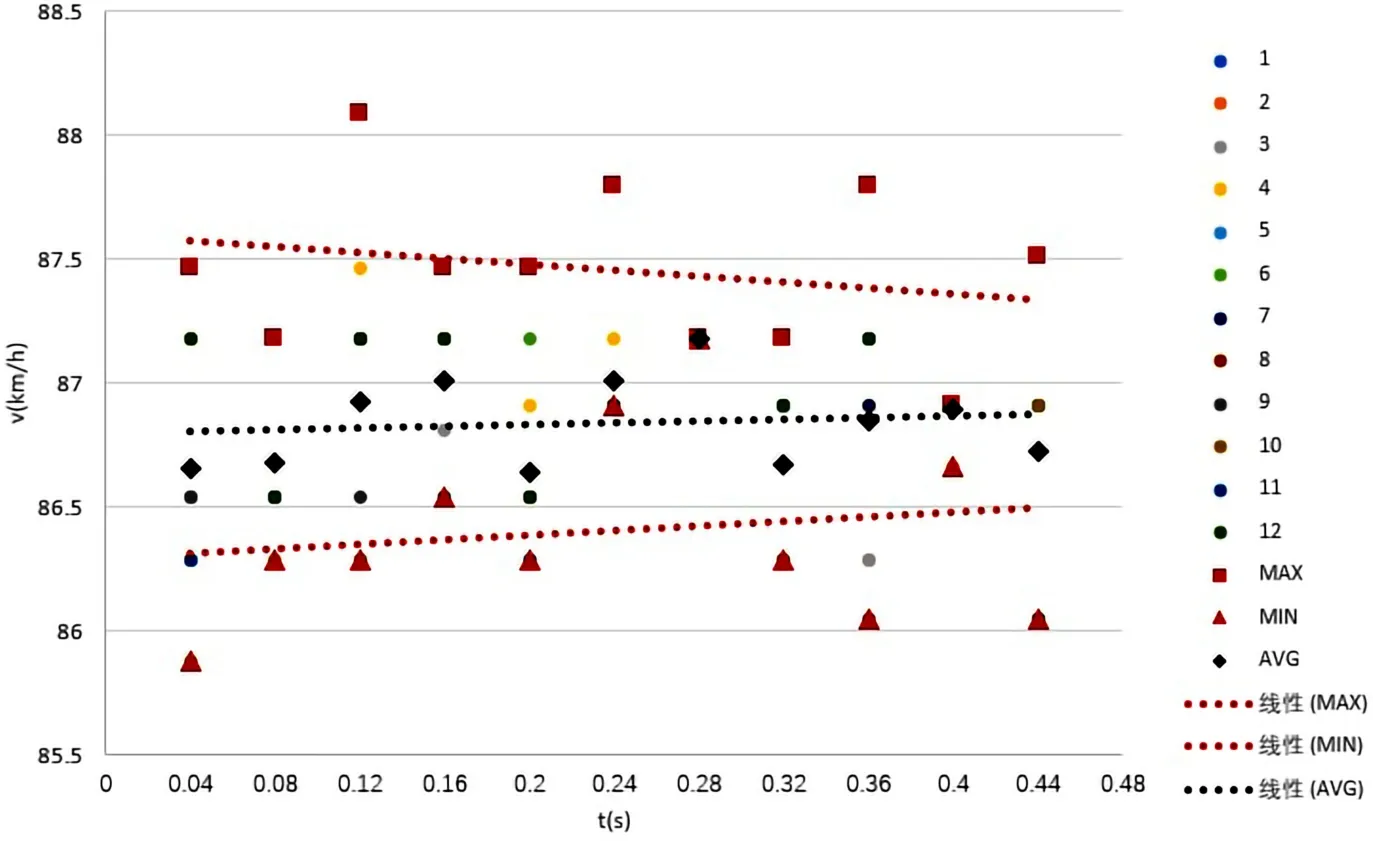
图9 清晰图像的误差带

经过以上分析可以得到结论：视频图像清晰度是造成随机误差的关键因素，根据随机误差的特点，对于图像模糊的视频资料，只能通过加大找点次数采取多次跟踪取均值的办法来尽可能的逼近真值。

3.5 图像分辨率对随机误差的影响

一般情况下，跟踪点的X、Y坐标是以像素为单位的。对于704×576的视频，X坐标范围是0—704，Y坐标范围是0—576；对于1920×1080的视频，X坐标范围是0—1920，Y坐标范围是0—1080，以此类推。

图10展示了不同分辨率下搜索特征点真实位置的情况（在这里以方形像素为例，实际中像素有多种形状），其中设O点为特征点真实位置。由于像素不是一个无限小的点而是一个微小单元，所以要搜索到特征点的真实位置几乎是不可能的。如果拍摄同一个物体，在低分辨率情况下，每个像素所占单元比高分辨率情况下每个像素所占的单元要大。单元ABCD代表低分辨率的一个像素，单元A′B′C′D′代表高分辨率的一个像素，低分辨率下跟踪点A比跟踪点B更接近于O，高分辨率下跟踪点B′比跟踪点A′（A）更接近于O。以上分析说明分辨率越高，就越容易找到逼近特征点真实位置的跟踪点，由于跟踪点与特征点真实位置越近，计算分析结果越准确，所以高分辨率图像的计算结果比低分辨率图像的计算结果更精确。

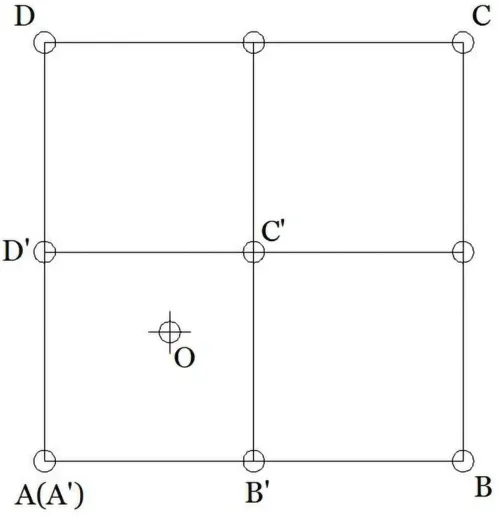
图10 不同分辨率下搜索特征点的真实位置

为研究不同图像分辨率下的随机误差，对同一段视频图像进行了分辨率处理，得到视频图像高、低分辨率的不同版本，用前述方法，分别对高、低分辨率情况下的同样画面进行了10人次的找点试验，绘制出不同分辨率下的误差带，通过图11可以看出，两段不同分辨率下的跟踪误差带类似，误差带宽度均值分别为1.09 km/h和1.01 km/h，由此得出结论：图像分辨率对计算误差有一定影响，但影响不显著。

图11 不同分辨率下的误差带

4 结论

在各类客观因素中，视频图像的清晰度直接影响目标车辆特征点的定位精度，是决定计算误差的最关键因素，对于图像模糊的视频资料，只能通过加大计算次数，获得均值从而尽可能逼近真值；

目标车辆距摄像头的距离是影响计算误差的主要因素。目标车辆距摄像头的距离近，画面中一个标尺内的像素数多，找点误差造成的相对误差小；目标车辆距摄像头的距离远，画面中一个标尺内的像素数少，找点误差造成的相对误差大。

分辨率对计算误差有一定影响，目前常用的监控视频的分辩率（704×576）完全能满足交通事故分析及车速鉴定的要求。

跟踪标尺的选取是计算误差的影响因素之一，尽量选取大标尺可以减小计算误差。