面向电力的SDN设备监测研究
程 玮
(厦门海洋职业技术学院,福建 厦门 361100)
近年来,随着计算机网络规模大幅度提升,传统的网络架构已不能满足云计算、服务器虚拟化等新应用的需求。此时,基于传统网络结构的软件定义网络(SDN)应运而生。SDN网络适应了应用的快速变化,但仍然面临着与传统网络相同的问题,即当链路中出现故障时,不能及时准确地进行定位分类。关于故障定位,传统网络研究众多,如荣飞、朱语博等人基于子模块电压分组检测,研究了MMC子模块开路故障诊断定位方法[1];赵建文、李璞等人基于AGM曲线能量,对配电网故障区段定位方法进行了研究[2]。但这些故障定位方法没有考虑到SDN网络结构的特性,因此并不适用于SDN网络链路的故障定位。为此,本研究探讨了一种基于CNN−SVM的SDN网络链路故障定位算法,并从多角度对算法进行了评估。
1 系统框架
根据研究的目的,采集并处理控制器数据以及对定位应用层中的故障,将SDN网络链路故障定位系统设计如图1所示。SDN系统主要由数据层、控制层、应用层、MySQL数据库组成[3]。

图1 SDN网络链路故障定位系统框架
控制层主要的功能是接收来自数据层的带宽、时延等数据[4],并将其存入MySQL数据库中。通常情况下,这些数据不能通过OpenFlow协议直接获得,因此需要通过计算或自行测量等方式获得。
应用层包括数据预处理、模型训练、故障定位等子模块[5]。首先,从MySQL数据库中读取数据,并对数据进行重构、预处理。然后将处理后的数据输入模型,应用卷积神经网络(CNN)和SVM分类器进行训练。最后通过特征提取和故障定位分类,实现故障诊断。
2 基本算法
2.1 CNN-SVM算法
根据系统整体架构可知,传统CNN算法控制层采集的数据虽然可组成二维数组,但它无法提取到不同网络链路间的数据空间相关性,不适用于SDN网络链路故障定位,因此还需对该结构进行改进。本研究在此基础上,提出一种基于CNN−SVM算法的SDN网络链路故障定位模型,其结构如图2所示。该模型主要包括数据输入层、特征提取层、softmax函数层、SVM分类层四个部分[6],一方面可解决传统CNN网络无法提取不同链路的数据空间相关性,另一方面利用SVM算法提高了故障定位的正确率。

图2 CNN-SVM算法模型
2.2 CNN-SVM算法结构
2.2.1 数据输入层
数据输入层主要功能是接收和处理SDN网络底层的原始监测数据[7]。由于CNN模型只能接收二维或三维数据,因此这些数据一般不能直接应用于CNN模型中,故需要对它们进行转化。本研究将一定长度的时间窗口和同一时间窗口中检测到的网络数据构成为图像数据,以便于输入CNN模型。
2.2.2 特征提取层
特征提取层包括激活层、卷积层和池化层,是整个模型的核心组成部分[8]。其中,卷积层主要是通过卷积核提取局部向量的时空相关特征,而卷积核又通过输入数据的结构改变移动方向,实现卷积提取操作,具体如图3所示。

图3 卷积详细过程
令SDN网络链路中K个间隔时间内某一时刻采集到J=Nlinks+Nstatus个监测数据。其中,Nlinks链路数目,Nstatus表示每条链路上的数据个数。那么,CNN−SVM算法可通过K*J个节点的输入层接收SDN网络底层的原始监测数据。由此可得,特征映射中节点的输入值:

式中,Rr和Rs分别表示卷积核的行大小和步长。由于CNN−SVM算法CNN结构中可接收的是标准二维特征映射,而上述操作通过卷积核得到的局部特征为一维特征映射,因此需要在接下来的池化层中使用P*1的池化器沿卷积核时间轴移动方向进行降维处理。
2.2.3 Softmax函数层
传统CNN模型中,全连接层输出的值一般不符合概率分布[9],因此本研究引入Softmax函数层以解决该问题。令模型训练输入样本为x,其对应标签为yˉ;n个类别。则x被分为j类的概率可表示为P(y+j|x);模型具有n个量化的概率值。将n个概率值输入Softmax函数层,应用式(2)可得到一个符合概率分布的n维向量。

式中,Y′i表示Softmax函数对样本i进行处理后的输出值,其取值范围[0,1];P(yi=n|xi)表示样本i属于n类的概率。将Softmax函数分类结果与样本实际标签进行比较,可得出模型的损失误差。本研究中,由于CNN−SVN算法的输入标签为分类标签,故决定采用交叉熵损失函数。交叉熵损失函数的定义如下式(3)所示。

式中,i表示第i个样本,j表示n个分类中第j个分类;表示第i样本的实际标签。通过不断调整式中参数,可使损失函数L(w)值最小。
2.2.4 SVM分类器
SVM分类器是一种用于处理多分类、高维模式识别等问题的经典二多分类模型[10],其模型结构如图4所示。SVM分类器主要由hinge损失和核技巧两个部分组成,其中核技巧包括线性核和非线性核。本研究采用非线性核作为SVM分类器的核技巧,并以非线性SVM分类器作为CNN−SVM算法的分类器,以解决非线性的多分类问题。

图4 SVM模型结构
假设训练集为J={(X1,y1),...,(Xi,yi),...,(Xn,yn)},Xi(Xi∈χ=Rn)表示第i个输入的特征向量,yi=(yi∈ψ={+1,−1})表示xi的分类标签。一般而言,SDN网络底层采集到的故障数据为线性不可分,因此根据式(5)向训练集中引入松弛变量ξi,即可将该线性不可分的问题转化为软间隔最大化的问题。
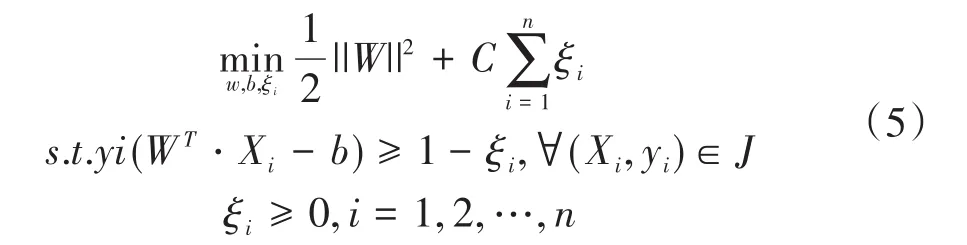
式中,W、b均表示为训练参数;C表示惩罚因子。一个样本对应一个松弛变量,一个松弛变量即为一个hinge损失函数:
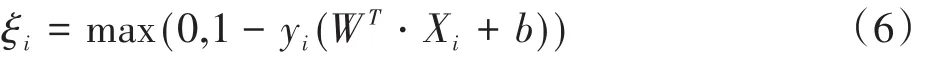
通过不断调节W、b可以使目标函数最小化。然后选择适当的惩罚因子以及核函数,利用拉格朗日乘子法可求解式(5)的对偶问题,得到W的最优解W*。最后通过W*分量wi*计算b的最优解b*:

式中,k(⋅,⋅)为核函数。在线性可分中,核函数可由样本实例的之间的内积进行表示;在线性不可分问题中,首先需要将线性不可分转化为线性可分,通过SVM将样本空间映射到一个高纬度的特征空间,获得了样本在这个特征空间的线性可分,再求得样本实例之间的内积用以表示核函数。但由于特征空间维度较高,因此直接计算内积十分困难。为避免该问题,本研究用决定用非线性SVM核函数替换线性SVM的内积。
设输入空间为□,□*□的对称函数为k(⋅,⋅),则 k为核函数对于任意数据D={X1,X2,…,Xn},核矩阵K总是半正定:

实际上,每一个核函数对于任意输入空间的(Xi,Xj)均存在一个从输入空间到特征空间的映射φ(□)使k(Xi,Xj)满足条件:

常用的核函数主要包括高斯核、多项式核、拉普拉斯核、sigmoid核等,由于高斯核更具有普适性,因此本研究采用高斯核作为SVM的核函数。
3 基于CNN-SVM的SDN网络链路故障定位算法
基于CNN−SVM的SDN网络链路故障定位算法避免了人工提取特征的误差性,使SDN网络链路故障定位更加精确,其故障定位主要分为三个步骤,如图5所示。

图5 基于CNN-SVM的SDN网络链路定位算法流程
步骤1:训练CNN模型。对采集到的SDN网络状态数据进行重构和预处理操作,将处理后的数据作为输入数据。然后利用softmax函数和反向传播算法训练CNN模型,得到最小化损失函数,完成对CNN模型的训练。
步骤2:训练SVM。使用训练好的CNN模型提取原始数据中具有代表性的特征,实现对SVM的训练。
步骤3:故障定位。利用训练好的CNN−SVM对SDN网络链路进行故障定位。
3.2 基于CNN-SVMSDN网络链路状态基本参数
SDN网络中存在多条链路,而这些链路可能同时出现故障。因此,为使CNN−SVM算法可同时定位多条链路故障,应确保控制器采集到的数据能全面反映网络中所有链路的状态。通常情况下,反映网络链路状态的参数众多,包括链路时延、链路吞吐量、链路丢包率等,只有综合利用这些参数,才能更准确地对SDN网络链路状态进行判断。这些参数一般不能由SDN控制器直接获取,需要通过数据计算获取。
4 仿真实验
为验证提出的基于CNN−SVM的SDN链路故障定位算法的有效性,本研究在pycharm中,采用Python从超参数对模型的影响、模型故障定位结果两个方面完成了对CNN−SVM的SDN链路故障定位算法的仿真实验,并通过与标准CNN模型比较,对提出的算法性能进行了分析。
4.1 CNN超参数对模型的影响
CNN是本研究提出的基于CNN−SVM的SDN链路故障定位算法的特征提取部分,因此其超参数对特征提取结果的影响,直接影响整个CNN−SVM故障定位算法的准确度。为使实验参数设置合理,本研究以最小损失函数和softmax函数作为分类函数,探究了除CNN结构(如表1所示)以外的其他超参数,包括激活函数、优化算法、批处理大小对CNN模型的影响。

表1 本实验采用的CNN结构参数
4.1.1 激活函数对模型的影响
常见的激活函数包括sigmoid、tanh、relu,一定程度上影响了CNN模型的训练效果。通常情况下,这些激活函数由历史经验获取,缺乏可靠性。因此本研究在实验中,以批处理大小为100,迭代次数为500,优化算法为Adam对以上常见激活函数进行了比较,得到如表2所示的实验结果。由表可知,在训练时间为135 s左右,tanh函数的训练准确度最高,达到95.89%;relu函数的测试准确度最高,达到95.01%。由此可以看出,relu函数的泛化性更高,故本研究采用relu函数作为CNN的激活函数。

表2 常见激活函数实验结果比较
4.1.2 优化算法对模型的影响
研究以批处理大小为100,迭代次数为500,激活函数为relu的条件下,采用常见的优化算法包括SGD、Adagarad、Adam、AdaDelta对模型训练进行了比较,得到如下表3所示的实验结果。由表可知,Adam优化算法无论是训练时间、测试时间,还是训练准确率或测试准确率均由于其他优化算法,因此本研究采用Adam作为CNN模型的优化算法。

表3 常见优化算法实验结果比较
4.1.3 不同批处理大小对模型的影响
研究以迭代次数为500,激活函数为relu,Adam为优化算法的条件下,通过实验研究了不同批处理大小对模型的影响,实验结果如下表4所示。由表可知,随着批处理大小增大,模型的平均训练时间逐渐缩短,模型的训练准确率先增后减,在批处理大小为64时,模型的训练准确率逐渐降低。因此,综合考虑训练时间和训练准确率,本研究认为批处理大小为64时,可得到最优的模型训练结果。

表4 不同批处理大小对模型训练的影响结果
综上可确定CNN−SVM故障定位算法模型中CNN的部分超参数,其中,激活函数为rulu,优化算法为Adam,批处理大小为64。
4.2 模型故障定位结果与分析
完成上述CNN模型训练后,将CNN全连接层的输出输入SVM中并进行训练,然后将训练好的CNN−SVM模型对SDN网路链路中的故障进行定位。本次实验通过网格搜索确定了惩罚因子和gamma参数分别为10和0.1,以径向基函数作为SVM的核函数,对基于CNN−SVM的SDN网路链路故障定位算法的查准率p、查全率r、F1−测度通过式(11)进行了计算,得到表5所示的计算结果。由表5可知,本研究提出的CNN−SVM算法的查准率、查全率、F1−测度均高于93%,说明该算法基本可满足SDN网络链路故障定位。


表5 CNN-SVM算法的查准率p、查全率r、F1-测度
为更好地分析CNN−SVM算法的漏报、误报率,本研究将表5中8种故障情况,每种故障情况有300个测试样本,共2 400个测试样本的故障定位结果进行了整理,得到如下图6所示的多类混淆矩阵。图6中,横行表示查全率相关信息,竖列表示查准率相关信息,对角线上数据则表示每种故障正确分类的样本数。由图可知,在所有测试样本中,有2 318个故障定位诊断正确,准确率约为96.58%,说明本研究提出的CNN−SVM算法具有良好的故障定位性能,可同时定位SDN网络中多条链路的故障问题。此外,图中链路的故障数目对算法诊断的效果并没有太大影响,这说明本研究提出的CNN−SVM算法的故障诊断性能不会明显受到故障数目的影响。

图6 多类混淆矩阵结果
4.3 算法比较
为探究CNN−SVM算法模型的优势,本研究在激活函数为rulu,优化算法为Adam,批处理大小为64的相同条件下,将该算法模型与标准CNN算法模型(卷积核大小为3*3,池化核为2*2,分类函数为softmax)进行比较。
CNN−SVM算法模型与标准CNN算法模型的训练时间、测试时间、测试准确率的比较结果如下表6所示。由表可知,CNN−SVM算法模型的训练时间和测试时间均低于标准的CNN模型,且其准确率更高,说明本研究提出的CNN−SVM提高了算法故障定位的性能。

表6 CNN-SVM模型与标准CNN模型性能比较
CNN−SVM算法模型与标准CNN算法模型的查准率、查全率、F1−测度比较结果如下图7、8、9所示。由图可知,CNN−SVM算法模型在查准率、查全率和F1−测度方面均优于标准CNN模型,说明CNN−SVM算法模型具有更好的故障分类和定位的能力。

图7 CNN-SVM与标准CNN查准率比较图

图8 CNN-SVM与标准CNN查全率比较图

图9 CNN-SVM与标准CNN的F1-测度比较图
5 结语
本研究根据SDN网络系统结构特点,在标准的CNN算法和SVM分类器基础上,提出一种基于CNN−SVM的SDN网络链路故障定位算法模型。在该模型中,以CNN作为故障数据的特征提取器,以SVM分类器作为故障的定位分类器,实现了对SDN网络链路的故障定位。然后。最后,为提出的CNN−SVM算法的有效性,本研究设计了相关的实验。实验结果表明,本研究提出的CNN−SVM提高了传统CNN算法在SDN网络链路中的故障定位的精确度,具有良好的故障分类和定位的能力。

