基于似然函数的双曲调频信号参数估计快速算法
马碧云 元达鹏 刘娇蛟*
①(华南理工大学电子与信息学院 广州510640)
②(自然资源部海洋环境探测技术与应用重点实验室 广州510300)
1 引言
线性调频(Liner Frequency Modulation,LFM)信号被广泛地应用于雷达侦查、地震勘测、水声通信与仿生声呐等领域,而能否准确地估计出接收信号的参数,将直接影响探测精度,所以对LFM信号的参数估计是一个近年来比较重要的研究方向,国内外学者也作了深入广泛的研究[1–5]。然而在水声环境等复杂的应用场景中,物体间的相对运动会造成多普勒效应,这种多普勒效应不仅会影响接收信号的脉冲压缩结果,也会影响接收信号的参数估计结果,因此LFM信号难以适应此类动态场景的需求。有鉴于此,研究者引入了双曲调频(Hyperbolic Frequency Modulation,HFM)信号。HFM信号不仅具有良好的脉冲压缩性能,还具有多普勒不变性[6],即经过多普勒效应影响的接收信号仍可与匹配滤波器匹配,因此HFM信号近年来在水声等多普勒影响严重的应用领域中得到了广泛的研究,但是目前针对HFM信号参数估计问题的研究较为有限[7,8]。在参数估计问题上,最大似然估计由于其自身估计算法的精度极高,受到广大研究学者的推崇,然而最大似然估计涉及多维搜索的过程,存在因计算量大而无法直接在实际工程中使用的问题。因此本文针对HFM信号,提出一种基于似然函数的HFM信号参数估计快速方法。
本文安排如下:第1节叙述HFM信号以及其参数估计问题的研究背景以及应用意义;第2,3节将介绍HFM信号的特征,并推导HFM信号参数估计的Cramer-Rao下界,作为本文参数估计方法的性能评估标准;第4,5节将基于噪声的高斯随机过程,构建HFM信号的似然函数,利用GABC算法对似然函数进行全局最优化搜索,并针对算法的优化过程,提出一种改进的适应度函数;第6节将通过蒙特卡洛试验验证本文所述方法的有效性,结果表明本方法在保证估计精度的同时能提高算法收敛速度。
2 HFM信号

可见式(2)是关于时间t的双曲函数,因此称为双曲调频信号。
另外,HFM信号的多普勒不变性表现为:经过多普勒效应影响的HFM信号除了存在一个时域上的时间偏移 ∆t外,并不会产生多普勒频移,且其瞬时频率仍然保持相同的调频率k与初始频率f0,因此仍可与匹配滤波器完全匹配[9],上述结果可表示为

式中,fH(t)为 原HFM信号的瞬时频率,fDH(t)为HFM信号经过多普勒效应影响后的瞬时频率,时间偏移∆t=(1−α)/αkf0,其中α为多普勒尺度因子。
因此相比于LFM信号,HFM信号具有多普勒不变性,经多普勒尺度变化后的信号参数仍保持不变,在复杂水声环境中的信号参数估计问题上具有一定优势。
3 高斯白噪声下的Cramer-Rao下界
在参数估计问题中,Cramer-Rao下界为任意无偏估计量的方差确定下界,即无偏估计量的方差只能无限逼近Cramer-Rao下界,但不会小于该下界[10]。因此,本节通过推导Cramer-Rao下界,为任意无偏估计量的性能比较提供了一个参考标准。
在高斯白噪声环境下,采样所得的HFM信号服从高斯随机过程


4 HFM信号的似然函数
HFM信号参数的最大似然估计为渐近无偏估计,在理论上最大似然估计可以逼近Cramer-Rao下界,具有极高的估计精度。

其中,fs为采样频率;w(n),n∈{1 2···M}为零均值的复高斯白噪声随机过程,其实部与虚部方差均为常量σ2,且相互独立;其中调频率k与初始频率f0的最大似然估计值为HFM信号参数估计的最终目的。
为了方便化简,式(12)可表示为向量形式



5 似然函数优化问题
传统的最优化算法如牛顿迭代法、最速下降法、共轭梯度法等,由于对目标函数有着较高要求,比如要求目标函数必须可导,因此在大多数实际问题中无法使用。近年来,仿生智能优化算法因其对复杂问题具有高效的优化性能且无需目标函数导数信息等优点,受到研究学者的广泛关注。在最优化算法的搜索过程中,均需要通过反复计算适应度函数值进行个体筛选,因此适应度函数的选取将直接决定算法的收敛速度以及能否寻得最优解。有鉴于此,本文根据最优化算法的搜索过程改进了其中的适应度函数,使得最优化算法在保证准确性的同时降低一定的计算量。
5.1 最优化算法
随着1975年遗传算法(Genetic Algorithms,GA)的提出,经过几十年的发展,研究学者针对不同的应用问题提出了多种仿生智能算法,各种方法因适用范围不同,都有一定的优缺点,需要根据实际的问题进行选择应用。
Karaboga等人[12]于2007年提出人工蜂群(Artificial Bee Colony,ABC)算法用于解决多变量函数优化问题,后来Zhu等人[13]提出全局最优引导的人工蜂群算法(Global best-guided Artificial Bee Colony algorithm,GABC),它的基本思想是将每个蜜源位置表示为待求问题的一个可行解,并通过模仿蜜蜂采蜜行为来进行最优解搜索。GABC算法在多维函数优化问题上表现优秀,且具有鲁棒性强、控制参数较少等优点。相比于ABC算法,GABC算法通过跟随当前最优值进行搜索,优化结果精度更高。因此针对似然函数的优化问题,本文选择GABC算法作为下文研究HFM信号参数估计问题的最优化算法。
5.2 时间复杂度分析
在优化过程中,最优化算法无一例外地需要在每一次迭代中,对适应度函数进行与个体数量同等次数的计算,以得到所在位置参数下的适应度大小,因此不同最优化算法的时间复杂度如表1所示。
其中最大似然估计中的D为待估计参数的总数,u j与lj分别是第j个参数的搜索范围上界与下界,p j为第j个 参数的遍历精度;CGA,CABC,CGABC分别为GA算法、ABC算法、GABC算法的个体数量,NGA,NABC,NGABC分别为GA算法,ABC算法,GABC算法的最大迭代次数,Tfit为适应度函数的时间复杂度。
由表1可以看出,适应度函数的复杂度是最优化算法整体复杂度的主要组成部分,因此适应度函数的设计需要尽可能简单,使得整体算法的时间复杂度最小。
5.3 适应度函数的优化
在最优化算法中,优化过程正是对解成员进行“优胜劣汰”的过程,而解成员的好坏由它的适应度函数值所决定,因此适应度函数的选取将直接决定算法的收敛速度以及能否寻得最优解。
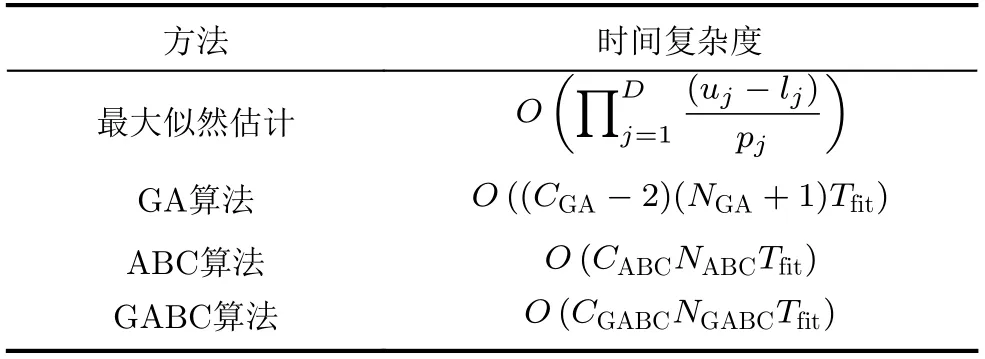
表1 不同方法的时间复杂度
对于HFM信号的参数估计问题,传统的适应度函数为压缩概率函数[14],即蜜源个体mi的适应度fiti(m i)为

然而若采用式(24)作为适应度函数,每次计算都将涉及矩阵取逆的高复杂度操作;并且由于参数(k i,f0,i)在优化过程中是随机选取,因此存在SH(k i,f0,i)S(k i,f0,i)矩阵不可逆的可能性;此外在部分最优化算法(如ABC算法、GABC算法)中,涉及同时对多个个体进行适应度计算,而式(24)的每次计算只能得到单个个体的适应度,缺乏并行计算能力。

使用式(25)作为最优化算法的适应度函数计算公式,不仅避免了式(24)复杂的矩阵求逆运算,以及存在矩阵不可逆而导致的精度下降,且避免通过低效率的循环去计算多个个体[m1m2···m C]的适应度值,从而提升了最优算法的整体收敛速度。
6 实验验证
实验1:适应度函数的有效性验证
由于最优化算法是通过不断比较适应度函数值的大小进行优化搜索,因此适应度函数的有效性需要首先得到验证,即通过对适应度函数进行优化搜索能得到正确的参数估计值。图1分别为适应度函数式(24)与优化后的适应度函数式(25)在不同参数组合下的2维遍历,其中HFM信号的初始频率f0为1.5 MHz,调频率k为–0.077802。
如图1(a)所示,当适应度函数取得最大值时,横纵坐标所代表的参数估计值与初始设定值相同。其中纵轴为待估计HFM信号的初始频率,横轴表示待估计HFM信号的调频率。而相比于图1(a),图1(b)虽在部分有一定的隆起,但在该适应度函数取得最大值时,横纵坐标所代表的参数估计值也与初始设定值相同,满足作为适应度函数的条件。
实验2:估计值的均方误差与Cramer-Rao下界对比
本文通过1000次蒙特卡洛仿真试验,对比了多种参数估计方法在HFM信号参数估计问题中的性能。在优化算法的参数设置如下:在GA算法中,令种群大小为40,最大遗传代数为1000,个体长度为20,代沟为0.95,交叉概率为0.7,变异概率为0.01;在ABC算法中,蜂群群落大小为60,最大迭代次数为1000;在GABC算法中,蜂群群落大小为80,最大迭代次数为100;在最大似然估计法中,f0的遍历精度为50 Hz;k 的遍历精度为 1 ×10−5。

图1 不同适应度函数的2维遍历结果
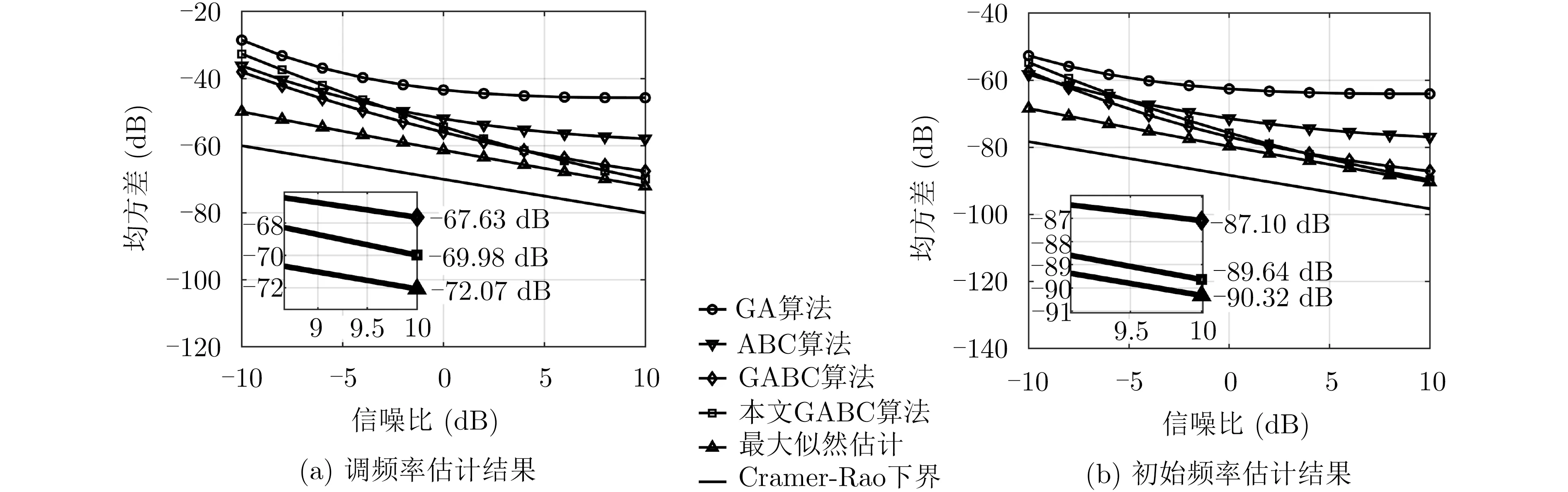
图2 不同方法下估计参数的均方误差与Cramer-Rao下界
图2为在–10~10 d B信噪比内多种参数估计方法的性能比较。如图2所示,5种估计方法的均方误差都随着信噪比的增加,总体呈现下降的趋势:其中最大似然估计的性能最优,均方误差可随着搜索精度的提升而逼近Cramer-Rao下界;对于GA算法,在信噪比达到0 d B以上时,受信噪比的影响将减小,均方误差的变化将趋于平缓;与ABC算法而言,由于问题针对性较强,因此其估计结果的均方误差小于GA算法,但仍与最大似然估计的性能有明显差距;相比之下,GABC算法由于引入了全局最优引导项,因此其估计结果的精度更高,均方误差能随着信噪比的增加而逼近Cramer-Rao下界。
另外从图中可知,标准GABC算法相比于采用优化后的适应度函数式(25)的GABC算法,前者存在矩阵不可逆的可能性,因此两曲线在图中没有完全重合,但总体性能相差不大;在信噪比为4 dB以上时,后者的均方误差更接近于最大似然估计的性能。而在信噪比为10 d B时,对于参数k和f0,与最大似然估计的均方误差相比,前者相差分别为4.44 d B与3.22 d B,而后者分别相差2.09 d B与0.68 d B,后者更接近最大似然估计的性能。在水下应用中由于噪声水平不高,信噪比大致保持在5 dB以上,因此文中所述方法能被有效地用于HFM信号的参数估计问题中。
实验3:收敛速度对比
在完成有效性的验证后,下面对比GABC算法、与采用优化后的适应度函数式(25)的GABC算法在HFM信号参数估计问题中的收敛速度以及算法耗时,其中两种GABC算法的参数设置均相同,蜂群群落大小为20,最大迭代次数为80。
如图3所示,GABC算法和采用优化后的适应度函数式(25)的GABC算法均能在50次迭代内寻得最优值,虽然后者收敛速度稍快,但总体相差不大。因此可以预见的是,在相同的迭代次数内,适应度函数的时间复杂度越低,GABC算法的实现效率就越高。
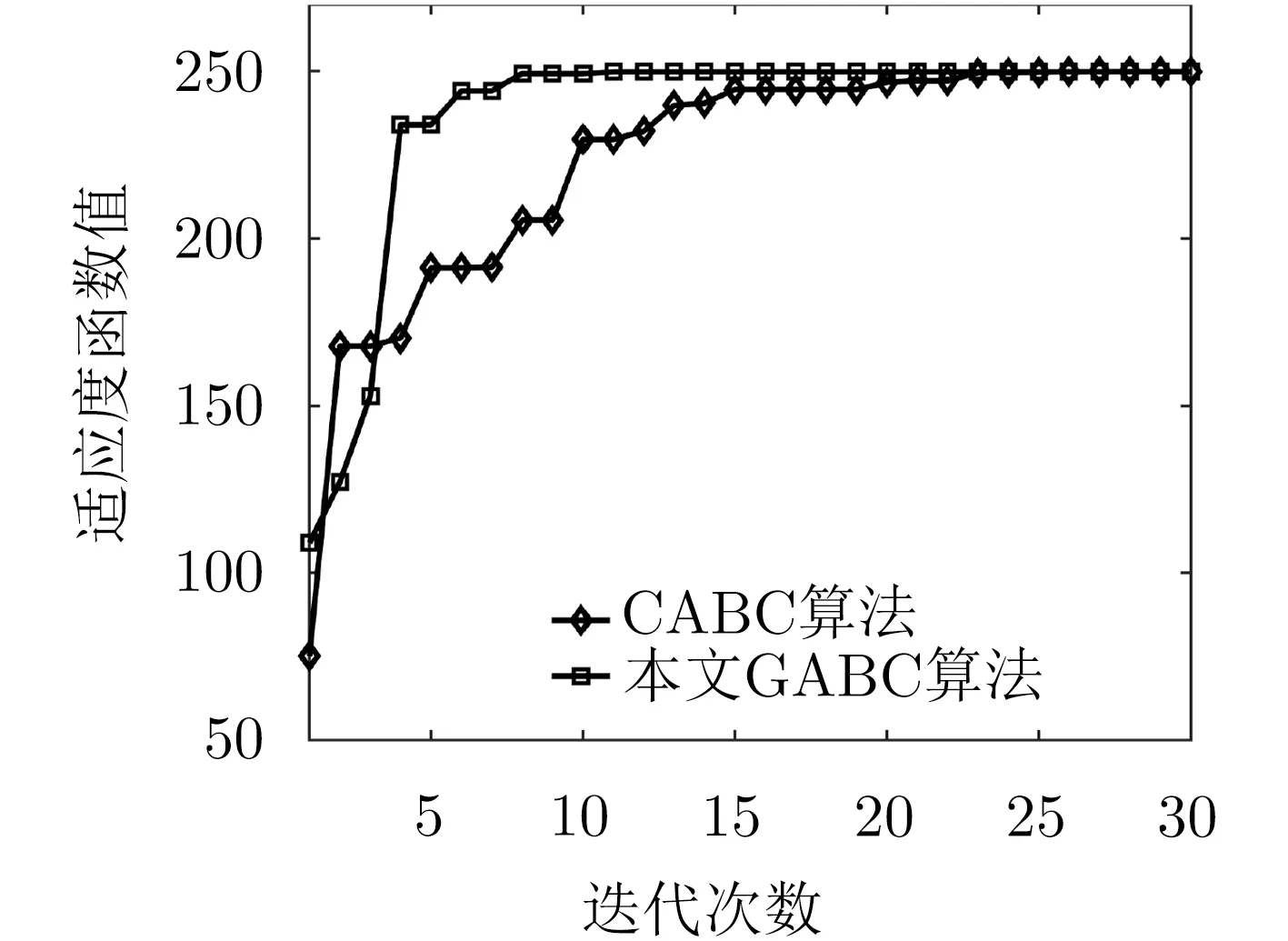
图3 基于不同适应度函数的GABC算法收敛速度
因此本文通过Matlab中的探查器(Profile)可得算法的时间消耗,即最大似然估计的时间消耗为13738.8 s,GABC算法的时间消耗为1.785 s,适应度函数优化后的GABC算法的时间消耗为0.715 s。可见针对HFM信号的参数估计问题,采用本文提出的适应度函数式(25)的GABC算法在具有较高精准度的同时,也具有较快的收敛速度。
7 总结
本文首先推导出HFM信号参数估计的Cramer-Rao下界,作为本文参数估计性能的评估标准。然后基于高斯随机噪声,构建了HFM信号的似然函数,并结合数据向量化的特点提出一种改进的适应度函数,最后利用GABC算法对该适应度函数进行极值寻优,从而实现HFM信号的参数估计;通过蒙特卡洛仿真证明了本方法在信噪比为3 d B以上时,HFM信号的参数估计结果的均方误差更逼近Cramer-Rao下界,且运算量约是原来的1/3。

