利用计算机研究单层保温对管道散热的影响
吕慧敏,刘新状
(中国电子工程设计院有限公司)
1 引言
管道保温的主要目的是减少热量损失,防止管道内的热介质凝结;减少锅炉提供的热量,降低燃料消耗,达到节能目的。
目前,在工程设计中主要采用经济保温层厚度方法,但是该方法受设计保温层运行年数、热量的价格和保温材料的年分摊费用等多种因素的影响,由于这些因素在不同的时间段内存在变数,所以经济保温层厚度会发生变化。运行时,上述因素发生变化,那么当下的经济保温层厚度就不是设计时的经济保温层厚度。由于存在变数,文章不采用经济保温层厚度方法进行研究,直接研究散热量与保温层厚度的关系。
管道的排布方式不同,管道保温层散热损失的计算方法不同,由于实际中水平管道占比非常大,所以文章只研究水平管道的保温层厚度对散热的影响。管道输送过程中热介质在管道内部,因此其散热的过程为:热量由管道内部传热到管道外表面(文章研究的是金属管道,因此该部分的热阻非常小,所以不考虑该部分热阻),再由管道外表面传热到保温层的外表面,再通过保温层的外表面对流和辐射传热到环境中,多层保温的计算与单层保温计算类似,所以本文只用单层保温为例进行研究。该过程需要分上述两部分(对流传热和辐射传热)进行计算。具体单层保温散热量公式如下[1]:
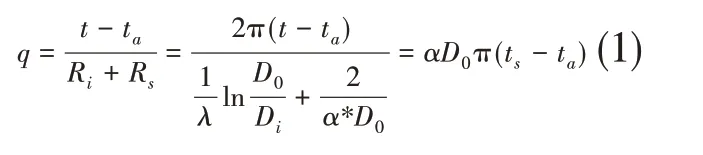
其中:t,ta,ts分别为管道的外表面、环境、外表面温度℃;Ri为隔热层热阻,m·K/W;Rs为隔热层表面热阻,m·K/W;α为隔热层外表面向大气的放热系数,W/m2·℃;q为单位表面热损失量,W/m;D0为隔热层外直径,m;Di为隔热层内直径,m;λ为隔热层材料制品的导热系数,W/m2·℃.
上述隔热层外表面的放热系数α是辐射放热系数αr和对流放热系数αc的综合值。即:
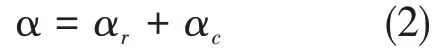
αr为辐射放热系数,W/m2·℃;αc为对流放热系数,W/m2·℃;α为表面放热系数,W/m2·℃。
当管道敷设情况比较复杂,要求精确计算时,可按JISA9501规定计算。
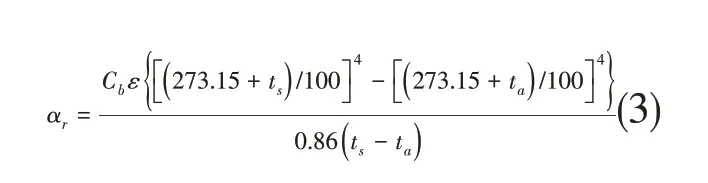
Cb为完全黑体的辐射常数4.88;ts为表面温度,℃;ta为环境温度,℃;ε为镀锌板为0.5。

Vm风速m/s。
保温材料的导热系数λ:
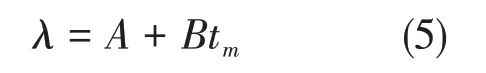
A,B是不同材质的保温材料系数;tm为平均温度,℃。
其中tm:
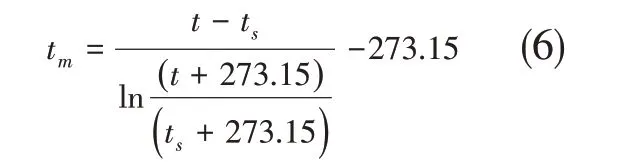
符号的意义与上面相同。
将公式(3),(4),(5)代入公式(1),得到的方程式中,未知的只有管道外表面温度ts,要求出管道外表面温度,通过人工计算,该过程非常困难,所以采用计算机对该方程进行求解。
以岩棉保温壳为保温材料,其导热系数方程为0.040+0.0002tm[1],计算达到的精度要求为0.000001,以内部管道的表面温度350℃、环境温度15℃、风速2.0m/s、管道直径350mm为参数,对管道的表面温度和散热量进行计算[2]。
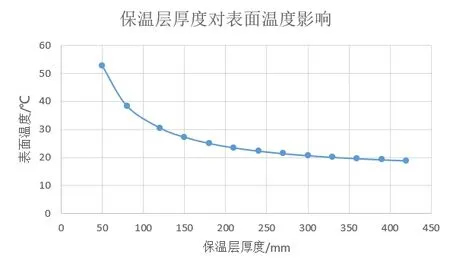
图1 保温层厚度对管道外表面温度影响
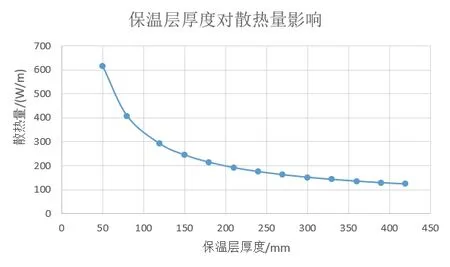
图2 保温层厚度对管道散热量的影响

图3 风速对保温层外表面温度影响

图4 风速对保温散热量的影响
2 探讨保温层厚度对表面温度和散热量的影响
当不同的保温层厚度时,其对管道散热量和管道的外表面温度的影响如图1和图2所示。
由图1和图2可知:管道的散热量随着保温层的厚度的增加而明显减小,从散热趋势可以看出,管道由无保温到增加保温,其散热趋势下降比较明显,只要进行保温,其散热量就会明显的减小,尤其当保温层厚度超过200mm后,散热损失明显趋于一个常值,即增加保温层厚度对散热损失的影响很小,所以在保温层的厚度达到一定数值后,其经济性就比较差。管道的外表面温度随着保温层厚度增加而逐渐减小,当达到一定的厚度时,其减小的趋势也比较小。
3 探讨风速对表面温度和散热量的影响

图5 保温散热计算程序界面
保温层厚度为200mm的岩棉保温壳材料,计算精度为0.000001,管道的外表面温度为350℃,环境温度为15℃,管道直径为350mm,以此为例计算风速对保温层外表面和散热量的影响,其影响如图3和图4所示。
由图3和图4可知:在正常保温情况下,风速对散热量的影响较小,对保温层外表面的温度影响也较小,所以在保温合理的情况下,风速对其散热影响很小。
程序界面如图5所示,程序计算简单快捷。
4 结语
由以上分析可知,热管道的散热量受保温层厚度影响较大,尤其是保温层厚度比较薄的情况下,随着保温层厚度的变化其散热量变化很大,当保温层达到一定厚度时,随着保温层厚度的变化其散热量变化不明显;在合理保温层厚度的情况下,风速的变化对散热损失的影响非常小。

