水平荷载作用下群桩效率及影响因素分析
李翻翻, 温广军, 赵华宏, 吴平平*, 张志峰, 谭贤君
(1.安徽省交通规划设计研究总院股份有限公司,工程技术研究院,合肥 230088;2.中国科学院武汉岩土力学研究所,岩土力学与工程国家重点实验室,武汉 430071)
圆截面群桩基础作为常用的基础形式之一,除承受结构自身重力以及行车等产生的竖向荷载外,还会受到桥梁上部结构(如拱桥)、地震等产生的水平荷载[1]。水平荷载与竖向荷载作用下桩-岩/土相互作用形式以及相邻桩间的干涉效应均不相同,因此需针对水平荷载作用下的群桩效应开展相应的研究。
张鹤年等[2]通过对PHC(pre-stressed high-strength concrete)管桩在水平荷载作用下的承载特性进行分析,对影响PHC管桩受力特性的主要影响因素进行讨论,并分析了不同桩型水平荷载作用下的群桩效应。陶学俊等[3]采用三维弹塑性有限元方法,研究了现浇混凝土大直径管桩群桩在水平荷载作用下的工作性状,比较了现浇混凝土大直径管桩群桩和等截面实心圆形桩群桩的水平承载力和群桩效率,得到了现浇混凝土大直径管桩纵、横向群桩效应的临界桩距,同时分析了桩距、桩数及桩顶约束条件对现浇混凝土大直径管桩群桩效率的影响。王健等[4]通过对群桩效应的p-y曲线(p代表水平抗力,y代表水平变位)进行分析,同时总结中外的实验数据,提出了群桩效率相关的经验计算公式。李早[5]假设桩土之间保持弹性接触且不发生分离,建立水平受荷桩的位移控制方程,采用Mindlin解计算土体水平位移传递系数,提出了一种水平受荷刚性承台群桩力学简化分析方法。Modarresi等[6]通过一系列群桩离心模型试验发现密度、桩距及桩顶条件对相邻桩相互作用系数影响显著,并基于测试结果修正了Randolph-Wroth方程,最后将计算结果与有限元分析结果进行比较。Goit等[7]通过不同幅度的动态水平荷载群桩试验对动力学及土体局部非线性对桩-桩干涉效应的影响进行了研究,发现群桩间的共振对干涉效应影响较大,且随着振幅的增加,土体的非线性行为显著,并基于试验结果提出了新的群桩效应系数半经验公式。Isbuga[8]通过建立两根桩的相互作用模型,在考虑桩-土-桩相互作用的基础上修改了桩挠度的控制微分方程,并求解了每个桩挠度的解析解,最后使用Fortran语言编写的有限差分法以数值方式获得每个桩的位移变化,对比结果显示了解析解的可靠性。Ai等[9]使用Bernoulli-Euler梁建立群桩模型,采用间接边界元方法建立了土体模型,同时基于横观各向同性的多层半空间的基本解,推导了桩与横观各向同性多层半空间之间相互作用的控制方程,最后通过数值算例验证了所提出的理论。符羽佳等[10]通过改变桩间距、支部位置、支部数量的模型桩试验与等截面桩试验的对比分析,研究了砂土中高承台支桩的群桩效应。朱小军等[11]通过自行研发的可视化模型试验装置,对砂桩单桩、群桩进行了室内模型试验,并设置了钢管桩单桩对照组,研究了砂桩的荷载-沉降、桩土应力比、沉降-时间及桩土应力比-时间的关系。
水平荷载作用下群桩干涉效应可分为两部分:一部分是桩通过岩土体将部分力直接作用在相邻桩上(直接影响);另一部分是桩通过改变相邻桩后岩土体的应力和位移状态(间接影响)。基于弹性叠加原理,在假设应力扩散角保持恒定的情况下,推导了纵向排列、横向排列以及斜向排列下单桩的群桩效应系数,并基于单桩的群桩效应系数求解了1×2、2×2和3×3排列形式的群桩效率,最后本文分析了桩距与桩径比、弹性模量及泊松比变化对群桩效率的影响,并通过数值法计算的群桩效率与公式法计算结果对比,验证了公式法计算结果的可靠性。
1 群桩效率分析
韩理安[12]中考虑桩与桩之间的影响并按照极限平衡状态推导了水平荷载作用下排桩与群桩的群桩效率公式。该方法并未考虑相邻对桩后岩土体的干涉效应(如图1所示)。下文在文献[12]的基础上考虑相邻桩对桩后岩土体的干涉效应,重新推导了不同组合下的群桩效应系数。(下文中称平行于水平荷载方向的排列方式为纵排,垂直于水平荷载方向的排列方式为横排。)

图1 群桩干涉区域示意图Fig.1 Schematic diagram of pile group interference area
1.1 纵排桩群桩效应系数
作如下假设:①土的应力扩散角恒定;②满足叠加原理;③假设岩土体变形未达到塑性范围。
按照上述假设可将图1中纵排桩的应力分布简化为图2。若忽略前排桩对后排桩的影响,此时后排桩的水平抗力与单桩条件下的水平抗力相同,该水平抗力由桩后岩土体提供。而实际前排桩在水平荷载的作用下会对后排桩的水平抗力产生明显影响,主要分为两部分。
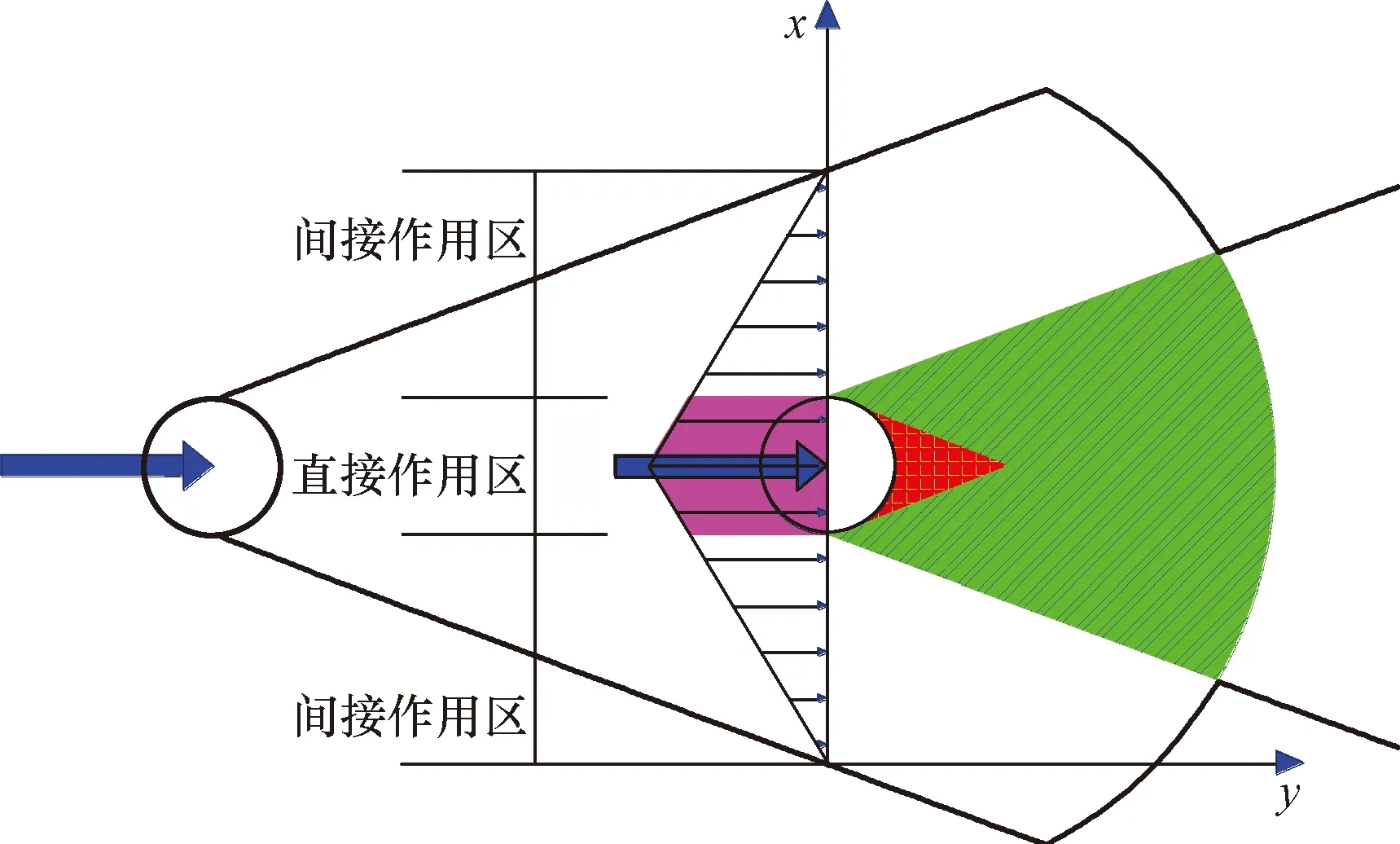
图2 纵排相邻桩间作用关系示意图Fig.2 Schematic diagram of the interaction between adjacent piles arranged longitudinally
(1)前排桩部分荷载通过两桩之间岩土体直接作用于后排桩上(图2中所示直接作用区范围),该部分作用力的大小为图2中粉色区域面积,表达式为
(1)
式(1)中:ΔF1为前排桩通过土体直接传递到后排桩的力;F0为作用于桩上的力;N为桩间距与桩径之比;φ为岩土体的应力扩散角。
(2)前排桩部分荷载(图2中所示间接作用区范围)通过改变后排桩桩后岩土体应力状态,削弱后排桩桩后土抗力,抗力削弱大小与桩间距、桩径以及岩土体物理参数相关,表达式为
ΔF2=F0f1(N,E)
(2)
式(2)中:ΔF2为前排桩间接作用在后排桩的力;f1()为纵排桩间接作用下岩土体抗力削弱程度,其与桩间距、桩径以及岩土体物理参数有关;E为岩土体弹性模量。
因此纵排形式下后排桩的群桩效应系数K1可写成
(3)
实际工程中,群桩受力分配必然不均匀,因此引入不均匀分配系数[12]对式(3)进行修正,可得群桩效应系数为
(4)
式(4)中:α1、β1由N=1时群桩效应最大和N=K1时(纵排桩一般认为K1=8)无群桩效应的条件确定。
1.2 横排桩群桩效应系数
按照前文假设横排桩间影响范围图可简化为图3形式。在不考虑1号桩的影响下,2号桩在水平荷载作用下的岩土体水平抗力与单桩形式下相同。现因1号桩影响了2号桩后岩土体应力状态,降低了其桩后岩土体抗力水平,削弱后排桩桩后土抗力,抗力削弱大小与桩间距、桩径以及岩土体物理参数相关,表达式为
ΔF=F0f2(N,E)
(5)

图3 纵排相邻桩间作用关系示意图Fig.3 Schematic diagram of the interaction between adjacent piles arranged horizontally
则横排桩形势下2号桩的群桩效应系数表达式为
K1=f2(N,E)(α2lgN+β2)
(6)
式(6)中:α2、β2由N=1时群桩效应最大和N=K2(K2代表纵向无群桩效应时N的取值,横排桩一般认为K2=4)时无群桩效应的条件确定。
1.3 斜桩群桩效应系数
如图4所示,当桩处于倾斜位置时,可将桩顶水平荷载分解至平行于桩芯线方向和垂直于桩芯线方向,平行于桩芯线方向的影响系数Kp表达式为
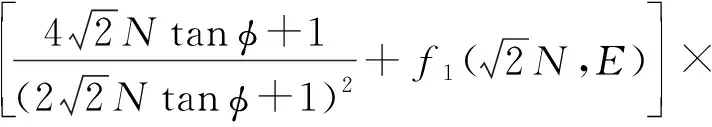
(7)
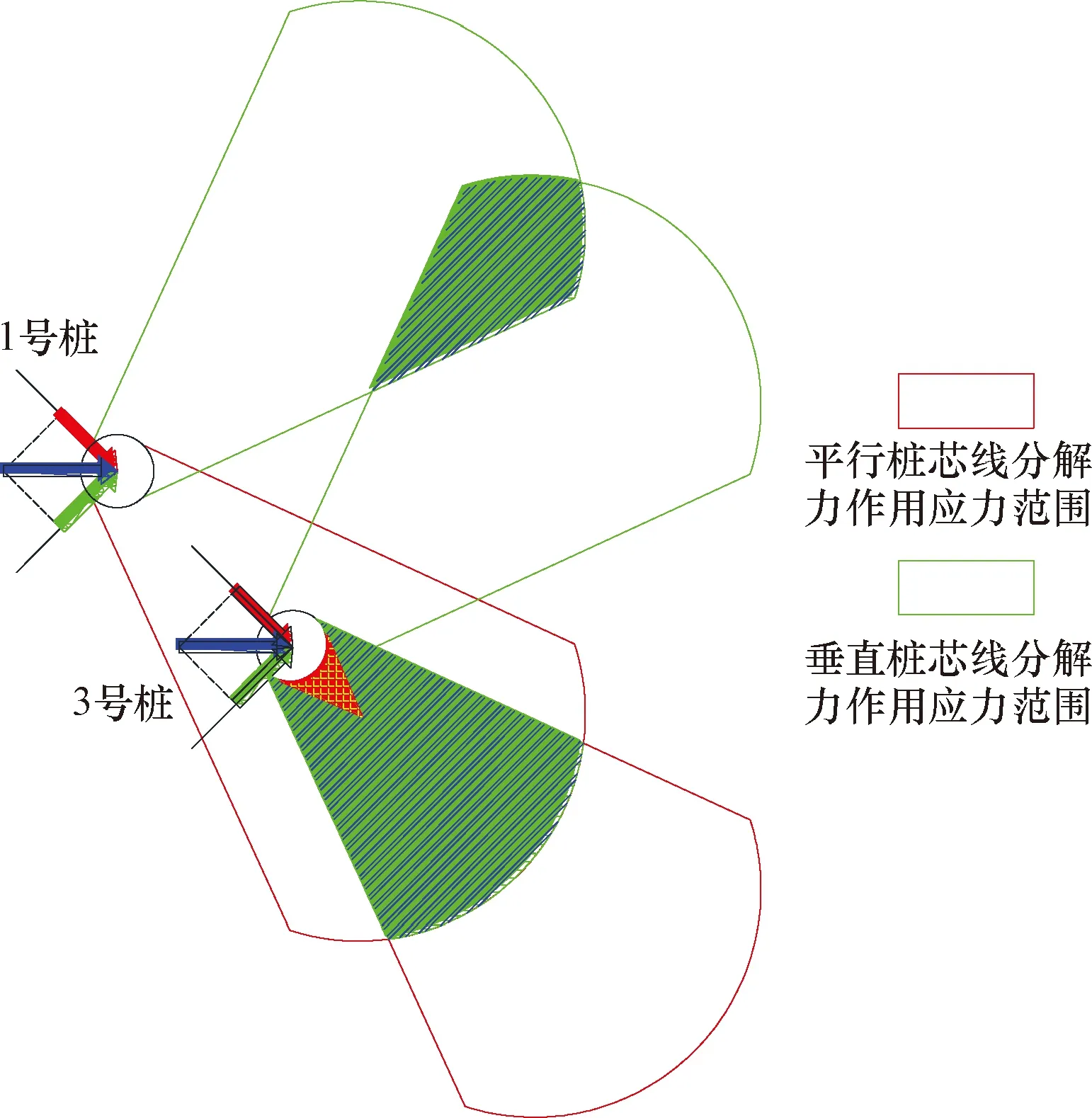
图4 斜排相邻桩间作用关系示意图Fig.4 Schematic diagram of the interaction between adjacent piles arranged diagonally
垂直于桩芯线方向的影响系数Kv表达式为
(8)
则斜桩群桩效应系数K3表达式为
(9)
1.4 不同排列形式下群桩效率
根据前三节分析结果,下文中将给出1×2(纵向排列)、2×2、3×3排列组合形式下的群桩效率,三种形式下桩的排列形式及编号如图5所示。
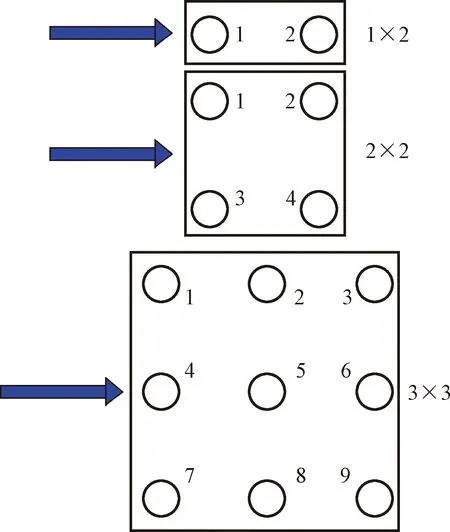
图5 不同排列形式群桩布置形式Fig.5 Arrangement of pile groups in different arrangements
1×2纵向排列形式下群桩效率η1为
(10)
2×2排列形式下群桩效率η2为
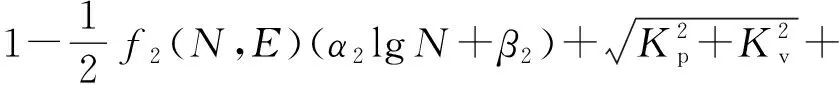
(11)
3×3排列形式下群桩效率η3为

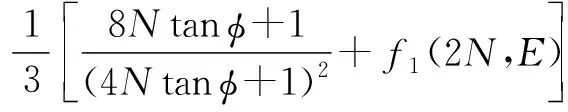
(12)
(13)
(14)

(15)

(16)
1.5 群桩间接作用影响系数
如图6所示,王健等[4]通过总结已有群桩效率结果给出了纵排桩与横排桩的群桩效率随桩距与桩径比的变化规律,从图6中可以看出,随着桩距与桩径比的变大,群桩效率呈负指数或幂函数形式逐渐增大,文献[4]中给出经验表达式为
(17)
式(17)中:βv为横排桩影响系数;βp为纵排桩的影响系数。
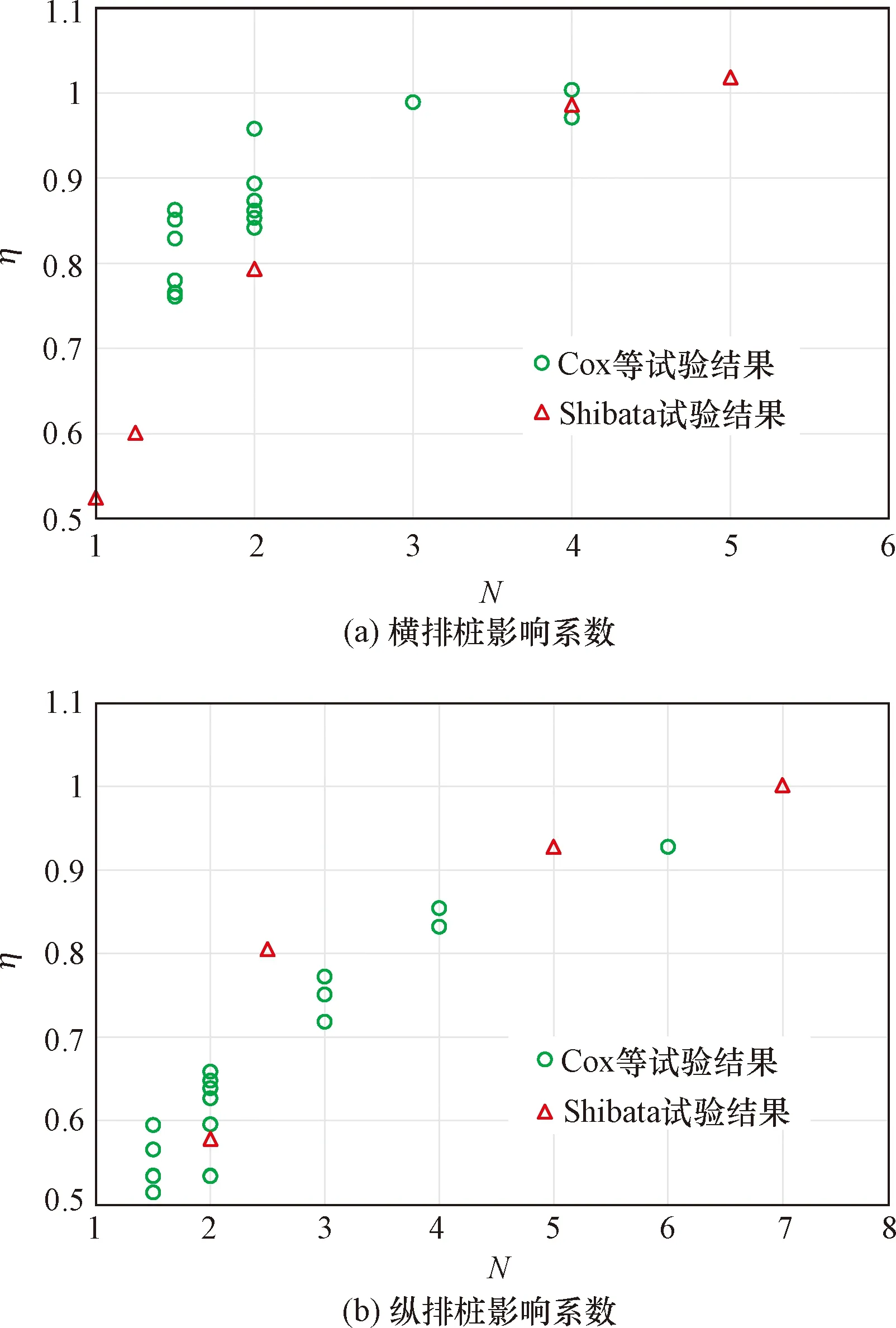
图6 已有纵排及横排桩群桩效率试验结果Fig.6 Existing test results of pile group efficiency of longitudinal and horizontal piles
Modarresi等[6]通过研究发现,群桩间的影响系数还与岩土体的弹性模量有关,因此间接作用下纵排桩和横排桩的影响系数表达式为
(18)
式(18)中:E0=1 MPa;γ1(2)、n1(2)为模型参数,参数结果通过反演文献[4]试验结果获取。
2 群桩效率影响因素分析
主要通过有限元讨论了桩距与桩径比、弹性模量及泊松比对群桩应力场及位移场的影响,确定上述因素对群桩效率的影响,验证上节中群桩效率公式影响因素设置的合理性。选取桩距与桩径比为N=3,岩土体弹性模量E=100 MPa,泊松比ν=0.2为标准情况,对比工况参数选取如表1所示。

表1 对比工况参数设置Table 1 Parameter settings for comparison conditions
群桩桩顶采用固接形式(即有承台),施加相同的水平荷载F=1×106N,单桩尺寸为:桩长20 m,桩径1.5 m。
2.1 桩距与桩径比
Ansys的计算结果显示当N=2时,桩顶水平位移为1.153 mm;当N=8时,桩顶水平位移为0.757 mm,随着N的增大,荷载不变的情况下桩顶水平位移逐渐增大,这是因为N越大,群桩效应越不明显,群桩效率越大,其抵抗水平荷载的能力越强。
图7所示为不同桩距与桩径比情况下(单桩编号沿用图5编号)群桩作用范围内岩土体的位移和应力云图。从图7中可以看出:
(1)N=2时,每根桩桩后岩土体的位移和应力云图因桩与桩之间的干涉效应而呈现出不同的形状,随着N逐渐增大,这种现象越来越不明显,当N=8时,每根桩后岩土体的位移和应力集中区的云图形状已非常相似。这是因为当桩距与桩径比越小,群桩效应越明显,随着桩距与桩径比的增大,群桩效应逐渐减小,当桩距与桩径比达到8时,群桩效应可以忽略不计[3]。
(2)群桩效应显著时,群桩中位于中心位置的桩后岩土体的应力偏小,而位移却偏大。中心桩后岩土体应力偏小是因为群桩中单个桩体越靠近群桩中心位置,群桩效应系数越大,其所分配的荷载越小[12];中心桩后岩土体位移偏大是因为其受相邻桩体的影响最大,在相邻桩的叠加影响下中心桩后岩土体会产生较大位移,这也是中心桩后岩土体所能承受水平荷载偏小的原因。
(3)群桩效应显著时,群桩中位于边侧位置的桩(4、6、7、9号桩)后应力云图形状呈现向外侧延伸,而位移云图形状呈现向内侧延伸。这是因为靠近中心位置群桩效应最明显,中心位置岩土体相较于群桩外侧岩土体抵抗水平荷载能力偏小[12],则边侧位置的水平荷载倾向于向外侧延伸;位移云图形状向内侧延伸也是因为群桩效应在中心位置最明显,在叠加影响下中心位置岩土体水平位移最大,边侧位置桩后岩土体位移云图呈现向内侧延伸。
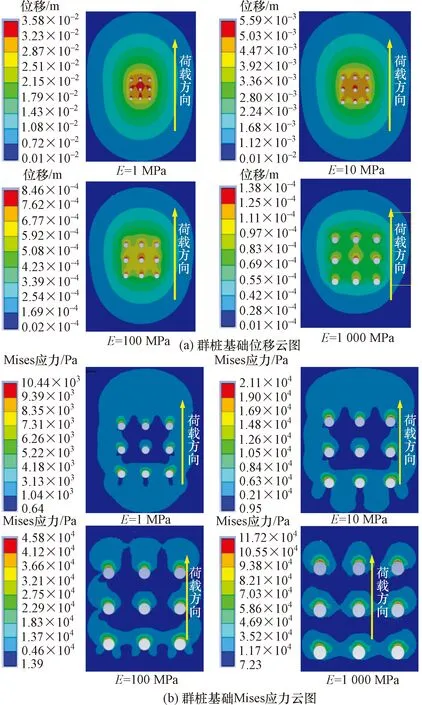
图8 不同弹性模量下群桩作用范围位移和应力云图Fig.8 Displacement and stress cloud diagram of pile group action range under different elastic modulus
2.2 弹性模量
计算结果显示当E=1 000 MPa时,桩顶水平位移为0.201 mm;当E=1 MPa时,桩顶水平位移为37.081 mm。这是因为随着岩土体的弹性模量降低,相同水平荷载下岩土体抵抗变形的能力越弱,桩顶水平位移越大。
图8所示为岩土体在不同弹性模量下,群桩作用范围内岩土体的位移和应力云图。从图8中可以看出:
(1)随着弹性模量的升高,群桩间位移和应力干涉区域逐渐减小。这是因为随着弹性模量的升高,岩土体抵抗水平荷载产生的变形越小,桩与桩之间的干涉效应明显降低,从而使得群桩效应逐渐减小。

图9 不同泊松比下群桩作用范围位移和应力云图Fig.9 Displacement and stress cloud diagrams of pile groups under different Poisson’s ratios
(2)图中出现了与3.1节中(2)和(3)类似的现象。这说明不论弹性模量如何变化,群桩效应最显著的位置依然位于群桩中心。
2.3 泊松比
计算结果显示当ν=0.1时,桩顶水平位移为0.962 mm;当ν=0.4时,桩顶水平位移为1.019 mm,随着泊松比的增大桩顶水平位移也在逐渐增大。这是因为弹性模量保持恒定时,泊松比越大,剪切模量越小,在相同水平荷载下产生的位移越大。
图9中给出了岩土体在不同泊松比下,群桩作用范围内岩土体的位移和应力云图。从图9中可以看出:
(1)随着泊松比的增大,位移云图整体形状逐渐发展为扁平形。这是因为随着泊松比的增大,剪切刚度减小,应力扩散角减小,因此位移云图形状逐渐发展为扁平形。
(2)泊松比变化对桩与桩之间的干涉区域的影响并不明显,通过计算群桩效率发现当ν=0.1时,群桩效率为0.688;当ν=0.4时,群桩效率为0.687,群桩效率变化不明显。因此认为泊松比的变化对群桩效应影响可忽略不计。
综上所述可知:
(1)桩距与桩径比、弹性模量对群桩效应影响显著,表现为桩距与桩径比、弹性模量越大,群桩效应越不明显,而泊松比对群桩效应影响可忽略不计,验证了群桩效率公式中影响因素设置的合理性。
(2)群桩效应最显著的位置位于群桩中心,表现为群桩中心位置的桩后岩土体水平位移大,而所能承受的水平抗力小。
3 群桩效率计算模型数值验证
为验证上述计算模型的准确性,本文通过Ansys建立1×2(纵向排列),2×2及3×3形式的群桩组合平面模型进行有限元分析(如图5所示排列形式),并将有限元分析结果与公式计算结果进行对比验证。
图10所示为不同桩距与桩径比、弹性模量下两种方式计算群桩效率的对比结果,从图中可以看出公式法计算结果与有限元数值模拟结果基本吻合,说明公式法计算结果能很好地反映桩距与桩径比和弹性模量变化对群桩效率的影响。

图10 不同排列形式群桩效率公式法与数值法对比图Fig.10 Comparison chart of formula method and numerical method of pile group efficiency in different arrangements
4 结论
(1)基于弹性叠加原理,在假设应力扩散角恒定的情况下,推导了纵向排列、横向排列以及斜向排列下单桩的群桩效应系数,并基于单桩的群桩效应系数求解了1×2、2×2和3×3排列形式的群桩效率。
(2)通过分析水平荷载作用下群桩周围岩土体位移和应力云图发现群桩效应最显著位置位于桩群中心位置,表现为中心位置岩土体水平位移最大,且抵抗水平荷载能力最差。
(3)通过分析桩距与桩径比、弹性模量及泊松比对群桩效率的影响发现,桩距与桩径比、弹性模量对群桩效应影响显著,表现为正相关,而泊松比对群桩效应影响可忽略不计,验证了群桩效率公式中影响因素设置的合理性。
(4)通过对比不同排列形式群桩的公式法和数值法群桩效率计算结果,证明了本文提出的公式法可以很好地反应桩距与桩径比和弹性模量对群桩效率的影响。

