拉式中央斜置螺旋弹簧离合器功能分析及负荷特性计算

张勇

摘要：拉式中央斜置螺旋弹簧离合器因其压紧载荷稳定，分离力小的性能特点，同时具有补偿调节和分离制动功能，在美国重型卡车上得以广泛使用。本文结合开发实例，对该结构离合器零部件展开了质量功能分析，并采用计算赋值描点的计算方法推导了其丝毫不逊色于膜片弹簧的非线性负荷特性曲线。

关键词：中央斜置;螺旋弹簧;离合器;补偿调节;功能分析;非线性负荷特性

中图分类号：U463.211                                   文獻标识码：A                                文章编号：1674-957X（2021）08-0064-03

1  简述

离合器作为汽车重要的传动零部件之一，传统结构已使用了一百余年。随着人们对汽车可靠性、舒适性等要求的不断提高，也对传统离合器提出了更高挑战，一些高性能汽车零部件应运而生，如AT、AMT、DCT、CVT、双质量飞轮、自动补偿离合器……。上个世纪八十年代，传统的螺旋弹簧压盖总成被性能优良的膜片弹簧压盖总成逐步取代，继而不断发展成推式、拉式、推拉式、双片拉式等多品种产品。可实现传递功率从150马力到600马力。然而，在美国重型卡车市场很大部分使用的是“拉式中央斜置螺旋弹簧离合器”，有单片、双片，并在上百种发动机上使用，其非线性负荷特性丝毫不逊色于膜片弹簧离合器。

2  功能分析

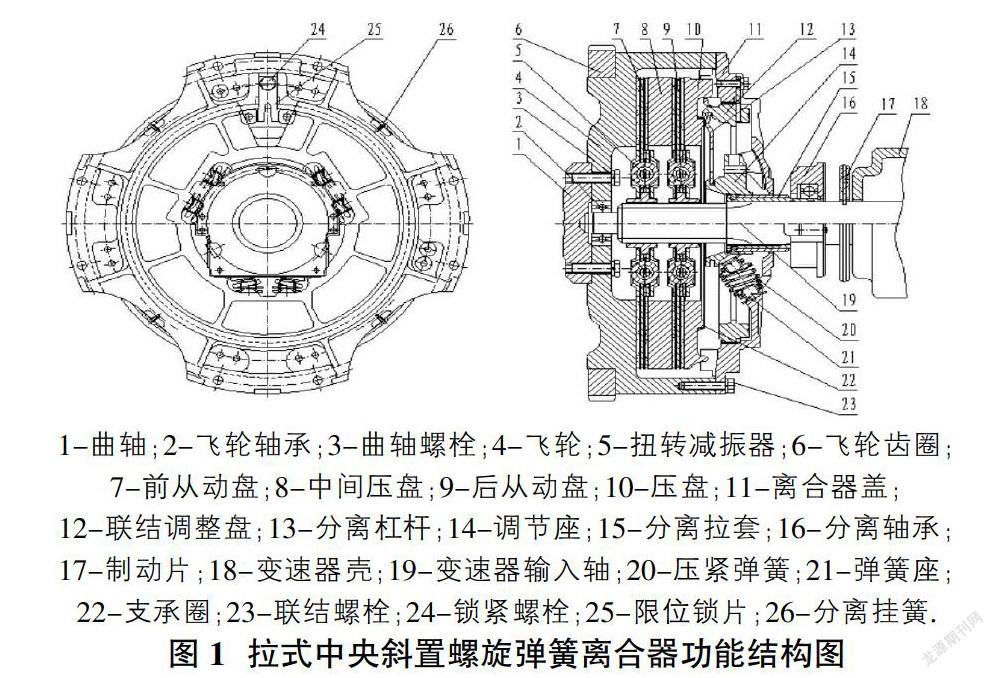
拉式中央斜置螺旋弹簧离合器大多采用3对斜置的螺旋弹簧产生工作压紧载荷，其结构如图1。（本文结合￠350离合器实例分析及计算）

如图1所示，压紧弹簧（件20）安装在离合器盖（件11）与弹簧调节座（件14）之间，调节座（件14）固定在分离拉套（件15）上，弹簧（件20）产生的轴向分力经调节座（件14）作用在分离杠杆（件13）小端，分离杠杆（件13）的杠杆支点在联结调整盘（件12）联接处，可自由转动，而调整盘（件12）则通过螺纹联接固定在离合器盖（件11）上，分离杠杆（件13）支点前方折弯成型形成另一支点作用在支承圈（件22）和压盘（件10）上，压盘（件10）和离合器盖（件11）之间采用凸耳传递扭矩。

当离合器接合时，压盘（件10）工作载荷由弹簧（件20）沿变速器输入轴轴线方向上的分力经分离杠杆（件13）放大杠杆比（i=5）产生。当离合器分离时，分离轴承（件16）通过分离拉套（件15）将弹簧调节座（件14）后拉（拉向变速器方向），分离杠杆（件13）指端同时后移，压盘（件10）不再承受轴向压力，在分离挂簧（件26）的作用下脱离从动盘摩擦面片，从而彻底有效分离，切断动力传递。

这种放大杠杆比的结构设计，有效的降低了分离力，但也带来了分离指端高度不稳定、变化大的缺点，若从动盘磨损3mm，分离指端要前移15mm，分离时，压盘抬升2mm，分离指端后拉10mm，如果是双片离合器主压盘抬升量3.5mm，则分离指端要后拉17.5mm，如此大的分离行程和磨损预留空间给离合器操纵系统的设计带来困难。因此该产品结构设计中，采用联结调整盘（件12）调整分离杠杆支点，来弥补因摩擦面片磨损而引起的分离指端前移量。摩擦面片磨损一定程度时进行调整，调整时，松开锁紧螺栓（件24），取下限位锁片（件25），向前旋转调整盘螺纹，旋转一周杠杆支点前移2mm（螺距为2的情况下），分离指端相应后移10mm，调整确认后，再用锁紧螺栓（件24）将限位锁片（件25）锁紧，由此保证分离指高度的稳定或不变。

分离制动功能主要靠分离轴承（件16）和制动片（件17）完成。离合器分离时，当分离轴承（件16）后移到一定位置，轴承后盖板与固定在变速器输入轴上的制动片（件17）相接触，在摩擦力作用下，使变速器输入轴及从动盘总成转速降低。因此，在保证分离行程满足需要的前提下，调整离合器踏板及分离拨叉的行程量可以控制分离制动的大小、有无，进而有效降低换挡冲击，更好的保护相关传动零部件。

3  工作特性分析

由压紧弹簧产生的轴向分力经杠杆比放大后作用在压盘上的工作载荷大小，不仅与弹簧沿其轴线的压缩变形量有关，还和弹簧轴线与变速器输入轴轴线的夹角大小有关。

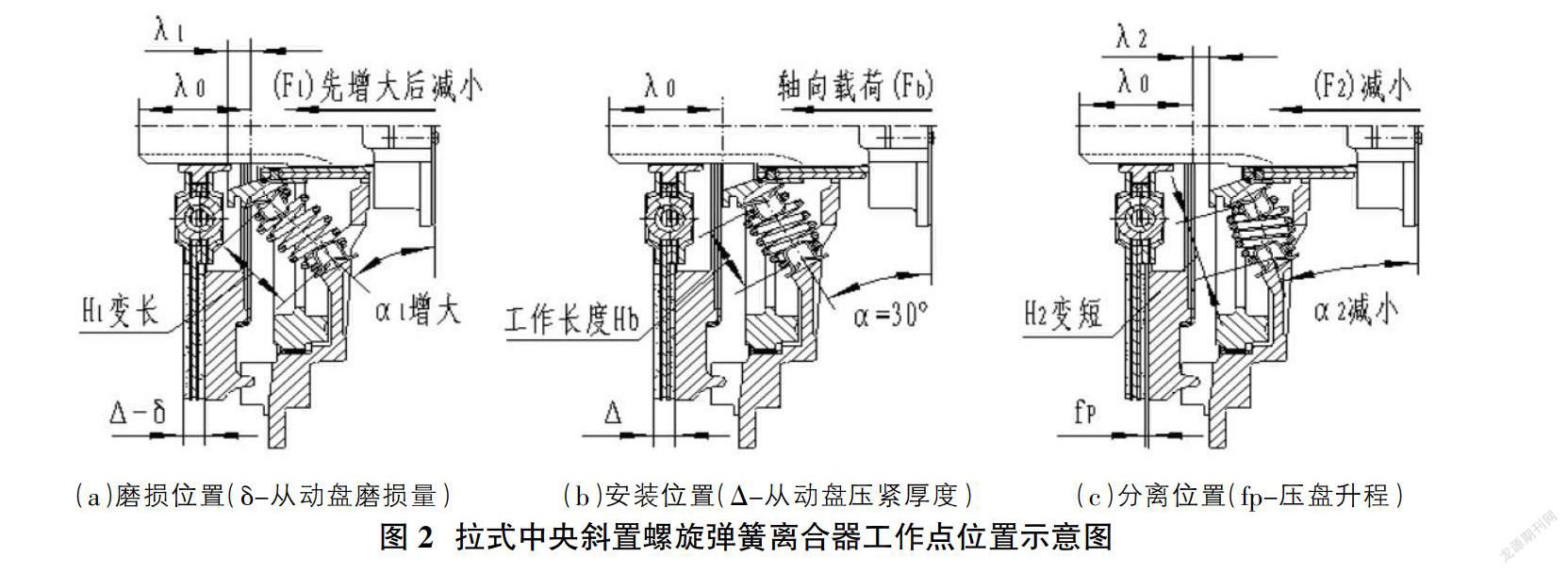
如后面的计算，离合器在初始安装位置图2（b），一个弹簧的工作载荷是742.5N，沿输入轴轴向分力为371.25N，6个弹簧的轴向载荷即2227.5N，经分离杠杆放大后，总的工作压紧力为11137.5N，而此时小端分离力仅为2227.5N。

当摩擦面片磨损后图2（a），弹簧工作长度虽变长，但其轴线与输入轴垂直面夹角增大，轴向分力随此的变化是先增大后减小，保证了摩擦面片磨损时工作载荷稳定。

当离合器分离时图2（c），弹簧工作长度虽变短，工作载荷增大，但其轴线与输入轴垂直面夹角减小，使得轴向分力反而减小，保证了分离点分离力较小。

4  负荷特性计算

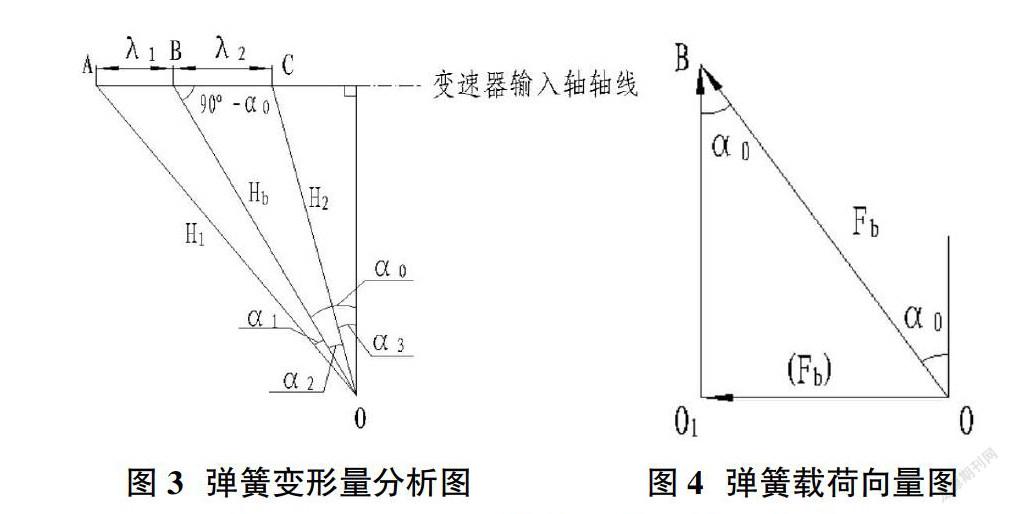
由前面的结构功能和工作特性分析可清楚了解，离合器工作压紧载荷是有斜置的螺旋弹簧产生。压紧弹簧在工作时的受力分析见图3、图4。

图3、图4中：λ1-面片磨损后小端前移位移量;Fb-安装状态弹簧工作载荷;λ2-分离行程;Hb-安装状态弹簧工作长度;（Fb）-弹簧载荷轴向分力;H1、H2、λ1、λ2变化时弹簧工作长度;α0-安装状态弹簧轴线与输入轴垂直面夹角。

其中，λ1、λ2、H1、H2为变量，Hf、Hb、α0为给定已知量（Hf是弹簧自由长度）。

ΔABO中：AO2=AB2+BO2-2×AB×BO×cos（900+α0）

即：H12=λ12+Hb2+2×λ1×Hb×sinα0   （1）

已知Hb、α0，当λ1赋值时，得到对应H1和α1值;

ΔBCO中：CO2=BO2+BC2-2×BO×BC×cos（900-α0）

即：H22=Hb2+λ22-2×Hb×λ2×sinα0    （3）

同樣当λ2赋值时，得到对应H2和α2值;

压紧弹簧在安装长度Hb时的工作载荷Fb=g（Hf-Hb）

因此，变速器输入轴轴向分载荷（Fb）=Fb×sinα0=g（Hf-Hb）sinα0

同理得到：（F1）=F1×sin（α1+α0）=g（Hf-H1）sin（α1+α0）

（5）

（F2）=F2×sin（α0-α2）=g（Hf-H2）sin（α0-α2）（6）

H1与λ1的关系是较复杂的非线性关系，对应于H1的F1与λ1的也同样存在较复杂的非线性关系，再转算成（F1），这样的行程与力值关系难以用一条函数曲线来表达，应是抛物线和正弦线的叠加。在此，可用赋值法研究位移与载荷变量之间的方向性变化。

给定：α0=300、Hf=75、Hb=42、g=22.5N/mm，摩擦面片磨损后，Hb变成H1，且H1>Hb

当λ1=1时，代入（1）计算：H12=1807.1即H1=42.51。

代入（2）计算：α1=1.170代入（5）计算：（F1）=378.35N;

同理，可以计算出λ1不同赋值时对应的F1、（F1）、α1值，见表1，结合图2（a）清楚看出，随着摩擦面片磨损，λ1增大，H1变长，F1降低，但α1在加大，压盘正向载荷（F1）相应在变化，α1在小角度范围内变化，λ1增大，H1增加不明显，而（F1）增大明显，而α1在大角度范围内变化，λ1增大，H1增加变得明显，F1下降明显，而（F1）增大不再明显，后又逐渐减小。显然，先增加后减少，必然有一个交叉峰值点。本例，峰值点发生在α1=8.60左右（即λ1=8mm时）。

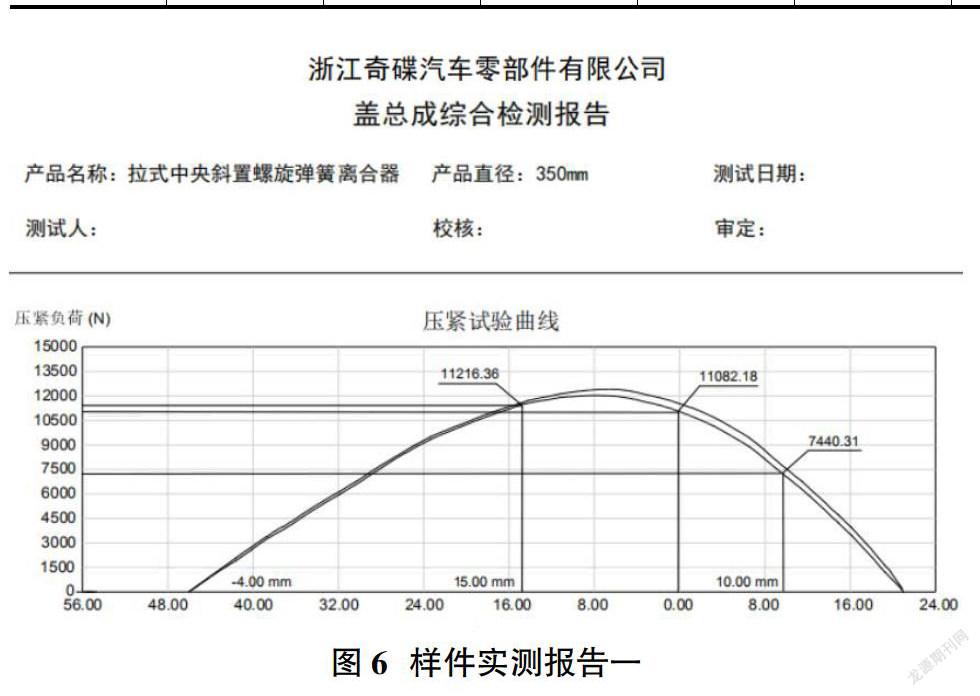
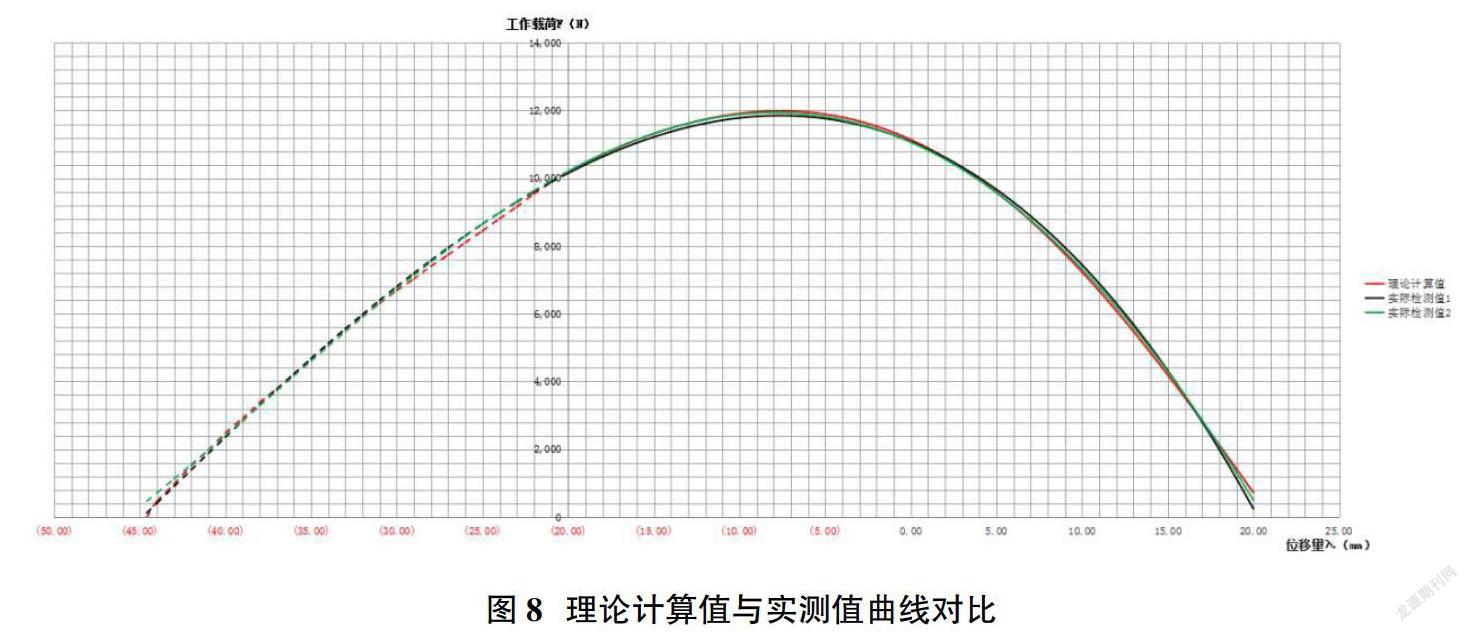
又当分离轴承后拉分离时，Hb变成H2，且H2

H22=1722.3 即H2= 41.51  代入（4）计算：α2=1.190

代入（6）计算：（F2）=363.07N

同理，可以计算出λ2不同赋值时对应的F2、（F2）、α2值，结合图2（c）可以看出，随着分离行程λ2增加，H2变短，F2变大，但α2在减小，而（F2）随之减小。由初始安装工作点（即弹簧长度Hb=42mm时）开始，将所计算的数据描点合并，便得到了随小端位移量λ变化对应的大端工作载荷变化的负荷特性曲线，如图5。

由曲线我们可以清楚看出，当摩擦片磨损3mm后（即分离轴承前移，λ1=15mm时），工作点载荷几乎不变;而离合器彻底分离时（即分离轴承后拉，λ2=10mm时），分离力却下降了35%，这充分体现出其具备良好的非线性负荷性能曲线。

5  产品实测数据比对

根据产品实际开发情况，对实际生产制造样件在专用的离合器综合性能检测设备上对负荷特性进行检测，图6图7为两台样件实测检测数据记录。

同时将理论计算值及赋值获得的曲线和两台样件实测数据和曲线进行吻合性比对，见图8。各位移点对应载荷最大误差在2%以内，充分表明了赋值计算和生产件实测值具备良好的吻合度。

6  产品结构优缺点分析

优点：压力大、稳定，分离力小，可调节补偿从动盘摩擦面片磨损，拉式结构带分离制动装置，便于换档。

缺点：结构较复杂，工艺成本较高，但随产量大，工艺成本摊销也就不足为虑了，运动摩擦副较多，摩擦力大，尤其是在“连结调整盘”与分离杆连结处，正压力大，所以摩擦力大难以克服。

参考文献：

[1]林世裕.膜片弹簧与碟形弹簧离合器的设计与制造[M].南京：东南大学出版社，1995，12.

[2]徐石安，江发潮.汽车离合器[M].北京：清华大学出版社，2005，8.

[3]严正峰，张铁山.汽车离合器设计与制造[M].北京：机械工业出版社，2018.