动力总成悬置系统优化设计及系统稳健性分析
李聪 张帆 杨玉玲 覃臻 覃丽霜 蒋斌文



摘要:建立动力总成6自由度模型,以能量解耦为优化目标,系统频率分布及悬置各向刚度比值为约束,悬置各向刚度为变量,采用遗传算法对系统进行优化设计。运用Monte Carlo方法对结果可靠性进行验证。最后通过实车测试验证悬置系统的隔振性能。
Abstract: A 6 DOF model for powertrain mount system is established, Taking the energe decoupling method as the objective, system frequencies and stiffness ratio of each mount as constrains, stiffness of each mount as variables, the optimization of mounting system is conducted using genetic algorithm. The result reliability is checked using Monte Carlo method. Finally the performance of mounting system is verified by vehicle testing.
關键词:动力总成悬置系统;能量解耦;遗传算法;优化设计;可靠性
Key words: powertrain mount system;energe decoupling;genetic algorithm;optimization design;reliability
中图分类号:U464.1 文献标识码:A 文章编号:1674-957X(2021)08-0014-04
0 引言
随着人们生活水平的提高及汽车技术和汽车工业的不断发展,人们对汽车的乘坐舒适性要求越来越高,对汽车的振动、噪声越来越关注。发动机是汽车最主要的振源,其振动通过悬置系统传递到车身上,最终影响整车振动、噪声水平及舒适性。动力总成悬置系统除支撑动力总成外,其主要功能为隔离发动机振动,减少振动向车身的传递,因此悬置系统匹配设计对整车振动、噪声及舒适性至关重要。
悬置系统隔振性能的优劣与悬置安装位置、悬置各向刚度因素相关[1],在追求解耦率最大的同时需满足动力总成悬置系统各阶频率合理分布及悬置结构的可制造性。在设计变量、约束条件、优化目标都较多的情况下,要做到设计最优需要一套有效的优化方法。根据目前橡胶的生产工艺及控制水平,实测悬置刚度与设计值的误差通常在±10%以内,较大的刚度误差可能引起系统的不稳定,因此需对系统稳健性进行分析,以保证在制造误差内悬置系统都有较好的表现。本文采用MATLAB及ISIGHT软件对某车型悬置系统进行优化设计,并采用Monte Carlo方法对结果的可靠性进行验证,最后通过实车测试验证了悬置系统的隔振性能。
1 动力总成悬置系统六自由度模型
动力总成通过悬置系统固定到车身上,理论上动力总成及车身均具有一定刚度,橡胶悬置在三维空间上均有平动刚度及扭转刚度,橡胶同时具有阻尼,整个动力总成悬置系统为一个复杂的弹性阻尼系统。基于以下原因并做以下几点简化:
①动力总成及车身刚度远大于悬置刚度,可将动力总成及车身视为刚体;
②把橡胶简化为3个正交方向的弹簧;
③考虑到各悬置的相对距离较近,且平动刚度较大,可忽略橡胶扭转刚度;
④由于橡胶阻尼较小,在小幅振动的情况下可忽略橡胶阻尼。
定义坐标系G0-xyz,其中G0为动力总成质心,x轴沿曲轴方向指向发动机自由端,z轴沿气缸轴线指向缸盖方向,y轴由右手定则确定。橡胶悬置弹性主轴坐标u、v、w分别为悬置的3条弹性主轴。
动力总成悬置系统有x、y、z3个方向的平动和绕x、y、z3个方向的转动,多自由度振动系统的振动微分方程式为[1]:
其中:
M——系统质量矩阵;
C——系统阻尼矩阵;
K——系统刚度矩阵;
F(t)——系统所受激励向量。
固有频率和模态方程为[2]:
由式(2)可得系统的主振型方程:
2 动力总成悬置系统的优化设计
动力总成6自由度运动通常相互耦合,耦合振动使得系统振动加剧,因此解耦设计成为目前动力总成设计的常用方法之一。本文以能量解耦[3]为目标对某车型悬置系统参数进行优化。
2.1 优化目标函数及目标
当动力总成悬置系统以第i阶固有频率和振型振动时,第k个广义自由度上能量占总能量的百分比为:
其中:mkl——M的第k行l列元素;
i——系统的第i阶主阵型。
动力总成6自由度中沿z轴的平动(Bounce)及绕x轴的转动(动力总成横置为Pitch,动力总成纵置为Roll)为最主要的2个自由度,通常要求解耦率大于90%。其余方向通常要求大于80%。
2.2 设计变量
2.2.1 悬置安装位置{x1,y1,z1,x2,y2,z2,x3,y3,z3}
安装位置包括各悬置的x、y、z坐标,本文实例为三点悬置,即包含左、右、后三个悬置的x、y、z坐标,共9个变量。
2.2.2 悬置安装倾角{?兹x1,?兹y1,?兹z1,?兹x2,?兹y2,?兹z2,?兹x3,?兹y3,?兹z3}
各悬置弹性主轴与整车坐标系的夹角,本文实例为三个悬置弹性主轴与整车坐标系x、y、z坐标的夹角,共9个变量。
2.2.3 悬置刚度{Kx1,Ky1,Kz1,Kx2,Ky2,Kz2,Kx3,Ky3,Kz3}
各悬置三个弹性主轴的刚度值,本文实例为左右后三个悬置u、v、w三个弹性主轴的刚度值,共9个设计变量。
2.3 约束条件
在悬置设计时悬置的布置位置和倾角往往受到诸多限制,如三点带防扭拉杆悬置往往要求左右悬置布置在扭矩轴附近,另外车身及动力总成安装点以及周围其他零件布置的需要都将悬置的安装位置及倾角限制在一定的范围内。
6阶固有频率首先应小于激励力频率的1/,只有小于激励力频率的1/才能起到隔振效果[4],同时各阶频率应与整车其他相关系统可能造成共振的频率分隔开来,如6阶固有频率应避免与前悬跳动频率的耦合,应避免人体敏感频率5~7Hz的耦合等。
橡胶悬置受橡膠材料性能及结构限制,每种结构悬置的各向刚度比值必须限制在一定范围内才能制造出来,否则会造成优化结果很好而实际无法制造出满足各向刚度要求的悬置。
橡胶悬置应具备足够的静刚度,避免因悬置过软造成橡胶的剪切破坏,降低悬置的使用寿命,如通常悬置的静载位移控制在6mm以内。
2.4 优化设计
动力总成悬置系统优化涉及优化变量多、约束条件多,且同时有多个优化目标,该优化问题较为复杂,存在较多的局部最优解。采用传统优化方法很难得出结果,或者难以得到较优的解。遗传算法能够有效防止优化结果限于局部最优解,得到全局最优解的概率大大增强。
遗传算法是一种类似于生物进化的优化方法。它通过选择、交叉、变异的循环寻求最优值。遗传算法中采用适应度来衡量群体中各个个体在优化计算中有可能达到或接近于找到最优解的优良程度[5]。
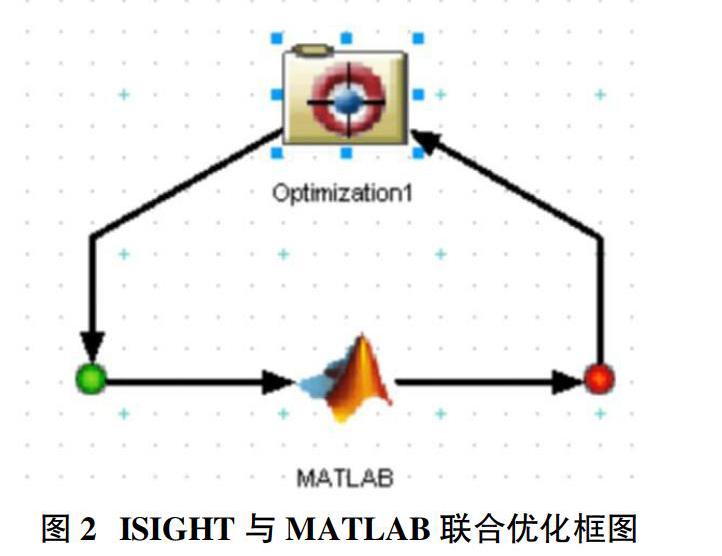
本文采用MATLAB编程对悬置系统固有频率、解耦率进行计算,然后应用ISIGHT平台调用MATLAB所编写的程序进行优化设计。MATLAB编程语言便于对质量矩阵和刚度矩阵的操作,特别是对于矩阵特征值和特征向量的计算尤其方便。ISIGH是EngineousSoftware公司开发的基于WindowsNT和Unix平台的过程集成、优化设计和稳健性设计的软件,它可以将数字技术、推理技术和设计探索技术有效融合,并把大量的需要人工完成的工作由软件实现自动化处理,好似一个软件机器人在代替工程设计人员进行重复性的、易出错的数字处理和设计处理工作。iSIGHT软件可以集成仿真代码并提供设计智能支持,从而对多个设计可选方案进行评估、研究,大大缩短了产品的设计周期。采用ISIGHT与MATLAB联合优化充分结合了两个软件的优势使得优化设计计算程序更加便利、高效,程序框图如图2所示。
本文以某车型为例,其输入质量参数如表1所示,其中质量单位为kg,惯量参数单位为kg.m2。
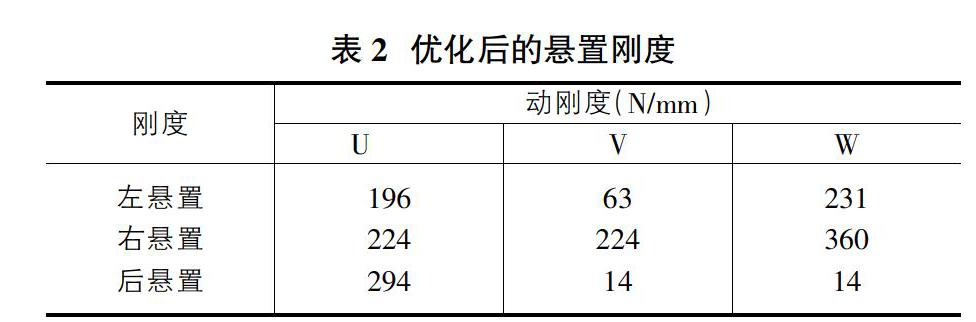
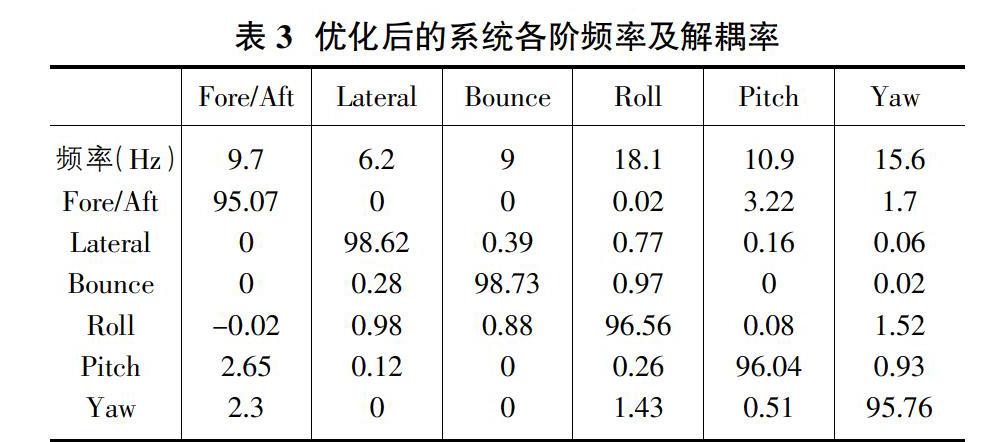
由表1参数,采用MATLAB及ISIGHT对悬置系统进行优化,由于悬置类型及受整车布置的限制,本实例仅优化悬置刚度,悬置安装位置及安装角度不做优化。联合优化后的悬置刚度如表2所示,系统各阶频率及解耦率如表3所示。
该车型为三点悬置,其中左悬置为变速器侧悬置,该悬置为衬套式悬置,其压剪比为3.7满足压剪比3~8的范围;右悬置为发动机侧悬置,其结构为圆筒形,U、V方向刚度相同,便于制造;后悬置为防扭拉杆,V、W方向刚度为等效刚度[6]。因此左、右、后三个悬置刚度均满足制造要求。
在表1刚度的基础上计算左、右悬置的静载位移分别为5.4mm和5.2mm。悬置静载位移小于6mm,悬置耐久性可满足要求。
由表3可知2个主要方向Bounce(上下平动)及Pitch(绕曲轴转动)的解耦率分别达到了98.73%和96.04%,解耦效果较好。同时其他非主要方向的解耦率也都超过了95%,总体解耦效果较好。
发动机怠速转速为750R/min,其对应二阶频率为25Hz,由表2可知除Roll方向频率外其余频率均小于激励力频率的1/(17.7Hz),考虑到Roll方向为非主要方向,结合整车振动实测没有出现共振的情况下,频率略高可以接受,Bounce方向的固有频率避开了人体敏感频率5~7Hz和前悬跳动频率12~14Hz。
3 动力总成悬置系统的可靠性验证
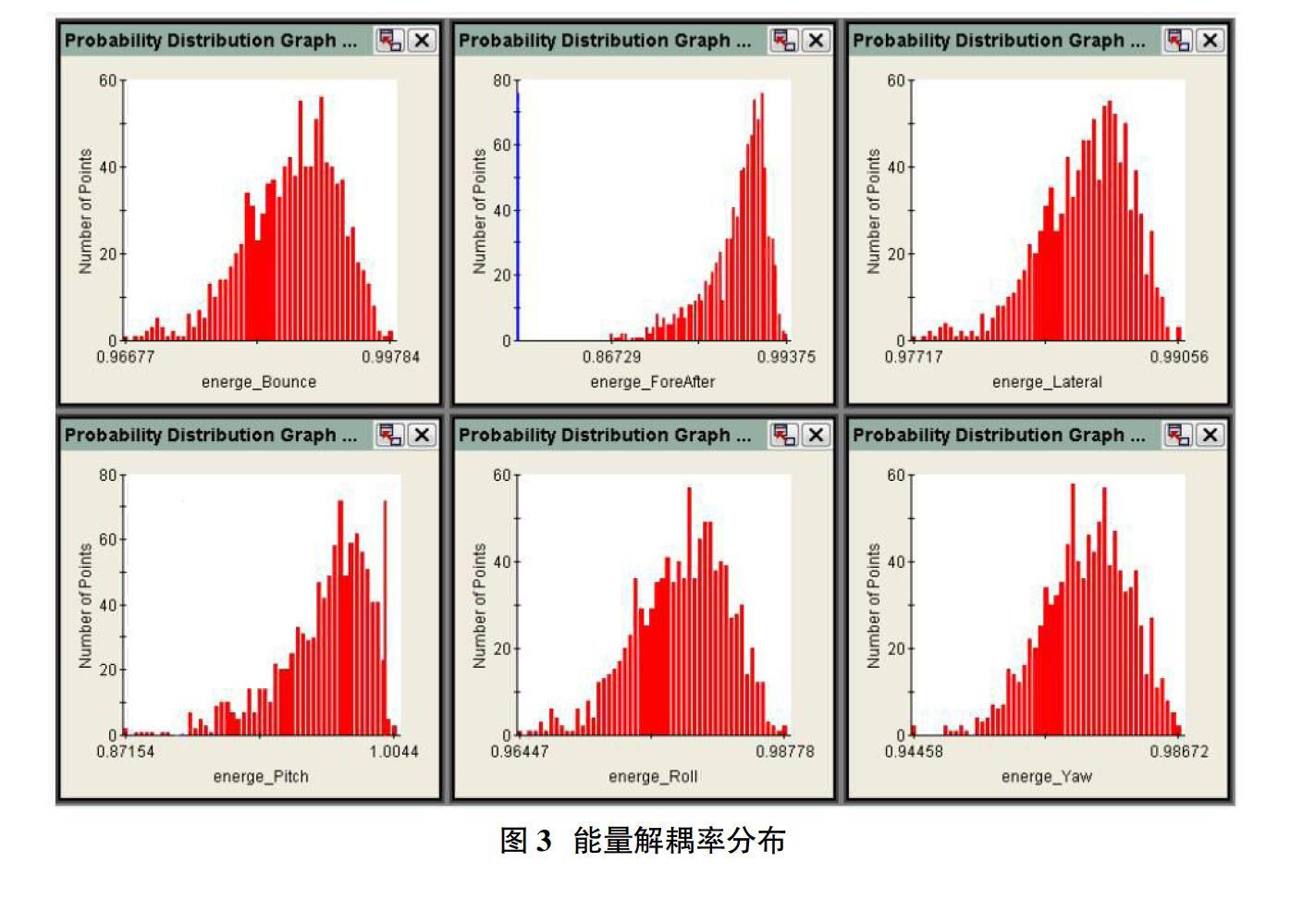
动力总成悬置系统刚度经优化后,系统解耦效果较好,但该解耦结果均是在理想刚度值的前提下得到,而实际悬置生产过程中由于制造误差及橡胶工艺的特殊性,实测悬置刚度与设计值的误差通常在±10%以内,在这较大的误差范围内,系统解耦率是否能达到要求,系统可靠性能否得到保证都需要进一步验证。本文采用Monte Carlo法对动力总成悬置系统的可靠性进行验证。Monte Carlo法又称为统计试验法,通过产生服从一定分布的随机变量,计算响应值的分布情况,以确定变量对响应值的影响。设置各个刚度变量的数目为1000,各悬置的刚度值在±10%的范围内变化,且满足正态分布。经计算得到6个方向的能量解耦率如图3所示。
由图3可知Bounce(上下平动)方向解耦率均大于96.7%,Pitch(绕曲轴转动)方向的解耦率主要分布在90%以上,其余各方向解耦率也都大于85%,由此可知系统稳定性较好。
4 测试验证
以解耦率为优化目标设计悬置系统从理论上保证了悬置系统的隔振性能,本文采用实车测试进一步证明悬置系统的隔振性能。隔振率为评价悬置系统隔振性能的重要指标,本文测试了某车型在怠速及三档全油门工况下各悬置的隔振率如图4和图5所示。由图4可知怠速工况下,左、右、后三个悬置的隔振率均达到20dB以上,即动力总成振动通过悬置后振动量衰减90%以上,悬置系统怠速隔振性能良好。由图5可知三档全油门工况下左悬置隔振率接近20dB,右悬置及后悬置隔振率大于20dB,因此在三档全油门工况下悬置隔振性能较好。
5 结论
本文采用ISIGHT及MATLAB,基于遗传算法,以解耦率为目标对动力总成悬置系统进行设计,并采用Monte Carlo法验证了悬置系统在考虑制造误差情况下的可靠性,最后对设计生产出的悬置系统进行实车测试,测试结果表明悬置系统隔振性能良好,优化设计及验证方法可靠。
参考文献:
[1]徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程,1955,17(4):198-204.
[2]阎红玉,徐石安.发动机—悬置系统的能量法解耦及优化设计[J].汽车工程,1993,15(6):321-328.
[3]赵彤航.CA1261汽车发动机悬置系统隔振的研究[D].吉林大学硕士学位论文,2002.
[4]庞剑,谌刚,何华.汽车噪声与振动—理论与应用[M].北京:北京理工大学出版社,2006.
[5]周明,等.遗传算法原理及应用[M].北京:国防工业出版社, 1999.
[6]上官文斌,徐驰,黄振磊,李岐,李涛.汽车动力总成悬置系统位移控制设计计算方法[J].汽车工程,2006,28(8):738-742.

