随机通胀下基于终止风险的DB养老金计划的保费估值
何学强, 王传玉,余 鑫
(安徽工程大学 数理与金融学院,安徽 芜湖 241000)
在养老金计划的设计中,根据缴费和支付方式的不同,可以分为确定给付(Defined Benefit,DB)型和确定缴费(Defined Contribution,DC)型计划。DB养老金计划中养老基金是养老金支付的主要来源,养老金计划发起人在需要时有道德义务向养老金计划提供支持。如果养老金计划出现赤字问题和发起人公司破产,那么DB养老金计划会出现养老基金提前终止和发起人资产遇险终止两种风险。一旦出现这两种风险,员工退休时的收益就得不到保障。因此,DB养老金计划通过引入PBGC为养老金计划提供担保,使养老金计划受益人能够从PBGC获得足够的养老金。作为回报,养老金计划发起人需要支付一笔保费给PBGC以确保利益。研究的目的是确定PBGC应该为其保险收取的价格,以保持财务稳定,从而实现自筹资金。
关于PBGC保费计算的一系列工作中,最早的工作可以追溯到Sharpe,Sharpe假定PBGC是解决养老基金赤字的第一条途径。Marcus将PBGC的负债建模为远期合约,这使得PBGC能够从终止的计划中获得盈余,然而这是不太现实的,因为法律不允许PBGC的责任是消极的。Lewis通过为公司的非养老金资产建立独立的随机过程来计算养老金保险的理论保费、非养老金债务、养老基金和养老金负债,并将PBGC的负债建模为看跌期权合约。Bodie和Brown的工作表明,从PBGC的角度来看,统一保费是错误的,而定价不当的养老保险对计划发起人是有害的。而Stewart提供了背后的经济理由和相关后果,经济的理由是,对有风险的公司来说,收取固定的保费会导致股票的市场价值增加,从而为赞助商提供更多风险和资金的激励。另一个研究的方向是设计PBGC的终止或监管规则,以及一般的养老金担保制度。Cheng根据关键资金比率提出了一项养老金保障保险的终止规则,这是通过解决优化问题而实现的。此外,养老金监管至关重要。Chen的研究中说明,养老金福利可以通过各种方式得到保障,与养老基金提供的保护相比,担保人的援助只提供了全额养老金支付的部分保障,将偿付能力要求与养老保障基金和担保人支持相比较。偿付能力要求提供了内部缓冲,而养老保障基金和担保人援助作为外部担保机制。Chen进一步了解养老基金的最佳监管规则,并发现监管机构需要充分考虑安全机制和风险措施。
Kalra首先考虑了养老基金的提前终止,并研究了这类非自愿终止的保费评估问题。然后Chen在完备市场下讨论了养老基金的提前终止,假设PBGC作为二级保险担保发挥作用。考虑到PBGC仅涵盖养老基金的剩余赤字,并建立养老基金资产和发起人资产模型,该模型解释了养老基金和发起人公司的资产的联合动态,有效地确定PBGC提供的基于风险的养老金保险的保费,还用积分的方法得到了这种基于提前终止风险的保费的封闭定价公式。接着Chen在Chen的基础上建立了养老金担保公司(PBGC)提供的基于风险的保险费计算模型。并且考虑到养老基金和计划发起人的投资政策,还考虑到发起人资金不足引发的遇险终止,实证地说明了对100家最大的美国DB赞助公司的理论定价公式。还观察到,在基于风险的保费计算中,资金比率和杠杆是主要的风险因素。Qian首次在同时考虑提前终止和遇险终止的条件下研究PBGC为DB养老金计划担保所收取的保费估值问题。
文献[1-13]逐步完善了PBGC为养老金计划担保的保费计算问题的研究,从最开始不考虑养老金计划终止的情况,到后来单独考虑提前终止或遇险终止,再到后来同时考虑两种终止情况时的保费计算。虽然这些研究为养老金计划机制的完善提供了理论依据,但是之前的研究都是在理想的条件下进行的,例如无通货膨胀。这就会导致研究结果与现实会有较大的差异,即这些研究结果的应用伴随着一定的风险。而在金融市场中,通货膨胀是实际存在的,因此,研究在前人的基础上引入随机通胀因素,这样得出的结果会与现实更接近。
近几年通货膨胀对金融市场的影响越发显著,因此,在研究DB养老金计划基于风险的保费时必须考虑随机通胀因素。那么如何引入随机通胀就是首先要考虑的问题,其次就是保费计算模型的建立,最后的问题就是数值模拟。研究在Qian的基础上引用了王照中的随机通胀模型,假设随机通胀也是一个随机过程,其收益水平满足一个微分方程,养老基金资产和发起人资产在随机通胀下的真实价值就等于无通胀时的价值除以随机通胀的收益水平。然后给出提前终止和遇险终止触发的条件,并对提前终止时间和遇险终止时间进行分析,得出PBGC在提前终止、遇险终止以及没有提前终止和遇险终止这三种情况下对DB养老金计划提供的资金援助。建立两个终止时间的联合终止概率密度表达式,通过对两种终止时间的讨论,得出提前终止、遇险终止以及没有提前终止和遇险终止这三种情况下PBGC对DB养老金计划提供的资金的均值,然后给出计划发起人需要交给PBGC的保费的定价公式。最后,对结果进行数值模拟,分析随机通胀对PBGC收取的保费的影响并比较了研究模型与Qian的模型。
1 模型构建与假设
研究单一雇主的DB养老金计划的养老金保险。假设养老金计划在0时向α
岁的一名代表受益人发放,该福利在T
时作为一笔一次性付款支付给R
岁的该受益人。那么支付时间T=R
-α
。从Qian1的研究出发,可以假设雇主有义务支付给受益人的福利为:
(
1)
式中,
p
是α
岁的代表受益人至少活了j
年的概率;r>
0是无风险利率;F
是规定的年度福利,具体取决于雇员服务年数、退休年龄、福利乘数和收入历史。虽然时变利率或随机利率可能更为现实,并对养老金支付产生影响,假设认为利率是固定的。主要研究目标是在随机通货膨胀下养老金发起人和养老基金对PBGC保费支付的影响。假设所有过程和随机变量都定义在带流概率空间(Ω,F,{F
}
0≤≤,P)
上,且满足一般条件,其中P
表示真实概率测度。而完备的金融市场是由无风险金融资产(
例如银行存款)
和有风险金融资产(
例如股票)
组成。两种资产的定价过程为:dB
=rB
dt,
(
2)
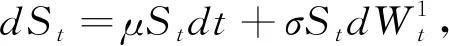
(
3)



(
4)
假设养老基金表现良好,那么所有福利都将由养老基金自己支付。如果养老基金资金不足,那么发起人的资产将是支付福利的潜在资源。发起人资产a
满足下面的微分方程:
(
5)
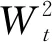
Q
满足下面的微分方程:

(
6)

t
时刻的养老基金总资产的真实资产为:

发起人公司资产的真实资产为:

则

(
7)

(
8)
在风险中性测度下,养老基金和发起人资产的表达式为:
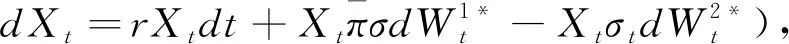
(
9)

(
10)
由伊藤公式解得:


2 计划发起人和PBGC对养老金计划提供的资金
对于标准终止,无论是计划发起人还是PBGC都没有义务对养老金计划提供资金援助。研究的重点是考虑养老金计划提前终止和遇险终止。
为了描述每种类型的终止,首先介绍一些关键的符号。对于养老基金的提前终止,定义了养老基金在t
时刻的临界值是ηB
e
--,其中B
e
--表示未来退休金支付在t
时刻的贴现值,η
是终止触发时的资产比例,也就是说,是一种乘数,允许养老基金在一段宽限期内恢复,以防它暂时表现不佳。因此,在养老基金资产第一次低于或越过临界值时,得到提前终止时间如下:
π
=inf{t|X
≤ηB
e
--},
(
11)
式中,如果η>
0,终止将永远不会发生,而η
≥1则意味着PBGC将作为完全资助的计划结束。假设η
∈(
0,
1)
,并且要求X
>ηB
e
-以确保最初的养老基金不会提前终止。遇险终止与计划发起人的资产有关,通常来说,计划发起人会发布公司债务。因此,假定发起人公司有责任在t
时偿还的债务为θA
e
,0<θ<
1是其初始杠杆率;v
是反映公司债务增长率的预定常数;A
是发起人资产的初始价值;θA
是计划发起人的初始债务水平。假定发起人公司优先偿还公司债务是合理的,使用停止时间τ
来描述计划发起人第一次未能支付债务和继续经营。这种终止的临界值被定义为ξA
e
。其中,ξ
是一个比计划发起人的杠杆比率θ
更高的参数。假设养老金发起人有道德上的义务来弥补所要求的养老金福利的一些赤字。此外,我们还规定了ξ<
1的技术条件,以确保发起人在0时刻不违约。因此,得到提前终止时间如下:τ
=inf{t|A
≤ξA
e
}
。(
12)
2.1 计划发起人对养老金计划提供的资金
在这一部分中,分析3种终止:标准、遇险和提前终止。对于标准终止,PBGC不提供任何资金。因此,只研究其他两种情况:τ
>τ
和τ
≤τ
。如果τ
>τ
,那么发起人公司破产,并将首先触发遇险终止。此外,将情况τ
≤τ
分成两个子情况:τ
≤T
和τ
>T
。(
1)
发起人资产在T
时刻之前低于临界值,即τ
≤T
。此时有:X
>ηB
e
--和A
=ξA
e
。①养老基金表现得很好,即X
>B
e
--。这意味着养老基金资产的价值大于所承诺的养老金福利付款的贴现值。这种情况下,计划发起人和PBGC都不要提供资金。②养老基金不足以支付所有贴现的养老金福利,即X
<B
e
--。虽然X
>ηB
e
--,但是仍然有可能使得X
<B
e
--。这时发起人公司提供的资金为:
S
(τ
)=(B
e
---X
)I
----×I
----+(ξ
-θ)A
e
I
---≥-×I
----,(
13)
式中,I
是示性函数;B
e
---X
指发起人公司的资产足以满足τ
时刻的养老金福利时,发起人公司能够承受的部分。因此,
这种情况下发起人公司将能够填补在此情况下养老基金的不足。另一种情况是,
当遇险终止发生时,
发起人公司在清偿到期债务后没有剩余多少资金,
此时提供的资金是(ξ
-θ)A
e
。(
2)
发起人资产在时刻T
之后低于临界值,即τ
>T
。这意味着X
>ηB
且A
>ξA
e
,且当τ
≥T
时,养老基金在到期日T
自然关闭。值得注意的是,如果X
≥B
,
那么无论是计划发起人还是PBGC都不需要介入并负责养老金的支付。因此,我们将专注于X
<B
继续进行分析。此时发起人公司提供的资金如下:S
(T)=(B
-X
)I
0--×I
I
+(A
-θA
e
)I
-≥-×I
I
,
(
14)
如果τ
≤τ
,提前终止将在遇险终止之前触发。我们也考虑两种情况:τ
≤T
和τ
>T
。(
1)
养老基金T
时刻前资金不足,即τ
≤T
。这意味着X
=ηB
e
--且A
>ξA
e
,这时养老基金面临提前终止,对于发起人资产有:①发起人公司有部分偿付能力,即
B
e
---X
>A
-θA
e
,
在这种情况下,PBGC提供了发起人公司无法承受的赤字比例。
②发起人公司表现足够好,即
B
e
---X
≤A
-θA
e
,
此时,受益人的养老金福利可以由发起人公司自己处理。
基于以上分析,可以从发起人公司获得资金如下:
S
(τ
)=(A
-θA
e
)I
1----×I
+(
1-η)B
e
--I
1---≤-×I
。(
15)
(2)养老基金低于临界值的时间不早于时刻T
,即τ
>T
。这时候有X
>ηB
且A
>ξA
e
。当τ
>T
时,养老基金在到期日T
自然关闭。只需要关注X
<B
的情况,因为X
≥B
意味着养老基金足以支付所承诺的养恤金。因此有S
(T)=(B
-X
)I
0--×I
I
+(A
-θA
e
)I
-≥-×I
I
。(
16)
发起人公司提供的全部资金为:
S
=[S
(τ
)I
≤+S
(T)I
]I
+[S
(τ
)I
≤+S
(T)I
]I
≥。2.2 PBGC对养老金计划提供的资金
与Chen和Chen相一致,PBGC是养老金支付过程中的第三条途径,它涵盖了养老基金和发起人公司无法支付的剩余赤字。因此,PBGC提供的资金如下:
如果τ
<τ
且τ
≤T,
即养老金计划发生遇险终止,则S
(τ
)=(B
e
---X
-(ξ
-θ)A
e
)
×I
---≥-×I
----。(
17)
如果τ
<τ
且τ
>T,
或者τ
≥τ
且τ
>T,
即养老基金在到期日T
自然关闭,
则S
(T)=(B
-X
-(A
-θA
e
))I
-≥-×I
I
。(
18)
如果τ
≥τ
且τ
≤T
,
即养老金计划发生提前终止,则S
(τ
)=((
1-η)B
e
---(A
-θA
e
))
×I
1----×I
。(
19)
结合以上4种情况,得出PBGC提供的资金为:
S
=[S
(τ
)I
≤+S
(T)I
]I
+[S
(τ
)I
≤+S
(T)I
]I
≥。(
20)
3 PBGC收取的保费
研究将推导PBGC在为养老金计划提供保险时应收取的基于风险的保费p
的计算公式。基于风险的保费定义为S
的贴现值的期望,如式(21)所示:
p=E
{[e
-S
(τ
)I
≤+e
-S
(T)I
]I
+[e
-S
(τ
)I
≤+e
-S
(T)I
]I
≥}
。(
21)


(
22)

(
23)
引理
1 设f
(z
,t)
,f
(z
,t)
,f(z
,z
,t)
分别表示Z
1,Z
2,(Z
1,Z
2)
的密度函数,
并且令
则
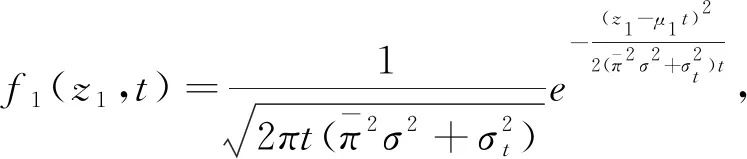

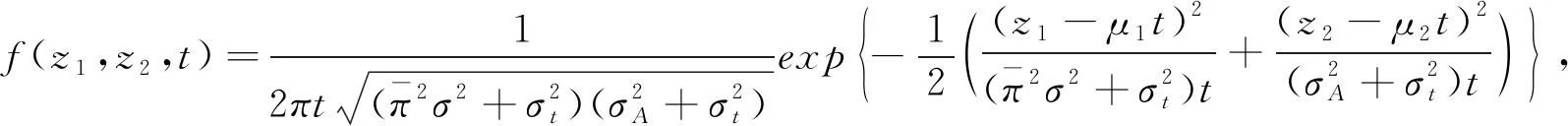
t
∈[
0,T]
。由于模型是同时分析不同类型的终止,所以无法使用τ
和τ
的边际密度函数来计算保费。将遇险终止和提前终止放在一个单一的框架内时,需要(τ
,τ
)
的联合密度作为计算的重要组成部分。g(t
,t
)
是通过时间(τ
,τ
)
的联合密度函数。如果τ
和τ
独立,则g(t
,t
)=g
(t
)g
(t
)
,而g
(t
)
和g
(t
)
表示τ
和τ
的边际密度函数。引理
2 设g
(t)
和g
(t)
分别表示τ
和τ
的密度函数,则



φ(
·)
表示标准正态随机变量的概率密度函数,t
∈[
0,T]
。证明
由Harrison
15可知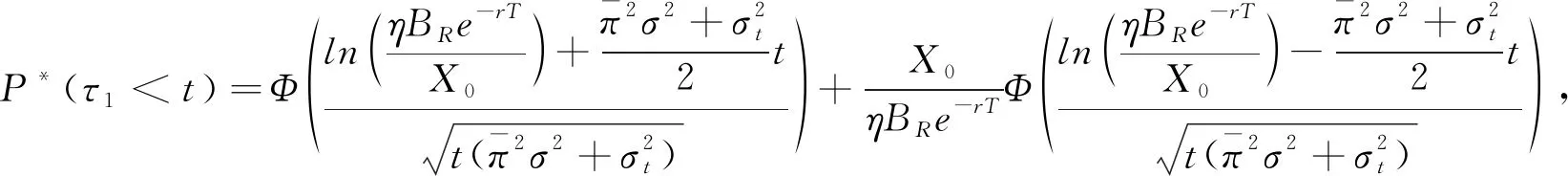
Φ(
·)
表示标准正态随机变量的累积分布函数。上式两边对t
求导,得到

同理可得
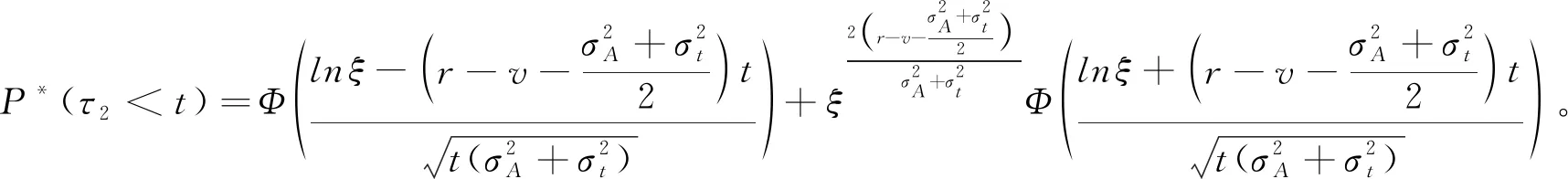

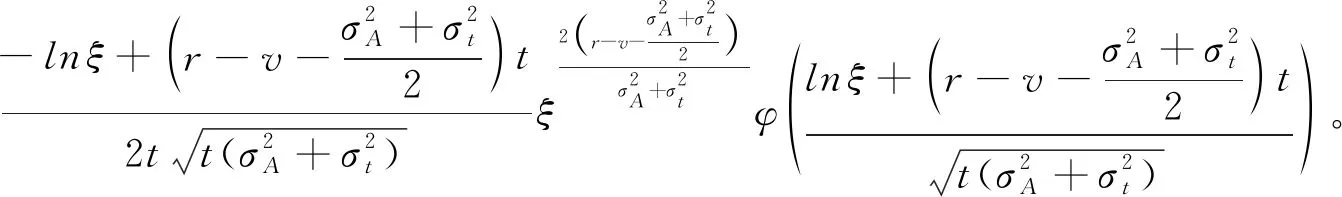
(
21)
分解成4个部分,即养老金计划遇险终止时,PBGC收取的保费为:p
=E
(e
-S
(τ
)I
≤I
),
养老金计划在计划到期日T
自然终止时,PBGC收取的保费为:p
=E
(e
-S
(T)I
I
),
养老金计划提前终止时,PBGC收取的保费为:
p
=E
(e
-S
(τ
)I
≤I
≥),
养老金计划在计划到期日T
自然终止时,PBGC收取的保费为:p
=E
(e
-S
(T)I
I
≥)
。在给出主要结果之前,先定义

和
D(t,x,y)=xB
e
--+yA
e
。定理
1 当无风险利率大于公司债务增长率时(r>v)
,PBGC保险的保费p
如下所示: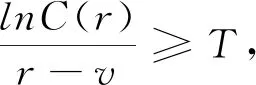


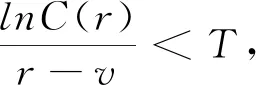
p=p
+p
+p
+p
=




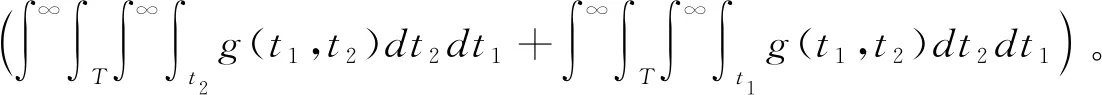
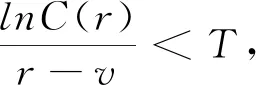


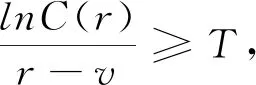
证明
根据式(
17)
可以得出p
=E
[e
-S
(τ
)I
≤I
]=E
[e
-(B
e
---X
-(ξ
-θ)A
e
)
×I
---≥-×I
----I
≤I
]
。为了让上式取非零值,上述示性函数中的所有事件都必须发生。
当事件
{ηB
e
--<X
}
和
{X
<B
e
---(ξ
-θ)A
e
}
同时发生,则有
ηB
e
--<B
e
---(ξ
-θ)A
e
}
,从而得出
(r
-v)τ
>lnC(r)
。结合τ
≤T
和r>v
,可得τ
的区间为
显然,必须满足约束条件

事件
{ηB
e
--<X
}
和
{X
<B
e
---(ξ
-θ)A
e
}
同时发生等价于
ηB
e
--<X
e
1<B
e
---(ξ
-θ)A
e
}
。把上式先除以X
,
然后两边取自然对数得到Z
1的定义域。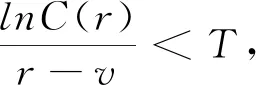

p
=
0。根据式(
18)
计算p
,p
=E
[e
-S
(T)I
I
]=E
[e
-(B
-X
-(A
-θA
e
))
×I
-≥-I
I
I
I
]
。上式取非零值,必须满足
B
-ηB
>B
-X
>A
-θA
e
≥ξA
e
-θA
e
,
这意味着C(v)
必须小于1。由
ηB
<X
=X
e
1<B
+θA
e
-A
≤B
-(ξ
-θ)A
e
,
和
ξA
e
<A
=A
e
2<B
-X
+θA
e
,可得Z
1和Z
2的定义域为
C(v)<
1,则
(D(T,
1,θ)
-X
e
-A
e
)f(z
,z
,T)g(t
,t
)dz
dz
dt
dt
,否则p
=
0。遵循同样的想法,可以推导出p
的表达式。如果C(v)<
1,则
(D(T,
1,θ)
-X
e
-A
e
)f(z
,z
,T)g(t
,t
)dz
dz
dt
dt
,否则p
=
0。p
=E
[e
-S
(τ
)I
≤I
≤]=E
[e
-((
1-η)B
e
---(A
-θA
e
))
×I
1----I
I
≤I
]
。p
的计算和p
相似,为了让上式取非零值,下列不等式必须成立:(
1-η)B
e
-->A
-θA
e
>(ξ
-θ)A
e
。由此得出
(ξ
-θ)A
e
<(
1-η)B
e
--。因为r>v
且τ
≤T,
可以得出约束条件C(r)<
1和(r
-v)τ
>lnC(r),
即
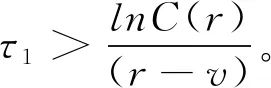
C(r)<
1,则
p
=
0。因为r>v
,所以C(r)>C(v)
。结合所有情况,就得出了结果。定理
2 当无风险利率等于公司债务增长率时(r=v)
,PBGC保险的保费p
如下所示:①如果C(r)=C(v)<
1,则p=p
+p
+p
+p
=


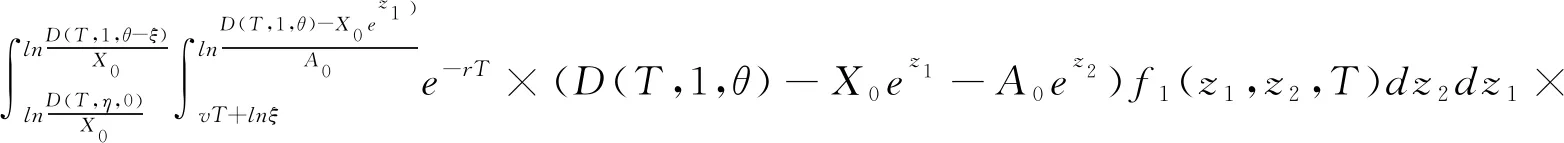

C(r)=C(v)
≥1,则p=
0。定理
3 当无风险利率小于公司债务增长率时(r<v)
,PBGC保险的保费p
如下所示:①如果C(v)<
1,则p=p
+p
+p
+p
=

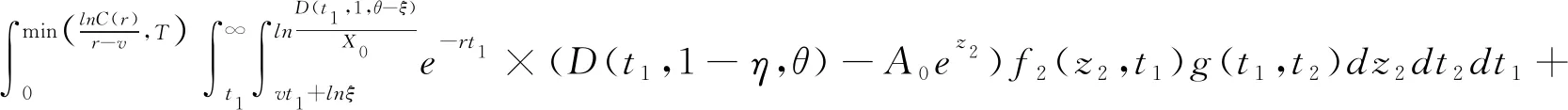


C(v)
≥1且C(r)<
1,则p=p
+p
=


C(v)
≥1,则p=
0。证明类似于定理1。
4 数值模拟与分析



图1 基于风险的保费p与随机通胀波动率σt的关系图 图2 基于风险的保费p与养老基金投资风险资产比例的关系图
5 结论
研究在随机通货膨胀条件得到由PBGC为基于提前和遇险终止风险的DB养老金计划提供担保的保费定价公式,并进行了数值模拟。结果表明,随机通胀的加入使得保费增加了。虽然这一结果给计划发起人增加了负担,需要支付更多的保费给PBGC,但是却降低了PBGC所承担的风险。并且通货膨胀因素在现实中是实际存在的,增加通货膨胀因素大大降低了结果的误差。因为以前的研究没有考虑到通货膨胀,所以前期研究的结果让PBGC实际操作过程中缺少了灵活性。而此处研究结果是在通货膨胀条件下得出的,更符合实际情况,也更容易被PBGC接受。
研究主要的贡献是在同时考虑提前终止和遇险终止的情况下增加随机通胀因素来对PBGC收取的保费进行建模。此外,模型还可以在其他一些方面进行拓展,比如,将固定的无风险利率改进为随机利率。

