双组态柔性重构汽车底盘静力学分析

奚 琳，倪化生，万寿祥，赵 苳，杨 礼

(1.安徽工程大学 机械工程学院，安徽 芜湖 241000；2.中国科学院合肥智能研究所，安徽 合肥 230000)

智能制造2.0时代传统汽车构型的局限与人们多元化需求之间的矛盾日渐显著，以中国人多车多的国情看，目前家用汽车领域主要存在的问题有：上班族一户多车的需求日渐提升，然停车位供给不足；单个人出行与家庭出行时汽车的能源损耗近乎相同。社会问题促发汽车领域对新构型新理论的思考与创新，基于空间可重构技术的汽车研究即将开启。

重构技术指的是根据任务或环境的变化而改变机械的构型，通过模块化柔性组合装配成不同构型的机器以适应不同的工作需求。重构技术多用于机器人领域，涉及模块化、智能化、人机协作、机器增强、环境感知等方面。20世纪80年代Carnegie Mellon University(CMU)研发了世界首台工业用可重构机器人系统,随后，可重构机械在国内外许多领域得以迅速发展。如Braud R等研发了能够动态感知学习的可重构机器人；Ahmad S将重构技术应用于多工况开门机器结构；Oung R将重构技术用于垂直起降型飞行器；Seo J等设计了PolyBot链式可重构机器人；Bhole A等利用重构技术解决了爬梯机构中的悬垂问题；Giusti A等则将可重构技术研究用于机械手的模块化控制；Cordie T P等研制的可重构NeWheel城市搜救机器(USAR)能够在杂乱的建筑和不稳定的地板上完成工作；Manzoor S设计了蛇形可重构机器,对比了不同运动的特性；Motzki P设计了热熔合金可重构机器；Baca等研究的ModRED动态重构机器设备对探索与发现工作进行了仿真分析。中国航天科技集团有限公司空间结构与机构技术实验室设计了一种抱爪式对接机构，采用异体同构周边式构型对捕获缓冲系统进行了动力学分析。

基于重构技术的柔性设计正在各制造领域有力缩短了设计周期，快速应对市场变化需求。研究将重构理论作用于汽车领域，提出两车变一车(4座变8座)的新构型模块化组态汽车。基于视觉跟随技术的三点圆周边环锥式对接机构实现主动车体找寻目标车体，通过弱碰撞大容差的对接过程，捕获成功成为空间扩容的组合型车体，并且主动车与目标车也可以分别作为独立的微型车行驶。双微型车解决了一户多车的需求，同时节省了能源。组合整车只占据一个停车位，解决了停车难的问题。介绍了双驱动双组态车体的柔性重构模块化原理，针对重构车身连接处关键零部件做了不同行驶工况下的静力学分析，验证新车型的安全性能。

1 重构汽车结构模型

1.1 重构汽车建模

主动车与目标车均为可独立行驶的微型车，此为第一组态；而重构后的整车将实现空间扩容，实现第二组态。两车尾门采用平开模式，由气泵驱动顶部曲柄滑块机构实现车门朝内折叠，尾门4座椅展开即构成8座大车，实现空间重组，建模如图1所示。

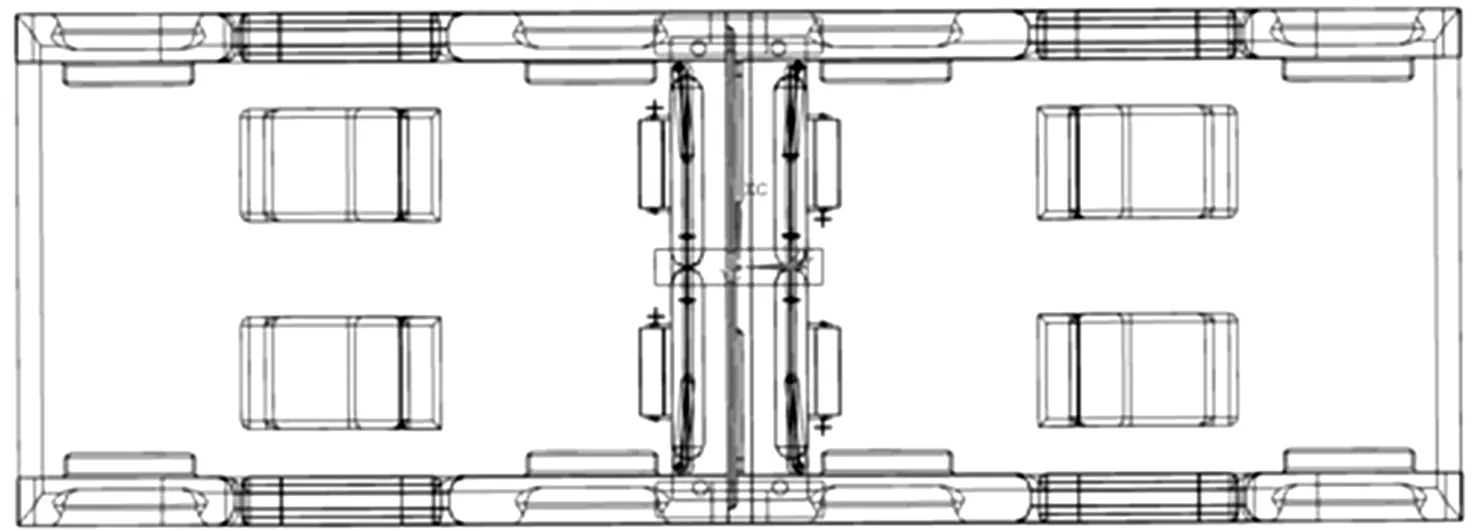
图1 重构汽车结构图

双车对接是指主动车体在无人驾驶模式下一键找寻目标车体。建立了由人工信标、视觉模块、嵌入式图像处理平台组成的视觉定位系统，设计了“三点圆-周边环锥式”对接结构，通过空气悬架辅助完成位姿调整与弱碰撞对接过程，底盘结构如图2所示。

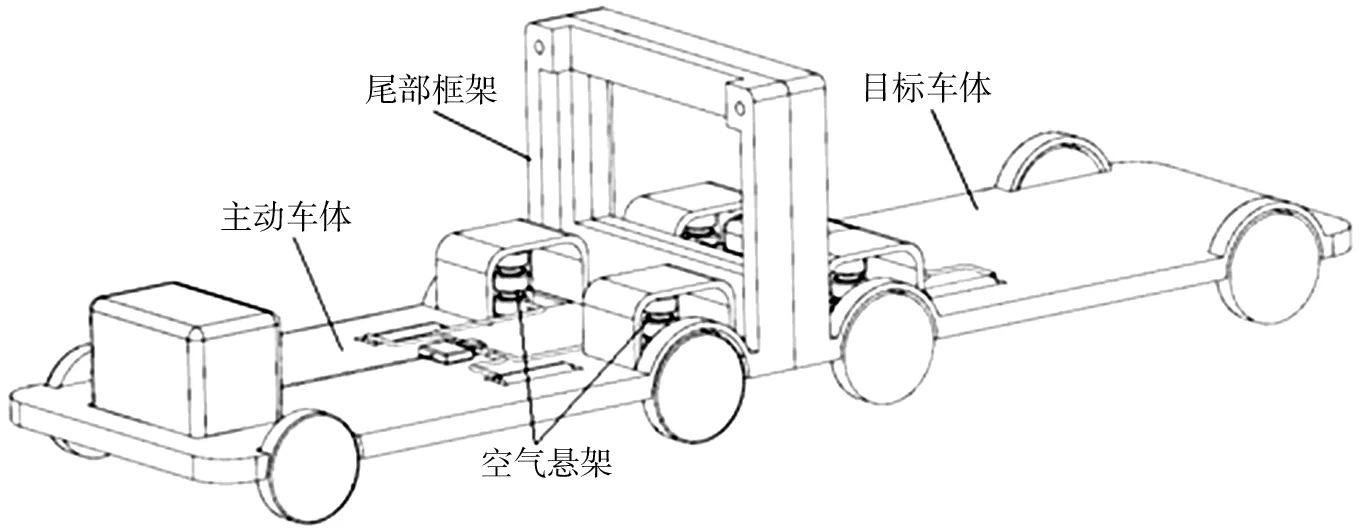
图2 重构汽车底盘对接结构图

1.2 底盘对接机构模型

底盘作为整车的支撑，用以支承、安装汽车发动机和其他各部件、总成，在底盘上设置有转向控制装置、制动控制装置和减震缓冲装置，以确保车辆能够正常行驶。底盘设计兼顾汽车操纵稳定性、行驶平顺性、乘坐舒适性、转向自如性、制动安全性和底盘的紧凑性等各方面综合性能。在常规道路驾驶时，底盘结构应能够提供良好的舒适性、减震和隔音性能；在路况较差的道路行驶时，底盘结构的动力、传动、悬架、制动和转向响应要迅速；高速行驶时，底盘结构应能提供较低的重心和更好的稳定性。

双驱动双组态重构汽车的底盘强度验证尤为重要，需要针对各种行驶工况做静力学计算。对接机构中涉及底盘部分的关键零部件是柔性驱板机构，当视觉跟随系统完成定位后触发对接机构，底盘柔性驱板机构由液压系统驱动沿线性导轨滑入锁槽，由锁舌销插入锁紧，模型如图3所示。

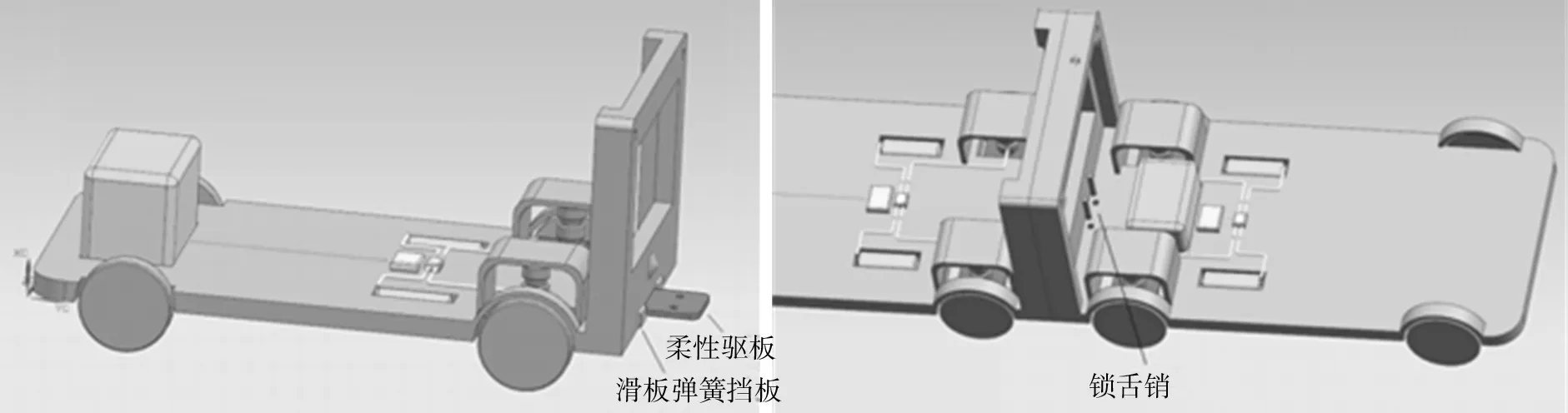
图3 主动车底盘柔性驱板机构模型

2 运动系参数

2.1 车身参数设定

为车身建模首先要确定车身基本参数，参照常规车型参数范围，设定车身基本参数如表1所示。

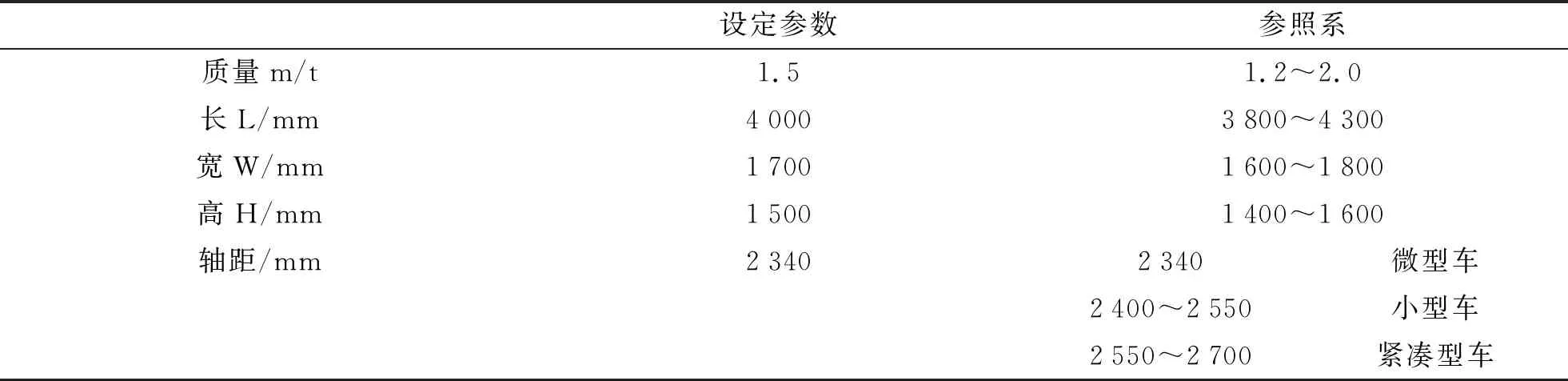
表1 车身参数

2.2 行驶条件拟定

假定汽车在坡度6°的良好路面上，在40 km/h的初速度下，以1 m/s的加速度II档加速行驶，设汽车行驶的空气阻力为

F

，滚动阻力为

F

，坡度阻力为

F

，加速度阻力为

F

。∑

F=F

+

F

+

F

+

F

,

(1)

空气阻力无风时有：

(

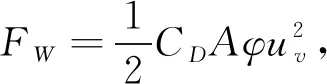
2

)

取空气阻力系数

C

为0.3

;

逆风面积

A

为1.7

;φ

为空气密度，一般取

φ

=

1.225 8

kg

/

m

；

u

为相对速度。由式(2)可得

F

=

500.126 4 N。

滚动阻力：

F

=W

·

f,

(3)

式中，

W

为本车负荷；

f

为滚动阻力系数，在良好的沥青或混凝土路面上

f

的取值范围在

[

0.01，0.018

]

，取

f=

0.014。由式(13)可得

F

=

182 N。

坡度阻力：

F

=G

sin

α,

(4)

因为一般道路坡度较小，所以

sinα

≈

tgα

≈

i

，

F

=G

·

i=

1 401.4 N。

加速度阻力：

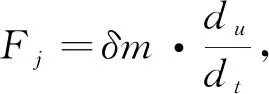
(5)

其中，

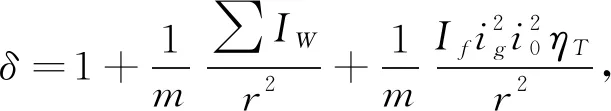
(6)

二档加速时，

δ

取1.15，代入式(5)得

F

=

1 495 N。将以上所得代入式(1)：∑

F=F

+

F

+

F

+

F

=

4 878.526 4 N。

两车重构后，主动车对被动车施加总力为

F

=

∑

F

+

ma

，取

F

=

5 000 N。

3 载荷工况

3.1 加速工况行驶

双组态汽车在组合形态下，在加速工况行驶时(见图4)，主动车作为动力来源，柔性驱板的两侧限位面受限位块挤压力而引起微量压缩，根据查阅相关汽车的相关参数得知，汽车的最大加速度

a

不超过

g

(即

a

≤

g

)。此处分析极限运动状态

(a=g)

时的受力情况如图4所示。由牛顿第二定律得

F=

15 000 N。由于在两侧相同的挤压面都有作用力，因此单个挤压表面受力约为

F

=F

=

0.5

F=

7 500 N。

3.2 减速工况行驶

双组态汽车在组合形态下，在减速工况下行驶时(见图5)，主动车撤去动力来源，柔性驱板的最后面受底盘后下方空腔内面挤压力而引起微量压缩。根据查阅相关汽车的相关参数得知，汽车的最大减速度

a

不超过0.5

g

(即

a

≤0.5

g

)。此处分析极限运动状态(

a=

0.5

g

)时的受力情况如图5所示。由牛顿第二定律得

F=

7 500 N。因此，挤压表面受力约为7 500 N。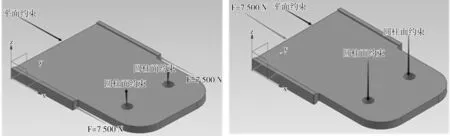

图4 加速工况行驶极限运动状态时柔性驱板的受力图 图5 减速工况行驶极限运动状态时柔性驱板的受力图

3.3 横向碰撞工况

双组态汽车在组合形态下，在横向碰撞工况时(见图6)，主动车作为动力来源，柔性驱板的左右两侧面受底盘后下方空腔内面和T型槽面挤压力而引起剪切。根据查阅相关汽车的相关参数得知，汽车横向碰撞时的最大加速度

a

不超过0.5

g

(即

a

≤0.5

g

)。此处分析极限运动状态

(a=g)

时的受力情况如图6所示。由牛顿第二定律得

F=

7 500 N，由于在两侧的挤压面有一对方向相反作用力，因此，单个挤压表面受力约为7 500 N。

3.4 弯道工况行驶

双组态汽车在组合形态下，在弯道工况行驶时(见图7)，主动车作为动力来源，柔性驱板的一侧后方最后面受底盘后下方空腔内面挤压力而引起微量变形，根据查阅相关汽车的相关参数得知，汽车的最大弯道加速度

a

不超过0.3

g

(即

a

≤0.3

g

)。此处分析极限运动状态

(a=g)

时的受力情况如图7所示。由牛顿第二定律得

F=

4 500 N，挤压表面受力约为4 500 N。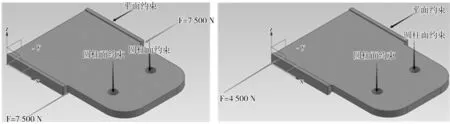

图6 横向碰撞工况时柔性驱板受力图 图7 弯道工况行驶极限运动状态时柔性驱板受力图

3.5 颠簸工况行驶

双组态汽车在组合形态下，在颠簸工况行驶时(见图8)，主动车作为动力来源，柔性驱板的后侧上方受底盘后下方空腔内面挤压力而引起微量变形。根据查阅相关汽车的相关参数得知，整个车体脱离地面，汽车颠簸时最大加速度

a

不超过

g

(即

a

≤

g

)。此处分析极限运动状态

(a=g)

时的受力情况如图8所示。由牛顿第二定律得

F=

15 000 N，由于在两侧相同的挤压面都有作用力，因此单个挤压表面受力约为7 500 N。

4 静力学分析

车架的材料选择为45号钢，密度为7 890，弹性模量为209 000 MPa，泊松比为0.269。利用ANSYS Workbench为底盘对接机构进行应力分析，主要分析柔性驱板的受力情况，通过进行线性静力分析来验证它在不同工况运动过程中是否安全可靠。柔性驱动板在不同工况下可能会出现伸张状态或压缩状态，分析时加入相应载荷，对模型进行网格划分，应用网格控制选取分析面，设置网格密度，分别得出分析元件的应力、应变分析图。

4.1 加速工况行驶

将在UG中已经画好的柔性驱板模型导入ANSYS Workbench中，然后将柔性驱板进行网格划分，点击Mesh和Update调整下方的Sizing，再点击Proximity and Curvature，网格自动划分在较为重要的位置和表面。将网格适当缩小以使结果更加准确。点击Update，得到的结果如图9所示。

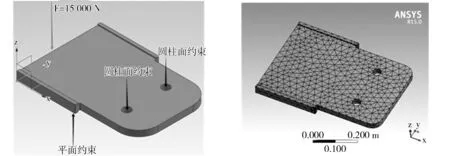
图8 颠簸工况行驶极限运动状态时柔性驱板受力图 图9 柔性驱板网格划分图

在网格划分后的柔性驱板选取分析面，点击Supports选项中的Fixed Supports和Cylindrical Supports，然后给被动车体施加加速力，点击Loads中选用Force，最大作用力7 500 N，如图10所示。

图10 加速工况行驶时受力示意图

加速工况行驶时应变云图如图11所示。由图11可以看出，柔性驱板的应变从两侧中间拐角处向端部递减，而驱板根部应变趋于零。加速工况行驶时应力云图如图12所示。由图12可以看出，柔性驱板的两侧中间拐角处应力呈小范围波纹状集中分布迅速递减，应力范围在[1.25,10]MPa，驱板整体所受应力趋于零。

4.2 减速工况行驶

由于ANSYS Workbench软件具有参数共享性，分析步骤同加速工况行驶时应力分析的步骤，只需更改分析面的受力方向和大小。在网格划分后的柔性驱板选取分析面，点击Supports选项中的Fixed Supports和Cylindrical Supports，对被动车体施加减速力，点击Loads中选用Force，最大作用力7 500 N，如图13所示。得到施力图、应变云图和应力分布云图分别如图13、图14、图15所示。由图13、图14、图15可以看出，柔性驱板应变由根部呈梯度向端部递减，锁舌销及端部应变趋于零。通过应力云图可看出柔性驱板从根部到锁舌销部位，应力分布均匀，约为0.75 MPa，端部应力分布范围在[0.002，0.18]MPa。

4.3 横向碰撞工况

给柔性驱板施加横向碰撞力，点击Loads中选用Force，最大作用力7 500 N，如图16所示。得到的施力图、应变云图和应力分布云图分别如图16、图17、图18所示。由图16、图17、图18可知，柔性驱板应变由根部单侧向周边呈波纹状递减，最大值仅0.002 mm，端部对角线应变约为0.000 47 mm，中部应变趋于零。通过应力云图可看出柔性驱板应力大面积集中于根部和中部，应力范围约在[0.28,1.1]MPa。

图11 加速工况行驶时应变云图 图12 加速工况行驶时应力云图

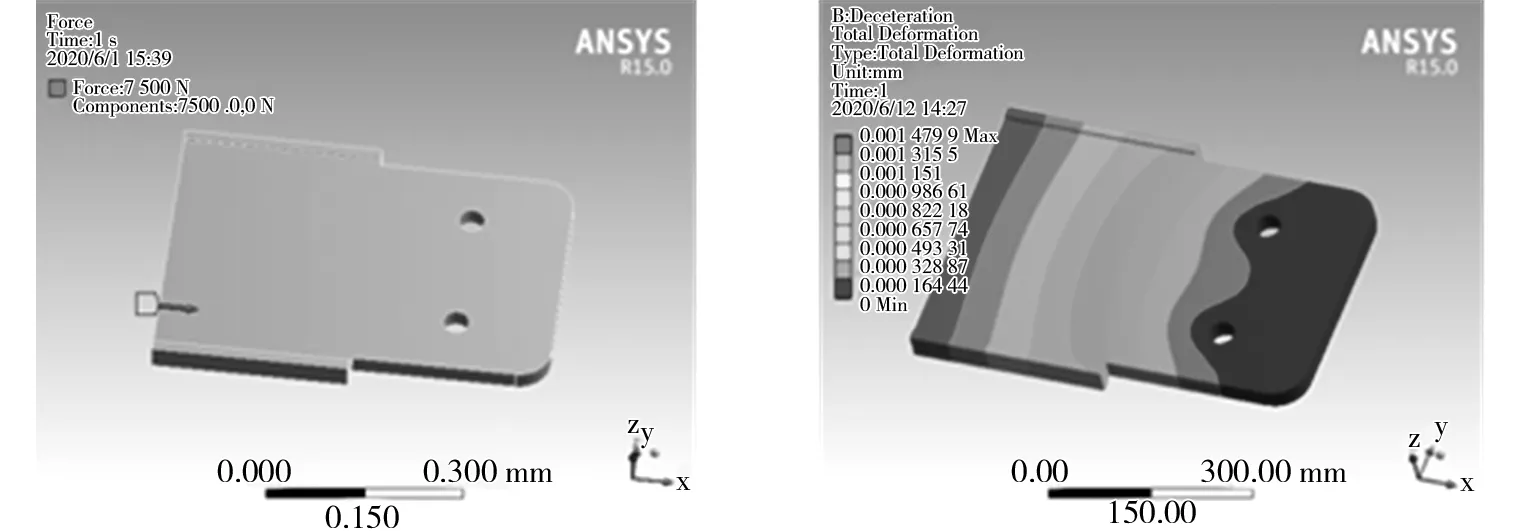
图13 减速工况行驶时受力示意图 图14 减速工况行驶时应变云图

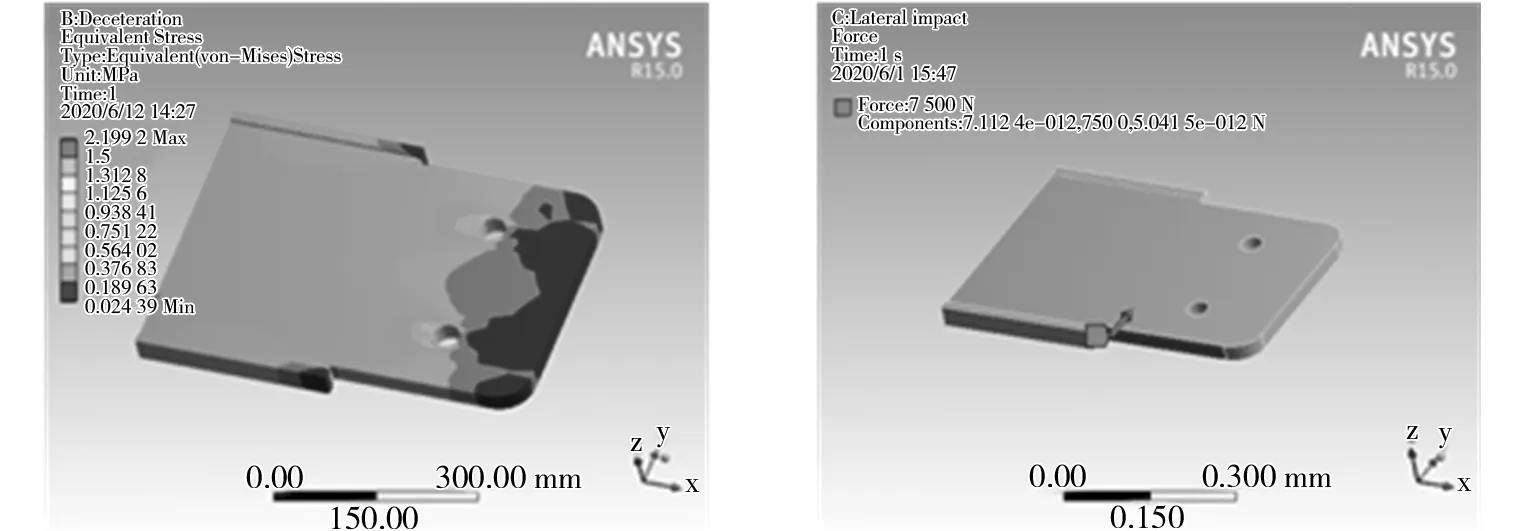
图15 减速工况行驶时应力云图 图16 横向碰撞工况时受力示意图

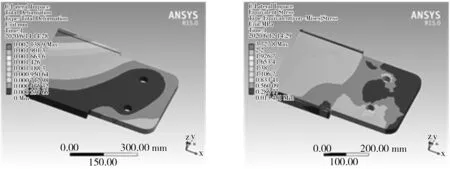
图17 横向碰撞工况时应变云图 图18 横向碰撞工况时应力云图

4.4 弯道工况行驶

给柔性驱板施加一个弯道驱动力，最大作用力4 500 N。得到的施力图、应变云图和应力分布云图分别如图19、图20、图21所示。由图19、图20、图21可知，柔性驱板应变由弯道根部单侧向周边呈波纹状递减，最大值仅0.004 7 mm，驱板弯道同侧端部应变仅约0.000 75 mm，驱板整体应力趋于零。通过应力云图可看出柔性驱板应力同样由弯道根部单侧向周边呈波纹状递减，最大应力呈点状集中，约为8 MPa。

4.5 颠簸工况行驶

给柔性驱板施加上下颠簸力，点击Loads中选用Force，颠簸力最大为15 000N。得到的施力图、应变分布云图和应力云图分别如图22、图23、图24所示。由图22、图23、图24可知，柔性驱板应变由根部中心向周边呈波纹状递减，最大值达0.056 mm，中部应变趋于零，端部应变较小，约以0.037 mm向中心递减。通过应力云图可看出柔性驱板应力以根部和近端部向中部呈梯度递减，最大应力约为6.25 MPa。

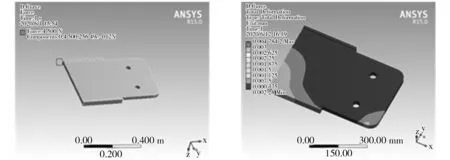
图19 弯道工况行驶时受力示意图 图20 弯道工况行驶时应变云图

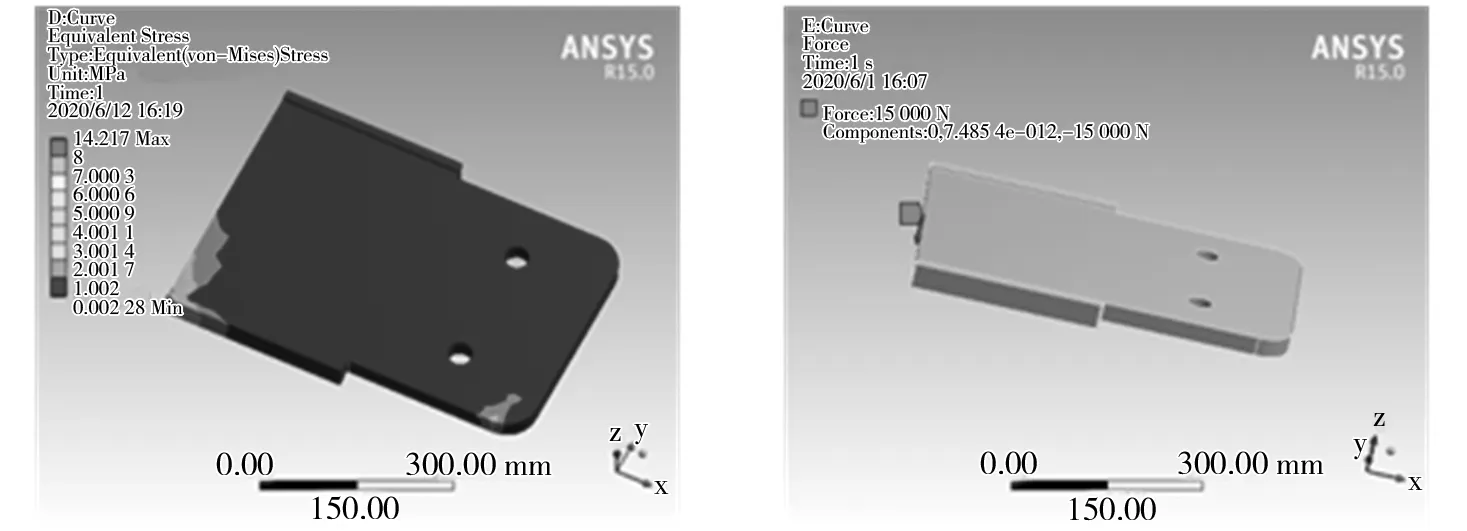
图21 弯道工况行驶时应力云图 图22 颠簸工况行驶时受力示意图

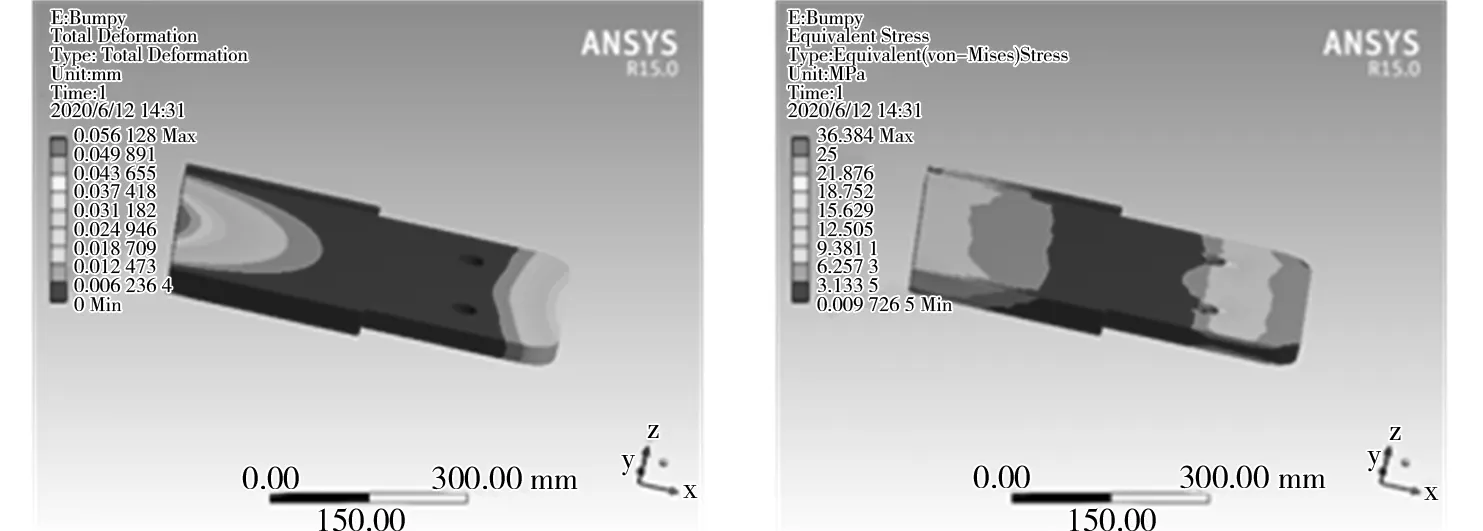
图23 颠簸工况行驶时应变云图 图24 颠簸工况行驶时应力云图

5 结论

基于可重构技术设计了双组态汽车车身构型，实现了双车与整车正逆向的空间重组行为。从车身安全性角度考虑，利用有限元法重点分析了底盘对接核心零部件-柔性驱板的强度情况。针对上述5种行驶工况，柔性驱板的应力应变分析结果表明，指标均远低于强度极限，论证了重构汽车的安全性和可靠性，为智能制造下新车型开发提供了创新思路。