一维正弦混沌系统及S盒设计

郝俊灵

(厦门大学嘉庚学院 信息科学与技术学院，福建 漳州 363105)

0 引言

在许多分组密码的算法中，S盒是唯一的非线性部分，对于分组密码的安全性起着非常重要的作用。因此，构造性能优良的S盒成为重要的研究课题，受到广大学者的关注[1-3]。

混沌系统是一个具有初值敏感性、伪随机性、不可预测性等性质的非线性系统[4]。因此，利用混沌系统构造S盒，成为许多密码学研究者的重要研究方向[1，5-7]。文[1]和[7]均是利用混沌Lorenz系统设计S盒，混沌Lorenz系统属于高维混沌系统，拥有多个可以设计为密钥的参数，但是因其维数较高，所以计算速度比低维混沌系统慢。文[2]利用Tent混沌映射构造S盒，通过使用多重映射，使得构造S盒所需要的迭代次数较少。文[7]给出了一种基于两级Logistic映射的S盒构造算法。

受上述文献的启发，本文通过正弦函数和Logistic混沌映射的复合，构造了一个新的低维混沌映射，然后基于该混沌系统提出S盒的构造方案。相对于传统的一维Logistic混沌映射，该混沌系统不仅保持了低维混沌系统的计算速度快、效率高的特点，而且通过其分岔图和李亚普诺夫指数分析，可以证实本文提出的混沌系统(以下简称“本文系统”)不但具有较大的密钥空间，而且很好地弥补了传统Logistic混沌映射存在周期窗口的缺点。最后通过对S盒的非线性度、严格雪崩准则(SAC)、比特间独立性准则分析，说明该算法生成的S盒性能优良，可以应用于加密系统。

1 混沌系统及其动力学特性分析

1.1 混沌系统

传统的Logistic混沌系统定义如下[7-8]:

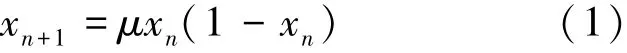
式(1)中:控制参数μ∈(0，4]、初始值x0∈(0，1)，当μ∈(3.57，4]时，系统表现出混沌行为。从μ和x0的取值能够明显看到该混沌系统的密钥空间取值范围比较小。为提升密钥空间，本文通过正弦函数和Logistic混沌映射的复合，获得如下正弦混沌映射:

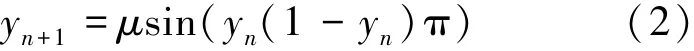
式(2)中:μ∈(-∞，+∞)，且μ≠0，初始值y0∈(0，1)。

1.2 动力学特性分析

图1 传统Logistic映射的李亚普诺夫指数图

为了证实混沌系统(2)(即“本文系统”)的密钥空间远大于传统的Logistic混沌系统的密钥空间，具有更好的密码学特性，下面给出该系统的李亚普诺夫指数图和分岔图。图1和图2分别为传统Logistic映射和本文系统的李亚普诺夫指数图。图3和图4分别为传统Logistic映射和本文系统的分岔图。通过李亚普诺夫指数图和分岔图对比，易见Logistic混沌系统的混沌区间较小，且其分岔图含有周期窗口，而本文系统混沌区间较大且无周期窗口，从而极大提升了密钥空间，若应用到加密系统，会具有比较高的安全性。

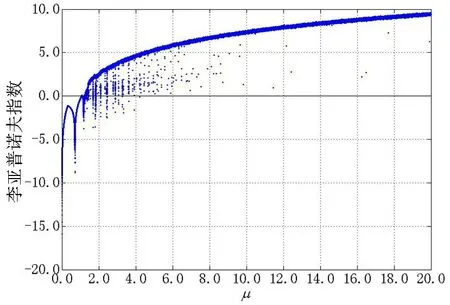
图2 本文系统的李亚普诺夫指数图

图3 传统Logistic映射分岔图

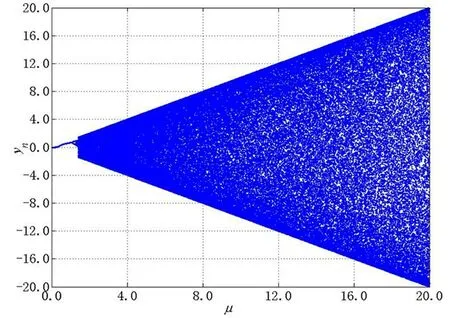
图4 本文系统的分岔图

2 S盒构造方法及性能分析

为了说明本文系统可以应用到加密系统，下文将借助于该混沌系统构造S盒，同时对获得的S盒的相关安全性能进行分析。

2.1 S盒的构造算法

下面给出输入和输出均为8比特的8×8 S盒设计方案:

步骤1 设置正弦混沌映射的参数μ的值及系统初值y0。

步骤2 迭代方程正弦混沌映射N次获得混沌序列值y1，y2，…，yN。为消除初态效应，删除该序列前1000个数值，获得序列Y。

步骤3 计算序列值

即获得序列Z。

步骤4 剔除序列Z中所有重复的数据后，获得各项取值均不相同的序列X:x1，x2，…，xk。

步骤5 若k＜256，则迭代正弦混沌系统第N+1次，按照步骤3和步骤4的方法更新序列X直到k=256。从而获得S盒。

按照上述方案，取y0=0.25，μ=3.26， 即得表1中的S盒。

表1 本文构造的S盒

2.2 S盒的安全性能分析

为了证实用本文系统构造的S盒具有优良的密码学性能，本节将从SAC、非线性度(Nonlinearity)、比特独立性准则(BIC)3个方面分析所构造的S盒的安全性能，从而验证本文系统用于S盒构造的可行性。

SAC是指布尔函数的一个输入比特发生改变时，一半的输出比特会发生改变。分析S盒是否满足SAC，只需把S盒看作一个布尔函数即可，当SAC接近理想值0.5时，说明所构造的S盒满足SAC。文[9]首次提出SAC，并给出一种测试S盒是否满足SAC的方法。按照文[9]提出的方法，使用软件Matlab2014a计算本文及其他文献所构造的S盒的SAC，其结果见表2。

表2 S盒性能分析

非线性度的大小可以反映S盒抵御线性攻击的能力。为了有效抵御线性攻击，一个安全有效的S盒的非线性度必需充分大。S盒可以看作一个布尔函数f(x)，其非线性度的计算需要借助于Walsh谱，具体计算公式如下[12]。

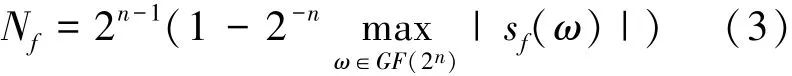
式(3)中f(x)的Walsh谱

这里ω∈GF(2n)，x·ω=x1·ω1⊕…⊕xn·ωn。

文[9]提出S盒的BIC，作为评价S盒性能的一个重要指标，良好的比特间独立性，可以有效地抵抗外界对密码系统的攻击。S盒可以看作函数g其BIC计算公式如下。

根据式(3)和(4)，使用软件Matlab2014a分别对S盒的非线性度和BIC进行计算，其结果见表2。由表2的数据可见，本文构造的S盒的SAC平均值为0.500 0，已达到理想值，结果优于文[8]和[10]。本文构造的S盒的非线性度的最小值、平均值及最大值均与文[6，8，10]相当；而文[11]的非线性度数值虽然优于本文提出的S盒，但是其所用的混沌系统是具有周期窗口的，存在安全隐患。此外，本文构造的S盒的BIC也与文[6，8]相当。综上，本文系统及S盒性能优良，适用于设计加密系统。

3 结语

本文构造了一个新的正弦混沌系统，并通过仿真分析证实该混沌系统具有良好混沌特性。然后，基于该混沌系统给出S盒的构造算法。最后，通过对所构造的S盒进行安全性能分析，结果表明本文构造的S盒性能优良，可以用于设计加密系统。