基于杆系单元某独塔斜拉桥静动载检测试验的实例分析
邵森泉 (合肥市市政设计研究总院有限公司,安徽 合肥 230000)
1 工程背景
本工程实例上部结构为(90+110)m斜置拱塔双索面预应力混凝土斜拉桥,塔、梁、墩固结体系,主梁采用双主梁肋板式结构形式,锚跨压重区域主梁截面采用箱型截面,全长205m,全宽40m,标准横断面为:0.25m(栏杆)+2.25m(人行道)+3.5m(非机动车道)+3m(隔离带)+22m(机动车道)++3m(隔离带)+3.5m(非机动车道)+2.25m(人行道)+0.25m(栏杆)=40m,道路等级为城市主干道Ⅲ级,荷载等级为公路-Ⅰ级;下部结构为主墩基础采用承台灌注群桩基础,承台顶设1.5m高塔座。桥台采用桩柱式台、钻孔灌注桩基础。
2 理论分析
进行荷载试验前,根据设计资料,使用有限元分析软件Midas Civil 2020建立模型,全桥共169个节点,211个梁单元,68个只受拉桁架单元,支座处采用弹性连接模拟,计算桥梁结构在不同试验工况作用下控制的应变、应力和位移理论值。模型如图2所示。

图1 桥梁现场照片

图2 有限元分析基础模型
3 静载试验
3.1 试验工况
根据桥梁结构形式、业主要求及现场调查发现的桥梁施工质量缺陷确定试验工况如表1所示。

试验工况一览表 表1
挠度测点布置在桥梁控制截面底缘处,测点布置见图3。
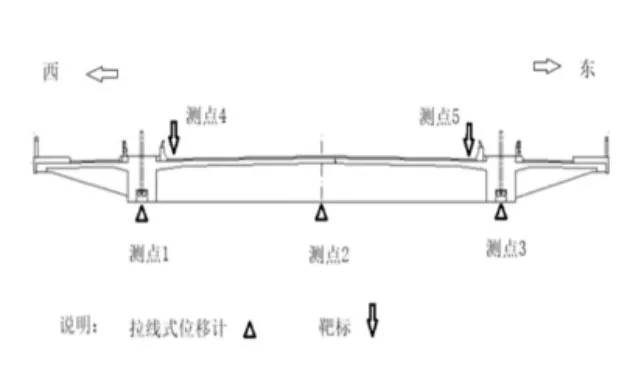
图3 挠度位移测点布置
本桥梁静载试验共布置5个挠度位移测点,分别为梁底f1、f2和f3,桥面f4和f5。
塔顶偏位选择使用全站仪进行各测点的偏位测量。为测得在试验荷载作用下,该桥塔顶最大侧移分级变化过程,偏位控制测点设置在塔顶处。测点布置见图4。
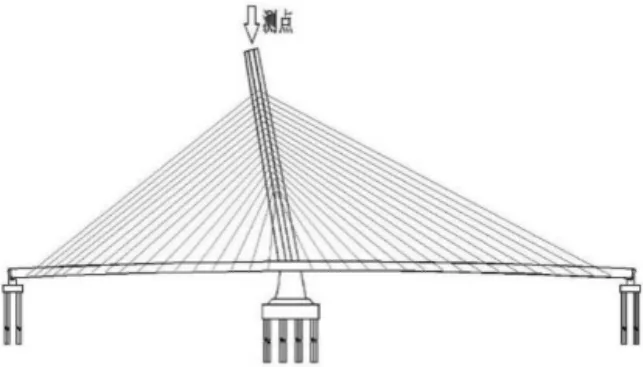
图4 塔顶最大偏位测点布置图
在本桥梁最大正弯矩控制截面梁底缘各布置3个表面应变计,分别位于双主梁与横肋处,应力测点布置见图5。

图5 应变测点布置
塔身最大弯矩控制截面设在塔梁固结处,主塔与桥梁铺装层搭接处布置2个测点,测点布置见图6。

图6 塔身截面弯矩应力测点布置图
车辆横向布置图见图7及图8。
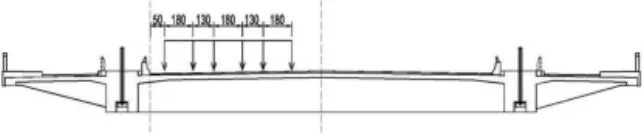
图7 车辆偏载横向布置图(单位:cm)
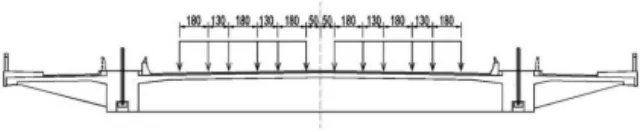
图8 车辆对称加载横向布置图(单位:cm)
本次静载试验过程中,应变采用DH3816应变采集仪进行应变实时采集,沉降位移采用拉线式位移计和挠度仪进行测量。
3.2 静载试验评定结论
静载试验主要是通过结构校验系数、相对残余变形或相对残余应变等数据对结构工作状况进行评定。
根据表2及图9~图12可知,各工况作用下应变校验系数在0.36~0.88之间,变形校验系数在0.53~0.74之间;相对残余应变在0.1%~15.8%之间,相对残余变形在3.20%~10.20%之间,说明桥梁处于弹性工作状态以及具有一定的安全储备。

索力评定表 表2
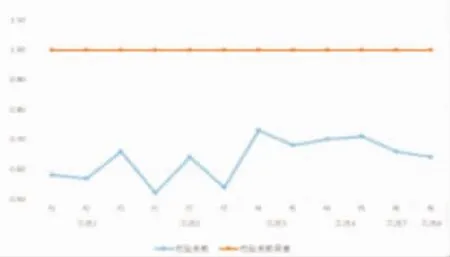
图9 变形校验系数曲线

图10 相对残余变形曲线

图11 应变校验系数曲线

图12 相对残余应变曲线
4 动载试验
4.1 布置拾振传感器
本桥根据振型的特点,在振型的峰、谷位置布置相应传感器。主要布置在每跨八等分处。每跨共分别布置7个拾振传感器。见图13。

图13 拾振器布置图
4.2 动载试验结果
4.2.1 跑车试验
在桥面无任何障碍的情况下,用2辆载重汽车以10km/h、20km/h的速度驶过,并采集运行车辆荷载作用下的动力特性。图14~图15为车速10km/h和20km/h跑车曲线。

图14 10km/h跑车曲线
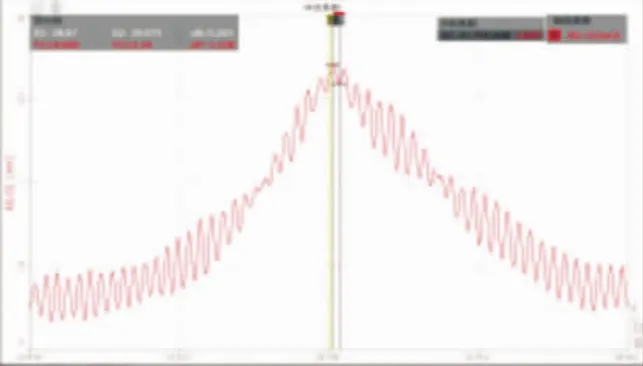
图15 20km/h跑车曲线
4.2.2 刹车试验
在桥面无任何障碍的情况下,用2辆载重汽车以10km/h和30km/h的速度驶至测试截面进行刹车,并采集运行车辆荷载作用下的动力特性。图16~图17为车速10km/h和30km/h刹车曲线。
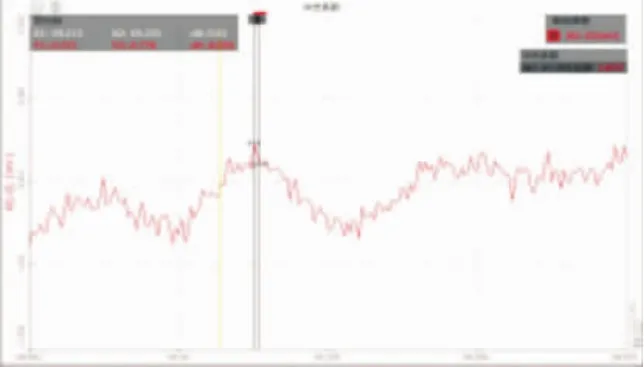
图16 10km/h刹车曲线
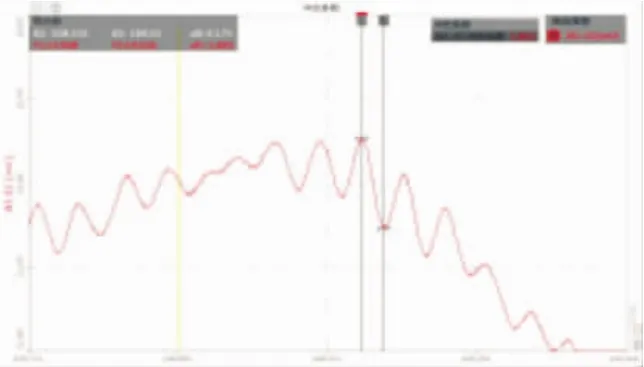
图17 30km/h刹车曲线
4.2.3 动挠度测试结果
4.2.3.1 跑车试验
在桥面无任何障碍的情况下,用2辆载重汽车以10km/h、20km/h的速度驶过,并采集运行车辆荷载作用下的动力特性。图18~图19为车速10km/h和20km/h跑车曲线。
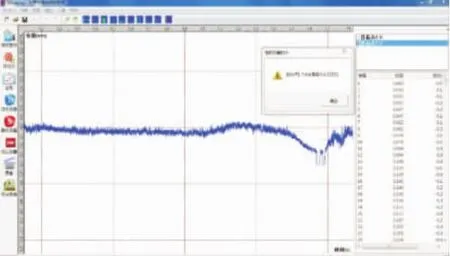
图18 10km/h跑车曲线
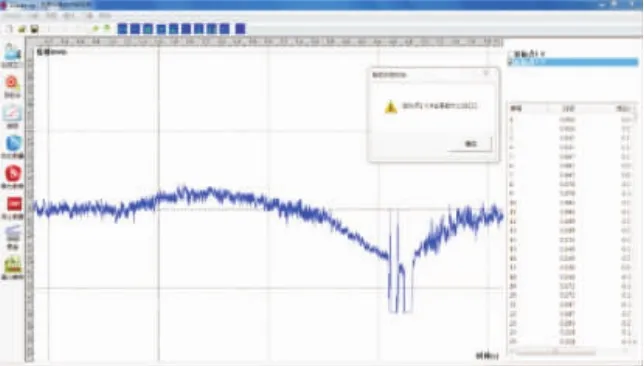
图19 20km/h跑车曲线
4.2.3.2 刹车试验
在桥面无任何障碍的情况下,用2辆载重汽车以10km/h和30km/h的速度驶至测试截面进行刹车,并采集运行车辆荷载作用下的动力特性。图20~图21为车速10km/h和30km/h刹车曲线。
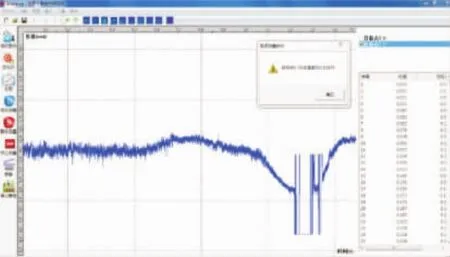
图20 10km/h刹车曲线

图21 30km/h刹车曲线
4.2.4 自振特性测试结果
4.2.4.1 信号采集与分析
采用连续采样方式在自然环境激励作用下采集拾震器的速度响应信号,每通道的采样率设为:100Hz,采样时间一般每个批次尺寸约15~20min。
通过时域平均、频域滤波等方法对信号去噪,利用收集信号的互谱、自功率谱、相干函数识别桥梁竖向振动的前三阶模态参数。该桥理论及实测振型见图22~图27所示。

图22 理论一阶频率及振型(f1=0.892Hz)

图23 实测一阶频率及(f1=1.172Hz)

图24 理论二阶频率及振型(f2=1.030Hz)

图25 实测二阶频率及振型(f2=1.953Hz)

图26 理论三阶频率及振型(f3=2.108Hz)

图27 实测三阶频率及(f3=2.832Hz)
根据实测结果与理论计算对比结果,桥梁前三阶理论自振频率均小于实测自振频率,说明桥梁结构各部件整体性能和技术状况较好。
5 静动载试验问题与建议
根据上述静动载试验结论可知,理论计算模型与试验结果相结合,能够较好地反映结构现有的技术状态,尤其是墩塔梁固结的斜拉桥,基于有限元分析相对准确,但是误差还是存在,在工程实际运用中,仿真分析又显得繁琐与不简便,因此从数据的贴合度与精确性上来说,满足工程使用。
笔者下一步尝试基于构件分析该斜拉桥数据分析,与实际检测数据以及基于杆系单元分析的结果进行比较,在满足工程实用与理论精确的临界点寻求和谐统一。

