考虑源荷互动的主动配电网两层优化调度

文 达，崔双喜，樊小朝，降国俊

新疆大学 电气工程学院，乌鲁木齐830047

随着环境污染和能源枯竭的问题日益凸显，风力发电、光伏发电等清洁能源在政府扶持下得到了快速的发展。然而清洁能源具有明显的随机性和时序性，将其并网后会增大配电网的调度压力，从而产生弃风、弃光的能源浪费问题。

负荷侧多元化的发展趋势为负荷参与主动配电网（Active Distribution Network，ADN）清洁能源消纳提供了可能性[1]。柔性负荷作为一种新的可调度资源，极大缓解了ADN 的调度压力，同时可以为清洁能源消纳和负荷削峰填谷提供良好的支撑作用[2]。文献[3]根据分时电价将负荷侧分为可转移负荷和可中断负荷，以负荷的调整功率、机组发电功率为决策变量建立ADN 优化调度模型，优化了系统的经济运行成本。文献[4]提出了基于节点电价概念的最优潮流模型，并通过跟踪中心点轨迹内点法对模型求解，算例证明电价响应下的柔性负荷能够有效地提高风电的消纳率。文献[5]研究了基于激励响应形式的柔性负荷对配电网运行可靠性的影响。文献[6]提出了激励响应模式下可削减负荷补偿代价模型，并设计了四种源荷联合调度模式进行验证，仿真结果表明可削减负荷能够有效减小系统运行成本，改善负荷曲线。这些文献考虑了柔性负荷单一调度形势下与ADN 中其他可调度资源的良性互动，但忽略了不同调度形式下柔性负荷在时空上的耦合性以及其与清洁能源互动的可能性。此外，在ADN 制定优化调度方案时，大多数文献都是采用多目标优化调度模型来解决多个优化目标函数的问题[7-9]。如文献[10]通过层次分析法计算多目标优化问题中各子目标权重占比构造综合单目标函数。文献[11]引入模糊模型，将模糊非线性多目标优化问题转化为单目标问题进行求解。以上方法虽然解决了多目标优化求解难的问题，但求解过程复杂，且互有博弈关系的目标函数之间难以协调，不能满足ADN对尽可能消纳风光发电前提下优化系统综合运行成本的要求。

针对上述情况，为了充分挖掘柔性负荷的调度潜力，提高清洁能源的消纳率，本文建立了一种计及源荷协调互动的两层优化调度模型。首先，根据负荷参与电网调度形式不同将负荷分为刚需负荷、可转移负荷、可控制负荷并分别建立响应模型，在负荷层通过两种柔性负荷与清洁能源的协调互动优化负荷曲线以及清洁能源出力曲线，使两者在变化趋势上相契合；主动配网层则从经济性角度出发，通过建立最小化综合运行成本调度模型对配网内分布式能源出力进行调度；最后，提出禁忌-细胞膜优化算法（Tabu Search-Cell Μembrane Optimization algorithm，TS-CΜO）对模型求解，通过算例对比分析了分层前后、负荷分类前后三种方案下的优化调度结果，证明了提出的优化调度模型对提高清洁能源消纳率和降低负荷峰谷差的有效性、可行性。

1 负荷层

随着智能电网日益发展，大量柔性负荷、清洁能源接入配电网，传统的优化调度模型在提高清洁能源利用率、降低负荷峰谷差等方面已经不再具有优势。因此，为了深度挖掘负荷侧可调度资源，本文建立考虑分类负荷的源荷协调互动优化调度模型。

1.1 负荷响应分类建模

国内外专家对柔性负荷参与电网调度的形式已有不少研究，在我国配电网中最常见的有基于电价响应的形式和基于激励响应的形式[12]。本节将ADN内的负荷按照调度形式不同分为不参与调度的刚需负荷、基于电价响应形式的可转移负荷、基于激励响应形式的可控制负荷。

（1）基于电价响应的可转移负荷

基于电价响应的可转移负荷是指一些在用电时段上可以灵活选择的负荷，如电动汽车充电站、居民用户和小型商业用户等分布分散、单体容量小且控制数量众多的用电用户，通过合理的分时电价引导，可以有效地调节负荷的用电时段。对可转移负荷建模如下：

基于电价响应的调度形式通过电价信号引导用电负荷合理调节用电结构和用电方式[13]，本节基于负荷的电量电价弹性需求理论，以制定峰谷平分时电价的方式引导用户转移用电负荷，改变柔性负荷在时序上的分布。

（2）基于激励响应的可控制负荷

基于激励响应的调度形式常见项目包括直接负荷控制、可中断负荷和紧急需求响应等，本节通过直接负荷控制技术实现对可控制负荷的削减。可控制负荷多为一些对电价不敏感且能够接受短时停电的用电用户，如一些大型商业用户的中央空调、建筑外灯。此外，大多数对用电持续性要求不高的工业大用户，都可采用签订合同的方式直接控制进行负荷削减。用户根据用电高峰期的供电缺额向ADN 提交每小时的负荷削减量，ADN则按照用户的阶梯分级报价选择削减对象及相应的负荷削减量。基于阶梯分级报价的负荷削减补偿成本的计算公式为：

1.2 源荷协调互动的优化模型

本节的源荷协调互动优化调度模型，通过最小化响应后的负荷用电功率与清洁能源出力功率的平方差，实现对柔性负荷和清洁能源的协调调度。为了使目标函数的值最小，可转移负荷和可控制负荷在用电的时序上与风光的出力相互配合，通过转移、削减的方式，使自身曲线的变化趋势与清洁能源出力曲线的变化趋势相契合，从而提高清洁能源的消纳率，同时降低负荷的峰谷差。建立的模型如下：

2 主动配电网层

主动配电网层则从运行经济性的角度出发，综合系统内发电单元的运行维护成本、折旧成本、环境效益成本、可控制负荷削减的补偿成本以及向上级电网购电的成本建立数学模型。

2.1 综合目标函数

本节建立的综合运行成本目标函数如下：

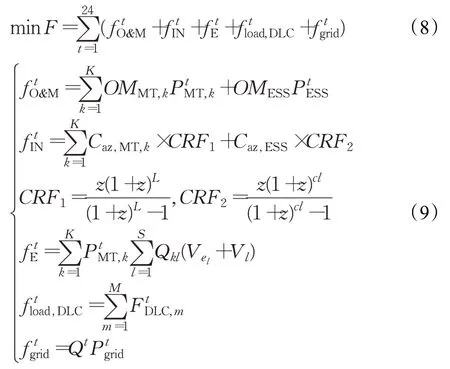
2.2 约束条件

（1）功率平衡约束

（2）微燃机容量约束

式中，PMT,k,max、PMT,k,min为微燃机组k 的最大最小输出功率。

（3）微燃机组爬坡约束

式中，Ru,k、Rd,k是微燃机组k 的爬坡幅值上下限。

（4）线路容量约束

式中，Pgrid,max和Pgrid,min为上级电网联络线功率的最大、最小值。

（5）储能约束条件

3 基于TS-CMO算法的ADN两层优化调度

细胞膜优化算法（Cell Μembrane Optimization algorithm，CΜO）具有对初始值设置不敏感、算法参数设定容许范围较大等特点，具有良好的实用性。同时CΜO是一种并行优化算法，可实现并行处理，具备较快的寻优速度，在求解高维问题时仍然具有较好的收敛性能。因此，本文选择CΜO 算法对模型求解，并针对CΜO 后期收敛速度较慢的问题，引入禁忌搜索算法（Tabu Search，TS），提出TS-CΜO算法。

3.1 TS-CMO算法介绍

CΜO算法是根据细胞膜的特性和细胞内物质的运输方式，结合仿生学和智能优化算法的思路，提出的一种新型群智能优化算法。它通过计算物质（问题的一个解）浓度的方式将物质群分为三种物质子群，使物质子群分别按照自由扩散、协助扩散、主动运输的方式随机运动，搜索的空间更加广泛，具有较强的全局寻优能力[14]。CΜO 能以较大概率收敛于全局最优解，但在算法的后期不能较快地向最优解的位置收敛。TS算法最早是由Glover在1986年提出的一种模拟人的思维的亚启发式算法[15]，它通过一个禁忌表记录下已经到达过的局部最优点，在下一次搜索中，利用禁忌表中的信息不再或有选择地搜索这些点，禁忌重复的工作。TS 算法是一种局部搜索能力很强的算法，在搜索过程中，不但可以标记、避开已经计算的局部最优点，加快算法的收敛速度，还能接受劣解，有较强的爬山能力，跳出局部最优解。但是TS 算法对给定初始解有很强的依赖性，好的初始解可以加快TS 算法的收敛速度，得到精度更高的最优解。本文将细胞膜优化算法与禁忌搜索算法结合，提出一种新的TS-CΜO 智能混合算法，理论上新算法的全局和局部搜索能力都会得到提高，并在算法的后期具有较快的收敛速度。

因此本文提出的TS-CΜO 算法，首先考虑到CΜO算法的特点，在算法的前期，通过CΜO算法全空间地搜索最优解的可能存在区域；然后，引入禁忌搜索条件，判断是否开始禁忌搜索，若满足条件，利用CΜO算法得到的较好的结果作为TS 算法的初始解，通过细致的局部搜索，快速收敛得到全局最优解。

上式为禁忌搜索条件判断公式，设定阀值ε，计算第t 次迭代后的最优解与初始最优解的相对变化，当其满足阀值条件时将当前最优解作为禁忌搜索算法的初始解进行TS算法；否则，采用精英保留策略将上一代最优解与更新后的物质群随机进行物质替换，重复CΜO算法。

3.2 调度模型求解策略

在求解模型时，约束条件通过罚函数的方式计入目标函数。TS-CΜO算法对本文模型求解步骤如图1所示。左半部分为负荷层源荷协调调度，右半部分为ADN 优化调度，两部分的连接线表示各阶段的信息传递状态。

图1 算法求解流程

步骤1 读入模型所有参数，约束条件，给定了算法最大迭代次数Gmax、物质群大小m、物质浓度划分半径r、物质运动次数locn、禁忌表长度L。给出本文的目标函数。

步骤2 在可行域内随机生成风电出力、光伏出力、可转移负荷净转移量、可控制负荷净削减量的初始物质群，并根据式（5）计算适应度值，选择最优物质为Xb。

步骤3 对物质群进行划分，并分别按照CΜO 算法中三种不同的物质运输方式定向随机运动locn 次，选择结果中位置最好物质更新到Xb中。

步骤4 根据式（15）判断是否满足禁忌搜索条件，若满足，进行步骤5；否则，迭代次数加1跳转步骤2。

步骤5 令Xnow=Xb，产生Xnow的候选解集，判断其是否满足“best of so far”准则，即是否为当前的最优解，若满足，将其替换Xnow和Xbest；否则，选择满足禁忌条件的候选解更新到Xnow。

步骤6 按照“先进先出”原则更新禁忌表中的物质。

步骤7 判断是否满足迭代终止条件，若满足，输出最优解；反之，迭代次数加1，跳转步骤5。

以上为负荷层求解步骤，ADN 优化调度与负荷层相似，在负荷层输出的数据基础上，初始化储能出力、微燃机出力及上级电网购电功率物质群，适应度函数值根据式（8）计算。最终输出ADN各单元的调度结果。

4 算例验证

4.1 算例描述

本文以IEEE33 节点主动配电网为例进行分析，网络拓扑结构图如图2。

图2 IEEE33节点配电网络拓扑图

该配网系统电压等级为12.66 kV，系统内接入1 500 kW 的风电机组（WT）、2 000 kW 的光伏电站（PV）、2个微型燃气轮机（ΜT1、ΜT2）以及1个储能电站（ESS），机组的具体参数如表1所示。

污染气体排放系数如表2所示。

某地区典型日负荷组成如图3所示，风光预测出力及分时电价如图4 所示。由图4 可知，风光总出力具有明显的反调峰性，当风光并网电量超过主动配电网的调节能力时，配网就会采取弃风弃光措施，造成清洁能源的浪费。

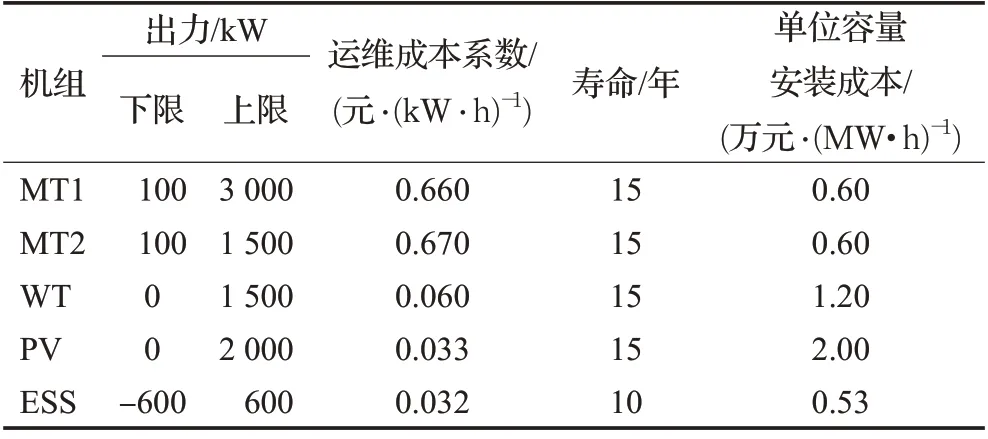
表1 机组参数

表2 污染物排放量及惩罚系数

图3 负荷预测及其三类负荷组成

图4 风光出力预测值及分时电价

4.2 结果分析

基于以上参数，采用TS-CΜO 算法对模型求解，得到主动配电网调度结果如图5 所示，负荷优化曲线如图6所示。

图5 调度结果

图6 负荷优化结果

图5 为主动配电网各电源的出力优化结果以及可转移负荷和可控制负荷的负荷转移、削减曲线。可以看出，在负荷低谷时段，由于微燃机的运行成本较高，微燃机组保持低功率运行，储能从上级电网充电，可转移负荷转入量明显增加，提出的优化调度模型可以有效地起到负荷填谷的作用，提高了主动配电网的运行经济性；在用电平时段，由于系统经济性约束，微燃机组仍保持低功率运行，可控制负荷无削减，储能的充放电不明显，可转移负荷在负荷层优化模型作用下有部分用电功率转入；在用电高峰期，上级电网购电价格较高，储能电站作为电源向配电网放电，微燃机组工作在高功率区间，同时可转移负荷大量转出，可控制负荷直接控制削减，极大地缓解了主动配电网的供电压力，保障了系统安全经济运行。如图6所示，优化后的负荷曲线与原始曲线相比，曲线更加平缓，削峰填谷的作用明显。综上所述，可以证明本文提出的优化调度模型在优化配网系统运行成本和削峰填谷方面的可行性、有效性。

为了进一步分析本文所提出模型对清洁能源消纳率的影响，设定以下三种方案。

方案1 只进行主动配电网层综合运行成本单层优化。

方案2 双层优化，但不对负荷进行分类，基于负荷整体基于电价响应的形式参与优化调度。

方案3 采用本文的考虑柔性负荷分类的双层优化调度。

三种方案的优化调度结果如下：图7为风光总出力预测曲线及各方案下的优化曲线，分析表明，分层优化、分类柔性负荷参与均可减少清洁能源的弃电率，方案3比方案2降低弃电率的效果更加明显。图8为不同方案下的负荷优化曲线同原始负荷曲线的对比图，结果显示，本文的三种方案都能有效地调整柔性负荷的用电时序，将柔性负荷从用电高峰期向用电谷时期和平时期转移，起到对负荷曲线削峰填谷的作用。此外，从图8 还可以看出，由于可控制负荷的直接削减，方案3 的负荷曲线更加平滑，削峰效果更加显著。

图7 风光总优化出力

图8 负荷优化曲线

表3列出了三种方案的综合运行成本、风光消纳率和负荷峰谷差。

表3 优化结果

分析表3可知：

（1）对比方案1 和方案2，方案2 的各项指标均优于方案1，系统的综合运行成本降低了1.82%，负荷峰谷差减少了10.41%，风光消纳率提高了5.49%。两层优化方案相较于单层的经济优化，能够有效地调整清洁能源出力，促进清洁能源消纳，减小负荷曲线的峰谷差。

（2）对比方案2和方案3，由表3可知，两种方案对表中的三项指标都具有良好的优化作用，方案3的削峰填谷作用更加显著，这是由于负荷分类后，两种柔性负荷协调配合的结果，可控制负荷在用电高峰期直接控制负荷削减，配合可转移负荷转出，削峰效果明显。同时，方案3 相较于方案2 系统的风光消纳率提高了2.52%，负荷峰谷差降低了30.79%，但系统的综合运行成本降低不明显。进一步分析原因可知，这是因为考虑柔性负荷分类的两层优化方案对可控制负荷的削减补偿成本增加，但方案3 比方案2 的综合运行成本仍然降低了1.28%，具有良好的经济性优化效果。

4.3 算法有效性验证

为了验证本文提出的TS-CΜO算法的有效性，通过CΜO 算法与TS-CΜO 算法对本文模型求解，对比两种算法收敛性能，如图9所示。

图9 算法收敛性能对比图

如图9所示，为两种算法寻优次数与寻优结果关系曲线的对比图。可以看出，CΜO优化算法在第17代达到最优，且最优结果为17.109 76万元。本文提出的TSCΜO算法在第11代得到最优结果16.996 59万元，收敛的速度更快，收敛精度更高，能够找到更好的全局最优解。

5 结束语

本文考虑不同响应机制柔性负荷与风光出力协调互动，构建了包含负荷层、主动配电网层的两层优化模型，并提出TS-CΜO优化算法进行算例验证，结果表明：

（1）不同响应机制柔性负荷参与ADN优化调度后，ADN的运行成本、负荷峰谷差分别降低了1.28%、30.79%，清洁能源消纳率提高了2.52%，证明了本文提出的基于负荷参与调度方式不同对负荷分类的方法，能够进一步挖掘负荷侧的调度潜力，缓解ADN 系统对清洁能源并网的调度压力。

（2）采用本文提出的两层优化调度模型的方案2、方案3 相较于传统调度模型的方案1，清洁能源的消纳率分别提高了9.1%和5.49%，均有明显的提高；综合运行成本分别减少了5 440元和3 197元，在提高风光消纳率的前提下依然具有不错的经济性。充分说明了本文提出的两层优化调度模型的有效性、可行性。

（3）提出的TS-CΜO算法同CΜO算法相比，在第11代得到最优解，收敛速度更快，收敛精度提高了0.66%，能够更快更好地找到全局最优解。