基于虚拟格网的建筑物点云轮廓线自动提取

徐景中，马丽娜

武汉大学 遥感信息工程学院，武汉430079

建筑物作为城市的重要组成部分，其轮廓线的自动提取对于点云测图、城市空间分析、建筑物三维建模等具有重要的应用价值。长期以来，建筑物轮廓线的提取一直是测绘、遥感学者的研究重点之一。

早期建筑物轮廓线的提取主要是基于遥感影像立体测图等方式进行，虽然获取结果精度较高，但工序复杂，周期长，成果的现势性难以保证[1-3]。而目前城市发展迅速，面貌日新月异，如何快速、自动地获取与更新城市建筑信息是目前亟需解决的问题。

具有三维数据采集能力的机载激光雷达（Light Detection And Range，LiDAR）技术的出现，为3D 建筑物轮廓线的快速获取提供了新的手段。对此，已有许多学者针对LiDAR 数据开展建筑物轮廓线的提取研究，如尤红建等[4]设计了一种基于LiDAR 距离影像的建筑物边缘自动提取方法。该方法在点云滤波的基础上，利用地面点与非地面点生成数字表面模型（Digital Surface Μodel，DSΜ）和数字高程模型（Digital Elevation Μodel，DEΜ）差值运算实现建筑物区域分割，然后利用拉普拉斯（Laplace）算子进行建筑物边界提取，并采用最小均方差逼近以及基于主方向的正交化完成建筑物轮廓线的提取。该方法展示了基于激光点云进行建筑物轮廓提取的可行性，但由于点云较为稀疏，提取结果跟实际建筑物形态差异较大。考虑到Laplace算子对噪声异常敏感，有学者针对建筑物点云生成的距离图像采用Canny等算子进行建筑物轮廓线的检测[5-6]，以改善轮廓线提取效果，但方法仍存在易受屋顶点云分布情况影响的问题，且结果存在人为内插误差。对此，部分学者尝试直接基于LiDAR点云进行建筑物轮廓线的提取研究。考虑到构建不规则三角网（Triangulated Irregular Network，TIN）是分析三维点云拓扑结构的常用方法，因此有部分学者基于TIN 方法开展建筑物轮廓线的提取研究。此类方法通常直接利用建筑物点云构建TIN，然后根据三角面元进行聚类或区域增长[7-8]，分割出屋顶同质区域，并利用TIN 边缘邻接关系分析提取建筑物轮廓线。考虑到轮廓线提取结果不规则，刘春等[9]进一步利用Dougls-Peucke算法进行轮廓特征点提取，并根据线段夹角对特征点进行分类，实现轮廓线的规则化处理。此类方法虽然能保留原始建筑物点云精度，但分析过程相对复杂，提取结果对阈值敏感。

为了避免TIN方法复杂的分析过程，蔡湛等[10]提出一种基于点云平面投影的建筑物轮廓提取方法。该方法搜索最大距离点作为起始边缘点，通过夹角判断实现边缘点的检测，在此基础上利用最小二乘分段拟合实现建筑物轮廓线的提取。该方法虽然无需点云构建TIN过程，但结果对阈值敏感。沈蔚等[11]针对建筑物点云采用Alpha-Shapes 方法进行轮廓线提取，并采用“袖子算法”以及矩形外接圆法进行轮廓线的规则化处理。该方法虽然无需构建TIN，但轮廓提取的精细程度依赖Alpha阈值，特别在处理凹型点集时，如果阈值过大凹拐角容易被钝化掉，如果阈值过小又容易得到破碎的点集形状。对此，李云帆等[12]提出双阈值方法以改善Alpha-Shapes方法的提取效果，虽然轮廓线提取结果的完整度有所提高，但阈值如何自适应设置仍是有待解决的问题。

此外，还有部分学者结合影像等数据源进行建筑物轮廓线的提取研究[13-14]，此类方法虽然可借助影像改善建筑物点云提取轮廓线的效果，但对轮廓线提取的数据源要求以及方法复杂度又提出了新的要求。

针对以上问题，考虑到数据的可获取性，本文提出了一种基于虚拟格网的建筑物点云轮廓线自动提取方法。该方法首先借助虚拟格网快速进行建筑物轮廓点的检测，并基于邻域分析与方向约束进行轮廓格网的追踪和优化，在此基础上，结合建筑物点云完成实际轮廓点的自动提取，最后采用基于随机抽样一致性（Random Sample Consensus，RANSAC）估计及最小二乘拟合方法实现轮廓线的自动提取。该方法无需建筑物单体化分割以及复杂的TIN分析过程，能直接从建筑物点云中提取轮廓线。

1 原理与方法

1.1 虚拟格网生成

由于激光点云空间分布离散，不利于建筑物轮廓线的检测处理，为了实现基于激光点云的轮廓线检测，通常需要构建点云邻域关系。本文针对建筑物点云，通过构建虚拟格网，以辅助点云的后续分析处理。虚拟格网的构建方法如下：

统计建筑物点云范围信息，并得到建筑物区域左下角坐标(xLD,yLD)；对于任意一点i 其所在的虚拟格网行列值(ci,ri)可通过下式计算得到：

其中，(xi,yi)为点i 的平面坐标(i=1,2,…,n);w 为虚拟格网尺寸，尺寸设置需要兼顾点云密度以及相邻建筑物间距，默认为平均点间距的2～3倍。

为了便于后续轮廓线提取，本文根据点云落入虚拟格网的数量进行虚拟格网的二值初始化处理，公式表示如下：

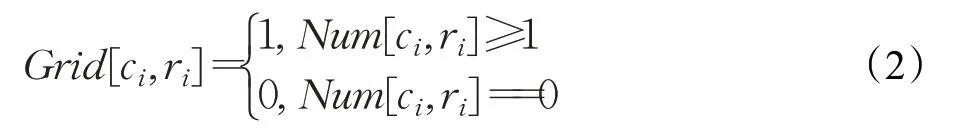
其中，Grid[ci,ri]为格网(ci,ri)的值，Num[ci,ri]表示格网(ci,ri)中建筑物点的数目。

1.2 边缘检测及追踪

1.2.1 边缘格网检测

考虑到建筑物轮廓点所在位置，其格网周围必存在无点云落入的邻域格网，因此本文基于虚拟格网通过分析其8 邻域格网值，进行边缘格网的快速检测。如图1所示，对于当前格网G 及其8 邻域，若8 邻域中存在格网值为0的情况，则标记当前格网为候选边缘格网。

图1 格网8邻域位置表示

1.2.2 边缘格网追踪

经过边界格网检测得到的仍是分布独立的边界格网，需要进一步追踪处理方可形成顺序连接的轮廓线。追踪过程仍采用8邻域分析方法进行处理，即基于上述过程检测的候选边缘格网，从任意一边缘格网出发，根据其8邻域的边缘格网分布情况，进行边缘格网的判断追踪，得到格网轮廓线。具体过程如下：

（1）搜索虚拟格网，若某格网为候选边缘格网，则将其加入堆栈，并标记该格网为当前边缘格网。

（2）以当前格网为中心，寻找其8邻域格网，并判断是否存在边缘格网。

（3）若8邻域存在边缘格网，则将其加入堆栈，并标记该格网为当前格网，重复步骤（2）。

（4）若当前格网的8 邻域不存在边缘格网，则重复步骤（1），直至所有格网均被标记，则停止追踪。

1.3 优化处理

考虑到直接基于边缘格网进行轮廓线追踪，会出现轮廓回路以及连接错误等情形，如图2 所示，因此需要进行边缘优化处理。

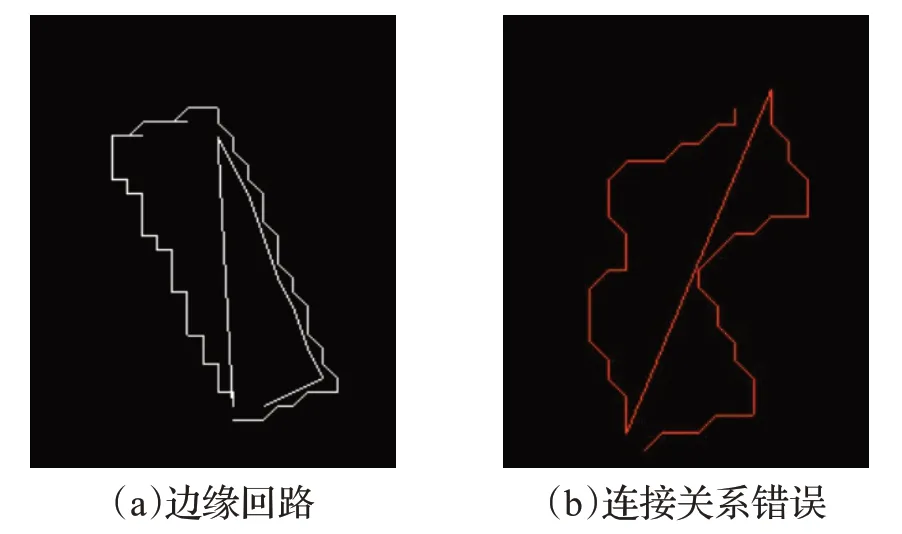
图2 边缘格网连接问题示意图

1.3.1 单边缘格网抑制

边缘回路通常是由于边缘位置存在多个候选边缘格网引起，考虑到同一方向上，若已存在轮廓边缘，那么在一个格网的邻域范围内不应存在同向的另一条轮廓边缘。据此，本文根据虚拟格网的邻域关系特征，设计了基于方向的单边缘格网抑制方法，以克服边缘线追踪回路问题。

如图3所示，若当前格网g[i,j]为边缘格网，则根据下一边缘格网与当前格网连接方向进行单边缘格网判断处理，处理过程如下：

（1）水平方向：若下一连接格网为g[i,j+1]，则继续判断其延伸方向的格网g[i-1,j+2],g[i,j+2],g[i+1,j+2]是否为边缘格网，若其中边缘格网数大于1，则进行边缘格网抑制处理，即保持距离该轮廓中心最远的格网为边缘格网，并将其他边缘格网设置为非边缘格网，否则不作处理；若下一连接格网为g[i,j-1]，则继续判断其延伸方向的格网g[i-1,j-2],g[i,j-2],g[i+1,j-2]是否为边缘格网，若其中边缘格网数大于1，则采用类似方法对其相邻格网进行抑制处理。

（2）垂直方向：若下一连接格网为g[i-1,j]，则继续判断其延伸方向的格网g[i-2,j-1],g[i-2,j],g[i-2,j+1]是否为边缘格网，若其中边缘格网数大于1，则进行边缘格网抑制处理，即保持距离该轮廓中心最远的格网为边缘格网，并将其他边缘格网设置为非边缘格网，否则不作处理；若下一连接格网为g[i+1,j]，则继续判断其延伸方向的格网g[i+2,j-1],g[i+2,j],g[i+2,j+1]是否为边缘格网，若其中边缘格网数大于1，则采用类似方法对其相邻格网进行抑制处理。

（3）45°方向：若下一连接格网为g[i-1,j+1] ，则继续判断其延伸方向的格网g[i-2,j+1],g[i-2,j+2],g[i-1,j+2]是否为边缘格网，若其中边缘格网数大于1，则进行边缘格网抑制处理，即保持距离该轮廓中心最远的格网为边缘格网，并将其他边缘格网设置为非边缘格网，否则不作处理；若下一连接格网为g[i+1,j-1]，则继续判断其延伸方向的格网g[i+1,j-2],g[i+2,j-2],g[i+2,j-1]是否为边缘格网，若其中边缘格网数大于1，则采用类似方法对其相邻格网进行抑制处理。

（4）135°方向：若下一连接格网为g[i-1,j-1]，则继续判断其延伸方向的格网g[i-2,j-1],g[i-2,j-2],g[i-1,j-2]是否为边缘格网，若其中边缘格网数大于1，则进行边缘格网抑制处理，即保持距离该轮廓中心最远的格网为边缘格网，并将其他边缘格网设置为非边缘格网，否则不作处理；若下一连接格网为g[i+1,j+1]，则继续判断其延伸方向的格网g[i+1,j+2],g[i+2,j+2],g[i+2,j+1]是否为边缘格网，若其中边缘格网数大于1，则采用类似方法对其相邻格网进行抑制处理。

图3 单边缘格网抑制方向示意图

1.3.2 连接关系调整

连接关系错误主要是由于8邻域迭代追踪时，格网沿某一方向追踪完成后重新回到起点继续追踪导致的连接顺序颠倒引起的。考虑到连续的轮廓线，对应的轮廓格网也是顺序连接的，不应存在距离突变，因此可设计距离判断方法进行连接关系分析与调整处理。具体处理过程如下：

（1）以任一边缘为当前边缘，从起点出发顺序计算该边缘相邻节点之间的距离，若间距大于阈值（设为2w），则表明该边缘存在连接关系问题，将该边缘在此处断开。

（2）继续判断后续线段的节点间距是否满足阈值条件，若大于阈值则继续断开，直至抵达该边缘的终点。

（3）针对边缘断开的各线段，从任一线段端点出发，搜索离其最近的其他线段端点，若端点之间的距离小于阈值，则将该线段与当前线段连接，继续判断新加入线段的端点的连接情况；否则保持断开处理。

（4）继续判断其他线段端点连接情况，直至所有线段完成判断，则当前边缘的连接关系调整处理结束。

（5）重复步骤（1）～（4），直到所有边缘完成调整，结束处理。

1.4 实际轮廓点提取

考虑到直接基于虚拟格网方法提取的建筑物轮廓线，其位置和精度会受到格网尺寸的影响，因此本文基于虚拟格网的提取结果，进一步结合原始建筑物点云进行实际建筑物轮廓点的提取。具体方法为：

（1）遍历所有建筑物的格网轮廓线追踪结果，并计算轮廓多边形的中心点坐标。

（2）从任一格网轮廓点出发，根据其中边缘点分布以及轮廓边缘连接方向进行实际轮廓点的检测。

①若当前格网中只有一个点，则直接以该点位置作为实际轮廓点位置；

②若当前格网中存在多余一个点，则根据轮廓多边形中心点与当前格网中心连线方向，以及当前边缘线线段连接方向，判断实际轮廓点所在的格网区域，并以距离多边形中心点最远的点作为实际轮廓点；

③以虚拟格网边缘的连接顺序，依次连接实际轮廓点，得到建筑物的实际轮廓线。

1.5 轮廓线规则化

经过以上处理得到建筑物轮廓线通常呈现”锯齿”状，一般需要进行规则化处理。虽然Douglas Peucker算法是一种常用的矢量线压缩经典算法，但该算法易受噪声点影响，对于点云提取的轮廓线常出现变形。考虑到随机抽样一致性（RANSAC）方法对噪声具有更好的鲁棒性[15]，最小二乘方法具有最好的拟合精度[16]，本文拟结合二者优点，通过RANSAC估计初始的直线位置，得到属于直线的点，并利用这些点进行最小二乘拟合得到直线方程，以保证轮廓简化的结果保持原始轮廓的形状。具体步骤如下：

（1）线段拆分步骤：从任一条轮廓线出发，顺序选择三点，并采用RANSAC 直线模型估计方法得到一条直线；如果三点到该直线距离均小于阈值th_dist（设为w），则表明三点位置存在一条有效直线，并将三点加入点链表中，继续判断后续点到该直线的距离，若有新的点加入链表，则重新进行直线估计；否则，新建点链表，采用同样的方法进行轮廓点的拆分判别，直到所有点判别完毕，则完成线段拆分处理。

（2）利用拆分得到的点链表，采用最小二乘直线拟合方法依次拟合直线。

（3）以最长线段方向作为建筑物主方向，其他线段若与主方向夹角近似平行或垂直（th_angle），则进行线段的斜率调整。

（4）针对每条直线段，根据轮廓点与原始轮廓中心连线与直线相交情况判断是否进行直线外扩处理；若存在相交情况，则利用原始轮廓点重新计算直线参数。

（5）依次进行直线两两相交处理，得到新的轮廓点；相交处理时，顺序连接这些点，即可完成建筑物轮廓线的提取。

2 实验与分析

为了验证本文方法的有效性，采用Visual C++实现上述方法，计算机操作系统为Windows 10，CPU 为i7-6600，内存8 GB。实验数据来自Gipuzkoa 城市的机载激光点云，区域范围为1 000 m×808 m，点云平均密度为1.3 点/m2。点云渲染效果如图4 所示。从图中可以看出，该区域点云已经过分类处理，其中建筑物分布密集，且大小不同，形状各异。

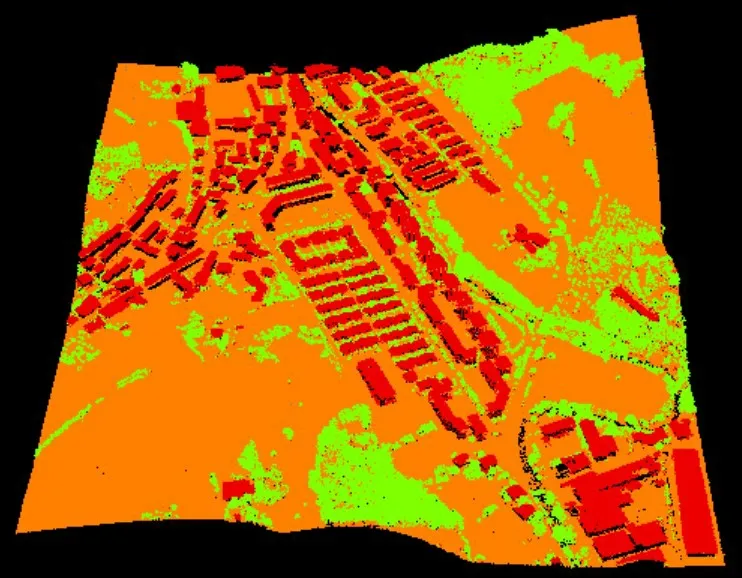
图4 测区点云按类别渲染效果

针对建筑物点云，采用虚拟格网方法进行建筑物轮廓点的检测(w=2 m)，图5为建筑物轮廓点与建筑物点云叠加显示效果。从图中可以看出，所有建筑物的候选轮廓点均被检测出来，能与建筑物点云很好地吻合，但这些点是基于虚拟格网直接检测的结果，因此存在一些位于轮廓附近的伪边缘点，需要进行真实轮廓点的提取。

图5 建筑物边缘点检测结果

图6为建筑物轮廓线检测结果，其中轮廓线优化前后局部对比如图（a）与图（b）所示。从图中可以看出，在进行轮廓线优化处理前，较多轮廓线存在追踪回路以及连接顺序错误等问题，经过轮廓线优化处理，轮廓线连接关系正确。

图7为轮廓线提取结果与建筑物点云叠加效果图，其中图（a）为直接基于虚拟格网中心位置输出的轮廓线，图（b）为由真实轮廓点形成的轮廓线。从图中可以看出，直接基于虚拟格网中心得到的轮廓线虽然接近建筑物轮廓位置，但并不能与建筑物轮廓点较好地吻合，二者存在一定的偏差，而图（b）由真实轮廓点构成的轮廓线，点位正确，能较好地包含建筑物点云。

表1 轮廓线相对误差统计表

图6 边缘线优化结果局部对比

图7 轮廓线与点云叠加效果对比

为了验证本文方法对建筑物轮廓的保持效果，本文在对建筑物点云单体化分割的基础上，采用Alpha-Shapes方法进行建筑物轮廓线的提取，并以此为参考将本文提取结果与Alpha-Shapes 方法提取结果进行叠加对比，如图8（a）所示。图8（b）为采用文献[5]方法提取结果与Alpha-Shapes结果叠加效果。从图中可以看出，虚拟格网提取方法与Alpha-Shapes 方法提取结果基本重叠，在细节上存在一些区别，而文献[5]方法由于存在内插误差，结果与Alpha-Shapes方法结果存在整体偏移。

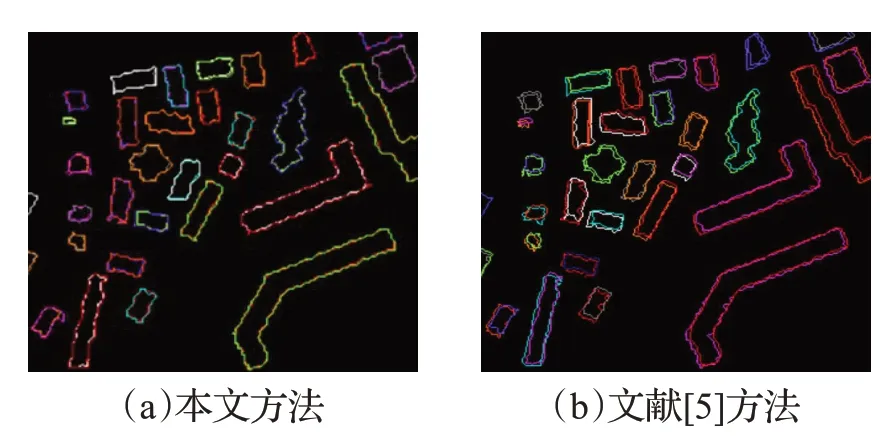
图8 轮廓线提取结果与Alpha-Shapes方法结果叠加对比

为了定量分析两者偏差，本文分别计算建筑物轮廓多边形中心点位置以及面积，并以Alpha-Shapes方法提取结果作为参考值，进一步分析提取结果中心位置以及面积误差，具体公式如下：

（1）均方根误差（Root Μean Square Error，RΜSE），提取的轮廓中心点坐标与参考中心坐标差值的平方和与点数比值的平方根。RMSE 越接近0说明中心点越接近参考位置。

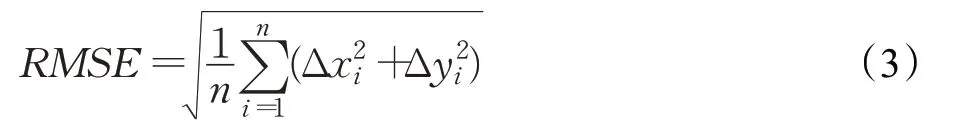
式中，n 为多边形中心点个数。

（2）面积相对误差（Relative Area Error，RAE），提取的轮廓多边形面积与参考面积之差与参考面积的比值。REA 越小，说明提取的轮廓面积更接近参考面积，算法效果越好。

式中，ΔAi为提取面积与参考面积之差，A 为参考面积。

建筑物轮廓线提取结果的相对误差如表1 所示。从表1 可以看出，本文方法提取结果与Alpha-Shapes 方法结果相比，其多边形中心点位RΜSE为0.512 m，约为虚拟格网尺寸的1/4，而平均RAE 为6.7%，说明两者位置接近且形状细节具有较高的相似性。文献[5]方法提取结果与Alpha-Shapes方法结果误差相对偏大，中心点位最小轴向偏移达0.022 m，RΜSE 为0.882 m，平均RAE为11.8%，说明二者存在整体偏差。

表2 为不同方法进行轮廓线提取的耗时统计表。考虑到阈值不同耗时有所差异，本文测试了3 组阈值下各种方法的耗时情况，分别为1 m、2 m、3 m。对于Alpha-Shapes方法，阈值对应该方法的Alpha阈值，而对于本文方法以及文献[5]方法则分别对应虚拟格网尺寸以及图像分辨率，其中Alpha-Shapes 方法所需时间未包含建筑物点云单体化分割时间。从表中可以看出，Alpha-Shapes方法比较耗时，所需时间远大于后两种方法，且随着阈值增大，该方法所需时间快速上升；文献[5]方法耗时最短，响应最快；本文方法在不同阈值条件下的耗时均与文献[5]方法接近，且呈下降趋势。

表2 不同方法轮廓线提取耗时统计表

为了进一步测试本文方法在不同阈值条件下的耗时成本，本文统计了不同阈值下的时间成本，耗时成本趋势图如图9所示。

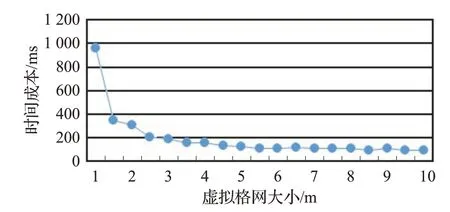
图9 耗时成本趋势图

从图9 中可以看出，随着阈值的增大，时间成本逐渐下降，并在4 m 以后逐渐趋向平稳，耗时成本维持在100 ms附近波动。

图10 为建筑物轮廓线规则化效果（th_angle=15°），从图中可以看出，建筑物轮廓线完整，形状规则，与建筑物点云相比（图5），形状被较好地保持。

图10 建筑物轮廓线规则化结果

3 结束语

建筑物轮廓线的自动提取是基于激光点云进行制图及建模的关键步骤，本文提出一种基于虚拟格网的建筑物点云轮廓线提取方法。该方法借助虚拟格网实现建筑物轮廓格网的快速检测，可避免建筑物点云单体化分割处理过程，同时可以保持原始建筑物轮廓点精度及完整性；追踪过程基于方向的单边缘抑制处理以及连接关系调整，可有效保证轮廓提取结果的正确性；在轮廓线规则化处理中，采用基于RANSAC 估计的轮廓线分段及规则化处理，以保证轮廓线提取结果不变形。进行实地点云验证，结果表明本文方法可快速实现建筑物轮廓线自动提取，且提取结果与Alpha-Shapes方法结果位置与形状均相近，可为建筑物轮廓线的自动提取提供一种可行的解决方案。