动态环境下多重A*算法的机器人路径规划方法

华 洪，张志安，施振稳，陈冠星

南京理工大学 机械工程学院，南京210094

路径规划技术是移动机器人技术的核心内容之一，近年来在许多领域都有着广泛的应用，例如在制造领域中应用于生产线上下料搬运的自主引导运输车，在电商工厂中应用广泛的无人送货小车，在家中负责清扫地板的扫地机器人等。它们都是在不同的环境下，按照指定要求，以感知、建模、规划、执行的标准路径规划方法执行[1-2]。根据路径规划环境是否已知，可将路径规划算法分为全局路径规划与局部路径规划。根据路径规划环境中是否存在动态障碍物，可将路径规划分为静态路径规划与动态路径规划[3-4]。

A*算法作为一种全局的静态路径规划搜索算法，具有鲁棒性好、反应快等优点，但受算法原理限制，规划出来的路径折线较多，且随着环境变大搜索代价呈指数增长。文献[5]提出对A*算法中的估价函数进行指数加权处理，并且对路径进行5 次多项式平滑处理，有效解决了搜索效率低和路径不平滑的问题，但机器人并不具备局部规划能力与动态避障能力，在密集区域内容易陷入极小值。文献[6]提出在A*全局规划的基础上，采用自适应步长调节方法的人工势场法进行局部路径优化，且在局部路径规划的同时增设虚拟目标点，让机器人能够逃离陷进点，但机器人并不具备动态避障能力，且规划出来的路径可能非最优。文献[7]针对机器人在类似超市环境等密集区域下的路径规划问题，在A*算法基础上提出了一种动态环境下机器人多状态自主导航方法，在狭窄通道与动态障碍物的环境下，机器人都有良好的避障策略与局部规划能力，但其考虑参数过多，容易导致全局路径非最优。

针对以上方法的特点与不足，本文提出一种基于A*算法的改进的路径规划方法。首先在传统的全局A*算法之上将路径节点进行优化，按照删除冗余点准则与新增节点准则，减小全局规划任务，提高效率；再结合滚动窗口法的思想，在既定的滚动周期内，结合全局规划的节点信息，按照一定准则在局部环境中生成子目标；在该环境内加入动态避障控制策略的同时再进行“全局路径规划”，根据传感器探测范围，如果环境范围过大再生成子局部环境，依次递归，进行多重A*算法，直至机器人能够到达子目标点。在Μatlab 软件中建立栅格图进行仿真，仿真结果表明，相比于传统的A*算法，改进算法下机器人能在部分地图信息未知的情况下实现局部路径规划，并拥有良好的避障功能，且消耗的时间更少，路径的长度更短。

1 改进A*算法

A*算法是在Dijkstra 和BFS 两种算法的基础上提出的静态网络最优路径搜索方法，它是一种启发式的搜索算法[8]。传统A*算法仅适用于全局的静态环境，同时由于启发式搜索的原理限制，并不会考虑到路径节点连线的平滑度。针对传统A*算法的局限性与不足，进行以下改进：

（1）优化路径节点，平滑路径轨迹；

（2）结合滚动窗口法，综合节点信息确定局部路径规划区域；

（3）加入避障控制策略，在局部路径规划过程中保证机器人在较短时间内到达子目标点。

1.1 优化全局路径节点

传统A*算法是以最短路线优化目标，规划出来的全局路径在复杂的环境下通常会出现折线较多的情况，原因是其包含部分冗余点以及一些不必要的转折点，易导致机器人运动的角速度及向心加速度发生变化，现采取以下方法准则对路径节点进行优化：

删除节点准则：若当前点与其父节点、下一节点在同一直线上，则判定该节点为可删除节点；若当前点与其父节点、下一节点连线所成角大于α 小于180°，且父节点和下一节点的连线与不可通行区域无交点，则判定该节点为可删除节点。找出可删除节点剔除后，重新遍历新节点，更新路径。

新增节点准则：若当前节点和轨迹所成夹角与下一节点和轨迹所成夹角差值大于β，在两节点中点处新增一个节点，并将该节点沿轨迹法线方向以减小β 角的方向平移γ 个栅格单位，重新遍历新节点，确认路径与不可通行区域无交点后，更新路径。

1.2 局部路径规划

局部路径规划中移动机器人需要知晓环境信息与自身位置信息，利用外界传感器构造滚动窗口探测环境信息。本文结合滚动窗口法与A*算法进行局部路径规划的思想为：在构造的栅格地图环境中，设定起始点S、目标点E、传感器环境探测距离R、滚动窗口Vision，在规划完全局路径后，结合节点信息与窗口范围，选取若干局部路径规划区域与子目标点，在当前窗口内基于原规划路径实时进行局部路径规划，到达子目标点后更新局部路径区域，重复以上过程，直到最后一个滚动窗口刷新，到达目标点E，完成路径规划。

下面在构造的栅格地图环境中，对某个局部路径规划窗口进行数学建模。设栅格地图的环境大小为m×n，栅格尺寸为δ，工作空间为栅格集合J ，机器人当前位置栅格为sEn，目标栅格为sEn+1，机器人传感器探测距离R 视作矩形距离RV，如式（1）所示；滚动窗口Jn 为以栅格sEn中心点为圆心，RV为半径的圆形区域，d 为欧几里德距离，滚动窗口Vision 为滚动窗口Jn内栅格x 的集合，如式（2）所示。

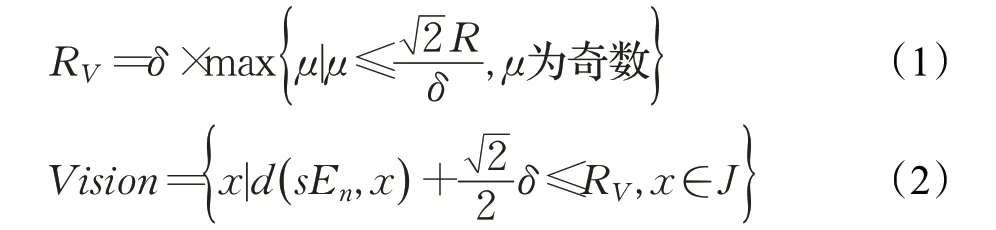
由式（1）可知，本文研究的移动机器人的探测栅格的规模t=RV/δ ，机器人的有效视野窗口Vision 的矩阵模型如下所示：

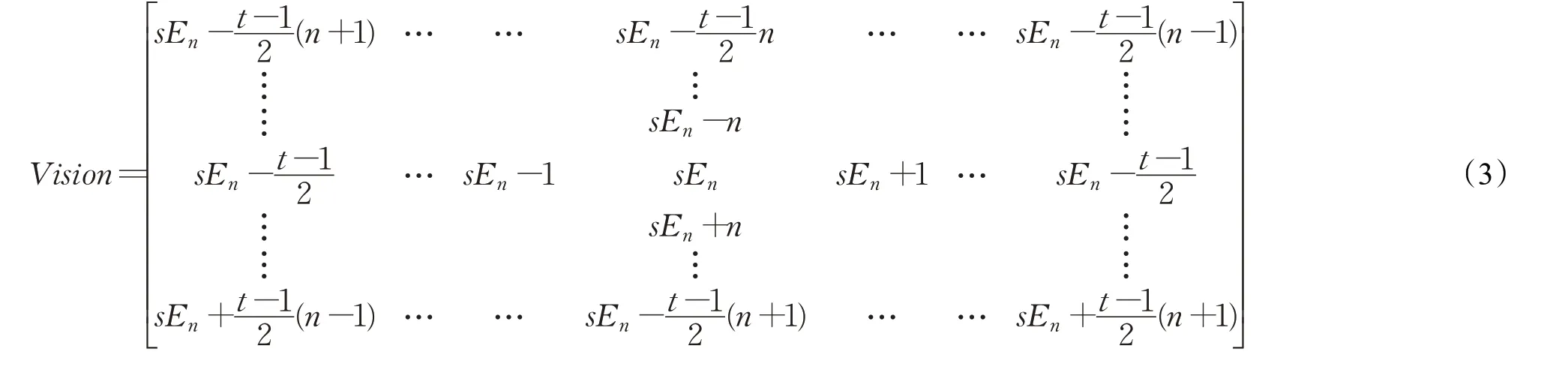
如图1所示，机器人处在一个10×10的栅格环境中，设定栅格尺寸δ=1,RV=3，当前机器人处于sEn点，也是坐标为（2，1）的栅格的中心，可计算得t=3,m=n=10。由式（2）和式（3）可推得机器人在该环境下的有效滚动窗口视野栅格包括：Vision={(1,1);(2,1);(3,1);(4,1);(1,2);(2,2);(3,2);(4,2);(1,3);(2,3);(3,3)}。

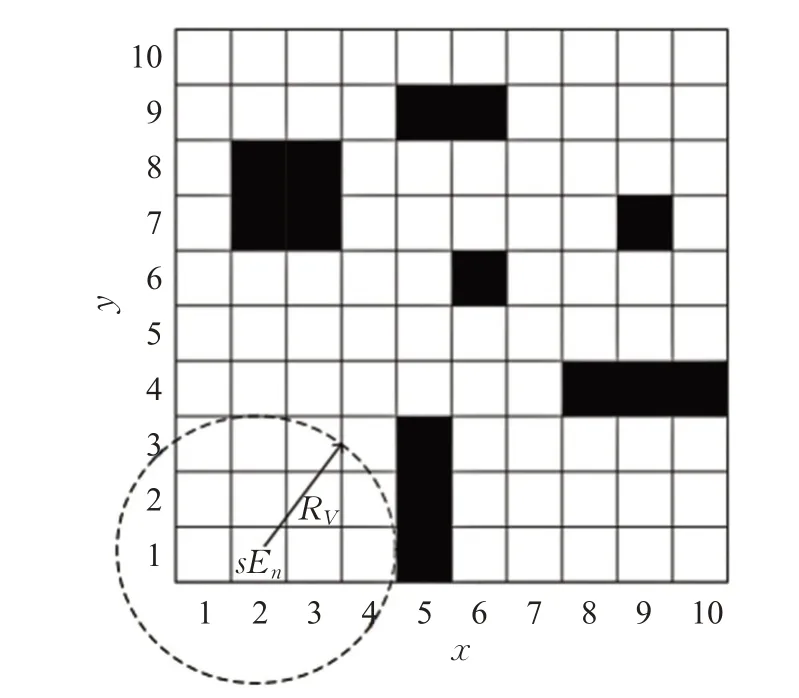
图1 滚动窗口环境下的栅格环境模型

假设整个路径规划过程完成了n 次局部路径规划，第m 次局部路径规划的路径为D(m)，则全程的路径可以表示为：

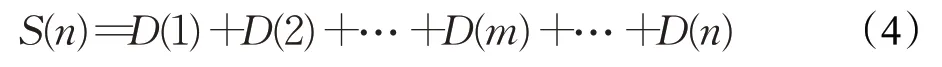
由式（4）可知，局部子目标点sE 的选取对于路径通往终点E 具有导向作用，需要建立起始点、局部子目标点sE 与终点E 的联系。因此，局部路径规划过程的关键点在于局部子目标点的选取。结合全局路径节点，本文提出将局部子目标点所处位置分为多种情况讨论。

（1）局部子目标点与节点重合但处于可行域内

若当前环境过小，将会出现目标点E 在第一个滚动窗口中的情况，此时目标点E 与局部子目标点重合，这种情况即为全局路径规划。若目标点E 并未出现在第一个滚动窗口中，则从起点开始，选取在每个滚动窗口中出现的序列号最大的节点作为第一个子目标点。

（2）局部子目标点与节点不重合但处于可行域内

若在某个滚动窗口中，因环境过大或在优化全局路径时删除的序列点过多，导致序列点过于稀疏，传感器检测不到下一节点信息，此时新增的局部子目标点设定于机器人滚动窗口范围Vision 与原规划路径的交点处。

（3）局部子目标点处于不可行区域内

若在某个滚动窗口中，检测到在全局路径规划之前并未记录到的障碍物，且障碍物恰好与本应设定的局部子目标点重合，这种情况出现时需要加入新的障碍物信息，更新地图，重新进行全局路径规划，直至本次滚动窗口的局部子目标点设定在可行域内。

下面给出局部子目标选取的数学模型：

滚动窗口Vision 的栅格集合可由式（2）和（3）推得：

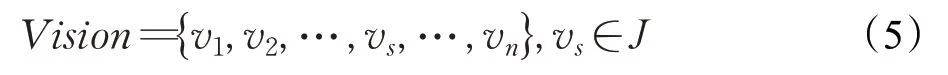
其中，s ∈{1,2,…,n},Vision包含栅格总数为t2=(RV/δ)2。

由式（5）可以推出滚动窗口视野中栅格点的坐标集合为：

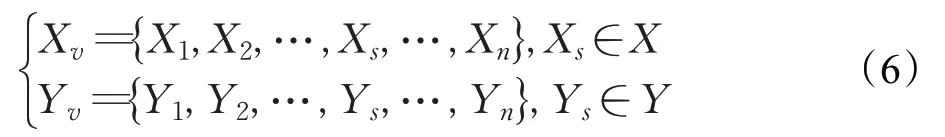
式中，X、Y 为栅格环境中所有栅格点的横纵坐标值所组成的集合。

滚动窗口中任意栅格点到目标点的距离函数为：

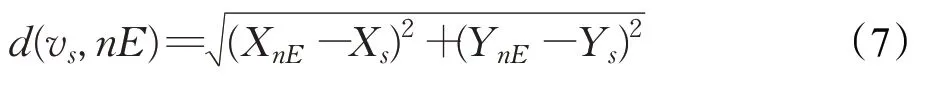
为了研究方便，移动机器人在栅格环境中的移动方向可看成是前、后、左、右、左前、右前、左后、右后8个方向，即从当前栅格向邻近栅格行径有8 个方向，不妨设左前方是不可通行点，则机器人可运动方向共有7 个，可表示为：

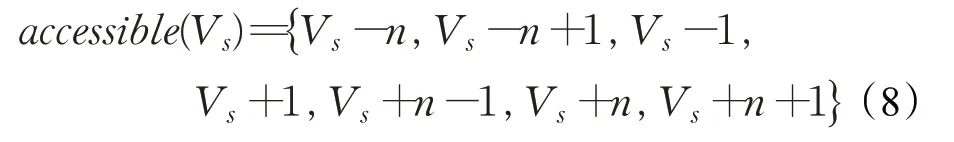
当前点栅格到相邻栅格的距离可表示为：

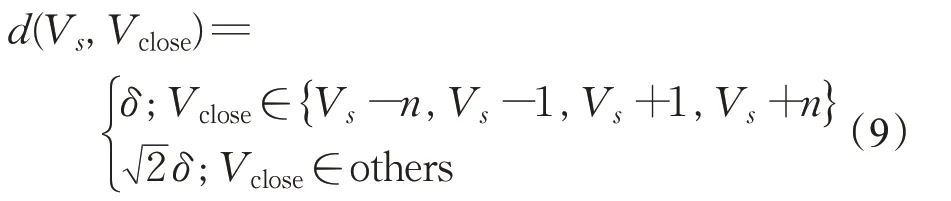
由式（5）～（9）可推得，局部子目标sE 选取规则的数学模型为：

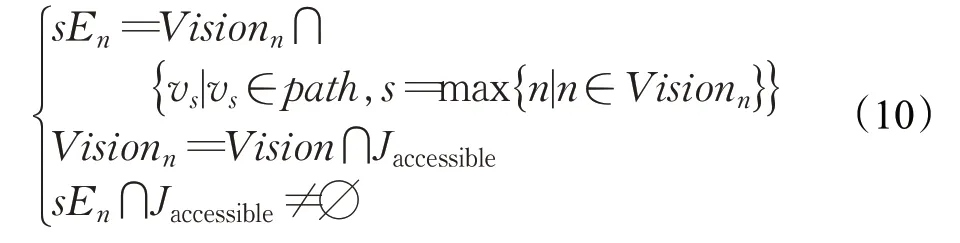
1.3 避障控制策略

移动机器人如何在未知环境下自主躲避动态障碍物一直是路径规划问题的难点。本文为了研究方便，将动态障碍物的运动做匀速直线运动处理，同时对于障碍物的体积和形状做点化处理，即不考虑障碍物的具体尺寸和大小。

自主移动机器人避障技术发展以来，可将其避障控制结构分为两大类：反应型控制结构和慎思型控制结构[9-10]。反应型控制结构是指机器人的感应器在接收到障碍物信息后，执行器直接执行设定好的指令，即“感知-执行”的过程，这种控制结构优点是反应迅速，缺点是缺少全局观。如文献[11]与文献[12]中采用的避障策略，在复杂环境下容易无法到达最优点。慎思型控制结构为“感知-规划-执行”，这种控制结构的机器人一定要具备分布式的嵌入式控制结构，感应器的信息首先传入上层决策层，经过决策层分析处理后才传入执行机构做出动作，这种控制结构的智能化程度虽然提升了，但是控制结构过于臃肿，往往在设备性能不高的情况下难以实现。如文献[13]与文献[14]就是这种控制结构，它将避障环境分为两种情形，每种情形下障碍物不同的运动方向避障策略也截然不同，这在真实环境下是难以实现的。

结合前文中的路径规划方法，本文综合反应型控制结构和慎思型控制结构的优点，在局部路径规划过程中，基于云的协作定位系统，使用卷积层和ConvLSTΜ层的组合算法确定动态障碍物与局部路径轨迹的关系[15]，混合使用上述两种避障控制结构。

（1）动态障碍物轨迹与路径轨迹重合，如图2和图3所示。

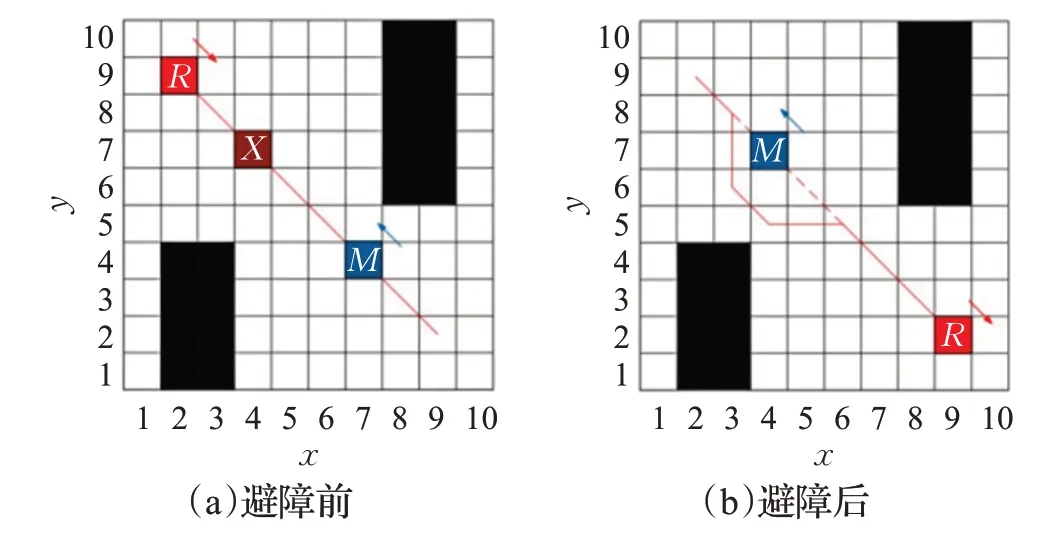
图2 障碍物轨迹与路径方向相反

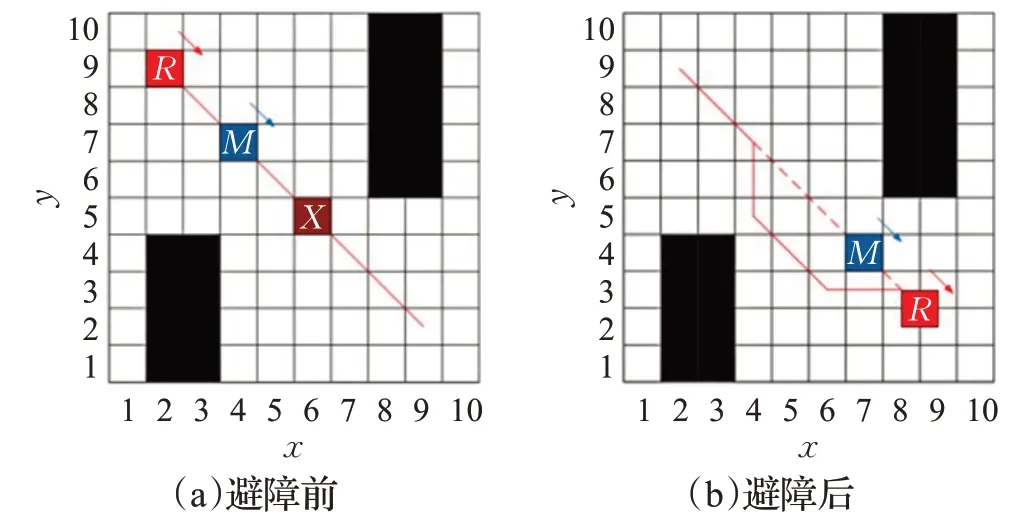
图3 障碍物轨迹与路径方向相同

图中红线表示机器人原定的路径轨迹，红色方块(R)表示移动机器人，蓝色方块(M)表示膨化处理后的障碍物，褐色物块(X) 表示膨化处理后的碰撞位置。图2表示障碍物的行进方向与机器人的行进方向相反，此时采用反应型控制策略，机器人向路径法线方向平移一个栅格单位的距离，在与障碍物距离开始递增并且大于一定阈值时，机器人返回原轨迹行驶。图3表示障碍物的行进方向与机器人的行进方向相同，当障碍物的速度大于机器人的行驶速度，易知机器人可按原轨迹行进，当障碍物速度小于机器人的行驶速度，机器人采用慎思型控制结构，计算出碰撞点位置后，将碰撞点膨化处理为不可行点，重新进行路径规划，更新路径。

（2）动态障碍物与路径交为一个点或多个点，如图4和图5所示。

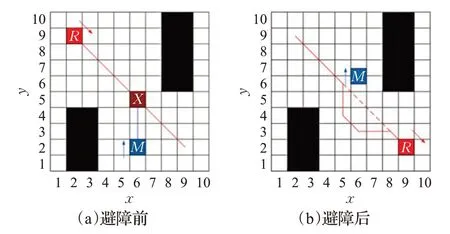
图4 障碍物速度小于机器人行进速度

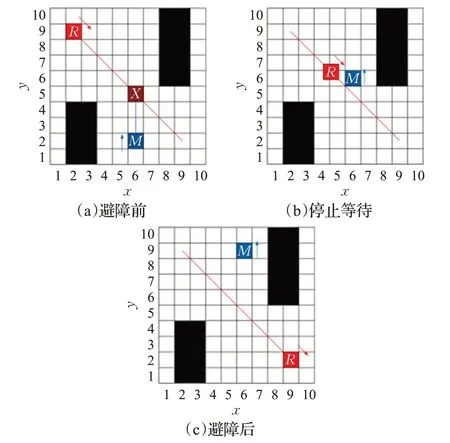
图5 障碍物速度大于机器人行进速度

当动态障碍物行径与路径轨迹的交点非碰撞点时，易知机器人可按原路径行驶，不予讨论。当障碍物的行径与机器人有一个碰撞点时，若动态障碍物速度远小于机器人行进速度，采用慎思型控制结构，如图4所示，可按照障碍物的速度大小将碰撞点做相应的膨化处理，将膨化区域视作不可行区域，重新进行局部路径规划，更新路径。若障碍物速度远大于机器人速度，将导致膨化区域过大，应采用反应型控制策略，如图5所示，机器人在碰撞点前等待，待障碍物穿过机器人规划路径后，再按原路径行驶。

2 实现流程

2.1 地图及算法环境处理

为了便于研究，本文对移动机器人及环境地图做以下设定：

（1）采用栅格法对环境地图进行数学建模，可行进区域与不可行进区域分别用白色栅格与黑色栅格表示。

（2）地图环境的起点、终点已知，地图中部分障碍物信息未知。

（3）将移动机器人与动态障碍物点化后膨化处理。

（4）地图环境中的动态障碍物做匀速直线运动，但障碍物速度方向、出现规律未知。

（5）移动机器人带有传感器，能够感知有限范围内地图的信息，如障碍物的方位、速度等。

（6）移动机器人的运动为匀速运动，且可全向运动。

2.2 算法流程

动态环境下的多重A*算法流程如下：

步骤1 算法的初始化。初始化系统参数：路径规划的起始位置S，目标位置E，栅格尺寸δ，栅格数量n，生成工作空间栅格集合J ；初始化算法参数：机器人传感器探测距离R，路径优化参数α、β、γ。

步骤2 基于已知的环境信息，生成全局路径并优化全局路径。以传统算法生成路径后，经删除节点、新增节点优化路径，生成可参照节点信息，基于该部分的节点信息进行初步局部路径规划。

步骤3 选取当前环境下滚动窗口的子目标点，判断当前子目标点信息，若当前子目标点处恰好为不可通行栅格，则转到步骤2，若子目标点处为可通行栅格区域，则转到步骤4。

步骤4 在当前局部路径规划区域内采用起始点为sEn、目标点为sEn+1 的多重A*算法，同时引入避障策略，根据动态障碍物信息的不同，混合使用反应型控制结构和慎思型控制结构。

步骤5 在到达局部子目标点后，判断当前位置是否与目标终点E 重合，若不重合，则跳到步骤3；若重合，说明机器人已到达目标位置，算法结束。

3 仿真分析

3.1 多重A*算法与原算法的比较

为了验证多重A*算法有较好的全局路径规划能力与局部路径规划能力，本文在不同环境下将多重A*算法与A*算法进行实验仿真比较。实验在CPU为I7-8700，RAΜ 为16 GB 的计算机上运行，算法通过Μatlab 编程仿真实现。

3.1.1 路径轨迹的比较

本文算法相比于传统A*算法，在静态全局路径规划问题上主要是对规划的路径轨迹进行优化处理。在20×20 的栅格环境下，以（1，1）为起点，（20，20）为终点进行传统A*算法的全局路径规划后，用本文算法优化路径节点。

优化路径节点的关键在于参数α、β、γ 的选取，α、β 越小理论上优化效果越好，但α 过小容易导致节点少，路径不平滑，β 过小规划轨迹容易与不可行域相交，同时α、β、γ 的选取也与环境大小、障碍物覆盖率相关。在20×20 的栅格环境下，经过多组数据仿真比较，选取参数α=126°,β=58°,γ=2 下路径的优化效果最好，优化轨迹的参考标准有累积转角、平均转角、路径长度。图6为路径节点的优化过程，红线表示生成的全局路径。图6（a）为传统A*算法生成的路径轨迹，图6（b）为删除部分冗余点后生成的路径轨迹，图6（c）为新增节点后生成的路径轨迹，即为本文算法生成的路径。

由表1可知，经过本文的路径优化策略，对比传统A*算法累积转角降低了81.23%，平均转角降低了37.94%，路径长度降低了9.58%。文献[13]与文献[14]对于轨迹仅做了本文路径优化策略的第一步，即只对路径算法做了删除冗余点处理。由表1可知，虽然本文算法在路径长度上相比于文献[13]与文献[14]有少许增加，但是累积均转角与平均转角相比其他文献降低了23.64%和15.82%，使得路径轨迹更加平滑，更符合移动机器人的运动学规律。除此之外，新增的节点缩短了节点间的平均距离，更有利于后续局部路径规划范围的选取。

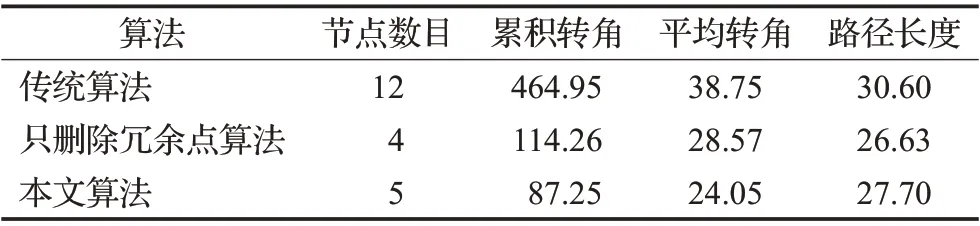
表1 不同算法路径的优化性能比较

图6 优化路径过程

3.1.2 算法效率的比较

Dynamic A*是由Stentz在1994年提出的一种在传统A*算法的基础上发展而来的动态路径搜索算法，一种比较典型的动态路径规划，拥有局部路径规划能力[16-17]。Dynamic A*算法是一种动态环境下的广义A*算法，将其与本文算法比较时间效率与空间效率。

为了减少环境的变化给实验带来的影响，进一步提高实验的客观性，本文采用不同数据在同一台计算机上进行算法仿真模拟，并建立3个不同复杂程度的环境将本文算法与Dynamic A*算法进行比对。环境的复杂程度设定为环境的大小与障碍物的覆盖率，如图7 及表2所示。图7（a）表示环境面积小且障碍物覆盖率低的环境，图7（b）表示环境面积适中、障碍物覆盖率大的环境，图7（c）表示环境面积大、障碍物覆盖率高的环境。

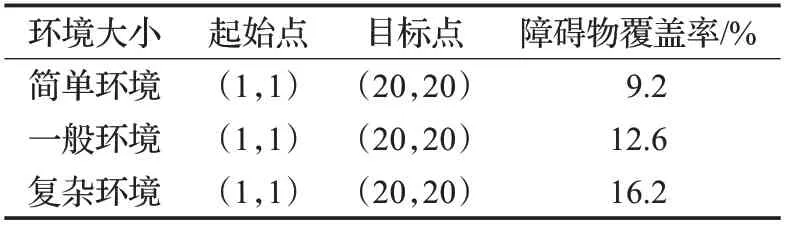
表2 不同复杂程度下的环境参数

如表3 所示，本文从路径规划时间（单位为程序执行的周期次数T）与规划的路径长度两个指标对比Dynamic A*算法与本文算法，可知在20×20的栅格环境下本文算法路径规划时间与路径长度分别减少了12.3%和11.0%，在50×50的栅格环境下本文算法路径规划时间与路径长度分别减少了18.6%和16.4%，在100×100的栅格环境下本文算法路径规划时间与路径长度分别减少了50.4%和49.1%。

实验数据表明，随着栅格环境的增大，环境越复杂，本文算法的优势越加明显。如图8所示，随着环境面积的增加，在栅格数目超过140 左右，Dynamic A*算法所花费的时间与空间将呈指数型增长，而本文算法则在栅格数目超过180后斜率才慢慢增加，理论上也可证实随着环境增大，本文算法效率越来越优于Dynamic A*算法。这是因为A*算法是通过等势线逐级扩展的方式进行搜索，搜索空间较大，这是一种长度优先算法，生成的路径容易在小范围区域内出现多次转弯的现象，环境越复杂，这种现象越加明显[18-19]。而本文算法的路径更新仅发生在每个滚动窗口内，随着空间环境变化，耗费值的增加仅来源于滚动窗口内部路径的变化以及滚动窗口数量的增加，大大降低了路径规划的时间和空间成本。

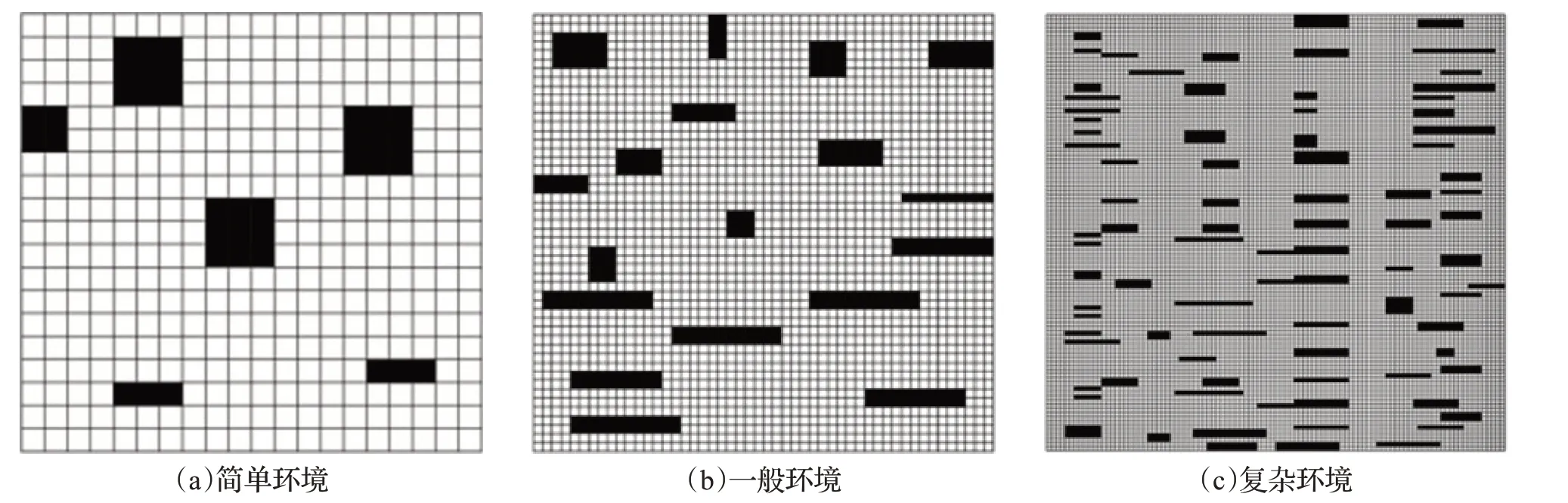
图7 不同复杂程度环境下的栅格地图

表3 不同环境下算法性能对比

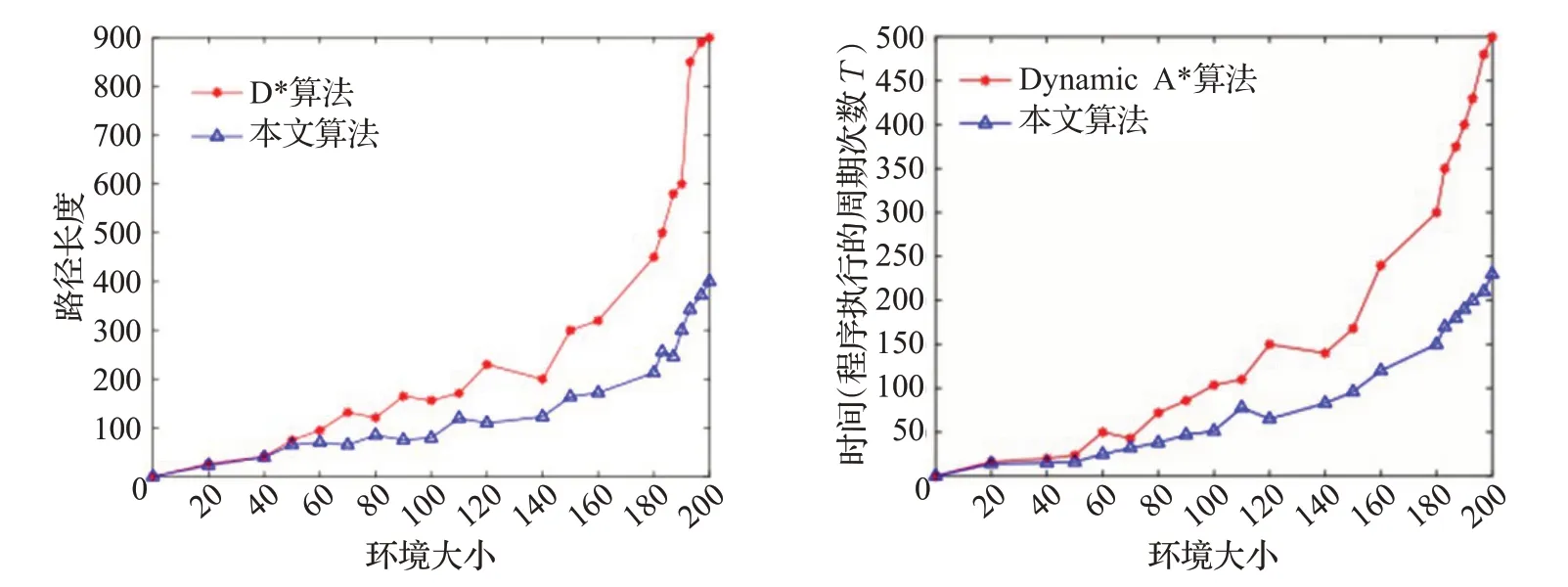
图8 规划时间与路径长度随环境变化折线图

3.2 动态环境仿真

为了验证本文算法的动态规划能力，在算法仿真中引入未先验的动态障碍物，建立简单环境进行仿真验证。在该环境下首先根据先验的地图信息，以S(1,1)为起始点、E(20,20)为终点，进行全局路径规划，优化路径后得到如图9所示的路径，用红线表示。在该路径下选取合适的局部子目标点，增加的局部子目标点数目为2个，设为A、B。

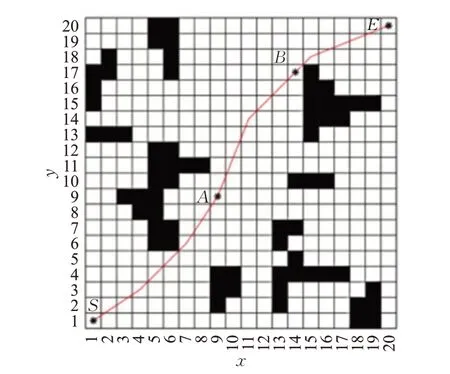
图9 先验环境下的路径

在该环境下路径被分割成3个子路径，分别是SA、AB、BE。机器人在起始位置时，在第一个滚动窗口内未检测到地图信息有变化，机器人沿先验环境下的路径由S 点行进到第一个局部子目标点A。此时，机器人在第二个滚动窗口内检测地图信息，此时检测到动态障碍物M（蓝色方块），根据传感器的信息反馈，机器人将在X 位置（红色栅格）与障碍物相撞，如图10（a）所示。

根据传感器的检测信息，该动态障碍物M 的行进速度小于机器人的行驶速度，M 的行径轨迹与路径轨迹有一个交点，采用慎思型控制结构，在局部区域中重新进行路径规划，更新子路径AB。如图10（b）所示，原路径用虚线表示，机器人的行驶路径用实线表示。当到达第二个子目标点B 时，障碍物位于机器人左侧位置，完成动态避障过程。

表4 为在图9 所示的20×20 的栅格环境下，引入未先验的动态障碍物时不同算法的定量实验比对。传统A*算法不具备避障能力，在遇到未先验的障碍物后路径规划失败，不可到达目标位置。Dynamic A*算法与本文算法在遇到未先验障碍物时，都有重新规划路径的能力，可到达目标位置，且本文算法的规划时间与路径长度相对于Dynamic A*在该实验环境下减少了12.9%与8.1%。

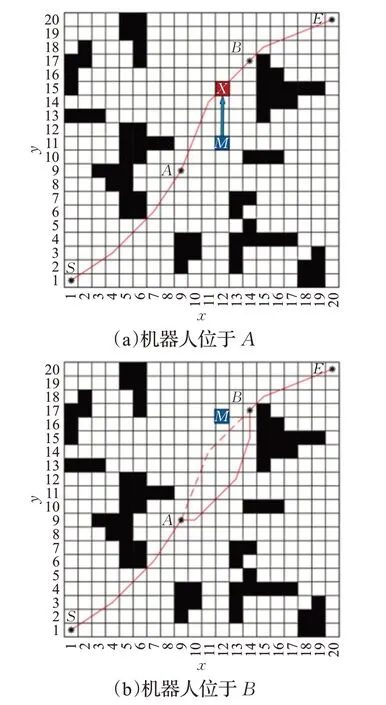
图10 动态避障

表4 动态环境下不同算法比对

4 结束语

传统的A*算法是一种全局的静态路径规划算法，存在路径不平滑、搜索效率低等缺点，本文针对A*算法的不足，提出了一种适用于局部动态环境的路径规划的多重A*算法。多重A*算法首先在原有全局路径之上优化了全局路径轨迹并提取了局部子目标点，在每个滚动窗口内进行局部路径规划，并结合反应型和慎思型避障控制策略的优点进行实时避障。本文将改进后的算法与原算法进行了比对，并在动态环境下进行了仿真分析，在20×20的栅格环境下改进后算法相比于原算法累积转角降低了81.23%，平均转角降低了37.94%，路径长度降低了9.58%，规划时间降低了12.3%，且在未知环境中能有效地避开动态障碍物。