充气薄膜管气-膜耦合作用的有限元分析
王晓峰,付慧杰,杨庆山
(1. 北京交通大学土木建筑工程学院,北京 100044;2. 重庆大学土木工程学院,重庆 400044)
充气薄膜结构具有质量轻、折叠体积小、成本低以及展开可靠性高等优点[1-4],广泛应用于土木工程的大跨建筑结构[3]以及航空航天领域的空间充气天线、充气太阳帆、充气太阳光防护罩、充气居住舱、充气机翼等空间可展结构[3,5-6]。这些空间结构形式多采用充气薄膜管作为主要支撑构件[7-8]。图1 给出了太阳帆中作为支撑构件的充气薄膜管的受力情况:同时受到薄膜帆板(张拉膜)由于太阳光子作用而对其产生的横向均布力F1和由于预张应力而对其产生的轴向力(F2),处于压弯受力状态。

图 1 太阳帆中充气薄膜管承受的荷载Fig. 1 Loads on the inflated membrane tubes in a solar sail
充气薄膜管属于柔性结构,通过内充气压使外围薄膜产生张拉应力而具有刚度和承载能力[3]。荷载作用下,薄膜管的变形会引起内充气体体积及内压改变,进而影响外围薄膜的张拉应力水平和结构的刚度。这种内充气体与外围薄膜的相互耦合作用对充气薄膜管的力学行为具有重要影响。探究充气薄膜管在压弯荷载下的气-膜耦合作用规律有助于深入认识充气薄膜管的力学行为,确保空间充气薄膜结构设计计算的可靠性。
但从现有文献来看,充气薄膜管的研究主要集中在轴向力或轴向拉伸作用下的局部鼓凸问题[9-17]、弯曲荷载作用下的褶皱变形[2,8,18]及其对褶皱临界荷载[5,8,19]和极限承载力的影响[2,18,20]、考虑褶皱影响的自由振动特性[1,18,21-22]、基于多体理论对展开过程的动力学分析[7,23-26]以及外围薄膜的加强方法[27-29]等方面,并通过将内充气压等效为外围薄膜的静力边界条件以考虑内充气体作用的影响,而尚未发现有关充气薄膜管气-膜耦合作用的研究文献。此外,当前文献仅对轴向荷载或弯曲荷载作用下充气薄膜管的力学行为进行了研究,并未关注其在压弯荷载作用下的性能。
鉴于此,本文拟采用有限元方法研究压弯荷载作用下充气薄膜管的气-膜耦合作用及其随影响因素的变化规律。通过将内充气体看做是小扰动线性势流以考虑内充气体与外围薄膜的耦合作用,通过将分析结果与内充气压被等效为外围薄膜静力边界条件情况下的相应计算结果进行对比,研究气-膜耦合作用对充气薄膜管褶皱临界荷载和极限承载力的影响及其随初始内压、长细比、端部约束类型以及轴向荷载的变化情况。
1 理论基础
充气薄膜管的力学行为取决于内充气体和外围薄膜的力学特性以及两者之间的耦合作用,因此可通过内充气体和外围薄膜的平衡方程以及气-膜耦合作用方程进行描述。
1.1 内充气体平衡方程
充气薄膜管中内充气体属于封闭流场,且荷载作用下引起的扰动速度很小,因此可假定其为均匀、无旋、无粘的理想流体,并且在变化过程中始终满足等熵条件。
这样,内充气体可看做为线性有势流体[30],在小扰动条件下满足以速度势 φ为基本场变量的小幅波动方程[31]


1.2 外围薄膜平衡方程
假定薄膜具有微小的抗弯刚度,其褶皱变形可以看作是压应力作用下发生的局部屈曲,可借助板壳稳定理论通过非线性屈曲分析求得。同时,假定薄膜变形符合大转动、小应变特征[32],且在整个变形中应力-应变关系满足广义虎克定律。
这样,其平衡微分方程可以写为[33]:

1.3 气-膜耦合作用方程
内充气体和外围薄膜耦合界面处,在不考虑内充气体粘性的情况下,有:


式(7)和式(8)即为考虑内充气体与外围薄膜耦合作用的充气膜有限元模型。
2 有限元模型
根据上述建立的充气薄膜管气-膜耦合作用方程,本文采用商用有限元软件ADINA,通过八结点线性势流单元对内充气体进行离散以考虑气-膜耦合作用的影响;基于板壳稳定理论、通过假定外围薄膜为Kirchhoff 材料以考虑褶皱影响及大转动、小应变的变形特点。充气薄膜管的外围薄膜和两端盖板均采用四结点薄壳单元进行离散。
经过不同网格密度情况下的数值结果比较,综合考虑计算精度和计算时间,最终确定外围薄膜的单元尺寸为3.93 mm×7.00 mm,共计8000 个薄膜单元;内部势流单元尺寸为(2.91 mm~3.93 mm)×(2.91 mm~3.93 mm)×7.00 mm,共计84 400 个单元;两端盖板的单元尺寸为(2.91 mm~3.93 mm)×(2.91 mm~3.93 mm),共计844 个单元。建立的有限元模型如图2 所示。

图 2 充气薄膜管的有限元模型Fig. 2 Finite element model of the inflated membrane tube
本文拟采用该有限元模型,分析充气薄膜管在图3 所示压弯荷载作用下的气-膜耦合作用。竖向荷载Fz作用在充气薄膜管上端,横向荷载Fx作用在其长度的三分点处。在给定的竖向荷载作用下,不断增加横向荷载直至达到充气薄膜管的极限承载力。两端的约束均分别考虑了固定和简支两种情况。通过约束充气薄膜管端部盖板作为刚性平面的三个平动和三个转动自由度以考虑固定约束的影响;通过约束端部盖板作为刚性平面的三个平动自由度和绕x轴和z轴的转动自由度以考虑简支约束的影响。由于充气薄膜管的上端受竖向荷载作用(图3 所示),因此上部盖板在固定和简支约束情况下均释放沿z向的平动自由度。

图 3 充气薄膜管荷载作用示意图Fig. 3 Diagram of the inflated membrane tube under load
充气薄膜管外部薄膜采用Kapton 膜材,内充气体为空气,两端采用铝制盖板封闭①由于试验中充气薄膜管两端采用铝制盖板封闭,为保证材性的一致性以便于对比验证,充气薄膜管的数值模型中端部盖板也设置为铝材。,相应的材料参数如表1 所示。

表 1 充气薄膜管的材料参数Table 1 Material properties of the inflated membrane tube
具体有限元分析过程如下:
1) 形态分析:通过对充气薄膜管的势流单元施加质量流荷载使内充气体达到初始内压。
2) 施加初始缺陷:对充气薄膜管进行特征值屈曲分析,并将第一阶特征值屈曲模态乘以10-8作为初始缺陷施加到有限元模型上。
3) 对轴向和横向荷载作用下的充气薄膜管进行非线性屈曲分析②本文在计算中假定屈曲后刚度退化到初始刚度的5%便达到极限状态(详见第四章第二段),并未计算至屈曲后的负刚度阶段,因此通过设置较小的荷载增量(0.5 N),采用常规的收敛设置,即牛顿迭代结合线性搜索算法以及能量收敛准则,可以使得每一时间步计算收敛。,求解褶皱临界荷载和极限承载力。
3 有限元模型验证
作者拟通过静力试验验证本文建立的考虑气-膜耦合作用的有限元模型的正确性和精确性。由于现有的试验设备无法满足试验加载和测量的精度要求,作者根据图3 所示的荷载和约束条件,专门研发了充气薄膜管压弯试验装置,如图4 所示。试验中,通过砝码施加竖向和横向荷载;位移和内压分别采用松下HG-C1100 激光位移计和数字差压计进行量测;充气设备为220 V 单缸充气泵,并在排气口位置处安装活塞用于气压微调,确保初始气压的精度,充放气系统示意图如图5 所示。

图 4 试验装置实物图Fig. 4 Experimental setup
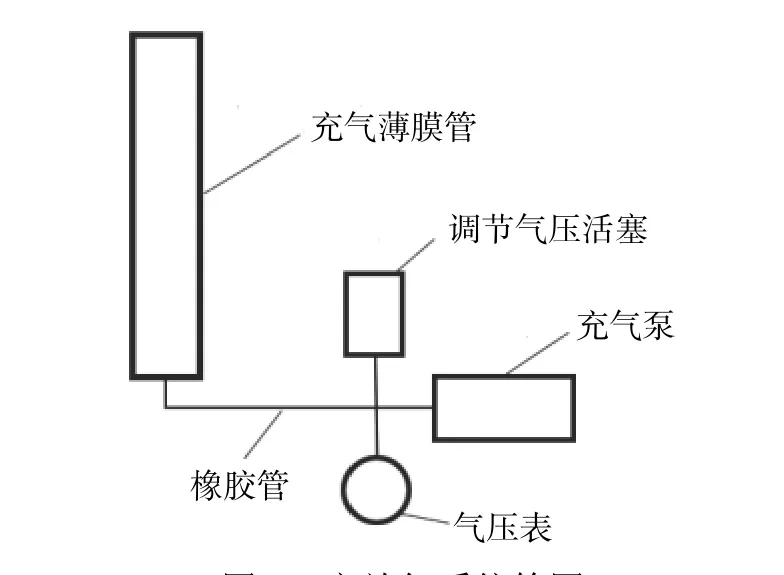
图 5 充放气系统简图Fig. 5 Diagram of the inflating and deflating system
充气薄膜管试验将内充气体分为恒质量和恒压两种情况,分别用于验证将内充气体等效为线性势流和外围薄膜静力边界条件的有限元模型。试验中,内充气体为恒质量的情况是通过在加载过程中使内充气体始终保持密闭实现;而对于内充气体为恒压情况,则在加载过程中通过放气使内充气压保持不变。
图6 给出了充气薄膜管在直径100 mm、长细比为7、膜厚75 μm、两端固定、轴向荷载为10 N以及内充气压为6 kPa 情况下试验与数值的对比结果。图6(a)与图6(b)分别是内充气体为恒质量和恒压的情况。

图 6 横向荷载与横向位移关系曲线Fig. 6 Transverse-load vs. transverse-displacement curves
图7 给出了与图6 相同工况下,充气薄膜管在极限状态时分别由试验和有限元分析得到的变形图。

图 7 充气薄膜管的变形图 /mmFig. 7 Deformation of the inflated membrane tube
从图6 及图7 给出的对比结果可以看出,由有限元分析得到的荷载-位移曲线以及极限状态时的变形均与试验结果吻合很好,从而验证了本文建立的充气薄膜管有限元模型的正确性和精确性,可用于充气薄膜管气-膜耦合作用的有限元分析。
4 气-膜耦合作用
通过将内充气体分别等效为线性势流和静力边界条件情况下的有限元分析结果进行对比,研究气-膜耦合作用对充气薄膜管在压弯荷载作用下(轴向荷载不变,不断增加横向荷载直至破坏)的褶皱临界荷载和极限承载力的影响及其随初始内压、长细比、端部约束以及轴向荷载的变化规律。各影响因素取值范围以及其他参数取值情况如表2 所示。

表 2 影响因素的取值范围及其他参数取值情况Table 2 Ranges of the influencing factors and values of the other parameters
充气薄膜管在图3 所示的压弯荷载作用下,随着横向荷载的增加(轴向荷载不变),跨中受压侧首先出现褶皱。本文将充气薄膜管刚刚发生褶皱所对应的横向荷载确定为褶皱临界荷载③在试验和数值分析中作者发现充气薄膜管在压弯荷载作用下跨中褶皱总是突然出现,并且褶皱角(即横截面上褶皱区域所对圆心角)已为60°左右,因此将跨中褶皱角为60°时对应的横向荷载为褶皱临界荷载。。充气薄膜管在褶皱出现后,随着横向荷载的增加,褶皱变形逐渐增大,横向刚度逐渐降低。当其横向刚度④横向刚度和初始刚度均指切线刚度。某一级横向荷载对应的切向刚度由该级荷载增量与跨中相应的横向位移增量的比值近似确定。物理试验中,采用激光位移计测量充气薄膜管跨中的横向位移,采用砝码逐级施加横向荷载,也是采用上述同样的方法近似确定横向切线刚度。减小到初始刚度的5%时,本文认为已经达到其极限状态,将此时对应的横向荷载确定为极限荷载,即充气薄膜管的极限承载力。为了保证充气薄膜管最终是发生整体压弯破坏,而不是因横向集中荷载作用位置处外围薄膜的局部褶皱变形而导致的迅速破坏,采用与试验相同的方法沿充气薄膜管环向180°范围内施加宽度为3 cm 面荷载代替集中荷载,如图8 所示。

图 8 充气薄膜管的横向荷载Fig. 8 Transverse loads on the inflated membrane tube
4.1 初始内压的影响

从图9(a)和图9(b)可以看出,气-膜耦合作用对充气薄膜管褶皱临界荷载和极限承载力的影响随初始内压的变化呈现先减小后增大的非单调特点。气-膜耦合作用体现为外围薄膜变形与内充气压之间的相互作用。因此外围薄膜的变形及其引起内充气压的变化程度均会影响气-膜耦合作用。
随着初始内压的升高,充气薄膜管的横向刚度增大,横向变形减小,由此引起内充气体的体积改变量逐渐减小,因而内充气压的改变量有减小的趋势;另一方面,随着初始内压的升高,内充气压对内充气体体积改变越敏感,因而内充气压的改变量有增大的趋势。在这两种趋势的共同影响下,气-膜耦合作用对褶皱临界荷载和极限承载力的影响随初始内压非单调变化。

图 9 气膜耦合作用随内压的变化曲线Fig. 9 Variation of the air-membrane interaction with the initial inner pressure
在褶皱临界阶段,当初始内压在小于7 kPa 的范围内增加时,内充气体体积变形减小的速度快,而内充气压随初始内压的升高而对体积变形的敏感性增加速度较慢,所以内充气压改变量减小,气-膜耦合作用对褶皱临界荷载的影响减弱,图9(a)中相应曲线段呈现下降的趋势。当初始内压在大于7 kPa 的范围内增加时,内充气压对内充气体体积改变的敏感性较快增强,虽然内充气体体积的变形量继续减小,但内充气压的改变量增大,因而气-膜耦合作用对褶皱临界荷载的影响增强,图9(a)中相应曲线段呈上升的趋势。
基于同样的原因,在极限阶段,当初始内压在小于6 kPa 的范围内增加时,气-膜耦合作用的影响降低,图9(b)中相应曲线段呈下降的趋势,当初始内压在大于6 kPa 的范围内增加时,气-膜耦合作用的影响增强,图9(b)中相应曲线段呈上升的趋势。
在极限阶段,充气薄膜管的变形远大于褶皱临界阶段,所以气-膜耦合作用由于内充气压对体积变形的敏感性而随初始内压升高开始增强的位置(即图9(b)曲线的极小值位置,对应的初始内压为6 kPa)要前于褶皱临界阶段的相应位置(即图9(a)曲线的极小值位置,对应的初始内压为7 kPa)。而且极限阶段的气-膜耦合作用随初始内压的升高经过极小值后,由于充气薄膜管的变形远大于褶皱临界阶段的变形,因而增强速度较快,所以图9(b)曲线的上升段要比图9(a)曲线的上升段陡峭。
4.2 长细比的影响
图10 给出了气-膜耦合作用随充气薄膜管长细比的变化曲线,图中λ 为长细比。

图 10 气膜耦合作用随长细比的变化曲线Fig. 10 Variation of the air-membrane interaction with the slenderness ratio
从图10(a)可以看出,气-膜耦合作用对充气薄膜管褶皱临界荷载的影响随长细比的变化呈现先增大再减小又增大的非单调特点,在长细比的变化范围内,出现极大值和极小值。从图10(b)可以看出,气-膜耦合作用对充气薄膜管极限承载力的影响随长细比的变化也呈现出非单调的特点,但变化规律与图10(a)不同,表现为先减小,后增大,仅出现极小值。图10(a)和图10(b)所示曲线非单调变化特点以及两者变化差异的主要原因是充气薄膜管在褶皱临界阶段和极限阶段,轴力二次效应和气-膜耦合作用的影响所占比重不同以及随长细比的变化快慢不同导致。当充气薄膜管在压弯荷载作用下的变形主要体现为轴线的弯曲变形,而体积变形(由横截面因变形而面积减少以及轴线缩短引起)较小时,轴力二次效应占主导地位,反之则气-膜耦合作用占主导地位。当充气薄膜管轴线弯曲变形的增加速度大于体积变形的增加速度,则轴力二次效应增大速度快于气-膜耦合作用的增大速度,反之则气-膜耦合作用的增大速度快于轴力二次效应的增大速度。
对于受压弯荷载作用的充气薄膜管,将内充气体等效为线性势流(考虑气-膜耦合作用)和静力边界条件(不考虑气-膜耦合作用),均存在轴力二次效应,所以当轴力二次效应占主导地位时,两者计算结果差异小;当气-膜耦合作用占主导地位时,两者的计算结果差异大。随长细比的增加,当轴力二次效应增大速度大于气-膜耦合作用的增大速度时,两者计算结果的差异呈减小的趋势;当气-膜耦合作用的增大速度快于轴力二次效应的增大速度时,两者计算结果的差异呈增大的趋势。
当长细比小于7 时,随着长细比的增加,充气薄膜管在褶皱临界阶段的变形逐渐增大,但其轴线弯曲变形较小,而主要体现为体积变形以较快速度增加,使得气-膜耦合作用增加速度大于轴力二次效应增加速度,且逐渐占主导地位,因此将内充气体等效为线性势流和静力边界条件得到的褶皱临界荷载差异增大,图10(a)所示曲线在这个区间呈上升的趋势。由于充气薄膜管在极限阶段的轴线弯曲变形较大,且长细比在这个范围内增加时,弯曲变形的增大速度大于体积变形的增大速度,使得轴力二次效应增加较快并逐渐占主导地位,所以图10(b)所示曲线在这个区间呈下降的趋势。
当长细比在7~9 的范围内增加时,充气薄膜管在褶皱临界阶段的弯曲变形增加速度开始超过体积变形的增加速度,使得轴力二次效应与气膜耦合作用相比以较快速度增加,所以图10(a)所示曲线在这个区间呈下降的趋势。当长细比增加超过9 后,褶皱临界阶段体积变形的增加速度又超过弯曲变形增加速度,使得气-膜耦合作用的增加速度快于轴力二次效应增加速度,所以图10(a)所示曲线在这个区间呈现再上升的趋势。而在极限阶段,当长细比在大于7 的范围内增加时,充气薄膜管的体积变形的增大速度始终较快,使得气-膜耦合作用的增加速度大于弯曲变形的增加速度,并逐渐占主导地位,所以图10(b)所示曲线在这个区间呈持续上升的趋势。
4.3 端部约束的影响
图11 给出了气-膜耦合作用随充气薄膜管端部约束的变化情况,图中F-F 表示两端固定,F-S 表示一端固定一端简支,S-S 表示两端简支。气-膜耦合作用对褶皱临界荷载和极限承载力的影响在充气薄膜管一端固定一端简支时最强,而两端简支时最弱,两端固定时略大于两端简支的情况。
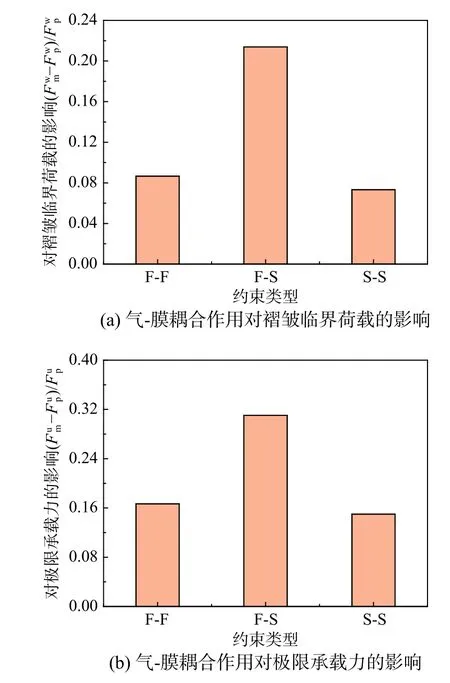
图 11 气膜耦合作用随端部约束的变化Fig. 11 Variation of the air-membrane interaction with the end constraints
当两端为固定约束时,充气薄膜管在压弯荷载作用下变形较小,引起内充气体体积及气压改变量小,所以气-膜耦合作用对褶皱临界荷载和极限承载力的影响较弱;对于两端简支的情况,与其他两类约束相比约束程度最弱,在很小的压弯荷载作用下迅速达到极限承载力,整个过程中变形因没有来得及充分发展而很小,所以内充气体体积及内压改变量最小,气-膜耦合作用最弱。而一端固定一端简支的约束程度适中,充气薄膜管在达到褶皱临界荷载以及极限承载力时,变形均有较充分的发展,内充气体体积及内压改变量显著,因此气-膜耦合作用最强。
4.4 轴向荷载的影响
图12 给出了气-膜耦合作用随轴向荷载的变化曲线,图中Fz为轴向荷载,A为充气薄膜管的横截面面积。

图 12 气膜耦合作用随轴向荷载的变化曲线Fig. 12 Variation of the air-membrane interaction with the axial compression
从图12(a)可以看出,气-膜耦合作用对充气薄膜管的褶皱临界荷载的影响随轴向荷载的变化呈现增大→减小→增大→减小的非单调特点,在轴向荷载的变化范围内,出现两个极大值和一个极小值。而气-膜耦合作用对充气薄膜管极限承载力的影响则呈现增大→减小→增大的非单调特点,在轴向荷载的变化范围内,出现一个极大值和一个极小值,如图12(b)所示。
气-膜耦合作用出现如图12(a)和图12(b)所示曲线的非单调变化以及两者变化存在差异的主要原因类似4.2 节,即由于充气薄膜管在褶皱临界阶段和极限阶段,轴力二次效应和气-膜耦合作用的影响作用所占比重不同以及随轴向荷载的变化快慢不同导致。
当轴向荷载Fz在小于0.42P0A的范围内增加时,由于轴力相对较小,轴力二次效应增长较慢,而内充气体的体积变形以较快速度增加,使得气-膜耦合作用快速增强,且逐渐占主导地位,因此图12(a)和图12(b)所示这部分曲线呈上升趋势。
当轴向荷载Fz在(0.42~0.85)P0A的范围内增加时,充气薄膜管在褶皱临界阶段的弯曲变形增长速度超过了内充气体体积变形的增长速度,轴力二次效应出现较快增强,而气-膜耦合作用影响减弱,因此图12(a)所示这部分曲线呈下降趋势。当轴向荷载Fz在(0.85~1.27)P0A以及大于1.27P0A的范围内增加时,同样由于气-膜耦合作用和轴力二次效应的交替快速增加,图12(a)所示这段曲线呈现先上升后下降的特点。
当轴向荷载Fz在(0.42~1.27)P0A以及大于1.27P0A的范围内增加时,极限阶段的轴力二次效应和气-膜耦合作用也是交替快速增加而使得图12(b)所示这段曲线呈现先下降后上升的特点。
由于充气薄膜管在极限阶段的变形大于褶皱临界阶段的变形,导致在这两个阶段轴力二次效应和气-膜耦合作用随轴向荷载交替出现快速增加的规律存在差异,所以图12(a)和图12(b)所示气-膜耦合作用的变化曲线呈现不同的变化特点。
5 结论
本文采用商用有限元软件ADINA,通过将内充气体作用分别等效为线性势流和静力边界条件情况下的分析结果进行对比,研究了气-膜耦合作用对充气薄膜管褶皱临界荷载和极限承载力的影响及其随初始内压、长细比、端部约束以及轴向荷载的变化规律。取得的主要结论如下:
(1) 气-膜耦合作用随初始内压的升高呈现先减弱后增强的非单调特点,在初始内压的变化范围内存在极小值。
(2) 随长细比的增加,气-膜耦合作用对褶皱临界荷载的影响呈现先增大再减小又增大的非单调特点,在长细比的变化范围内,出现极大值和极小值;而气-膜耦合作用对极限承载力的影响随长细比的增加先减小后增大,仅存在极小值。
(3) 端部约束类型对气膜耦合作用有重要影响,一端固定一端简支情况下气-膜耦合作用最强,而两端简支条件下气-膜耦合作用最弱,两端固定约束情况下气-耦合作用略大于两端简支的情况。
(4) 气-膜耦合作用对褶皱临界荷载的影响随轴向荷载的变化呈现增大→减小→增大→减小的非单调特点,在轴向荷载的变化范围内,出现两个极大值和一个极小值;气-膜耦合作用对极限承载力的影响随轴向荷载的增加先增大再减小然后又继续增大,出现一个极大值和一个极小值。
气-膜耦合作用对充气薄膜管的力学行为具有显著影响。考虑气-膜耦合作用得到的褶皱临界荷载和极限承载力与相同情况下不考虑气-膜耦合作用的计算结果相比,最大差值分别为50%和87.5%,只有个别情况下两者的结果差异小于5%。因此,在充气薄膜管的有限元分析中,均应考虑气-膜耦合作用的影响,这样才能准确反映其力学行为。本文的研究成果有助于提高充气薄膜管计算分析的精确性,从而保证其设计的合理性和可靠性。

