河流弯道角度和流量对河流弯道冲刷影响研究

贺丽丽 郭向红 赵俊刚 全炳欣 梁世春

（1.太原理工大学水利科学与工程学院 山西太原030024；2.山西省交通规划勘察设计院有限公司 山西太原030012）

随着社会经济的发展，我国公路建设规模越来越大。不少公路路段由于地形限制与河道并行，存在沿河公路路基侵占河道、压缩河床过水断面，致使河道中水位升高，流速增大，河道冲刷加剧等问题出现[1]。天然河道弯曲型居多，水流进入弯道后，由于离心力的存在，水流改变原有平稳的流态，凹凸两岸出现水面横向比降，并在顺水流方向不断改变，出现三维螺旋流[2]。河流弯道独特的水流特性也使得弯道中泥沙的运输也变得复杂，位于河流弯道的泥沙常常出现两岸不同程度的冲刷或者凹岸冲刷凸岸泥沙淤积的现象[3]。位于河道凹岸的公路路基边坡和坡脚很容易被水流冲刷致使河床的不断下切，造成路基土体流失，以致变形垮塌[4-6]。所以，合理确定路基防护物基础埋深的大小显得十分重要。因此，本文运用物理模型试验，研究河道流量和弯道角度对河流弯道冲刷深度的影响，为沿河公路路基冲刷计算提供理论支持。

1 材料与方法

1.1 试验系统

试验在太原理工大学水流试验大厅进行，试验系统布置如图1 所示。试验系统由进水箱、河道、退水箱、循环管道构成，进、退水箱及河道均由有机玻璃制成，进水箱体积为1.5 m×1 m×1.2 m，河道由直段和三组弯段（15°、30°、45°）组成，河道断面为矩形断面，规格为0.3 m×0.3 m，二者依靠法兰连接成完整的河道，退水箱体积为1.8 m×1 m×1.15 m，循环输水管道则是由钢管制成，连接进退两水箱，按照直径不同分为D50 和D100 两种方便输送不同流量大小的水流。

图1 试验系统布置图

试验时将一定高度的泥沙平铺在河道内，水从输水管输入进水箱，待进水箱水位达到河道高度时，由阀门控制水流流入河道，对河道内的泥沙进行冲刷。进水箱与河道连接处设有稳流装置，以达到水流流态平稳，同时在河道入口处装有三角堰用于挡沙。渠道末端和退水箱相连，由进水箱内的水携带河道中的泥沙一并进入退水箱中，箱中设有泥沙过滤装置，水流经退水箱过滤后由循环输水管道中的水泵抽出经钢管回流到进水箱，形成一个封闭循环系统，经过滤后泥沙可再次使用。

1.2 试验方案

本试验研究的目的是分析不同流量和不同弯道角度下河道冲刷深度。因此，试验以流量和弯道角度为控制因素，设置几个不同流量水平，即10、15、20、25、30、35、40、45、50 m3/h，三个弯道角度，即15°、30°、45°，共27 组试验。试验用沙为非均质天然沙，图2 为试验选用天然沙级配图，其中d50=0.94 mm，γ=2 650 N/m3。

1.3 测点布置与测试项目

图2 天然泥沙级配表

试验测量主要集中在河道直段及弯段中进行，河道长7.5 m，直段长6 m，弯段长1.5 m。如图3 所示天然沙冲刷试验中沿程共设置了9 个断面。直段部分设置4 个断面，分别为断面1（0 m）上游直段入口、断面2（0+1.5 m）上游直段中部、断面3（0+3.5 m）上游直段中部、断面4（0+5.0 m）上游直段下部。弯段部分设置4 个断面分别为断面5（0+5.6 m）弯段入口处、断面6（0+5.85 m)弯顶处、断面7（0+6.1 m)弯道出口处及断面8（0+6.5 m）弯段出口下游处。下游直段中部设置断面9（0+7.1 m）。

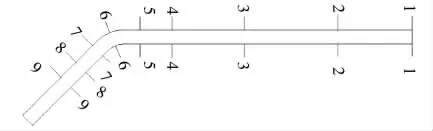
图3 天然沙河道测点布置图

河道流量采用电磁流量计测量，通过阀门调节循环输水管道中进入进水箱中的水流流量，继而控制流入河道的水流流量。河道中泥沙冲刷深度的测量选用钢针和钢尺测量，其中钢针测量精度较高（0.001 m），每次试验水流冲刷结束后，利用钢针测量各个测点凹岸和凸岸河床的高度，与该测点冲刷前河道中铺沙高度的差值计算出该测点泥沙冲刷的深度。

1.4 数据分析

试验数据处理采用excel，绘图采用origin2019，公式拟合采用1stOpt1.5pro 软件。

2 结果与分析

2.1 河流流量对河流弯道冲刷深度影响分析

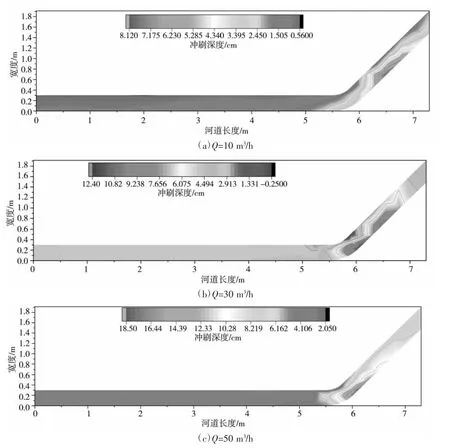
图4 不同流量下河道冲刷深度二维分布图

图4 为弯道角度45°不同流量下河道冲刷深度二维分布图。由图可知，不同流量下河道冲刷深度分布规律相似，即，在顺直河段，河道冲刷深度均匀，且较小；在弯道河段，河道凹侧泥沙冲刷深度顺水流方向呈现先逐渐增大，出弯道后逐渐减小的现象，弯道凸侧冲刷深度较小或出现了淤积现象，河道凹侧冲刷深度大于凸侧冲刷深度，河道最大冲刷深度出现在河道凹侧弯顶的下游。这是由于在水流在弯道部分形成弯道环流，造成河道凹岸冲刷，凸岸淤积。进一步分析可知，河流流量对河道各段冲刷深度有一定的影响。在顺直河段，随着流量的增大，冲刷深度也逐渐增大，例如：水流流量Q=10 m3/h 时，天然沙冲刷深度约为0.5 cm；流量Q=50 m3/h 时，天然沙冲刷深度约为4 cm。在弯道河段，沿程泥沙冲刷深度均随流量的增大而增大。图4 中，弯道角度为45°条件下，流量由10 m3/h 增至50 m3/h，弯道出口处凹侧最大冲刷深度由4.72 cm逐渐增至18.48 cm，增幅近三倍。这是由于水流进入弯道后受凹侧路基阻挡，水流形态发生改变，在弯段凹侧产生沿水流方向顺时针螺旋流，具有较强的切应力，大量床沙成为悬移质被水流携带走，造成弯道凹侧局部冲刷。随着流量增大，水流流速也随之增大，水流冲击能力增强，凹侧冲刷深度也随之增大。

2.2 河流弯道角度对河流弯道冲刷深度影响分析

图5 为不同弯道角度条件下河流冲刷深度情况。由图分析可知，不同弯道角度下，弯道冲刷分布规律一致，均为凹岸冲刷，凸岸淤积，但弯道角度对冲刷深度有一定影响，随弯道角度的增加，河流弯道凹侧泥沙冲刷深度也增大。在图5 中，流量为50 m3/h 时，弯道角度由15°增大至45°，弯道最大冲刷深度由5.83 cm升至18.43 cm，增幅高达216%。这是由于随着弯道角度的增大，河流弯道环流发育越充分，水流冲击能力增强，凹侧冲刷深度也随之增大。

2.3 流量和弯道角度对河流弯道冲刷最大深度影响分析

图6 为河流弯道角度和流量交互作用对河道冲刷深度影响。由图可知，在同一流量下，最大冲刷深度随着弯道角度的增大而增大，在同一弯道角度下，最大冲刷深度对照流量的增大而增大，弯道角度和流量的交换作用，增大了河流弯道的冲刷深度。

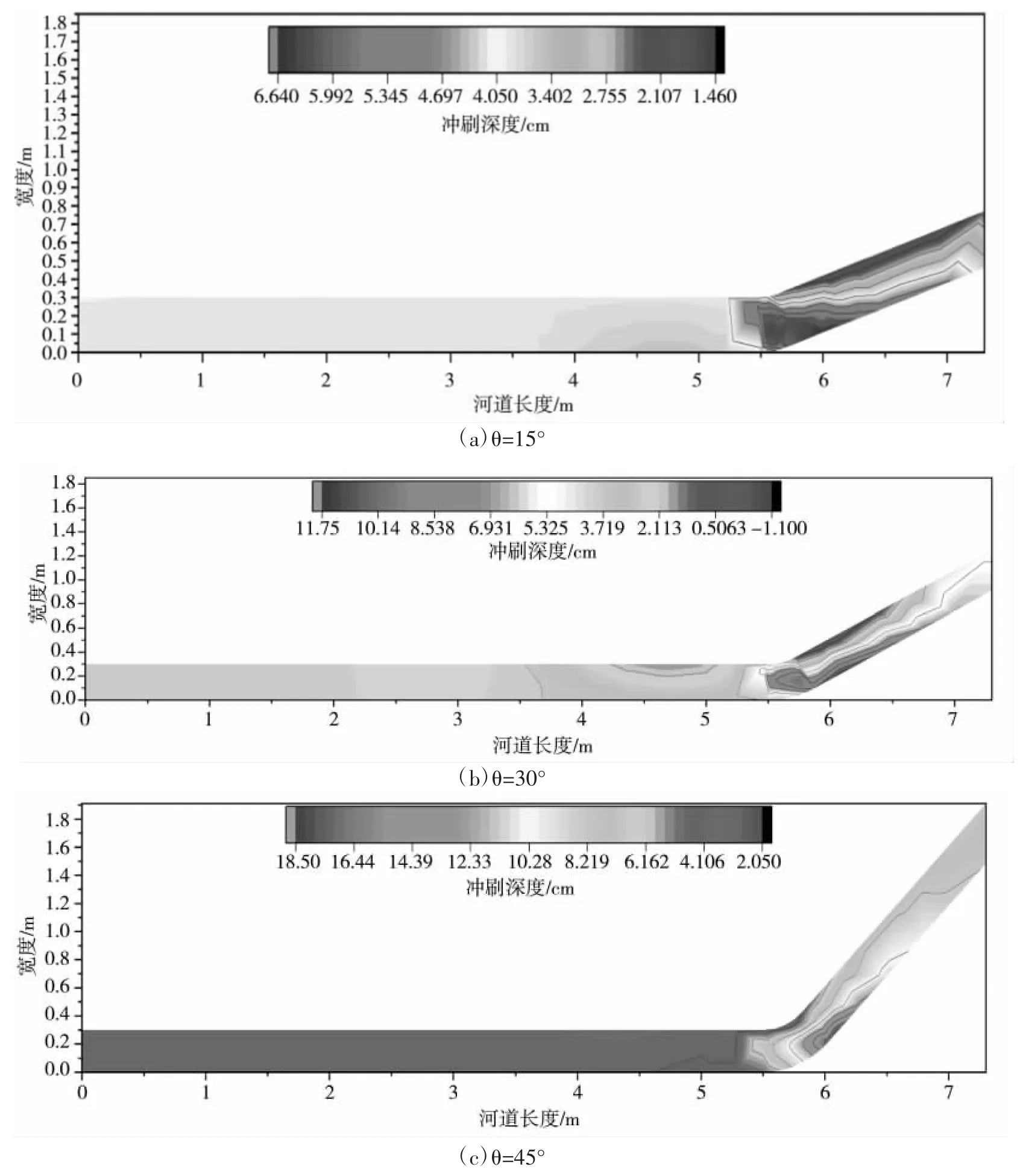
图5 不同弯道角度下河道冲刷深度二维分布图

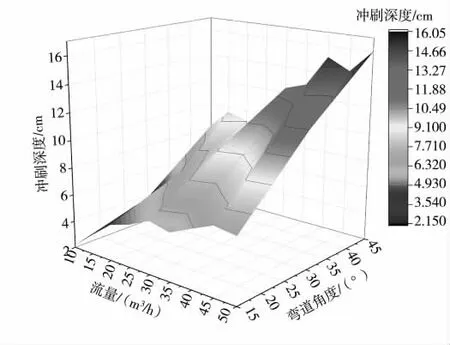
图6 河流弯道角度和流量交互作用对河道冲刷深度影响

进一步，采用式（1）形式的多元乘幂函数对弯道最大冲刷深度与流量和弯道角度的关系进行拟合，拟合结果为： 拟合参数a、b、c 分别为0.102 6、0.555、0.756 5，相关系数R 为0.981。这说明河流弯道最大冲刷深度与流量和弯道角度的关系，可以采用式（1）的多元乘幂函数表示。

式中：hmax——河流弯道泥沙最大冲刷深度，cm；

Q——流量，m3/h

θ——弯道角度，°；

a、b、c——拟合参数。

3 结论

本文通过对不同流量和弯道角度对河道冲刷深度的影响分析，得出以下结论：1）顺直河段河流冲刷深度较小且均匀，河流弯道凹岸冲刷深度较大，而凸岸冲刷深度较小；2）河流流量和弯道角度对河道冲刷深度有一定的影响，随着流量和弯道角度的增大，顺直河段和弯道河段的冲刷深度均增大；3）河流弯道最大冲刷深度与流量和弯道角度呈多元乘幂关系。