基于MATLAB App Designer的非饱和土壤入渗数值仿真实验研究

郭向红 马娟娟 肖 娟 周义仁 曹玉涛 雷 涛 郑利剑

（太原理工大学水利科学与工程学院 山西太原030024）

土壤入渗是指水通过土壤表面进入土壤内容的过程。降雨、灌溉水只有通过入渗才能将集中水流转化为非饱和土壤水，被作物吸收利用[1,2]。非饱和土壤入渗特性实验是《农田水利学》课程必修实验，实验2学时。但是由于实验仪器台套数、场地和时间的限制，在2 h 的实验中，学生仅仅只能进行一种土壤在特定的容重和初始含水率下的土壤入渗特性实验。而实际中，土壤的入渗特性受土壤质地、容重、初始含水率等影响，有很大的变化。为了补充物理实验的不足，采用“虚实结合”的方法，基于农田水分运动基本方程，开发非饱和土壤的入渗特性试验仿真软件，解决仪器台套数、场地和时间的限制，使学生理解不同土壤质地、容重、初始含水率条件下土壤入渗特性。

1 非饱和土壤入渗特性模型

1.1 基本方程

根据土壤水分运动理论，非饱和土壤入渗可以采用土壤水分运动方程表述，同时，为了使方程具有通用性，选用混合型土壤水分运动的基本方程，可以描述为[3-5]：

式中：h——负压水头，cm；

θ——土壤体积含水量，cm3/cm3；

K（h）——非饱和导水率，cm/min；

z——空间坐标，cm；

t——时间，min。

1.2 定解条件

初始条件：

式中：h0（z）——土柱内任意位置处土壤的初始负压水头，cm；

hst——土壤初始含水率θ0对应的负压水头，cm。

边界条件：

1）上边界条件：

非饱和土壤入渗，地表有一定厚度的积水，所以上边界为一类边界条件：

式中：h——负压水头，cm；

h0——入渗水头，cm。

2）下边界条件：

式中：L——最大计算深度，cm。

2 数学模型的离散

采用有限差分法对方程进行离散，结果式（5），求解式（5）便可以得到土壤水分分布[5]。

式中：i——距离结点编号；

j——时间结点编号，j、j+1 分别表示前一计算时刻和当前计算时刻；

k——表示在某一时刻，计算的迭代次数。

3 软件开发与功能演

由于本软件计算部分为方程组系数矩阵组装、方程求解，选择擅长矩阵计算的Matlab2019 作为计算开发语言。可视化部分主要实现不同土壤类型、容重和初始含水率设置，图形动态显示水分入渗过程、入渗参数与时间关系，所以选用MATLAB App Designer 进行设计。App Designer 可以通过拖放可视化组件布局图形用户界面（GUI），并使用集成编辑器快速编程其行为，建专业的应用程序，并将MATLAB 应用程序打包成一个单独的文件，可以很容易方便其他用户使用。软件界面如图1。

软件启动后主界面如图1 所示。主界面由3 部分组成。

第一部分：选择与控制部分，该部分位于软件的左侧。其中左上部分可以用来选择模拟土壤类型，包括壤土、黏土、砂土；模拟土壤的初始含水率，包括高、中、低；模拟土壤的容重，包括大、中、小。左侧下部是控制按钮，点击【运行】可以进行自动计算选择条件下土壤的入渗过程。其余按钮为保存结果按钮，可根据需要分别保存图像和数据。

第二部分：结果显示部分，位于软件的中部。在【含水率图和湿润锋图】选项卡下单击【运行】按钮软件可以动态显示土壤含水率的分布和湿润锋的推进过程，如图1 所示。在【入渗率与累积入渗量图】选项卡下，可以显示土壤入渗率和累积入渗量随时间的变化过程，如图2 所示。

图1 软件【主界面】

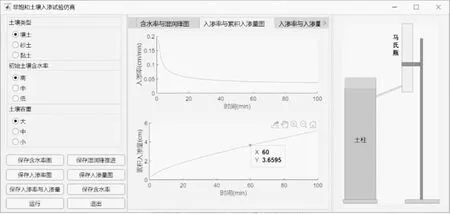
图2 【入渗率与累积入渗量图】选项卡下软件界面

图3 【入渗率与累积入渗量数据】选项卡下软件界面

图4 【含水率数据】选项卡下软件界面

在【入渗率与累积入渗量数据】选项卡下，可以显示土壤入渗率和累积入渗量随时间的变化的具体数据，如图3 所示。

在【含水率数据】选项卡下，可以显示不同时间土壤含水率的具体数据，如图4 所示。

第三部分：物理模型示意图，位于软件的右侧，主要是展示室内非饱和土壤入渗试验模型。

通过以上功能，便可让学生掌握不同土壤类型、初始土壤含水率、土壤容重条件下土壤入渗过程、入渗率曲线、累积入渗量曲线，并把数据导出供学生进一步分析。

4 结语

本文根据土壤水动力学原理，建立了一维非饱和土壤入渗模型，采用差分法离散，MATLAB App Designer 进行编程和界面设计，开发了非饱和土壤入渗试验仿真软件，该软件实现了不同土壤类型、土壤容重、土壤初始含水率下土壤入渗过程、入渗率动态变化、累积入渗量动态变化的可视化，为学生全面掌握土壤入渗特性提供支持。