浅析基于微波双缝干涉的波长测量

徐碧浩 王子健 罗世尚 何 新* 杨俊波

（1、国防科技大学 军事基础教育学院，湖南 长沙410073 2、国防科技大学 文理学院，湖南 长沙410073）

自20 世纪40 年代以来，微波科学技术在生物医学、通信、国防军事等领域都表现出巨大的应用价值。例如，1939 年至1945 年的雷达诞生及成熟、1946 年至1971 年的天文学大发展、1944 年至今的微波波谱学及量子电子学大进步、1947 年至今的微波医学应用、1964 年至今的卫星通信广播建立和普及等等，都离不开微波科学与技术的贡献[1]。

作为电磁波谱中的一个特定频段，与人们熟知的可见光频段相比，微波的频率较低（300-300000MHz）、波长较长（1-1000mm）[2]。微波具有基本的波动特性，服从经典的麦克斯韦方程组，在传播过程中会表现出与可见光类似的反射、折射、透射、干涉、衍射等现象。深入研究微波的这些基本特性及其规律，有助于更好地发挥微波的特点并加以利用。因此，国内许多高校在物理实践课程中开设了微波分光及相关实验，以使学员更好地理解掌握微波物理、微波技术等有关知识。

在微波分光及相关实验中，常常将测量微波波长作为基础性实验内容之一，这是因为微波与物质（物体）的相互作用与波长相关，非常有必要掌握微波波长。基于微波分光计测量微波波长的方法有很多, 包括迈克尔逊干涉法[1]、法布里- 珀罗干涉法[2]、双缝干涉法[3]等等。这些方法各有优缺点，其中，对于微波双缝干涉，在条纹对比度及双缝参数选取方面已有研究[4]。然而，关于双缝干涉法测量微波波长时的准确度及可靠性方面鲜有报道。

鉴于此，本文基于波的双缝干涉原理，以迈克尔逊干涉仪为基础进行改装，采用铝板作为双缝，通过旋转探测器，观察微波在干涉时信号的变化趋势。通过对实验数据的采集分析，实现对微波波长的较高精度的测量。

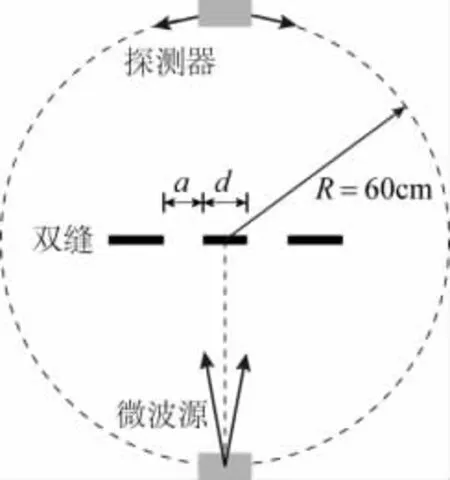
图1 实验装置（俯视）示意图

1 实验装置及主要过程

图2 实验装置图

实验中，首先利用迈克尔逊干涉原理测量微波波长作为参考值。将微波源、探测器、金属反射板和玻璃板按迈克尔逊干涉光路放置。玻璃板使用一块，用于微波分束。金属反射板使用两块，其中一块固定不动，另一块可沿微波传播方向移动。当反射板移动时，探测器信号（检波电流）周期性出现极大、极小值。记录检波电流出现极大、极小值时所对应的金属板移动距离，拟合得到微波波长参考值。

然后搭建双缝干涉装置。取下接收天线，将玻璃板更换为双缝，调整好微波源、双缝、接收器的准直关系，测量有关距离参数。

最后，旋转找到双缝正后方处检波电流极大值位置，记下示数及对应的角度；接着旋转探测器，记下检波电流极大、极小值示数及对应的角度，改变双缝间距后再次测量。

2 微波双缝干涉测量波长原理

本实验的微波双缝干涉虽然原理上与杨氏双缝干涉相同[3]，但不满足条件R>>d，且探测器只能沿圆周运动。因此，必须严格计算波程差，以确定干涉加强条件。

设探测器旋转角为θ，则探测器与双缝的距离R1、R2分别为：

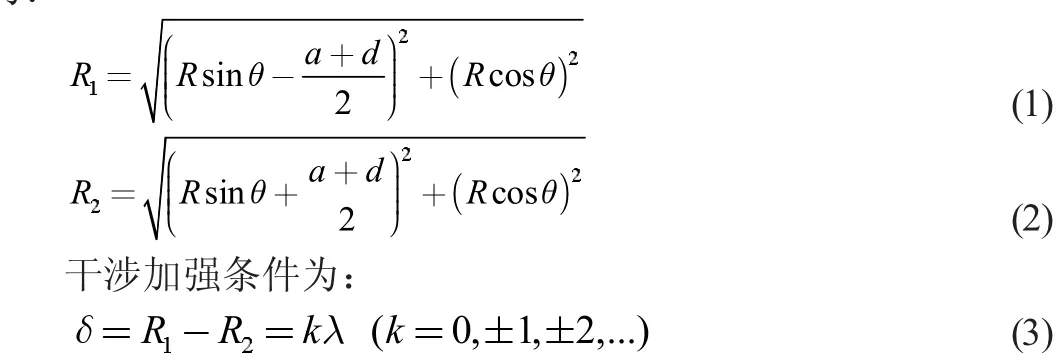
式（3）中δ 为波程差，k 为干涉级次。

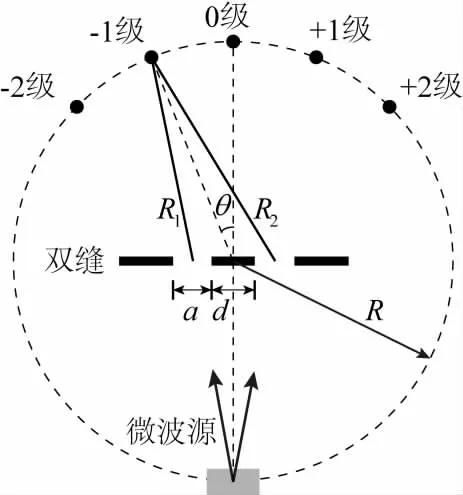
图3 实验原理示意图

3 实验结果及数据分析

首先，对迈克尔逊干涉测量数据进行处理，得到微波波长的参考值λr。迈克尔逊干涉测量数据如表1 所示。

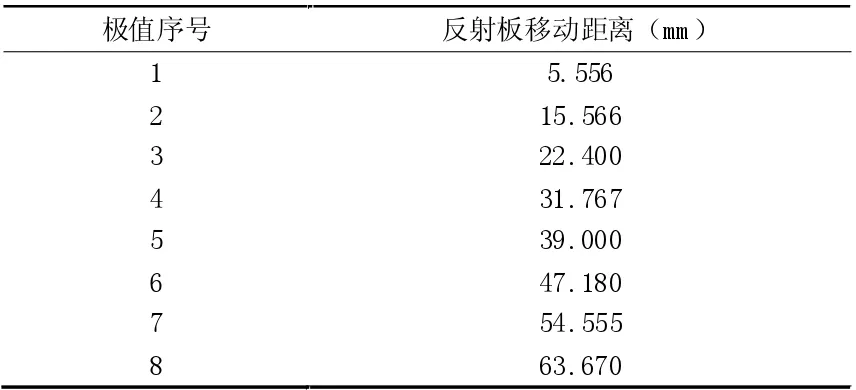
表1 迈克尔逊干涉测量数据

在图4 中，利用最小二乘法对迈克尔逊干涉测量数据进行拟合，所拟合直线的斜率即为λr/4。显然有，λr=4×8.134mm≈3.25cm。

图4 迈克尔逊干涉测量数据及拟合直线

然后，取双缝参数a=4cm、d=4.9cm，记录下的检波电流极值及对应角度数据如表2 所示。为了便于分析，表2 中还列出了根据公式（1）-（3）所计算出的波程差δ、干涉级次k。

由表2 可知，双缝干涉±2 级信号非常弱，而0 级、±1 级信号较强。因此，仅采用位于0°、-20.4°、和21.8°的干涉极大进行计算，得到微波波长λ=3.24cm。与迈克尔逊干涉测量出的参考波长λr相比，仅存在0.31%的偏差。

最后，取双缝参数a=4cm、d=13cm，并装好接收喇叭，记录数据如表3 所示。为了便于分析，表3 也给出了波程差δ、干涉级次k。

表2 双缝干涉实验数据（a=4cm、d=4.9cm）

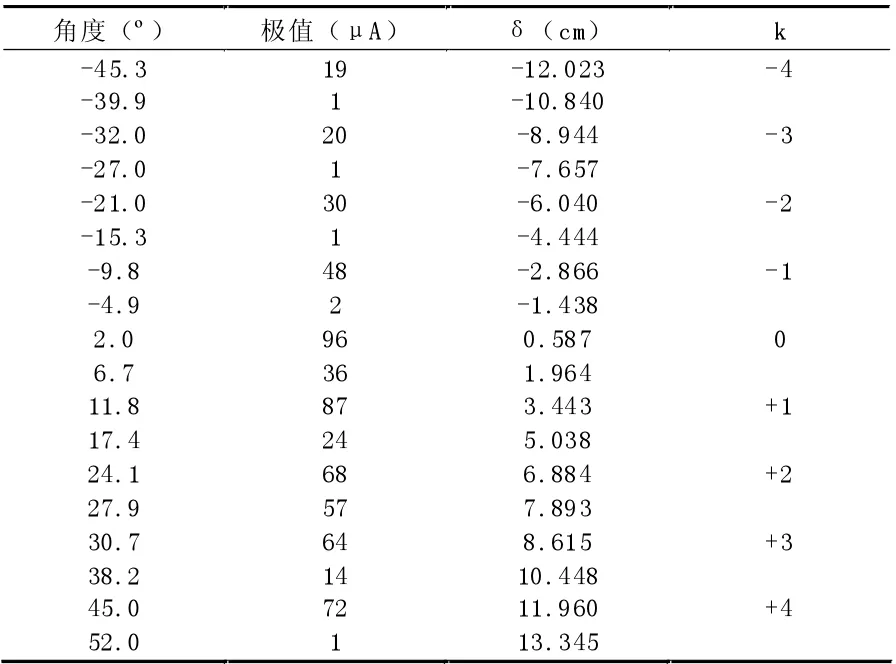
表3 双缝干涉实验数据（a=4cm、d=13cm）

由表3 可知，这种条件下双缝干涉各级极大的信号均较强，这是因为安装了接收天线。若使用0 级、±1 级干涉极大对应的数据进行计算，得到微波波长λ1=3.15cm，与参考波长λr的偏差为3.08%；若使用0 级、±1 级、±2 级干涉极大对应的数据进行计算，得到微波波长λ2=3.22cm，与参考波长λr的偏差为0.92%。

由上述实验结果可知，与加装接收天线相比，不安装接收天线时虽然信号较弱，但波长测量准确度更高。另外，当探测角较大时，存在理论预测之外的其他峰，且信号强度趋于不对称分布，对波长的计算造成明显影响。

4 结论

本文针对双缝干涉法微波波长测量开展了实验研究。结果表明，与加装接收天线相比，不安装接收天线时虽然信号强度较小，但波长测量更准确。实验发现探测角较大时存在无法消除的反常峰值，对波长测量产生一定影响。本文研究有助于弄清双缝干涉法测量微波波长的误差来源，为相关实验内容的开设和拓展提供参考。