基于Levenberg-Marquardt算法的串联协作机器人精度标定研究
李 杨,金小飞,刘国锋,吴明明
(1.安徽三联学院 机械工程学院,安徽 合肥 230000;2.哈工大机器人(合肥)国际创新研究院,安徽 合肥 230000)
随着科技的发展,针对机器人的程序化和思维单一的特点,在工作过程中会出现一定的偏差,因此机器人研究人员制定一系列的串联协作机器人精度标定方法来制约机器人的行为[1-2]。
机器人的行为精度是评估机器人性能的重要指标之一,串联协作机器人在完成一项任务中需要两个或者两个以上的机器人共同完成,因此对于机器人的行为精度要求更加严格,一旦任意一个机器人出现错误操作,就会使任务执行失败。所以研究人员通过串联协作机器人精度标定方法制约机器人的行为,将最大程度地保证机器人行为的准确度,传统的机器人精度标定方法没有考虑到机器人行为判定的误差,对机器人行为制约时,不能达到预期的效率[3]。
综上所述,本文将研究基于Levenberg-Marquardt算法的串联协作机器人精度标定方法,解决以上问题。本文通过分析机器人精度标定的原理,突破传统思维,调用Levenberg-Marquardt算法制定一套全新的机器人行为控制模型,完成基于Levenberg-Marquardt算法的串联协作机器人精度标定方法的研究。
1 串联协作机器人精度标定行为分析
目前标定方法主要包括多点标定法和外部基准标定法,外部基准法必须有一个准确的参照物才可以完成标定任务,多点标定方法不需要外接参照物辅助,所以对于机器人精度标定行为,本文采用多点标定法辅助完成。多变标定方法的原理是将机器人有效识别的环境转化为一个以X轴为原点的三维坐标系,然后通过数据建模测量需要标定的数据变量、标定涉及到的方位等其他相关数据,最后通过机器人精度标定行为模型规划出机器人标定的具体行为,完成机器人的精度标定操作[4]。建立的三维直角坐标系如图1所示。

图1 三维直角坐标系
多点标定方法完成一个任务时最少在一个环境内以5种姿态使机器人的探针接触到标定板上的孔位,标定板越大,接触的次数越多,才可以保证机器人标定的精度。整个标定过程机器人的探头的位置不变,接触是通过机器人的关节转换不同角度完成的。测量数据的准确度决定了标定方法的精度,在标定过程中,三维坐标系中的方位角确定标定空间的位置和机器人所属的空间姿态位置,机器人在完成标定过程中要时刻保证坐标系的基座位置不发生变化,一旦变化标定结果无效。多变标定方法的标定过程简单,并且成本低,被应用于多个领域[5-6]。
1.2 串联协作机器人精度标定行为建模
串联协作机器人精度标定行为模型主要是将机器人的行为通过三维坐标系的形式展现出来,一方面可以在坐标系中根据指令模拟机器人的标杆行为,另一方面模型可以保证多个机器人协作的连续性,保证机器人标定行为的精度[7]。每个连杆的变换坐标的齐次变换矩阵如式(1)所示。
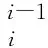
(1)
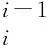
图2 协作机器人标杆
协作机器人的多个标杆共同运动构成一个完成的运动行为,因此将每个机器人向外发射的标杆行为进行变换合成,就形成一个行为标定模型,具体公式如式(2)所示。
(2)
其中,βi表示机器人标杆运动的实际角度。
建立串联协作机器人精度标定行为的运动模型后,为了提高机器人的行为标定精度,本文在串联协作机器人精度标定行为运动模型的基础增加一个MHD误差模型,用来校正机器人的运动精度。MHD误差模型的核心是将机器人的运动行为作为一个转动项,然后将动作所涉及到的机器人末端关节分别进行修正,最后将机器人的执行指令和行为之间的误差降到最低,保证机器人运行的标定精度[8-9]。标定过程如图3所示。
图3 标定过程
本文设定机器人转动项的形式为Rot(y,b),传统的机器人末端行为标定指令思维矩阵如式(3)所示。
(3)
加入转动项后机器人精度行为标定误差矩阵如式(4)所示。
Δp=NaΔa+NcΔc+NdΔd+NθΔθ+NβΔβ
(4)
其中,Na表示连杆长度的误差所对应的系数矩阵;Nc表示连杆转角a的误差所对应的系数矩阵;Nd表示连杆偏距d的误差所对应的系数矩阵;Nθ表示关节角θ的误差所对应的系数矩阵;Nβ表示绕y轴旋转角β所对应的误差的系数矩阵;Δa表示连杆长度误差;Δc表示连杆转角误差;Δd表示连杆偏距误差;Δθ表示关节转角误差[10]。
当给机器人下达一个合作任务后,首先每个机器人根据植入的串联协作机器人精度标定方法进行思维规划,计算出目前机器人所在位置的坐标,然后按照行为标定误差矩阵计算出实际的位置坐标,则最终的机器人运动精度标定误差模型如式(5)所示。
(5)

机器人运行内部结构如图4所示。

图4 机器人运行内部结构
2 基于Levenberg-Marquardt算法的串联协作机器人精度标定研究
Levenberg-Marquardt算法是一种通过非线性最小二乘法寻找可以使函数或者模型最小化的参数向量优化算法,被广泛地应用于多个领域,对于本文研究的串联协作机器人精度标定方法,优势是将机器人行为标定模型结果进行优化,得出最简洁的行为模型,提高机器人行为标定的精度。
Levenberg-Marquardt算法首先是要对模型中的每个未知参数进行偏导计算,进而计算出每个标杆行为之前的迭算步长,然后对步长赋予信赖修正的权限,使得算法对串联机器人精度标定模型的标杆矩阵完成优化。
最后进行迭代结算,将多个机器人传送的连杆矩阵按照步长进行迭代计算,计算公式如式(6)所示。
(6)
其中,rk是用来决定步长dk以及调整迭代过程中因子xk的大小,如果rk越接近1,说明模型函数与机器人行为标定的目标函数误差越小,则可以减小xk的数值使得下一次的试探步dk+1更长;反之rk越小,可以减少dk或者不变,增大xk数值,使串联协作机器人精度标定的原则不发生改变[13-14]。
通过以上对串联协作机器人行为精度标定模型、MHD误差模型以及Levenberg-Marquardt算法的分析,本文总结基于Levenberg-Marquardt算法的串联机器人精度标定方法的工作流程,具体步骤如图5所示。

图5 基于Levenberg-Marquardt算法的串联协作机器人精度标定流程
根据图5所示的串联协作机器人精度标定流程可知,机器人若是未接收到命令,仅需等待即可,若是机器人接收到命令,则需完成下述具体内容:
首先,每个机器人根据自己所在的位置选择需要完成任务的分任务,然后机器人以自身作为坐标原点,将任务指令带入构建的串联协作机器人精度标定模型中,以实现数据采集为目的,每个机器人将规划出标杆移动的路线;
其次,控制机器人的信号接收器与标定板的相位孔接触次数,即获取控制次数,同时机器人将关节每次运动的数据记录下来;
最后,将机器人运动的数据通过MHD误差模型完成归一计算,剔除初次机器人标定的误差,为二次标定奠定数据基础。剔除误差后重复(2)的操作,最终完成串联协作机器人精度标定操作[15]。
在完成串联协作机器人精度标定操作后,将接收到的停止命令作为精度标定结束的标志。
3 实验分析
3.1 实验方案设计
为了验证基于Levenberg-Marquardt算法的串联协作机器人精度标定的效果,本文通过对比试验进行验证说明,对比试验的方法是基于信号传感的串联协作机器人精度标定方法。实验环境如图6所示。

图6 实验环境
实验参数如表1所示。

表1 实验参数
因为人工记录试验数据会出现误差,所以本文试验的两个机器人分别连接两台计算机,记录试验数据。实验前将两个相同型号的机器人的运动参数设置为相同的默认值,并且分别放在两个模拟的形态环境内,保证试验的科学性和公平性。同一时间工作人员向两个机器人发送标定任务,机器人连接的计算机在试验整个过程中记录时间数据,为试验结果分析奠定基础,直到两个机器人都提交标定结果后,结束试验,对两个机器人标定结果进行精度检验,得出试验结果。
3.2 实验结果分析
得到的机器人误差实验结果如图7所示。
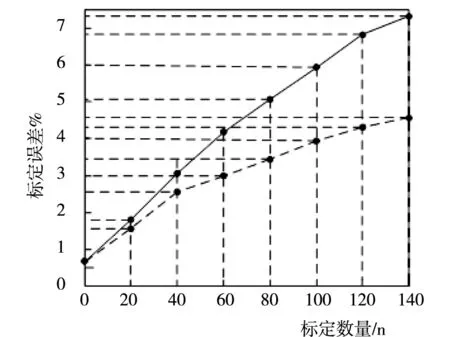
图7 机器人标定误差实验结果
经过以上试验操作,试验结果表明本文研究的基于Levenberg-Marquardt算法的串联协作机器人精度标定方法比传统的精度标定方法的标定精度高,并且机器人完成标定的时间短,具有较高的工作效率。得到这一结果的主要原因是基于Levenberg-Marquardt算法的串联协作机器人精度标定方法融合了MHD误差模型,在机器人标定行为执行前,误差模型对照实时的工作环境与标定任务,对机器人规划的行为进行误差检测,使得机器人模拟标定运动行为时的误差率最低,提高串联协作机器人标定的精度。传统基于信号传感的串联协作机器人精度标定方法通过位置信号确定标定的位置,但是在实际工作过程中外界会出现一定的信号干扰,降低了机器人标定的精度。另外基于Levenberg-Marquardt算法的串联协作机器人精度标定方法对比传统的方法采用二次标定模式,有效的将第一次标定结果中存在的不足,经过第二次标定操作进行弥补。采用两次标定模式并没有降低串联机器人精度标定方法的工作效率,因为此标定方法每个流程对于传统的标定流程来说都是最简洁的,并且流程之间具有较好的衔接性,从而提高机器人标定流程的顺畅性,保证标定效率。
综上所述,基于Levenberg-Marquardt算法的串联协作机器人精度标定方法可以提高机器人标定结果的精度,具有应用意义。
结语
基于Levenberg-Marquardt算法的串联协作机器人精度标定方法在传统的串联协作机器人精度方法的基础上增加了对机器人行为精度误差的权衡,并且调用Levenberg-Marquardt算法对机器人每个行为进行收敛计算,提高协作机器人行为的精度,使机器人工作失误率达到最低。最后通过试验分析证明本文研究的机器人精度标定方法对机器人的行为制约能力,使机器人的行为精度达到百分百,满足投入使用的要求准则,达到研究的预期效果,促进串联协作机器人领域的发展。

