基于全桥荷载试验的预应力混凝土箱梁桥承载力评估

常智慧，乔文庭,2，马鸣谷，哈 图,2

(1.内蒙古自治区交通建设工程质量监督局，内蒙古 呼和浩特 010051；2.长安大学 公路学院，陕西 西安 710000)

随着交通运输事业的蓬勃发展，各种结构形式的公路桥梁不断涌现出来，桥梁的跨径、桥面宽度和结构承载能力在不断增长，桥梁的施工，计算和分析方法也在日趋复杂，某些处于特殊地区的公路桥梁还存在较多耐久性问题。随着交通量的不断增大和桥梁服役年限的增加，桥梁出现了不同程度病害，甚至破坏，这些问题严重影响了公路桥梁的承载能力。因此，在公路桥梁结构服役前，合理的评估其承载能力和可靠度指标十分必要。

全桥荷载试验是通过施加车辆荷载，引起桥梁的振动和变形，从而测得桥梁结构某一关键部位的应力、挠度等变化，为桥梁结构的评价提供参考[1]。目前关于桥梁荷载试验的研究成果较多，田志勇等[2]对自锚式悬索桥进行了荷载试验，分析了桥跨结构在行车激振下的冲击性能；罗国权[3]通过对钢筋混凝土桥梁在4种重型车辆作用下的荷载试验，得到梁跨最大正弯矩、支点负弯矩处断面的抗弯、抗剪及基础承载能力；李勇等[4]以钢筋混凝土T梁旧桥为研究对象，通过常规试验获得结构承载力验算系数，进而评定了服役旧桥的极限承载力。

本文以新建G7高速公路桥梁为依托，对已建成的公路桥梁进行桥梁荷载试验，通过分析试验数据，综合评定桥梁结构的承载能力，为交工验收提供技术依据。

1 工程概况

G7公路为新建北京到新疆高速公路，2017年7月通车，选取其中的一座公路桥进行试验研究。乌兰艾力格2#大桥位于S312附近，桥位轴线呈近东西走向，桥梁为跨越河流而设置，桥位区地貌类型为河漫滩地貌，河谷宽阔，地势平缓。中心桩号为K649+350，起点桩号为K649+297，终点桩号为K649+403，桥梁全长106m，采用5×20m预应力混凝土小箱梁，简支转结构连续，下部结构采用柱式墩、桩基础。单幅桥面宽度为0.5m(防撞墙)+12.75m(行车道)+0.5m(防撞墙)，桥梁设计荷载等级为公路-Ⅰ级，主桥结构示意图如图1所示。

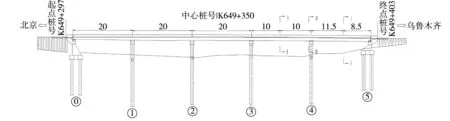
图1 主桥结构示意图(单位：m)

2 荷载试验设计及原理

2.1 有限元模型

采用土木工程通用有限元分析软件Midas Civil对桥梁进行模型计算，有限元模型如图2所示。

图2 梁格法有限元模型

2.2 加载效率及工况

本次荷载试验为交工验收荷载试验，以设计荷载作为控制荷载，静力检测荷载(活载部分)效率η按下式取值。

(1)

0.85≤μ≤1.05

(2)

式中η表示设计取用的冲击系数；Ss表示检测荷载作用下，控制截面变形或内力的计算值；S表示设计标准活载荷载作用下，控制截面变形或内力的计算值(不计冲击系数)。

静载检测采用等效荷载控制加载。本次检测所选取的η值均满足上述要求，检测荷载所产生的力学效应能够满足对梁的力学性能检验和分析要求。

加载工况的确定主要依据以下原则进行。

(1)在满足荷载效率及试验目的前提下，加载工况进行合并、简化，以减少加载位置，同时兼顾其他截面不产生超过其最不利荷载效应的情况；

(2)每一加载工况依据某一加载试验项目为主，兼顾其他加载试验项目。

通过模型计算，静载试验各工况荷载效率如表1所示。

表1 各工况荷载效率

说明：表中理论值均为设计偏载效应作用下边梁理论计算值；表中试验值均为试验偏载效应作用下边梁试验计算值。

3 桥梁静载试验分析

静载试验通过施加静荷载，检验结构主要受力部位在最大(最小)内力下的应力和变形[5-6]。本桥为左右幅分离5跨连续箱梁桥，以左幅试验进行分析，右幅加载情况相同。静载试验采用UCAM-60B静态速采仪采集静载过程中桥梁的静态应变及挠度变化情况，试验加载车辆采用总质量50t的三轴车进行加载，布载形式依据控制截面内力影响线来确定，并满足荷载效率要求。

3.1 加载方案及测点布置

为了满足桥梁承载力设计评定要求，在选择测点布置截面时，应根据桥梁结构的内力包络图，选择最不利受力位置。加载过程分三个等级，静载正式开始前先进行预压，保证应变片及位移传感器接触良好，然后按照预先设计好的加载方式开始正式加载，对于工况I、II，第一级加载为一辆车然后每级增加一辆车；而工况Ⅲ，第一级和第二级各一辆车；第三级增加两辆车，全部加载完成待数值稳定后进行读数，并按加载的反向进行卸载。各工况车辆加载示意图如图3所示。

(a)工况I加载车辆布置图 (b)工况II加载车辆 (c)工况Ⅲ加载车辆布置图图3 设计车辆荷载布置图(单位：mm)

为综合评定桥梁的承载能力，对工况I、II采用跨中截面偏载加载方式，选取跨中截面作为应力、应变及挠度的测试截面，断面测点布置如图4所示；对于工况Ⅲ(4#墩顶最大负弯矩)，测试加载过程中应力应变变化情况，断面测点布置如图5所示。

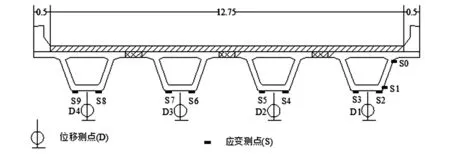
图4 工况I、II横断面测点布置图(单位：m)

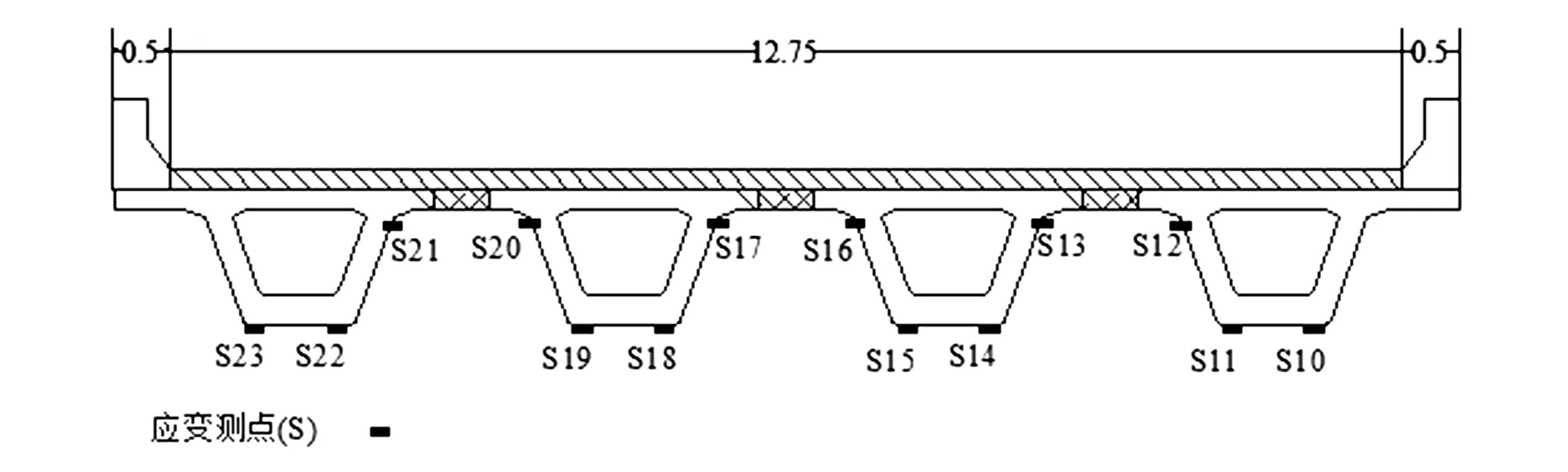
图5 工况Ⅲ横断面测点布置图(单位：m)

3.2 静载试验结果分析

3.2.1 挠度测试结果

挠度是反映承重结构整体状态的重要指标，静载试验得到三级加载下工况I、II跨中截面各测点的挠度实测值，并与有限元计算值进行对比分析，其结果如表2、表3所示。由表2分析结果可以看出，在对边跨主梁最大正弯矩加载过程中，跨中截面挠度实测值均小于计算值，校验系数在0.44～0.49之间。

表2 工况I挠度测试结果

由表3分析结果可以看出，在对次边跨主梁最大正弯矩加载过程中，跨中截面挠度实测也小于计算值，校验系数在0.50～0.53之间。

表3 工况II挠度测试结果

对各工况残余值进行分析，发现主要控制测点挠度相对残余挠度值在-0.01～-0.12范围内，相对残余最大为5%，说明桥梁弹性恢复能力较强，图6和图7反映了控制截面实测值与计算值的关系，分析可知实测值与计算值线性关系较好，相关度均在0.95以上，表明结构处于弹性状态，满足设计要求。

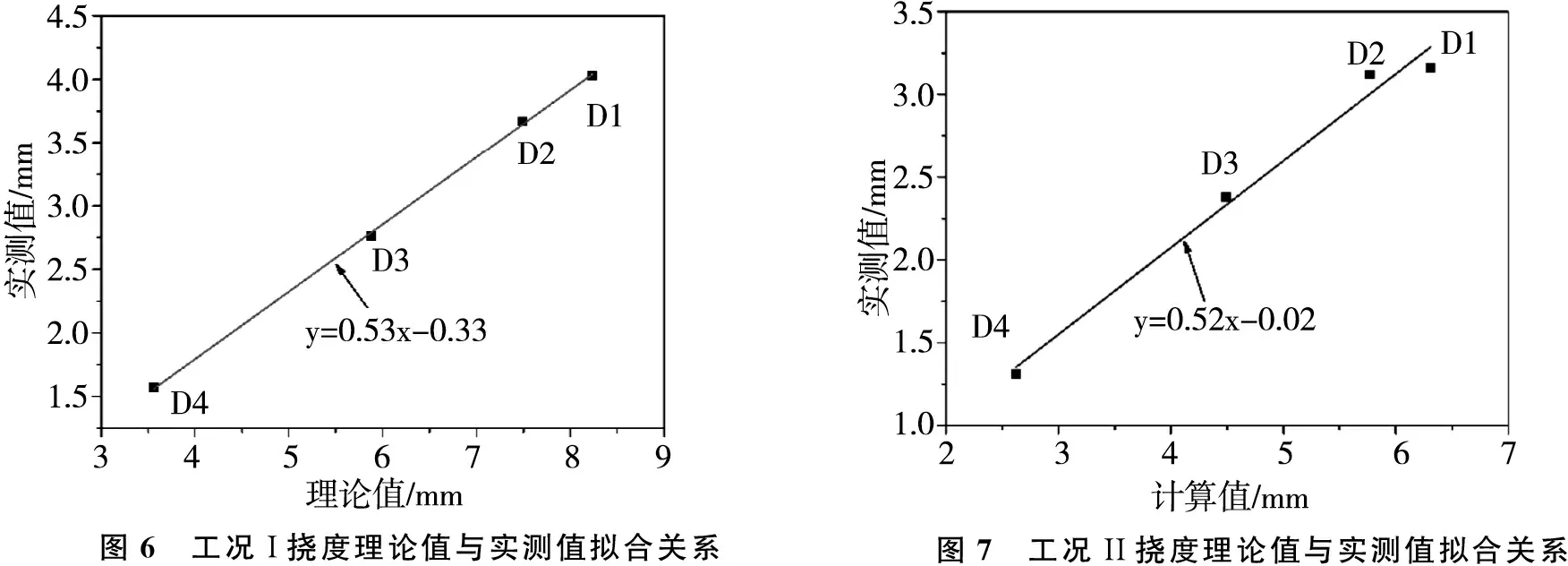
图6 工况I挠度理论值与实测值拟合关系图7 工况II挠度理论值与实测值拟合关系

3.2.2 应力测试结果

表4和表5为公路桥箱梁结构在静载作用下的应力分析结果，通过对应变计算得出各梁静载作用下的应力值。对于工况I(边跨最大正弯矩)，测点应力校验系数在0.51～0.64之间，实测值小于计算值，相对残余不大于6%；对于工况II(次边跨最大正弯矩)，测点应力校验系数在0.47～0.77之间，实测值小于计算值，相对残余不大于6%；说明桥梁在静荷载作用下弹性变形能力较好。

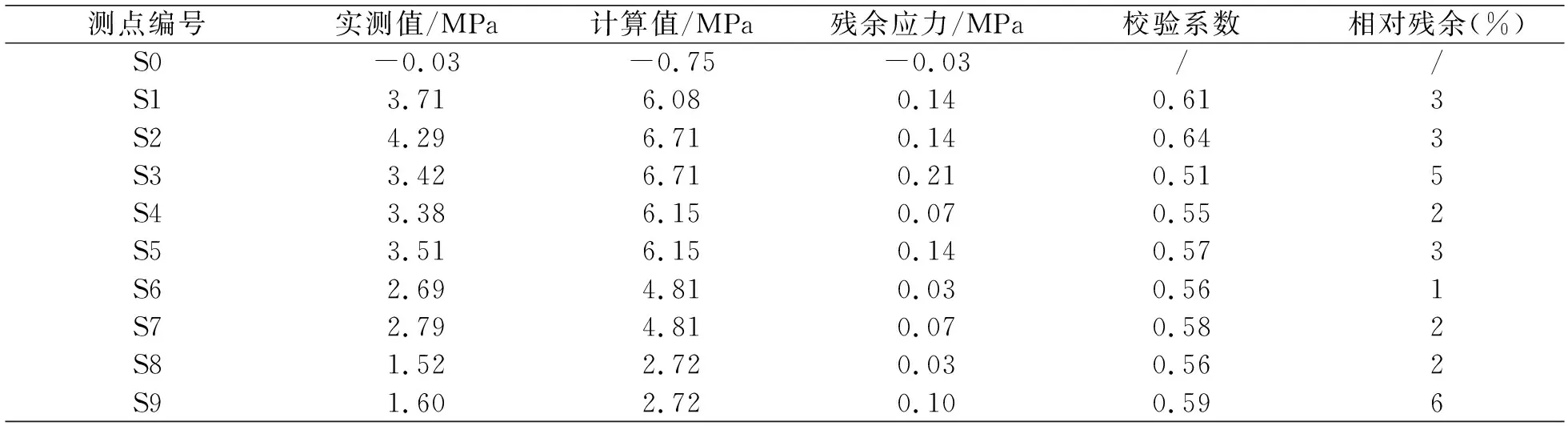
表4 工况I应力测试结果

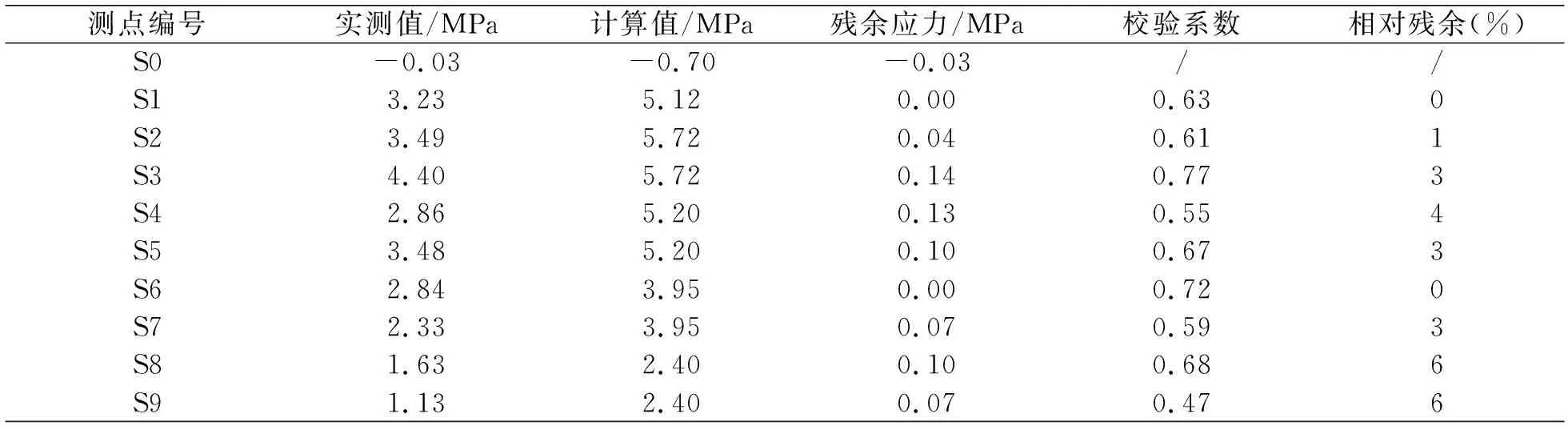
表5 工况II应力测试结果

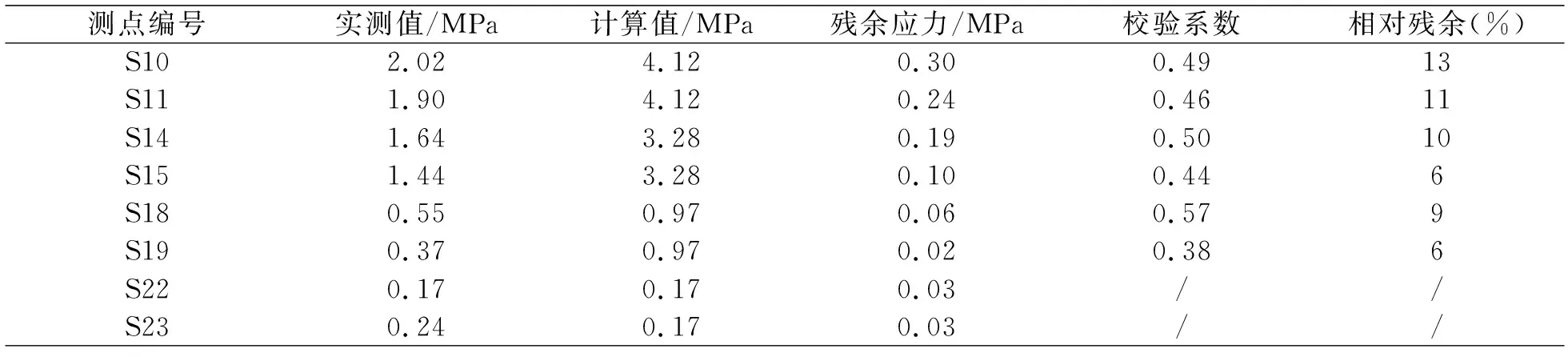
表6 工况III应力测试结果

对于工况Ⅲ(4#墩顶最大负弯矩)，在车辆静载作用下，腹板上部产生的压应变很小，进而计算得到的应力较小，故只分析墩顶梁底应力，表6给出了加载过程中箱梁底部应力的对应数据，对于1号梁应力实测值略大于计算值，但都小于0.35MPa，其余梁实测值均小于计算值，测点应力校验系数在0.38～0.57之间，相对残余不大于13%。

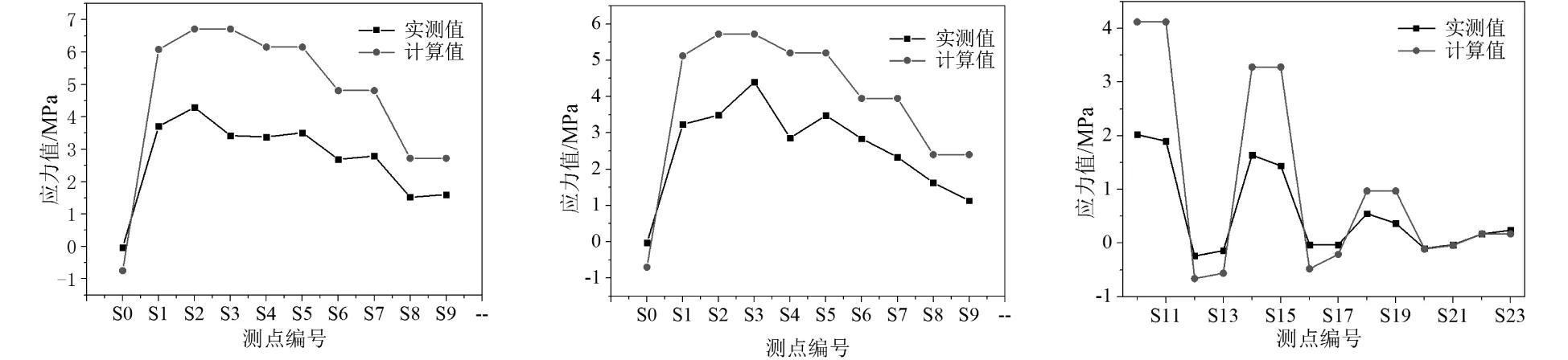
(a)工况I应力变化趋势曲线 (b)工况II应力变化趋势曲线 (c)工况III应力变化趋势曲线图8 各工况应力变化趋势曲线

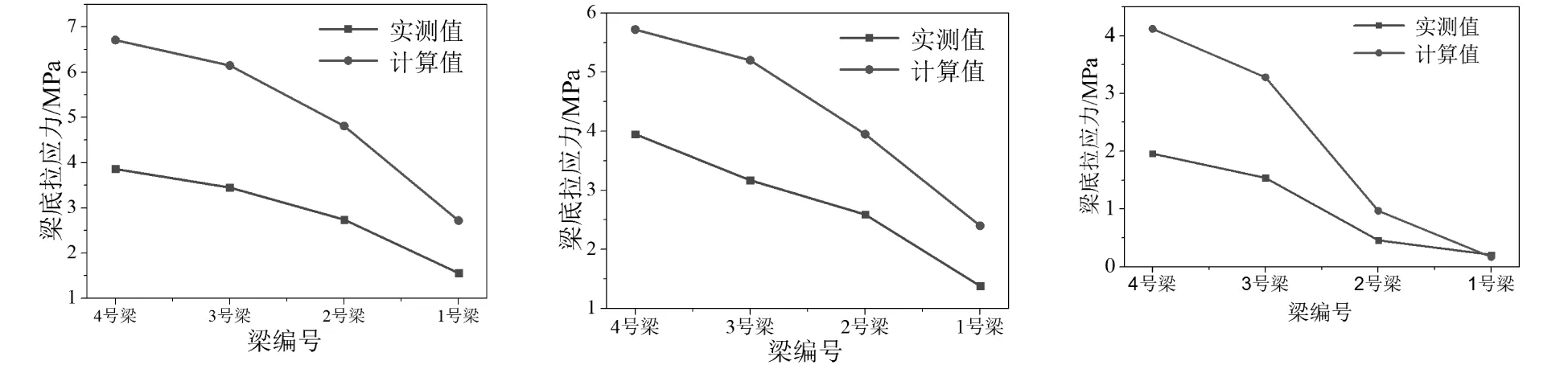
(a)工况I梁底应力变化曲线 (b)工况II梁底应力变化曲线 (c)工况III梁底应力变化曲线图9 各工况下梁底应力变化趋势曲线

图8为工况I、II、III各截面测点应力变化趋势曲线，从图上可以看出：应力实测值与计算值变化规律一致，且实测值均小于计算值，表明桥梁各梁连接工作性能良好，结构强度具有一定的富余。将同一箱梁底部测得的两个应力值取平均数，得到梁底应力变化趋势，如图9所示。图9表明，偏载作用下4号梁应力值最大，依次呈下降趋势。

4 桥梁动载试验分析

桥梁结构的动力性能主要包括：振型、阻尼系数、固有频率等，是反映结构振动的基本特性，结构的动力特性只与结构本身的固有性质有关，如材料性质、支撑情况、结构刚度等，与荷载无关。动载试验是利用某种激振方式引起桥梁结构的振动，进而测定结构某截面的动力响应，不仅反映了桥梁结构在动荷载作用下的受力状态，还反映了动载作用下行车的舒适性。结构在服役期间一旦有较大损失，其动力参数将会产生大的变化[7]，本次动载包括无障碍行车试验和脉动试验。

4.1 模态试验及结果分析

根据桥梁脉动试验原理测试竖向平面内弯曲自振特性[8-9]，当桥面无动荷载以及附近无规则振动的条件下，采用高灵敏拾振器测试系统得到桥梁结构的自振频率、振型和阻尼比如表7所示，并与有限元软件的到的计算值进行比较，竖向一阶振型图如图10所示。

表7 脉动测试结果

由表7可以看出：该桥竖向一阶振型特征频率为6.90Hz，阻尼比为0.689，而该桥振型模型计算频率为5.64Hz，说明结构整体刚度较好，满足设计要求；实测阻尼比较小，表明桥梁整体工作性能良好，具有一定的耗能能力。

图10 竖向一阶振型示意图

4.2 无障碍行车试验及结果分析

在无任何障碍的条件下，载重车(总重500kN)分别以30km/h、40km/h、50km/h、60km/h的速度行驶过桥梁结构，测定桥梁在运行车辆作用下的动力反应。通过测量桥梁结构在动载作用下的动挠度，并分析得出桥跨结构的冲击系数，行车试验测试截面选取边跨和次边跨的跨中截面，取二者平均值作为最终的冲击系数，并与设计值进行比较，结果如表8所示。由表可知，实测冲击系数介于1.04～1.14之间，均小于计算得到的冲击系数值1.32。

表8 跨中截面冲击系数

5 结论

通过对该桥的有限元分析计算以及现场试验比较可以得到以下结论。

(1)静载试验荷载效率为1.02～1.04之间，满足《公路桥梁荷载试验规程》(JTG TJ21-01-2015)的要求，同时试验荷载表明所产生的最不利效应可反映设计规范可变荷载效应的特征。

(2)桥梁主梁控制截面挠度实测值小于计算值，校验系数在0.44～0.54之间，表明主梁结构竖向刚度满是设计要求，卸载后最大相对残余变形为5%，说明主梁结构弹性恢复能力较好，无不可恢复变形。

(3)桥梁实测应力校验系数在0.38～0.77之间，表明主梁各控制截面静力受力性能满足承载力要求，各工况卸载后相对残余较小，表明结构在静载作业下处于弹性工作状态。

(4)动力测试结果显示，实测竖向一阶频率6.90Hz大于计算频率5.64Hz，冲击系数范围为1.02～1.20，均小于计算值1.32，表明结构竖向动刚度良好。