基于张量算法的MIMO雷达多目标角度估计∗

（中国人民解放军91913部队 大连 116041）

1 引言

目前军事雷达应用中对隐身弱目标的探测需求逐渐凸显，而作为近年雷达领域研究的热点，MI⁃MO雷达由于体制优势，其对隐身目标和弱目标的探测较现有雷达体制有较大优势，其符合军事装备发展需求。通信领域中的多输入多输出技术［1］（Multi Input Multi Output，MIMO）已经得到了广泛应用，其被引入到雷达领域形成MIMO雷达概念［2］。MIMO雷达系统由多个收发天线组成，发射天线发射正交信号，接收天线接收反射自目标的信号并可滤波分离，最终集中联合处理这些分离信号。与相控阵雷达相比，MIMO雷达具有波形分集和空间分集效应，可以显著提高目标空间分辨率。MIMO雷达可分为具有共置天线的集中式MIMO雷达［3～4］和具有广泛分离天线的分布式MIMO雷达［5］。集中式MIMO雷达包括单基地和双基地两种，双基地雷达的发射阵和接收阵布置在两个距离较远的阵地中，收发阵内阵元集中布置，本文主要研究双基地MIMO雷达。

众多算法已经应用于双基地MIMO雷达的目标角度估计研究中［6～7］。这些基于矩阵运算的方法没有考虑MIMO雷达接收信号中特有的高维结构，它们将目标的雷达散射截面（RCS）起伏作为研究中的负面因素。而基于张量［8～10］的典范多因子分解算法（Canonical Polyadic Decomposition，CPD）将一段时间的RCS起伏作为接收信号中的时间结构信息而起到正面作用。因此CPD算法增强了参数估计的性能，由于不需要估计信号子空间，其计算复杂度也较小。本文建立双基地MIMO雷达数据模型，其接收信号符合CPD结构，应用CPD算法可估计出多个目标的角度值。最终的仿真结果表明，基于CPD算法的角度估计性能优于Capon和MUSIC算法。

2 双基地MIMO雷达数据模型

2.1 雷达线阵及信号模型

雷达模型使用均匀线阵，如图1所示，设目标为远场点目标，收发信号为窄带信号。易得线阵信号的方向矩阵为

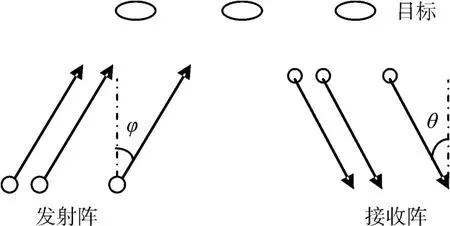
图1 双基地MIMO雷达模型

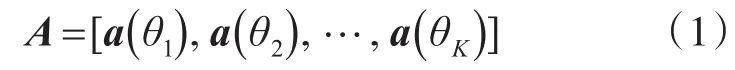
设雷达阵列有M个发射天线，N个接收天线，发射天线发射正交窄带脉冲信号，有相同的中心频率和带宽，脉冲采样点数为L，第m个发射天线发射的信号可表示为sm=[sm(1)，sm(2)，…，sm(L)]T，则发射阵发射的全部信号可表示为

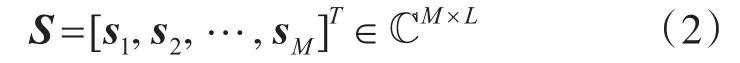
2.2 接收信号模型

由上节线阵信号的方向矩阵可得双基地MI⁃MO雷达的接收阵和发射阵的目标导向矢量分别为

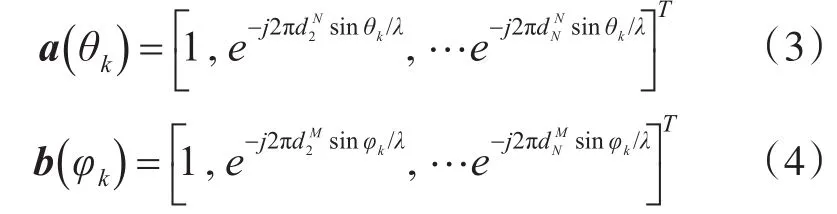
其中φk和θk分别为第k个目标的波离角和波达角，λ=c/f0，为第m个发射阵元与第一阵元的间距，为第n个接收阵元与第一阵元的间距。信号经过多个目标反射后到达接收阵，接收天线接收到的混合信号可以表示为

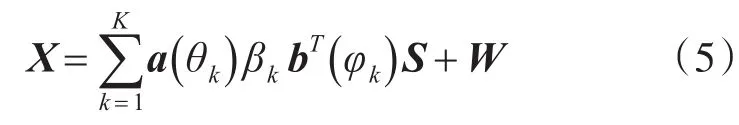
其中βk为第k个目标的RCS系数，在Swerling II信号模型中RCS系数随脉冲变化而变化。W∈CN×L为噪声项。混合信号（5）可写为矩阵形式［11］：

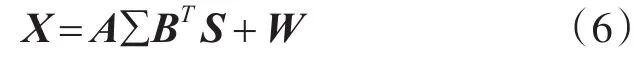
X∈CN×L表示N个接收天线接收的L点采样值的信号，其中c=[β1，β2，…，βK]。

2.3 滤波信号模型

本文建立的双基地MIMO雷达发射信号相互正交，正交信号协方差矩阵(1/L)SSH=IM。则对混合信号进行匹配滤波处理，即在式（6）右乘(1/L)SH后可得

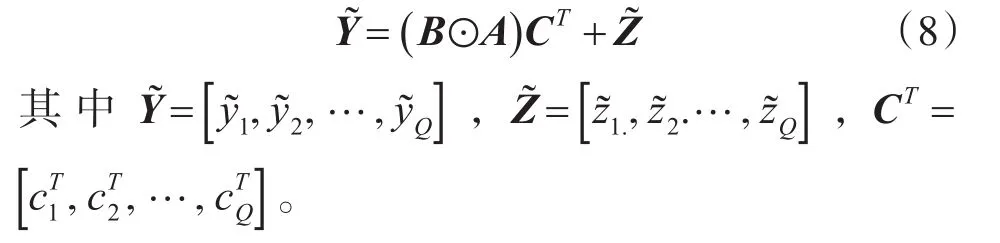
3 目标角度估计的CPD算法

在双基地MIMO雷达的滤波信号数据模型（8）中，A是K个目标的接收阵列的导向矩阵，B是K个目标的发射阵列的导向矩阵，CT包含了K个目标的RCS衰落和多普勒频移的影响。

我们可以利用不同的优化算法［12～13］最小化代价函数来拟合接收信号：

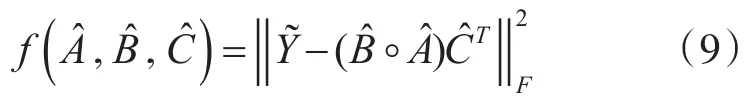
本文主要运用Tensorlab3.0［14］中的CPD函数对接收信号进行CP分解，获得收发阵列的导向矩阵A和B，进而根据A和B的范德蒙结构恢复出AOA和AOD。

4 仿真实验

本节将CPD算法用于双基地MIMO雷达的目标角度估计来做仿真实验。我们选取传统的Ca⁃pon算法和MUSIC算法作为对比算法，以说明CPD算法的优越性。在雷达模型中信号频率为fc=1GHz，波长为λ=c/fc，阵元间距d为半波长，脉冲间隔为5×10-6s。估计误差以真实角度和估计角度的绝对误差为评价标准。

4.1 不同阵元数下目标角度估计

如图2所示，绘制了3种角度估计算法随信噪比变化的角度估计误差曲线。其中目标数K=6，算法误差值为6个目标误差值的平均值，目标的AOD和 AOA 为（ -70°，50°；-65°，45°；-20°，20°；-15°，15°；-10°，10°；5°，-15°），采样点数L=512，脉冲数Q=50，信噪比SNR为-30dB～30dB，每隔5dB进行仿真绘图，循环仿真次数为50次，2D-Capon和2D-MUSIC算法的最小搜索角度间隔为0.01°。从图2可以看出，随着信噪比的改变，在大多数情况下，CPD算法实现的角度估计精度比Capon和MUSIC算法更高，当收发阵元数增加时，CPD算法的角度估计精度亦显著提高。

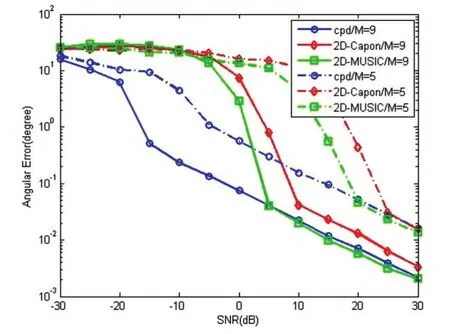
图2 不同阵元数目下角度估计误差对比

4.2 不同目标间隔下目标角度估计

如图3所示，实线绘制的是目标间相隔较远的角度估计误差曲线，虚线绘制的是目标间距离较近的误差曲线。信号采样点数L=512，脉冲数Q=50。当目标间距离较近时，目标的AOD和AOA 为（ -70°，50°；-65°，45°；-20°，20°；-15°，15°；-10°，10°；5°，-15°），当目标间距离较远时，目标的AOD和AOA为（-70°，60°；-50°，25°；-30°，50°；-10°，-20°；10°，0°；30°，30°）。从图中可以看出，目标间相距较远时，三种算法的角度估计误差较小。当目标间距离较近且SNR较低时，基于张量的CPD算法较Capon算法和MUSIC算法拥有更高的目标角度估计精度。

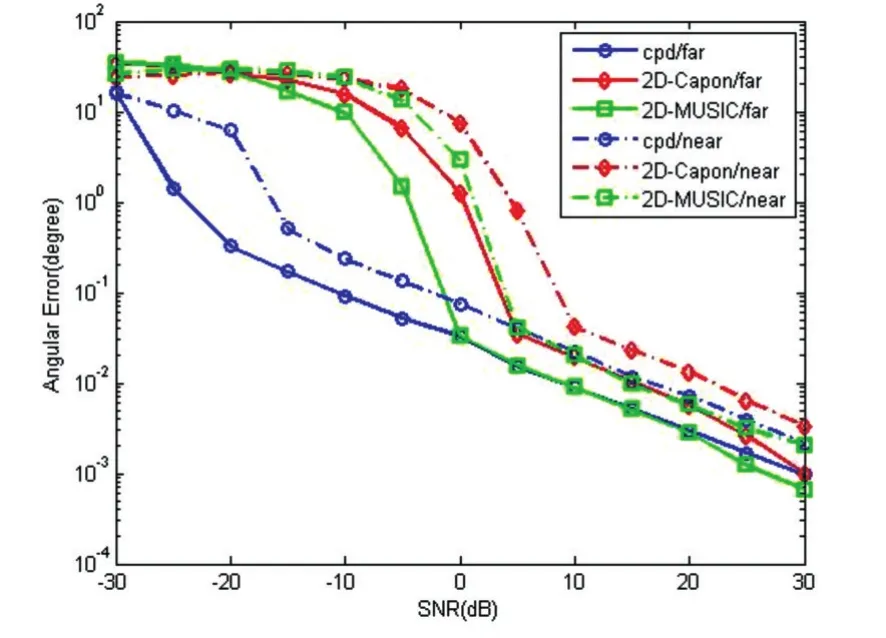
图3 不同目标间隔下角度估计误差对比

5 结语

本文围绕军事雷达装备应用需求，研究了如何将基于张量的CPD算法应用到双基地MIMO雷达的多目标角度估计研究中。构建了双基地MIMO雷达的发射信号模型，正交信号发射至目标后反射至接收阵获得混合信号模型，通过匹配滤波后的信号符合CPD结构。对滤波信号应用CPD算法以估计相关因子矩阵，并提取出多个目标的波离角和波达角。实验结果验证了在双基地MIMO雷达模型中，当目标距离较近和阵元数目较少的情况下，CPD算法较其他算法在目标角度估计精度上均有较大优势，通过增加收发阵元数目可有效提高MI⁃MO雷达的目标角度估计精度。