角点检测精度评估方法研究

童 飞

（上海兴芯微电子科技有限公司，上海 201203）

0 引言

图像处理作为一种高效的信息获取技术，已渗透到社会生活的方方面面。在硬件技术和机器视觉技术的高速发展下，图像处理技术日益融入工业生产之中［1-3］，包括运动跟踪、物体识别和立体匹配等［4-5］。在立体视觉中，棋盘格角点检测是摄像机标定的重要步骤［6］，对标定结果有重要影响［7-8］。

棋盘格角点检测算法从检测方式上分为3 种［9］。第一种是基于图像灰度变化的检测算法，经典的检测方法主要包括Moravec、Harris 和SUSAN 算法。Moravec 算法［10］使用滑动窗口检测局部灰度变化，进而定位边缘和角点，成为后续检测算法的基础。Harris 角点检测算法［1，11-12］根据角点所在区域的灰度变化特性，区别不同类型的点。SU⁃SAN 角点检测算法［13-14］检测角点的相似点数量变化，增加了对噪声的抗干扰性。第二种是基于模板的检测算法，根据棋盘格角点的对称性设计约束，实现对角点的精确检测。Geiger 等［15］设计了关于原点对称的模板，使用图像区域的局部响应检测两种角度的角点；刘飞飞等［16］设计了关于横轴和纵轴对称的环形模板，使用当前区域内的像素跳变次数检测角点；伍明等［17］使用圆形模板来定位候选角点集。第三种是基于轮廓曲线的检测算法。艾裕丰等［18］提出了基于棋盘格边缘的角点检测算法，使用5×5 的窗口定位边缘的法线方向；Zhang 等［4］提出了基于离散曲率的角点检测算法；王晓辉等［19］将基于图像灰度和基于模板的方法结合起来，以提高角点检测准确性。

目前，获取亚像素角点位置的常用算法有双线性插值和二次多项式拟合，根据角点初始位置，通过插值和拟合方式，获得亚像素级别的角点坐标。在标定过程中，精确的角点坐标会提升相机标定精度［20-21］。角点检测作为一个基础技术，对于机器视觉应用非常重要，对角点检测算法评估具有重要意义。

角点检测算法评估［9，22］主要分为5 类：①基于人类视觉评估［23］；②基于理论分析［24］；③基于角点定位精度［25］；④基于标定的参考角点［26］；⑤基于一致性判断［27］。Mi⁃chael 等［23］设计了基于人类视觉的估计方法，邀请计算机视觉专业的9 名学生参与算法效果评估，根据中心物体的辨识度对算法进行排名，参与人员数量、分布和主观喜好会对评估结果产生影响。Rockettt［26］设计了一个成像模型，引入了衍射和采样等物理因素，生成了一组图像集，用来测试角点检测算法性能。本文涉及的物理参数和几何参数，都可以通过标定获得，所得真值数据更加接近于真实的成像过程。Awrangjeb 等［27］提出了一致性判断的评估方法，计算仿射变化前后的角点数量和位置差异，以检测算法稳定性，但该方法无法获取角点的真值坐标，无法定量评估角点位置的检测精度。近年来，立体视觉通过重投影误差定量评估角点检测算法精度［17，28］，该方法排除了人为因素影响，但是受摄像机标定精度影响。骆荣坤等［29］使用Harris 和SUSAN 算法作对比，从漏检、误检和一致性检测3 个角度评估算法性能。

本文提出了一种定量评估角点检测精度的方法，主要包括3 点：首先，通过计算机生成棋盘图像，获取角点坐标位置的真实值；然后，根据相机成像模型，使用真实相机参数，对理想的棋盘格图像进行畸变处理，定位畸变后角点的真值位置；最后，在生成的图像中，使用现有算法检测角点，并将实际检测值与真值进行比较，进而评估算法检测精度。

1 成像模型

1.1 成像模型

本文相机成像模型采用张正友标定模型，通过单应性矩阵建立像素坐标系像点和世界坐标系物点之间的转换关系［1］。本文使用到的基本成像模型如式（1）-式（3）所示。

其中，矩阵M 是相机的内参矩阵；fx、fy是水平和竖直方向的等价焦距，是像素坐标系和物理坐标系之间的转换因子；(u0,v0)是主点坐标。

1.2 畸变模型

镜头成像主要包括3 种类型的畸变：径向畸变、切向畸变和薄棱镜畸变。其中，对于普通相机，径向畸变是最主要的畸变来源［30-31］，且三次方项就可以代表主要畸变量［32-34］。因此，本文畸变模型主要考虑径向畸变，建立畸变模型，如式（4）—式（7）所示。

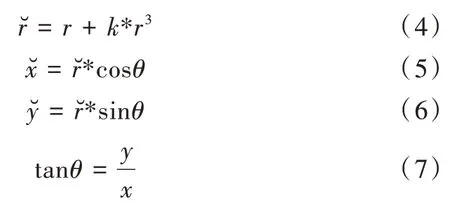
Fig.1 The values of different distortion coefficient K图1 不同畸变系数K 的取值

2 真值计算模型

本文对角点的真值计算过程进行详细描述。首先，通过计算机生成棋盘格图像；然后，根据成像模型，将棋盘格图像从像素域反投影到空间域；最后，根据畸变模型，添加径向畸变，并计算畸变前后棋盘格角点位置。

2.1 反投影模型

通过计算机生成棋盘格图像，记录角点坐标的真值。构建投影和反投影之间的映射模型，从而得到畸变之后角点的真值位置信息。内参的逆矩阵用来构建反投影公式，如式（8）所示。

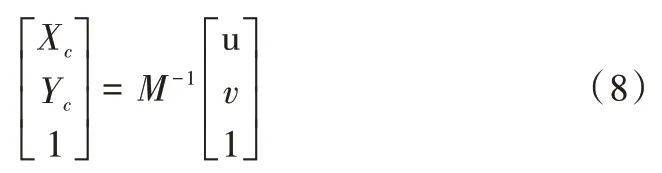
其中，[Xc,Yc,1]T是平面Zc=1 上的点，通过式（4）的畸变模型，建立畸变前后模型如式（9）所示。

通过式（9）计算畸变前的像素坐标。由于角点的真值位置是亚像素级别，本文采用双线性插值算法对其进行恢复。使用角点检测算法对得到的畸变图像进行角点检测，并通过真值评估算法精度。

2.2 算法处理流程

算法步骤如下：①标定得到摄像机的内部参数；②用计算机生成理想的棋盘图像；③使用上述方法计算从畸变像素坐标到理想像素坐标的映射；④利用双线性插值生成畸变图像；⑤利用算法检测畸变图像中的角点；⑥利用式（9）计算畸变像素的真值；⑦使用真值评价角点检测算法精度。

3 实验结果与分析

为了验证评估方法的可靠性，使用不同的角点检测算法和不同的参数对其进行评估。

3.1 评估算法精度

棋盘格角点检测算法主要分为两类：基于角点特征的算法和基于棋盘格特征的算法，前者选取Harris 角点检测算法，后者选取文献［7］的方法。将算法检测结果与真值进行对比，详细结果如图2 所示（彩图扫OSID 码可见）。

实验参数设置如下：棋盘格尺寸为：900*1 200，包括88 个内角点，得到的相机内参如下：fx=1500,fy=1500,u0=600.5,v0=450.5,k=1.5。

Fig.2 Error analysis of corner detection algorithm图2 角点检测算法误差分析

结果显示，两种算法的检测误差关于主点对称。选择棋盘格左上角区域（见图3），对检测结果进行详细分析，详细数据如表1 所示，细节放大效果如图4 所示（选取区域内，红色标记为角点的真值位置，绿色标记为基于棋盘格特征算法的结果，蓝色标记为基于角点特征算法的结果）。其中，Error1 是真值和基于棋盘格特征算法检测结果的绝对误差，Error2 是真值和基于角点特征算法检测结果的绝对误差。

Fig.3 Area selection of checkerboard图3 区域选择

图4 显示，本文提出的方法能够非常精确地定位真值坐标，并据此评估角点检测算法精度。实验结果表明，基于棋盘格特征的角点检测算法，最大检测误差为0.263 像素，平均误差在水平和竖直方向分别是0.067 71 和0.049 42 像素。该算法在竖直方向检测精度表现好于水平方向，两者精度相差0.018 29 像素。基于角点特征的角点检测算法，最大检测误差为1.19 像素，平均误差在水平和竖直方向分别是1.007 88 和1.004 33 像素。该算法在水平和竖直方向的精度非常接近。

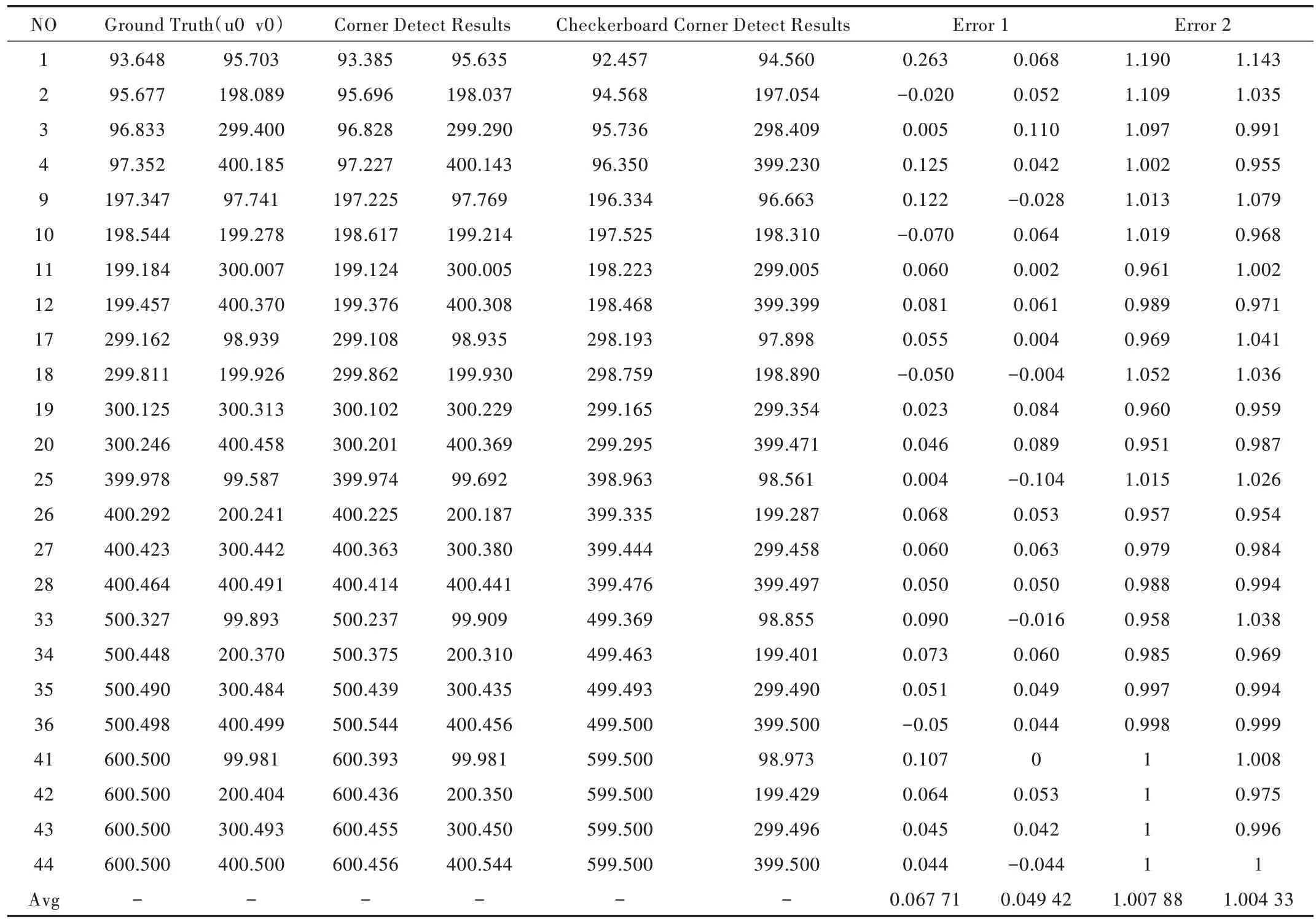
Table 1 The ground truth of corner points in selected area，the coordinates of corner points detected by different algorithms and the detection error表1 选择特定区域角点的真值位置和不同角点检测算法检测的角点位置及绝对误差

3.2 参数影响

畸变系数K 和高斯模糊度是影响图像角点位置的主要因素，选取棋盘格角点检测值进行实验。对这两个变量进行控制实验，计算结果的平均绝对误差（MAE）如表2 所示。

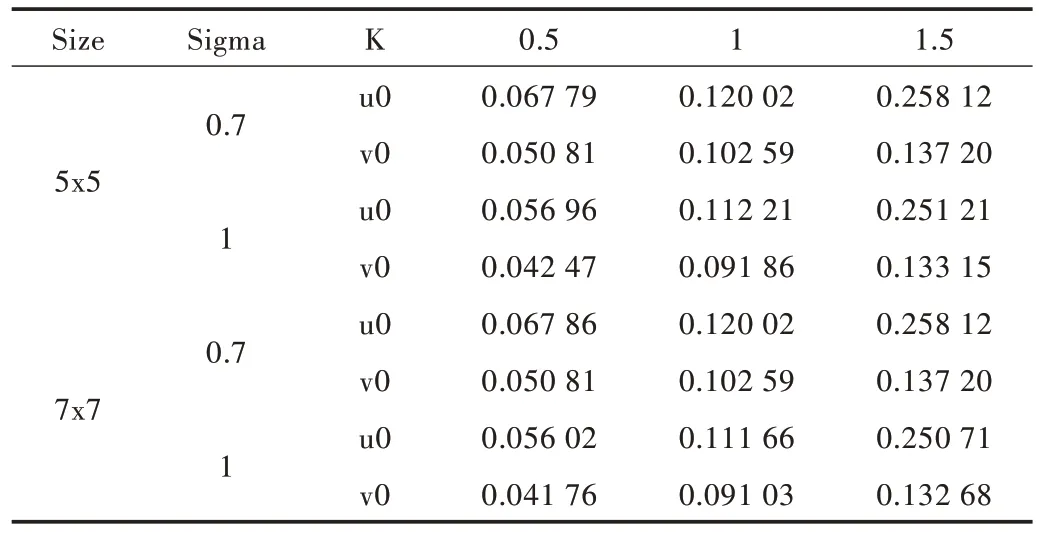
Table 2 Average absolute error表2 平均绝对误差

其中，Size 和Sigma 的值分别是高斯模糊窗口的大小和高斯函数的标准差。当K=0.5 时，MAE 在0.07 像素以下，随着K 的增大，MAE 在0.3 像素以下。当尺寸和Sigma值变化时，MAE 值几乎没有发生变化。因此，本文提出的模型具有较好的鲁棒性。

4 结语

本文方法能够得到角点的真实位置，用以评估角点检测精度。角点检测算法不再局限于主观评估，可以朝着精确性的方向发展。两种角点检测精度结果显示，基于棋盘格特征的角点检测算法具有更高的准确性，在水平和竖直方向的平均误差分别达到0.067 71 和0.049 42 像素。使用不同的原始生成图像，本文方法可以得到多种类型的角点真值。然而，该方法只考虑了径向畸变，后续研究需要加入更完整的畸变模型，增强方法的适应范围。可以从应用角度对角点检测算法进行分类，然后针对不同类型的真值提出相应的解决方案。