一种混合策略改进的灰狼优化算法

倪 静，秦 斌，曾凡龙

（上海理工大学管理学院，上海 200093）

0 引言

灰狼优化算法（Grey Wolf Optimizer，GWO）是Mirjalili等［1］提出的一种群体智能算法。GWO 算法具有结构简单、概念清晰且易实现等特性，已广泛应用于车间调度［2-3］、路径优化［4］、社会网络影响力最大化［5］、参数寻优［6］和聚类优化［7］等问题。尽管GWO 算法得到了广泛应用，但是仍存在一些不足。针对标准GWO 算法的不足，目前国内外学者们主要针对GWO 算法的种群初始化过程、控制参数和搜索机制等几个方面进行改进，进而提高GWO 算法的寻优性能。在种群初始化的优化方面，文献［8］利用佳点集对算法种群进行初始化，保证初始种群个体分布均匀，为算法的全局寻优奠定基础；文献［9］采用高斯分布对种群进行初始化，使得种群分布更加均匀，通过实验验证了该策略可以提高算法求解精度；在控制参数调整方面，文献［10］受粒子群优化算法启发，提出一种非线性递减收敛因子更新公式；文献［11］在基本灰狼优化算法的基础上，通过其动态缩放因子和交叉概率因子提升算法寻优能力；在位置更新改进方面，文献［12］分析了灰狼优化算法后期个体均向决策层区域聚集，从而导致群体多样性较差的问题，并提出一种基于光学透镜成像原理的反向学习策略以避免算法陷入局部最优；文献［13］受差分进化和粒子群优化算法启发，构建一个修改的个体位置更新方程以增强算法探索能力，并提出一种控制参数随机动态调整策略，增强算法全局搜索能力；文献［14］为协调算法的全局探索和局部开发能力，设计了一种基于正切三角函数描述的非线性动态变化控制参数，并给出了一种新的个体位置更新公式，以加快算法收敛速度。此外，将其他智能算法与灰狼算法结合也成为一种新的研究思路，学者们已经将蝙蝠算法［15］、鲸鱼算法［16］和布谷鸟算法［17］等与GWO 结合，以改善算法寻优性能。虽然国内外学者对GWO 算法进行了大量改进研究，但是其初始种群不均匀、全局勘探与局部开发能力不平衡和易陷入局部最优等问题依然存在。

本文在已有研究基础上提出了一种多策略改进的灰狼优化算法（Improved Grey Wolf Optimization Algorithm，IG⁃WO），采用反向学习策略产生了更加均匀的初始种群，改进传统灰狼优化算法在初始化过程中种群不均匀的问题。针对算法全局勘探与局部开发能力不平衡问题，采用非线性控制因子平衡算法全局搜索能力和局部搜索能力。为进一步提高算法全局搜索能力，在位置更新策略中引入莱维飞行策略，扩大搜索范围。通过12 个标准测试函数仿真验证改进算法的准确性和有效性，仿真结果表明，本文改进的算法具有良好的收敛精度、速度和稳定性。

1 混合策略改进的灰狼优化算法

1.1 基于反向学习策略初始化种群

标准的GWO 算法是基于随机性产生的初始种群，这可能使得算法的初始种群分布不均匀，难以保证种群的多样性。而算法的初始解对算法全局搜索起到了至关重要的作用，种群的多样性程度也极大地影响着算法搜索性能。文献［18］表明，反向解有50%的可能性比当前解更加靠近最优解，因此，本文采用反向学习策略产生初始种群。

首先，在解空间内对种群进行随机初始化，产生一组随机种群，种群内的每个个体xi,j，i∈[1,D]代表维度，j∈[1,n]代表种群个数。然后，对每个个体采用反向学习策略，即采用式（8）找到反向个体构造一组反向解，最后将两组初始解合并，选取适应度前n的个体作为初始种群。

1.2 控制参数的非线性调整策略

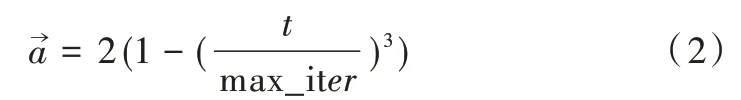
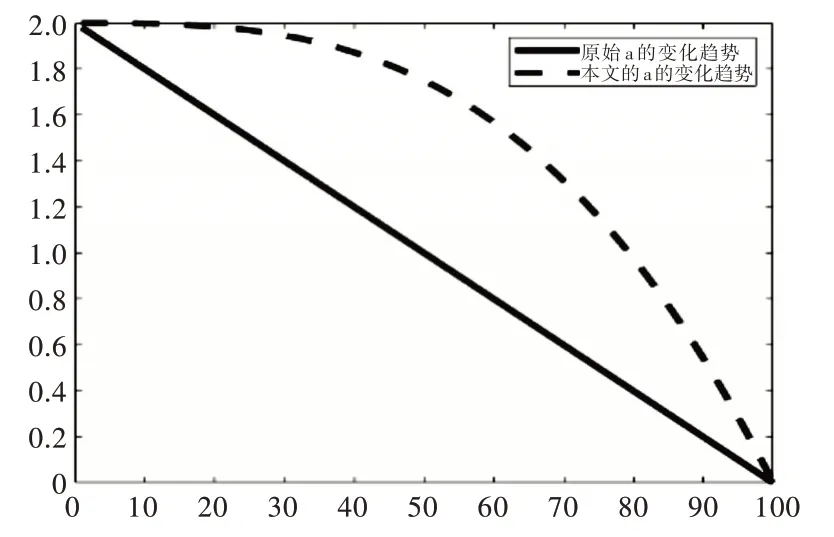
Fig.1 Convergence curve of parameters图1 参数对比曲线

1.3 位置更新策略改进

在标准GWO 算法中，只有α狼、β狼和δ狼的位置影响下一代位置，下一代种群过度向全局最优“靠拢”，很容易出现局部寻优。为了进一步增强算法的全局搜索能力并加快收敛速度，在原始位置更新策略基础上引入莱维飞行策略。莱维飞行是一种随机游动的搜索策略，能够扩大搜索范围，防止算法陷入局部寻优。引入莱维飞行的位置更新策略如下：

其中，⊕为点对点乘法，a0=0.01，sign[rand-1/2]的取值为-1，0 和1。莱维飞行的步长服从莱维分布：

其中，s是飞行路径，可由Mantega 算法计算如下：

θ的取值范围一般为（1，2），本文取值1.5，μ和u是符合正态分布的随机数：u～N

1.4 算法流程

将增加以上改进策略的灰狼优化算法简写为IGWO，算法流程描述如下：

Step1：设置算法参数，包括种群数目n，最大迭代次数max_iter；

Step2：采用反向学习策略进行种群初始化；

Step3：计算狼群个体的适应度值，选取适应度最优的个体、次优个体、第三优个体为，并且分别记录其位置；

Step4：采用式（3）更新灰狼个体位置；

2 实验及分析

实验环境为Inter（R）Core（TM）i5-5200CPU，主频2.20GHz 和内存4GB 的PC 机，操作系统采用64 位的Win⁃dows 10，编程语言采用MATLAB2018B。

为了验证IGWO 算法求解性能的优越性，选取12 基准测试函数测试算法性能。测试函数如下：Sephere（F1）、Schwefel’s Problem 2.22（F2）、Schwefel’s Problem 1.2（F3）、Generalized Rosenbrock’s（F4）、Step（F5）、Quartic Function i.e.Niose（F6）、Generalized Rastrigin’s（F7）、Generalized Grie⁃wank（F8）、Generalized Penalized（F9）、Levy Function N.3（F10）、Shekel’s Foxholes（F11）、Kowalik’s（F12）。其中F1～F6 为单峰值函数，F7～F10 是多峰值函数，F11 和F12表示固定低维函数。首先将IGWO 算法与差分进化算法（DE）、布谷鸟算法（CS）、粒子群算法（PSO）、基本灰狼算法（GWO）进行比较，验证IGWO 的性能优越性，然后将本文改进算法与其他改进灰狼算法进行对比，进一步验证算法的求解性能。

2.1 与经典算法比较

为了测试算法性能，将IGWO 算法与DE、CS、PSO、GWO 作对比，在维度D=30 下分别对每个函数独立运行30次（其中F11 搜索维度为2 维，F12 搜索维度为4 维）。选取平均精度Ave 评价算法的搜索精度，选取标准差Std 评价算法的鲁棒性，并通过观察算法的收敛曲线比较算法的收敛速度。几种算法的基本参数设置如表1 所示。

Table 1 Algorithm parameter settings表1 算法参数设置

表2 给出了IGWO 算法与各经典优化算法运行不同测试函数后的平均值和标准差，图2 为不同函数下的寻优收敛曲线。从仿真结果可以看出，改进的灰狼算法IGWO 在12 组独立实验中均一致收敛到全局最优解，尤其是求解函数F7、F8、F11、F12 时，IGWO 均能收敛到理论最优值，而其他经典优化算法均不能收敛到理论最优值。对于F1、F2、F3，与各经典的优化算法相比，IGWO 算法的求解精度和鲁棒性都具有较大优势，并且能够达到函数给定的收敛精度。例如，对于F1，IGWO 的平均值和标准差分别约是GWO 算法的约4 倍、DE 算法的29 倍、CS 算法的113 倍、PSO 算法的28 倍，求解精度和求解稳定性优势明显。对于F4、F5、F6、F9 和F10，IGWO 算法相比于其他优化算法的求解精度和求解稳定性也有一定优势。从图2 中可以明显看出，相比于DE、CS 和PSO，IGWO 算法求解速度最快，在所有测试函数上都比其他算法更快找到最优解位置。虽然GWO 算法也能取得很好的收敛效果，但是仍不及IGWO 算法的收敛性能明显，IGWO 算法较传统GWO 算法明显提升了收敛速度。因此，仿真结果表明，改进后的算法无论是收敛速度还是收敛精度，相对于基本灰狼算法都起到一定的改善效果，同时相对于其他经典优化算法都具有显著优势。

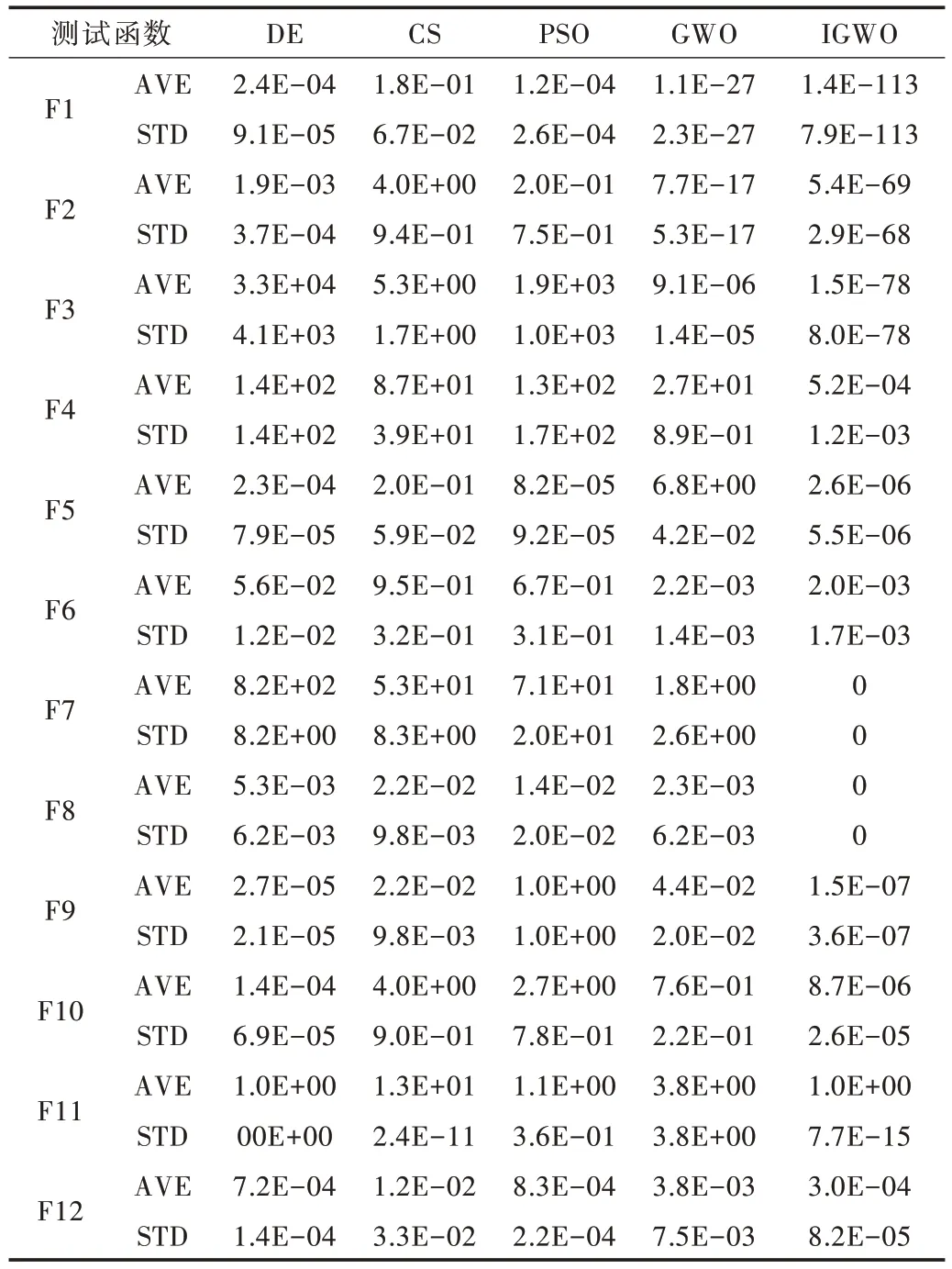
Table 2 Performance comparison with classic algorithms表2 与经典算法性能比较

Fig.2 Algorithm convergence图2 算法收敛

2.2 与其他改进算法比较

为了进一步测试IGWO 算法的寻优性能，将IGWO 算法与其他参考文献中改进的灰狼算法［19-21］进行对比。其中，mGWO 为文献［19］提出的非线性收敛的灰狼优化算法，EGWO 为文献［20］提出的进化种群动态灰狼算法，Ex-GWO 为文献［21］提出的改进位置更新方式的改进灰狼算法。通过比较算法最优解的均值以及标准差测试改进灰狼优化算法的寻优性能，对比结果如表3 所示。

平均值用于反映算法求解寻优精度，由表3 的平均值数据可知，IGWO 算法仅测试函数F6 的优化指标劣于mG⁃WO 和Ex-GWO 算法，其余测试函数优化求解效果均优于表中其他3 种改进的灰狼优化算法。对于F1、F2、F3、F7、F8 函数，IGWO 得到的各函数求解的平均值远远小于mG⁃WO、EGWO 和Ex-GWO，即IGWO 算法的求解精度远远高于mGWO、EGWO 和Ex-GWO。对于函数F4、F5、F9、F10、F11、F12，IGWO 相对于mGWO、EGWO 和Ex-GWO 算法也具有较高的求精精度。同时，标准差用于反映算法求解寻优的稳定性，由表3 的标准差数据对比可以看出，IGWO 算法对12 个测试函数的标准差值小于其他改进的灰狼算法，说明IGWO 算法的稳定性相对于mGWO、EGWO 和Ex-GWO 也较好。因此，对比其他改进的灰狼优化算法，IGWO算法在寻优性能上依然具有优势。

Table 3 Performance comparison with other improved gray wolf algorithms表3 与其他改进灰狼算法性能比较

3 结语

本文在标准灰狼优化算法的基础上，引入了反向学习策略、非线性控制因子和莱维飞行策略对标准的灰狼优化算法进行改进，提出了一种混合策略改进的灰狼优化算法。由12 个标准测试函数的仿真结果可知，IGWO 在寻优精度、稳定性和收敛速度方面不仅与经典的优化算法相比具有一定优势，同时与一些改进的灰狼优化算法相比也有一定优势。但是，本文算法未在实际问题中得到进一步验证，未来研究中，会将改进的算法应用于实际问题求解，验证算法实用性。