磁性复合流体仿贝壳抛光轨迹优化及误差分析

彭 涛

（上海理工大学机械工程学院，上海 200093）

0 引言

从古至今，人类从未停止对自然界的探索，自然界的仿生原理推动着人类文明的发展与科技的进步［1-2］。随着国内外学者对仿生材料研究的逐步深入，仿生材料在制造、医疗等行业已得到了广泛应用，对于仿生材料的加工要求也越来越高。贝壳与其它仿生材料相比，产地较广，且收集方便，研究人员已对其进行了大量研究［3］。仿贝壳角质层的仿生涂层具有耐磨性，同时又具有良好的耐水性，目前许多可降解材料虽然绿色环保，但耐水性较差，因此在材料表面涂一层仿贝壳的角质层，可在不改变绿色产品属性的前提下扩大产品使用范围［4］。贝壳由于其特殊的表面微结构，直接影响了其抗海洋污损性能，因此可将其应用于轮船及其它海洋设备上，以改善其防污性能。随着对仿贝壳工件的加工与制造越来越普遍，高精度的仿贝壳工件加工技术也需要逐步完善。目前常见的抛光技术有化学抛光、磁流变抛光、离子束抛光、磁研磨抛光技术等。

20 世纪70 年代，前苏联研发了一种磁流变液（Magne⁃torheololgical fluid，MRF）在磁场作用下的抛光技术，磁流变液是由载液、高导磁低磁滞的磁性颗粒及添加剂所组成的。美国Rochester 大学利用磁流变技术对光学元件进行抛光，以去除零件表面材料［5］；Kordonski 等［6］对石英材料的凸球面及光学元件进行磁流变抛光，获得了理想的表面粗糙度及面型误差。中科院长春光机所基于Preston 方程建立大口径光学工件磁流变加工的驻留时间算法模型，在MRF160/MRF360 数控中心上通过去除函数测试验证了模型的可靠性［7］；尤伟伟［8］基于Preston 方程和非牛顿流体润滑理论建立磁流变抛光材料去除数学模型，自主研制了一台新型磁流变仪，用于测试磁流变抛光液的流变特性是否满足抛光要求；阮承斌等［9］对磁流变液稳定性进行研究，针对在外加磁场、颗粒间相互作用及重力场作用下引起的抛光液沉淀问题采取的降低沉淀措施进行可行性分析，得出磁流变液具有高粘度、加工效率高以及抗沉淀稳定性较差的结论。21 世纪初，日本Shimada 等［10］在保留MRF 优点的基础上，研发出用于超精密加工的磁性复合流体（Mag⁃netic Compound Fluid，MCF）。MCF 不仅保留了MRF 具有的优点，还改善了MRF 抗沉淀稳定性较差的缺点［11］。对零件进行MCF 抛光时，抛光轨迹的选择尤为重要。传统的轨迹规划有直线光栅式和阿基米德螺旋线轨迹规划，张林等［12］介绍了CCOS 的轨迹抛光方法，改善了用传统方法抛光时表面产生的中、高频误差；潘日等［13］对气囊进动机构运动进行建模，通过对气囊自转运动轴运动空间进行仿真，验证了运动建模的合理性；Liu 等［14］介绍了抛光机原理，提出一种可以很好地改善中频误差的求解模型；梁奉兴［15］、樊文刚等［16］主要介绍了刀位运动时的坐标换算；Guo等［17］、Miao 等［18］分别介绍了抛光过程中工艺参数对抛光效果的影响；李爱民［19］、Lin 等［20］阐述了计算机控制小工具抛光时使用的工艺参数及其抛光特性。

然而，上述研究还未涉及到MCF 抛光仿贝壳表面的运动轨迹规划及优化。本文采用阿基米德螺旋式轨迹规划对MCF 抛光仿贝壳进行仿真，并通过改变螺旋线螺距对阿基米德螺旋式轨迹进行优化，以降低加工表面时产生的弓高误差，从而改善加工后的仿贝壳工件表面质量，为后续研究仿贝壳表面的防污性能起到指导作用。

1 抛光路径规划及仿真

1.1 抛光路径规划算法

用直线光栅式抛光轨迹对旋转对称的抛光区域进行抛光时，因为待抛光区的曲率变化较大，因此从一个抛光点移动到下一个抛光点时，抛光头的姿态需要进行大幅调整，不利于保持相对稳定的抛光状态，从而对抛光效率和抛光质量造成影响。当抛光区域为旋转对称时，用螺旋线式抛光轨迹可以均匀覆盖抛光区域，而且抛光过程中抛光状态相对稳定，因此本文推荐使用螺旋线式抛光轨迹。

为了对仿贝壳表面抛光进行研究，仿贝壳表面方程可表示为：

根据上述仿贝壳表面方程，采用螺旋式抛光轨迹进行路径规划。P0为抛光头与工件表面接触的任意点，在加工过程中根据抛光头中心轴与接触点P0法线之间的夹角（即进动角）始终相等的条件，可求出点P0(x0,y0,z0)关于工件表面的单位法矢量n→(h,i,j)。其中，有：

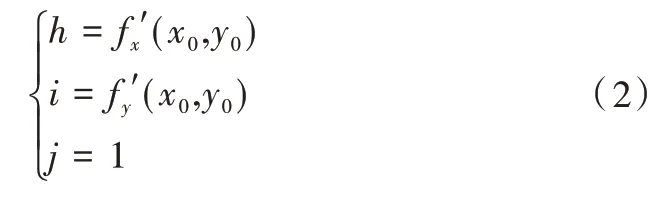
抛光头加工中心如图1 所示，根据接触点P0、单位法矢量n→和加工坐标N(xn,yn,zn)三者之间的几何关系可求出抛光头加工中心坐标：

其中，r 为抛光头半径。

Fig.1 Polishing head machining center图1 抛光头加工中心

1.2 抛光路径仿真

根据上述抛光路径规划算法，通过MATLAB 对抛光轨迹进行仿真，在仿真过程中设抛光头的圆弧半径为40，抛光头面形参数为1/180。仿贝壳方程参数如表1 所示。

Table 1 Parameters of imitation shell and workpiece表1 仿贝壳及工件参数

抛光轨迹和抛光头中心点轨迹仿真如图2 所示。

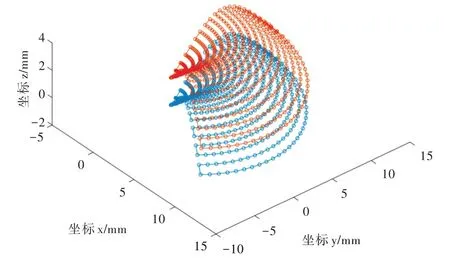
Fig.2 Movement track of center of polishing head图2 抛光头中心运动轨迹

2 抛光路径优化

2.1 阿基米德螺旋线分析

阿基米德螺旋线由于在MCF 抛光时无需换向、轨迹连续，相对于直线光栅式抛光轨迹稳定性较好，因此常用于加工回转曲面零件。阿基米德螺旋线轨迹参数方程为：

式中，θ为极角，r0表示极角为0°时的极径，k为阿基米德螺旋线系数。当k>0 时，k表示增量，ρ随着θ增大而增大；当k<0 时，k表示减量，ρ随着θ增大而减少。

采样抛光接触点如图3 所示。

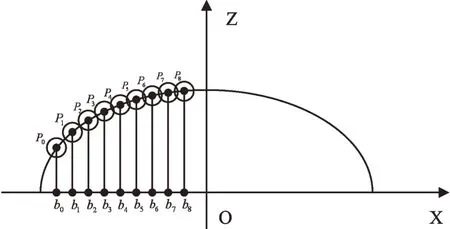
Fig.3 Sampling and polishing contact points图3 采样抛光接触点

2.2 轨迹优化算法

根据上述研究，发现如果使用螺旋式抛光轨迹对工件进行MCF 抛光，越靠近工件顶部抛光接触点越密集，越靠近底部抛光接触点越稀疏。由于抛光接触点疏密程度不同会造成抛光工件不均匀，影响零件表面加工精度。为解决上述问题，下文将介绍一种方法使得工件表面上的抛光接触点均匀分布在加工表面上。

如图4 所示，初始点P0与下一个接触点P1之间的间距为b，为了使，可将抛光接触点P0、P2看成是以点P1为圆心为半径的圆上的两点，将圆的方程与仿贝壳表面方程联立可求出两个交点，其中一个交点为P0，另一个交点就是求出的下一个抛光接触点P2，依此类推工件上的所有抛光接触点P3、P4、P5、P6…Pn。

Fig.4 Calculation of the polished contact point图4 抛光接触点计算

由上述条件可求出该圆的方程为：

圆与方程f(x,z) 的交点为P2，抛光接触点在工件表面上，所以方程可表示为：

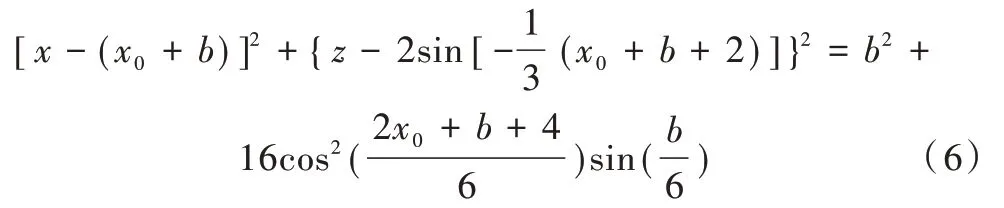
首先，初始化P0、b，可通过仿贝壳表面方程计算得出点P1的坐标；然后，根据式（5）计算出圆的方程；接下来，将计算得出的方程（6）与式（1）进行联立，可计算出P2的坐标，再以P2为圆心为半径作圆与仿贝壳表面方程进行联立，计算出点P3的坐标。以求出的交点坐标为圆心，将前后两圆的圆心距离半径与式（1）联立便可求得所有抛光接触点，且每条路径下的抛光接触点都是均匀分布的。

通过上述方法，可计算出所有路径上的抛光接触点，运用MATLAB 对优化后的抛光路径进行仿真，如图5 所示。

Fig.5 Optimal trajectory simulation图5 优化轨迹仿真

通过仿真轨迹图可看出螺旋线在边缘处比起始处更加密集，如果采用螺旋式抛光轨迹进行MCF 抛光，由于工件边缘处被抛到的部分较少，需要重新规划路径再次进行抛光，从而降低了工作效率和表面加工精度。优化后的抛光路径解决了螺旋式抛光轨迹在进行MCF 抛光时工件底部区域较顶部区域抛光接触点较少而造成抛光不均匀的问题，降低了零件表面的粗糙度，提高了零件表面加工精度。

3 加工误差分析及仿真

3.1 加工误差

弓高误差是影响仿贝壳表面加工质量的重要因素之一［21］。如图6 所示，对仿贝壳表面进行MCF 抛光时，抛光头从接触点P0加工到P1点，理想的走刀路径为弧长，但实际的走刀路线是直线，即，因此会产生弓高误差，点N到直线的距离可看作弓高误差。

Fig.6 Machining error图6 加工误差

弓高误差会影响零件加工精度，因此研究如何降低弓高误差变得尤为重要。本文研究加工误差时，假设每个抛光点上的抛光头驻留时间相等，抛光头对工件的去除轮廓形状为抛物线，抛物线方程为：

当抛光头从接触点P0(x0,y0)加工到P1(x1,y1)点，设抛光头转过的角度为θ1，P1点上的抛物线方程与P0点上的抛物线方程关系为：

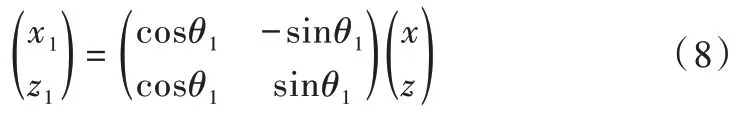
由上述关系式可得出转至P1点上的抛物线方程，联立两方程可得出交点N(xN,yN)。

抛光头从接触点P0(x0,y0)加工到P1(x1,y1)点所产生的弓高误差即为点N到线段P0P1的距离，记为d。

3.2 加工误差仿真

根据上述加工误差分析与计算，对仿贝壳表面进行MCF 抛光产生的弓高误差进行仿真。在仿真模拟中，抛光头部分的圆弧半径为40mm，仿真模拟出的弓高误差如图7所示。

MATLAB 仿真结果表明，任意角度路径上的弓高误差都呈先减小后增大的趋势。如图7 所示，在相同角度下，图7（b）相比图7（a）的弓高误差呈减少趋势。仿贝壳工件在优化后的抛光轨迹下抛光更加均匀，表面加工质量更好。

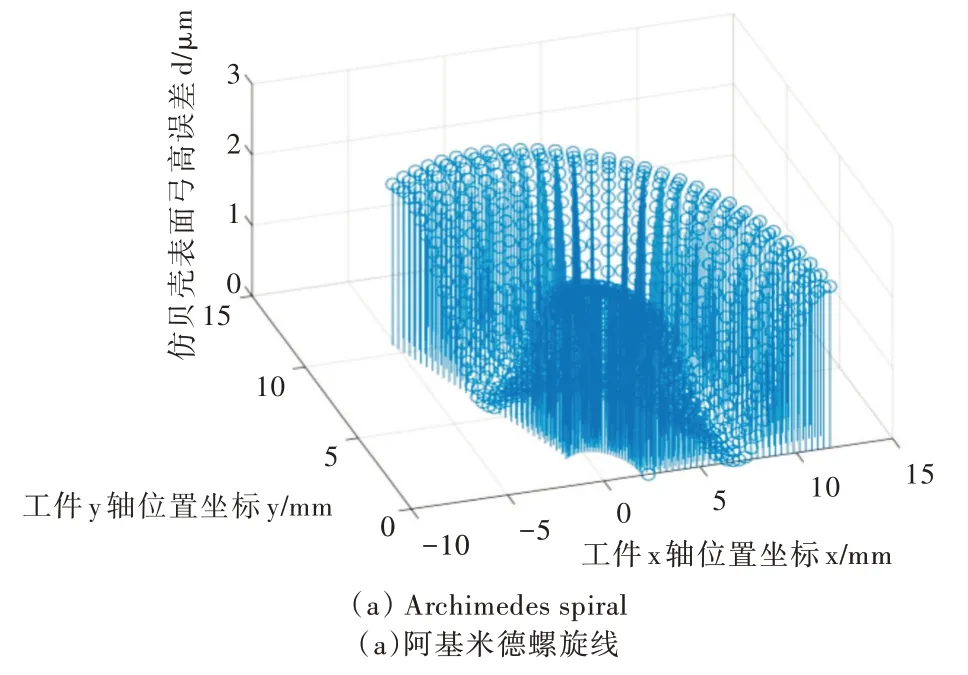
Fig.7 Arch height error distribution图7 弓高误差分布

图8 为轨迹优化前后弓高误差对比图，轨迹优化后相比优化前的弓高误差最大值从2.667μm 降低到1.841μm，弓高误差的RMS 值从1.896μm 降低到0.885μm，PV 值从2.301μm 降低到1.562μm。采用该控制算法可使抛光接触点均匀分布在工件表面，降低了弓高误差，提高了表面加工精度。

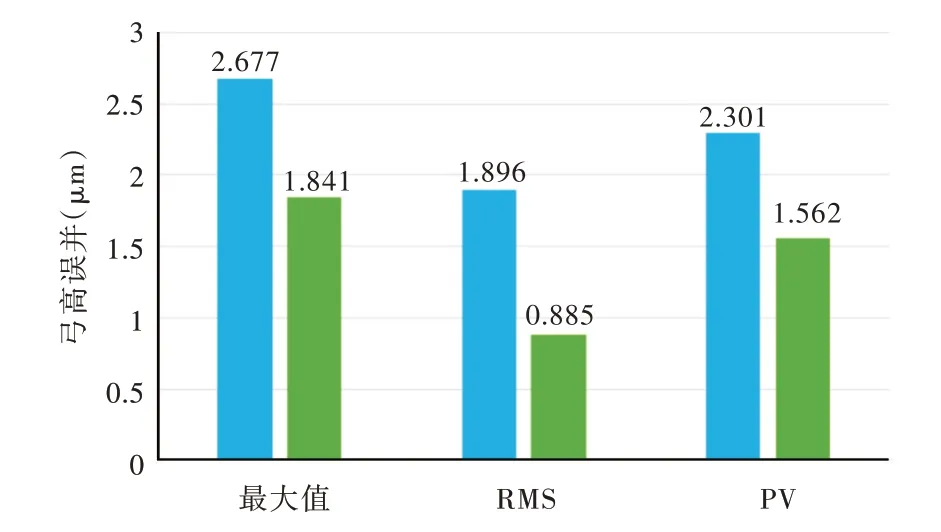
Fig.8 Comparison of bow height errors before and after trajectory optimization图8 轨迹优化前后弓高误差对比

4 结语

弓高误差是影响仿贝壳表面加工质量的重要因素。在对仿贝壳工件进行抛光时不可避免地会产生弓高误差，因此需要降低弓高误差，以提高加工精度。针对螺旋线式抛光轨迹在进行MCF 抛光时工件底部区域相比顶部区域抛光接触点较少造成抛光不均匀的问题，本文提出一种优化轨迹规划算法，并建立误差模型。通过对仿真结果的分析，结果表明，本文算法降低了弓高误差，改善了仿贝壳表面加工精度。本研究为磁性复合流体抛光仿贝壳工艺试验提供了理论依据，可降低抛光轨迹引起的弓高误差，达到理想的加工精度。