黄河源区陆面蒸散量的时空分布特征研究
陈怡璇 ,文 军 ,刘 蓉 ,陆宣承 ,陈亚玲
(1.成都信息工程大学大气科学学院/高原大气与环境四川省重点实验室,成都 610225;2.中国科学院西北生态环境资源研究所/寒旱区陆面过程与气候变化重点实验室,兰州 730000)
引言
陆面过程(Land Surface Process,LSP)通过陆-气间水、能量、动量和碳交换影响气候变化,是气候系统中最基本的物理和生化过程之一[1],同时也是影响大气环流模式(General Circulation Model,GCM)和区域气候模式(Regional Climate Model,RCM)模拟精度的主要因素之一,因此研究陆面与大气之间的相互作用非常重要。其中,陆面过程中陆-气间水分交换的一种进行方式是蒸散过程(EvapoTranspiration,ET)。蒸散过程是陆面水分通过土壤或水面蒸发以及植物蒸腾作用从地表输送到大气的过程,蒸散过程是水分在地-气系统循环过程中的重要组成部分,它连接着地-气间的能量平衡和水分循环[2],并与生态变化、资源分配和环境保护等问题有着紧密联系。研究陆面与大气之间蒸散过程的机理对人类社会的经济发展、资源利用以及生态平衡等具有科学和现实的意义。因此,对陆面蒸散过程的讨论一直以来都是地球科学领域学者们密切关注的热点[3]。
蒸散量可通过观测仪器直接或间接地获取,但由于观测环境和仪器设备技术的限制,很难实现对下垫面长时间、大范围的观测。因此,基于常规的气象观测资料构建蒸散模型来估算区域蒸散量成为当今蒸散的研究热点[4]。目前,估算蒸散量的模型主要包括:P 模型(Penman 模型)、P-M 模型(Penman-Monteith 模型)、S-W 模型(Shuttleworth-Wallace 模型)、S-S-W 模型(改进的双源模型)、P-T 模型(Priestley-Taylor 模型)、M-B 模型(McNaughton-Black 模 型)和C 模 型(Clumping 模型)等[5]。
研究表明,由于各种蒸散模型的基础理论假设不同,在实际应用时需根据研究区域的具体情况来选择适合的计算模型[6]。其中,P-M 模型将植被覆盖的下垫面视为整体来进行估算,主要适用于下垫面均一且植被密集的地区。黄河源区属于高原大陆性气候,源区内高寒植被分布广泛且均一,高寒草原和高寒草甸是其主要的植被类型,因此P-M 模型可以较为准确地模拟该地的蒸散量[5,7]。近年来,受全球气候变暖和人类活动的影响,草地退化是黄河源区近30a 来最主要的覆盖变化特征,具体表现为草地面积减小、草场质量下降和土地荒漠化面积的增加。这一变化将进一步导致物种丰富度下降,禾本科和莎草科等优势物种不断减少,高寒草地植被群落的基本结构逐渐趋于简单化[8]。
由于再分析数据具有时空连续性的特点,其在气候研究中应用价值很高。目前,已有不少利用再分析数据或卫星遥感技术开展黄河流域蒸散量的时空变化特征和影响因素的分析研究[9−12]。青藏高原地区的观测数据精度不高,空间分辨率较低[13],无法合理地表征区域尺度上气候变量的实际幅度和时间变化[14−15],因此再分析数据可作为估算蒸散量的一种辅助方式。目前的研究主要集中在黄河源区生态环境方面,对陆面蒸散量及其时空变化的研究仍比较欠缺。此外,近几年来黄河源区水分循环过程正在发生改变。因此,对于黄河源区蒸散量的长期趋势和变化原因的研究还亟待丰富。
针对上述存在的问题,本文基于修正的P-M 模型,结合气象观测数据以及陆-气间水热交换观测的试验数据,计算得到黄河源区1980~2020 年(共41a)的蒸散量,探讨该区域陆面蒸散量的长期变化趋势和空间格局,并分析影响黄河源区蒸散量变化的原因,以期为深入认识黄河源区水分循环过程、保护黄河源区生态环境和合理利用自然资源提供科学依据。
1 研究区概况
黄河源区位于青藏高原东北部,介于黄河流域的唐乃亥水文站至河源之间(95°52'~103°25'E,32°09'~36°34'N)(图1),海拔高度为3148.2~4415.4m。黄河源区集水面积约1.31×105km2,占黄河流域总面积(7.95×105km2)的16.5%,年均径流量约为2.047×1010m3,占全流域总量的35.5%[16]。
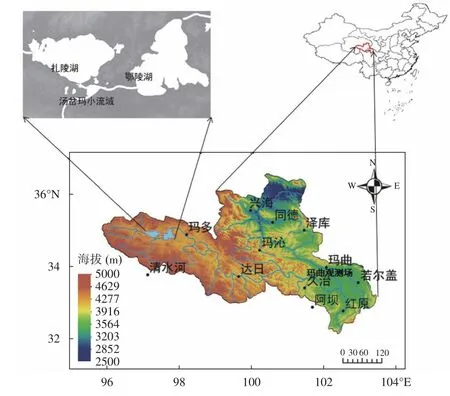
图1 黄河源区地理位置和主要气象站点分布
源区气候属于内陆高原高寒气候,年均气温约为−2.3℃,具有光照充足、辐射强、风沙大、昼夜温差大、年温差小的特点,源区内蒸散量总体呈现北高、西南低、东南变化不明显的趋势[10]。源区内植被生长周期短、分布广泛,其主要类型是高寒草原和高寒草甸[17]。该区的高寒湿地主要分布于若尔盖盆地、湖滨、三角洲及河流两侧的低洼地带以及消亡的早期湖泊,分布面积较大者有若尔盖湿地、星宿海、勒那曲入口区等[18]。
2 数据与研究方法
2.1 观测数据
基于2014 年黄河源区扎陵湖和鄂陵湖附近汤岔玛小流域的陆面过程野外观测站数据、2017 年中国科学院若尔盖高寒湿地生态研究站玛曲观测场数据以及1980~2020 年黄河源区气象台站数据,本文开展对黄河源区蒸散量的分析研究。研究区域的观测数据主要包括两类:
(1)陆-气间水热交换观测试验数据(扎陵湖和鄂陵湖附近汤岔玛小流域2014 年的陆面过程野外观测站逐日观测数据和中国科学院若尔盖高寒湿地生态研究站玛曲观测场2017 年的逐日观测数据):1.5m 高度长波辐射通量(向上、向下)和短波辐射通量(向上、向下),近地面感热通量和潜热通量,土壤温度和土壤湿度(5.0、10.0、40.0、100.0 和120.0cm 深度)。涡动观测数据主要来自于涡动相关系统,包括频率为10Hz的三维超声风速仪,CO2/H2O 气体分析仪以及数据采集器,数据采集频率为10Hz,每30min 输出一次该时段平均通量。参照《涡动相关通量观测指导手册》[19]进行处理,剔除其中不合理的数据,并对缺失的数据采用内插法进行插补,最后将结果累加,得到日尺度的平均通量值。
(2)由于气象要素在时空分布上存在差异,为综合反映黄河源区蒸散量的趋势性、周期性以及突变特征,本文选取1980~2020 年(共41a)黄河源区13 个气象站(97°~103°E,32°~36°N)的逐日观测数据,由国家气象科学数据中心(http://data.cma.cn)提供,包括:最低气温、最高气温、平均气温、平均气压、累计降水量、2min 平均风速(高度为10m)、平均水汽压、日照时数、平均相对湿度等气象要素。各气象要素的日平均值均由逐日4 次(02:00、08:00、14:00、20:00,北京时)观测数据统计得出。
2.2 研究方法
2.2.1 陆面过程水热交换观测试验方法方案和数据分析
陆面过程的能量交换与蒸散过程有着密切的联系,本研究选取了黄河源区两个区域不同年份(扎陵湖和鄂陵湖汤岔玛小流域2014 年6 月1 日~2015 年6月1 日,中国科学院若尔盖高寒湿地生态研究站玛曲观测场2017 年1 月1 日~2017 年12 月31 日)的涡动相关数据,通过这些数据计算出两地的实际陆面蒸散量。
本文通过涡动相关观测数据计算出上述两个区域的实际陆面蒸散量,应用统计回归方法将其与用修正的P-M 模型计算的蒸散量进行比对,研究两者的相关性,进而验证修正的P-M 模型的准确性。
2.2.2 P-M 计算实际蒸散量的原理和方法
1965 年,Monteith 在Penman 公式的基础上[20],提出了P-M 模型,该模型引入植被的生理特征和空气动力学参数的变化,计算精度较高且理论依据较充分,能较为准确地反映蒸散变化过程和影响机制。该模型被FAO-56 推荐为计算蒸散量的首选方法[21−22]。其中,FAO Penman-Monteith 模型是世界粮农组织(FAO)推荐计算参考蒸散量的方法,其修正模型表达式[23]如下:
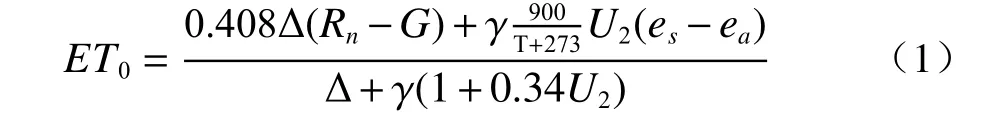
式中:ET0为参考蒸散量(mm/d);T为日平均温度(℃);U2为 2m 高处风速(m/s);es为饱和水汽压(kPa);ea为实际水汽压(kPa)
本文需要分析源区蒸散量的季度和年度数据,用以研究其时空分布特征,此时需要利用月值的气象数据来计算。在应用修正的P-M 模型计算蒸散量时,不能直接把日值数据对应月值数据来计算,每个参数都需要进行重新换算。计算时需注意:
(1)相对于净辐射Rn,土壤热通量G的值很小,当时间尺度为1~10d时,G通常忽略不计;但当计算时间尺度较长时,此项不能忽略,计算公式为:

式中:G为土壤热通量( MJ·m−2·d−1);ca为土壤热容量( MJ·m−2·℃−1);Ti为 时刻i的 空气温度(℃);Ti−1为时刻i−1的 空气温度(℃);Δt为时间步长(d);Δz为有效土壤深度(m)。
当时间尺度以月为单位时,假设土壤深度适当、土壤热容量为常数2.1M J·m−2·℃−1,可用下式估算:

式中:Tm,i为 第i月的平均气温(℃);Tm,i−1为上月的平均气温(℃);其中,假设首月的土壤热通量为0。
(2)用修正的P-M 模型计算蒸散量时,需用到地表净辐射这一要素。地表净辐射可由气象观测的辐射数据直接计算得出,但由于气象观测站和辐射观测站数量不匹配(全国辐射观测站共130 个,气象观测站共699 个),且观测年份不统一,导致辐射资料在连续性分析和趋势分析中不易与气象数据相结合。因此,在计算蒸散量时,一般通过气象观测数据间接地计算地表净辐射,而不用辐射数据,具体计算步骤参照《气象干旱等级》[24]。
3 黄河源区蒸散量时空分布及变化原因
3.1 实际蒸散量的观测与计算结果对比分析
修正的P-M 模型估算的是参考作物的蒸散量,涡度相关法观测的是实际陆面蒸散量。在干旱地区,没有达到水分盈余的条件,实测的蒸散量要比用修正的P-M 模型估算出的蒸散量低,而涡度相关法存在能量平衡不闭合的问题,会造成对蒸散量的估算值偏低[25]。修正的P-M 模型计算的参考作物蒸发蒸腾量,与实际观测值接近[23]。已有研究表明:在不同下垫面,修正的P-M 模型是计算蒸散量的最好方法[25],两种方法所得蒸散值虽有一定偏差,但若两者相关性好、变化趋势一致,则说明P-M 法能较好地估算区域实际蒸散量。
通过黄河源区扎陵湖和鄂陵湖汤岔玛小流域2014 年和中国科学院若尔盖高寒湿地生态研究站玛曲观测场2017 年的每日涡动相关数据计算出当地的蒸散量,并与修正的P-M 模型计算的蒸散量进行比对,结果见图2。
由图2 可知,涡动相关数据和修正的P-M 模型计算的蒸散量变化趋势大体一致,扎陵湖和鄂陵湖汤岔玛小流域的月均蒸散量夏季高,冬季低;12 月蒸散量最小,其实际蒸散量为10.27mm,7 月蒸散量最大,其实际蒸散量为64.80mm。中国科学院若尔盖高寒湿地生态研究站玛曲观测场的月均蒸散量的季节变化
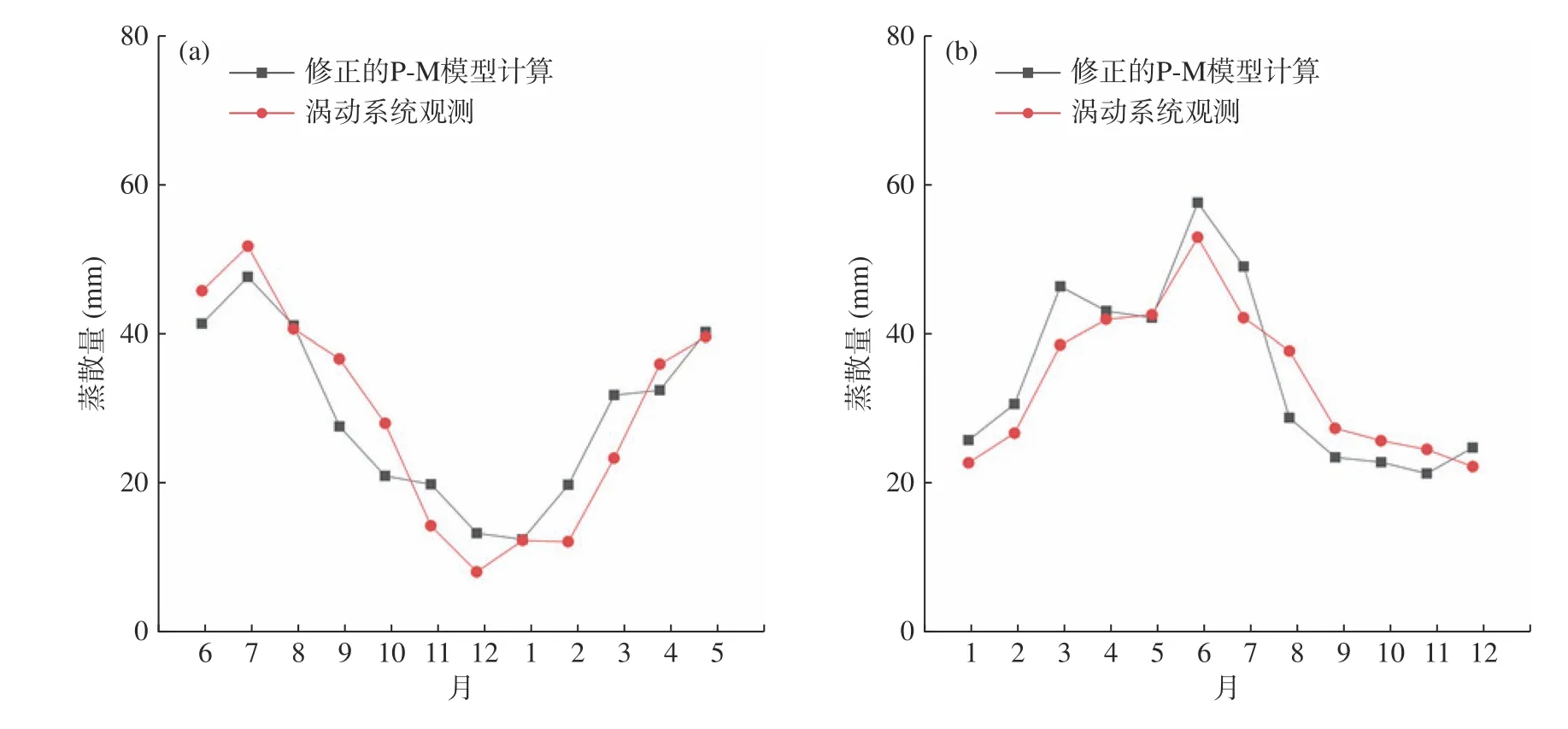
图2 涡动相关数据与修正的P-M 模型计算的蒸散量对比(a.2014 年扎陵湖和鄂陵湖汤岔玛小流域的月均蒸散量,b.2017 年中国科学院若尔盖高寒湿地生态研究站玛曲观测场的月均蒸散量)
与扎陵湖和鄂陵湖汤岔玛小流域的相似,12 月蒸散量最小,其实际蒸散量为28.07mm,6 月蒸散量最大,其实际蒸散量为66.54mm。修正的P-M 模型计算出的蒸散量与实际陆面蒸散量的年总量相差不大,在扎陵湖和鄂陵湖汤岔玛小流域分别为437.26mm 和435.40mm;在若尔盖高寒湿地生态研究站玛曲观测场分别为523.36mm 和510.12mm。为了进一步验证两种模式计算出的蒸散量的相关性,对两地的涡动相关数据和修正的P-M 模型算出的蒸散量进行线性回归处理,结果如表1 所示。
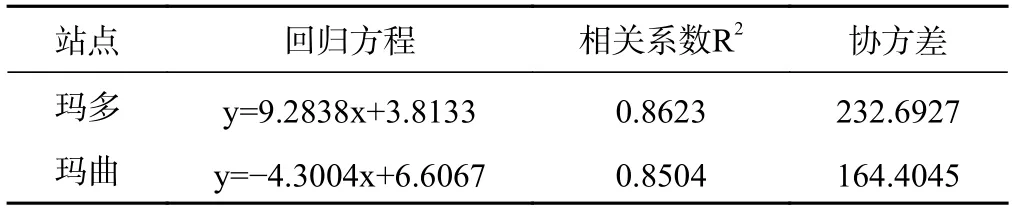
表1 涡动相关数据与修正的P-M 模型计算的蒸散量的回归方程
通过比较回归方程的相关系数和协方差(表1),易知涡动相关数据和运用修正的P-M 模型计算出的蒸散量具有较好的正线性相关,可见运用修正的PM 模型计算蒸散量的准确性较高。
3.2 黄河源区不同站点蒸散量变化趋势分析
本文以一年为时间尺度,分析每个站点1980~2020 年(共41a)的蒸散量变化趋势。按照东西走向,将黄河源区分为东部、中部和西部三个区域,结合各个观测站的数据,运用修正的P-M 模型计算得出每个站点的年均蒸散量,统计每个区域的蒸散量,绘制黄河源区蒸散量的时间变化序列,如图3、图4 和图5所示。
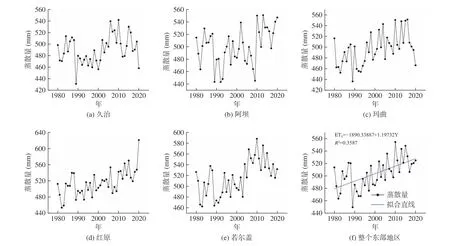
图3 1980~2020 年黄河源区东部年均蒸散量
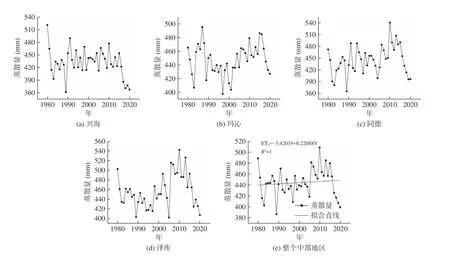
图4 同图3,但为黄河源区中部
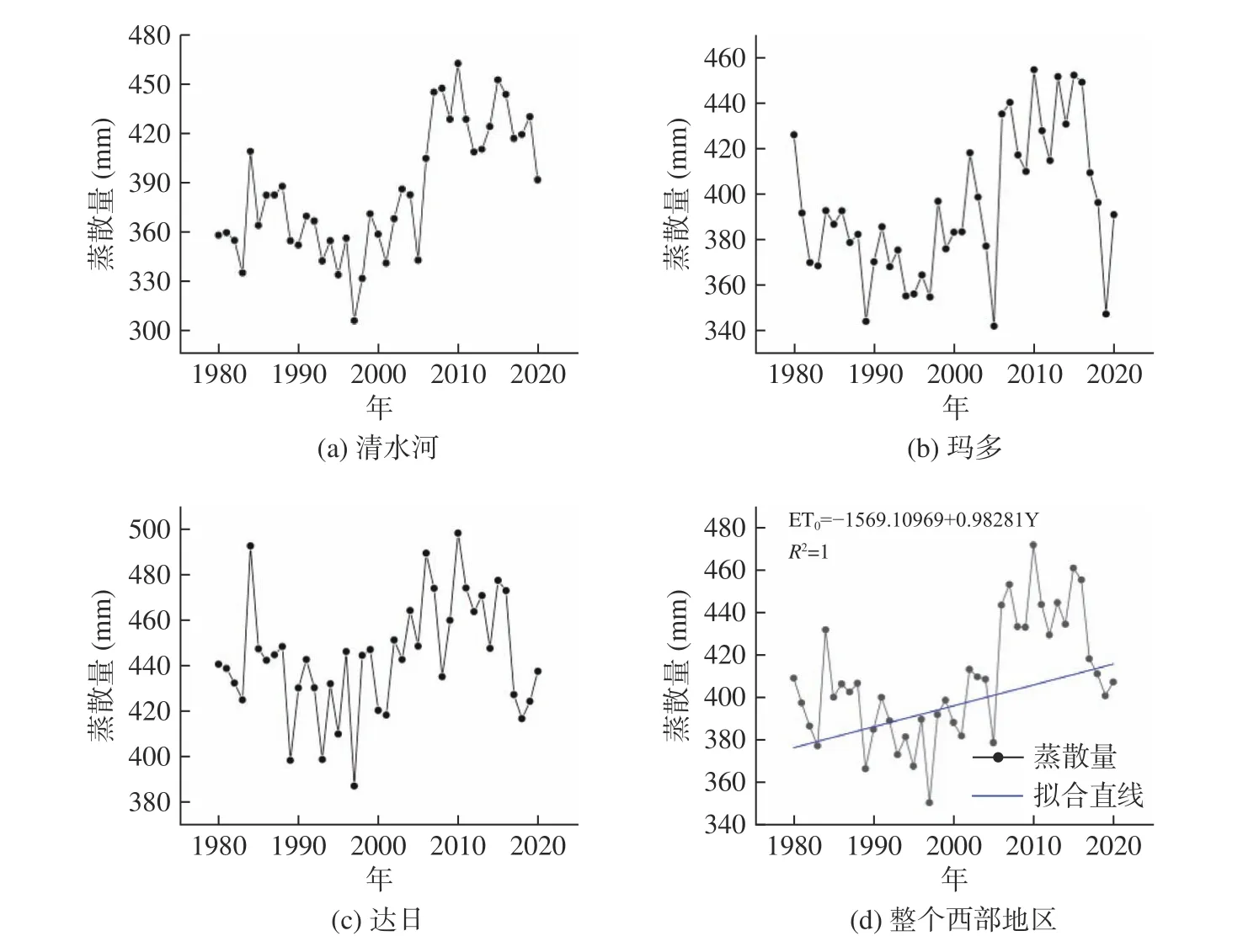
图5 同图3,但为黄河源区西部
从各个站点来看,其年均蒸散量波动振幅较大,这可能是年均降水、日照等影响因素导致的。从区域平均看,东、中、西部的年均蒸散量分别为504.30mm、445.19mm、408.56mm。由拟合直线可以看出,1980~2020 年黄河源区的蒸散量总体呈上升趋势,但各个区域的蒸散量在20 世纪80 年代中期和90 年代中期均呈显著减少趋势,近年来中部和西部地区的蒸散量总体上呈减少趋势,而东部地区的蒸散量总体上呈增加趋势。不同时间段内,蒸散量的变化存在一定空间差异,蒸散量大小的区域分布大致为:东部地区>中部地区>西部地区。
对各个站点的蒸散量累加求平均,得到黄河源区总体蒸散量。图6 给出了1980~2020 年黄河源区陆面蒸散量的时间变化序列及线性趋势。如图所示,黄河源区蒸散量总体呈增长态势,其变化趋势与西部地区和中部地区的一致,均在20 世纪80 年代中期和90 年代中期呈显著减少态势,进入21 世纪后,总体蒸散量呈增加态势,但在2015 年后又有减少的趋势。
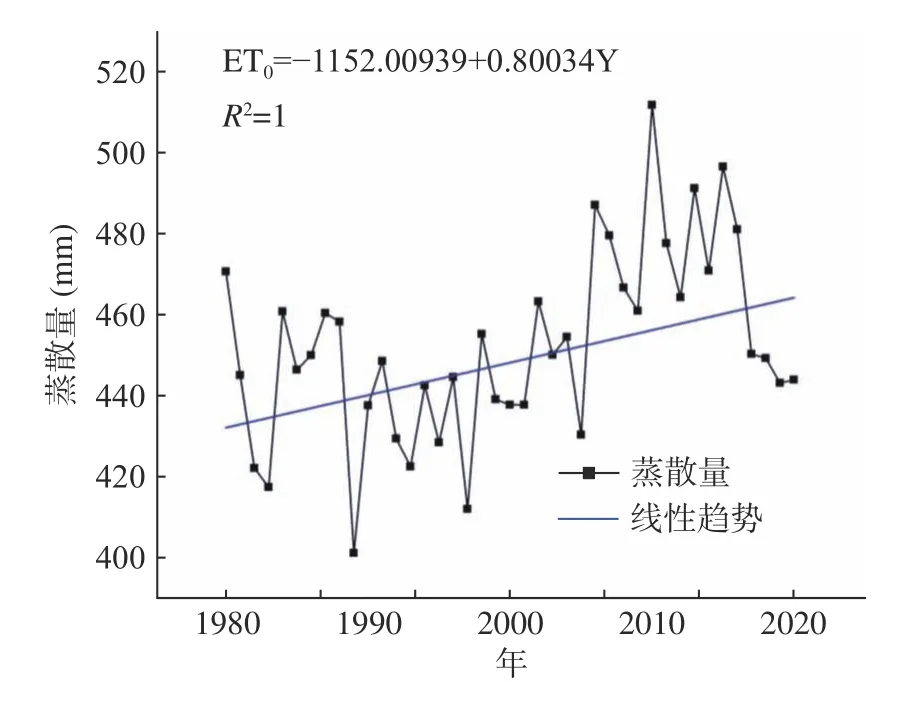
图6 黄河源区的陆面蒸散量时间变化序列及线性趋势
3.3 黄河源区陆面蒸散量空间分布
为了揭示黄河源区蒸散量的空间分布特征,本文依据1980~2020 年气象台站观测数据,在ArcGIS环境下通过反距离加权(Inverse Distance Weighted,IDW)插值法[26−27]绘制出源区内四季蒸散量的时空分布(图7)。如图所示,黄河源区蒸散量的季节分布东西差异明显;春季蒸散量为117.8~162.8mm,夏季蒸散量为140.5~179.4mm,秋季蒸散量为78.0~105.5mm,冬季蒸散量为50.1~78.7mm,分别占年蒸散量的31.2%、34.6%、19.9%、14.3%,即为夏季>春季>秋季>冬季。
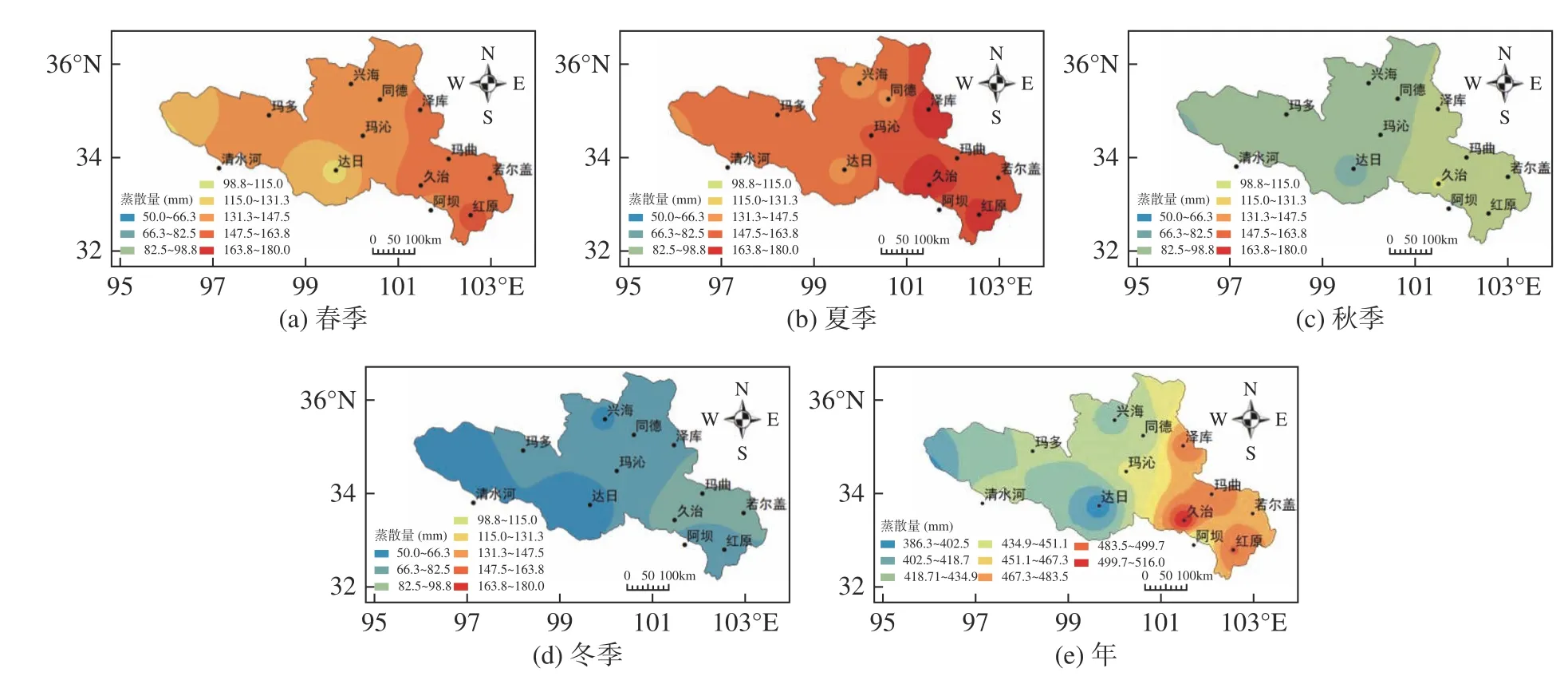
图7 多年平均的黄河源区四季及年蒸散量时空分布
多年平均的年蒸散量为386.3~516.0mm,其空间分布与季节蒸散量的基本一致。东部地区蒸散量为473.5~516.0mm,红原地区的蒸散量最大,约为516.0mm;中部地区蒸散量为437.6~473.5mm,地理分布为从东到西逐渐减小;西部地区蒸散量为386.3~437.6mm,从东到西呈先增后减特征,其中清水河地区的蒸散量最小,约为386.3mm。总体来看,西部地区的蒸散量低于东部地区,整个黄河源区的蒸散量从东到西逐渐减少。
3.4 影响黄河源区蒸散过程的气候因子
已有研究[28]指出影响蒸散过程的主要因素是土壤和气象因素:(1)影响土壤蒸散过程的土壤因素可分为土壤的结构、质地、色泽、含水量,地下水埋深以及地表特征等;(2)气象因素主要包括气温、降水方式、湿度、辐射、风速等。
为了解影响黄河源区蒸散过程的气象因素,本研究以黄河源区年均蒸散量为因变量做逐步回归分析[29],将气象观测的年均数据逐个引入模型,发现蒸散量与最高气温、最低气温、平均气温、日照时数、平均相对湿度、平均风速和降水量7 个影响因子有较高的相关性,进而得到逐步回归方程:

式中:ET0、Tm、Tn、T、n、RH、U、PRE分别代表蒸散量、最高气温、最低气温、平均气温、日照时数、平均相对湿度、平均风速、降水量。
为分析影响黄河源区蒸散过程的气候因子,应用复相关系数法[30−31]得出复相关系数r=0.9840,表明蒸散量与以上7 个影响因子的线性拟合度较高,各变量之间有很好的线性相关关系。进一步分析发现,该相关关系通过了0.001 水平的显著性检验。
由于偏相关分析是在排除其他变量的影响后分析两变量间相关关系的分析方法,其强调因变量对每个自变量的依赖关系。因此,本研究利用偏相关分析[32]对蒸散量与各个影响因子的关系进行探讨。
通过对影响蒸散过程的影响因素进行偏相关分析(表2),结果表明:蒸散量分别和平均风速、日照时数有显著的线性正相关(P<0.01),与平均气温有线性正相关,但相关性不显著(P>0.01);蒸散量分别和最高气温、最低气温、平均相对湿度、降水量有线性负相关性,与平均相对湿度有极显著的相关性(P<0.01),而与最高气温、最低气温的相关性不显著(P>0.01)。因此,蒸散量随温度、风速和日照时数的增加而增大,随相对湿度和降水量的增大而减小。
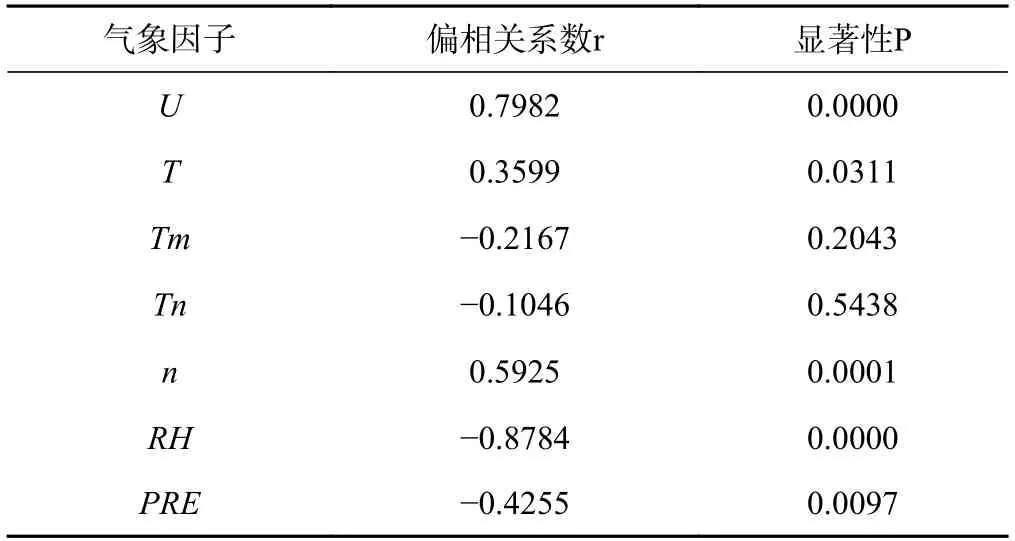
表2 蒸散量与不同气象因子的偏相关系数和显著性
气候要素变化的时空差异复杂多样,在不同区域特定的气候条件下,同一气候要素对蒸散过程的作用不尽相同,水汽压、温度和净辐射等影响要素的不同组合也会导致蒸散量的增加或减少。偏相关分析结果表明:蒸散量与温度、风速和日照时数的变化趋势相同,与相对湿度和降水量的变化趋势相反。
4 结论
本文利用修正的P-M 模型计算出1980~2020 年黄河源区的陆面蒸散量,选取黄河源区扎陵湖和鄂陵湖汤岔玛小流域和中国科学院若尔盖高寒湿地生态研究站玛曲观测场两个地区的涡动相关数据,检验了修正的P-M 模型估算源区蒸散量的准确性,并利用反距离加权插值法分析了源区内蒸散量的时空分布,运用逐步回归分析等方法探讨了蒸散量与不同气象个影响因子有较高线性相关性。由偏相关分析可知,蒸散量随温度、风速和日照时数的增加而增大,随相对湿度和降水量的增大而减小。

