基于最大熵原理的强对流大风灾害致灾能力指数研究

曾翔宇 ,马 力 ,朱克云

（1.成都信息工程大学大气科学学院，成都 610225；2.四川省气象局，成都 610072）

引言

据统计，气象灾害占据自然灾害总数的60%以上，而气象灾害所造成的损失是自然灾害中最为严重的[1]。强对流大风灾害是一种突发性的灾害性天气，常常能在很短时间内产生很大风速，对社会生产、人类生活造成巨大影响[2]，因此强对流大风灾害的致灾能力评估十分重要。对于强对流大风灾害的风险评估，国内外专家开展了大量研究，并取得了良好的进展，使其在气象灾害的防灾减灾工作中发挥了关键作用[3−14]。Lekes 等[4]通过研究不同风速对森林产生的不同影响，对强对流大风灾害进行了预测和评估。Lee 等[5]研究结合了承载体的易损度，对台风灾害进行了分析，并对其进行灾害评估。Katz 等[6]以GDP 作为宏观经济参考，将灾害造成的经济损失数据定量化处理，以经济作为承灾体易损性因子，对台风灾害进行灾害风险评估研究。张学文[7]在气象学研究中引入了熵原理，提出了“熵气象学”一词，即每一次灾害性天气过程，可以视为其熵达到最大，系统的空气微团所具有能量的释放过程，由此会产生灾害性天气的分布律函数。刘小艳等[8]通过分析孕灾环境、致灾因子、承灾体、灾情4 个风险因子，提出了全新的气象灾害风险评估思路，并对比了德尔菲法、专家打分法、层次分析法3 种常见风险评估方法的原理和优缺点。李德友等[9]利用分钟降水资料，基于DEM、地貌特征、土地利用类型、土壤类型和土壤湿度程度等地理信息数据，模拟并评估了暴雨-泥石流灾害。周懿等[10]选取资阳地区51 个地面观测站风场资料和micaps 高空填图资料，应用二元回归法建立了大风预报方程。张丽娟等[11]通过研究1971～2005 年黑龙江省78 个市（县）的大风时空分布数据，结合信息扩散理论的计算方法和气象灾害风险评估的基本理论，得出了不同强对流大风灾害发生日数的概率风险值，并使用GIS 技术做了风险区划。夏祎萌[12]利用1960～2010 年东疆铁路沿线测风站的风速数据和强对流大风灾害数据记录，对东疆铁路沿线的强对流大风灾害进行了风险评估。王孝萌[13]基于GIS 系统，设计了一套气象灾害风险评估系统，应用CSharp 编程语言，实现气象灾害的调查图制作、灾害风险区划图制作以及气象灾害的风险评估模块。魏海宁[14]介绍了灰色关联度方法的理论和国内外的相关研究成果，最终选取了2007～2009 年辽宁省本溪市气象灾害数据，运用灰色关联度方法和气象灾害损失评估模型对这3 年的气象灾害进行了分析。刘璐[15]选取了16 个灾害评估指标，从各类致灾条件出发，利用灰色关联度方法对宁波市台风灾害的风险进行了评估，建立了新的台风灾害风险等级标准。

由于气象灾害种类较多，致灾机制和致灾途径均不相同，目前仍在使用大量文字和图表来描述灾害状况，缺少一个能够定量表征灾害性天气时间、空间、强度的指数，严重阻碍了气象灾害评估业务水平的提升。针对这一问题，本文拟以最大熵原理为基础，结合灰色关联度法，构建表征强对流性大风灾害天气过程的致灾能力指数，并选取四川省强对流大风灾害天气个例进行检验。

1 数据来源及研究方法

1.1 数据来源

研究使用了2009～2019 年四川省4123 个自动观测站的2min 平均风速数据。选取了8 场强对流大风灾害天气个例，对应灾害所造成的实际经济损失统计数据来自四川省气象台决策服务中心。

1.2 研究方法

最大熵原理是本文的主要理论基础[16]，根据此理论能拟合出可以表征强对流大风灾害天气过程时间、空间、强度的概率分布函数，再通过分布函数找出相应的气象参量，构建致灾能力指数公式。具体研究思路如下：

（1）基于最大熵原理，根据统计数据，拟合出表征每一场强对流大风灾害天气过程时间、空间、强度的概率分布函数，并进行显著性检验。

（2）根据强对流大风灾害天气的概率分布函数，找出可以完整表征强对流大风灾害天气过程时间、空间、强度的气象参量。

（3）利用灰色关联度法，以强对流大风灾害的直接经济损失为参考，进行气象参量的关联度计算，求出每个参量的所占权重。

（4）构建出表征强对流性大风灾害天气过程的致灾能力指数。

（5）对强对流大风灾害天气的致灾能力指数进行个例检验。

2 强对流大风分布函数拟合及检验

2.1 强对流大风分布函数推导

选取个例中的2min 平均风速与对应的持续时间作为强对流大风天气的基本要素，利用最大熵原理推导其概率分布规律，首先将风速作为离散变量x，并以风速达到7m/s 作为底数分为若干变量，每个变量有相应的持续时间作为概率p与之对应，如表1 所示：

表1 变量与概率对应表

熵（H）为概率论角度定义的一个量，离散变量的熵公式为：

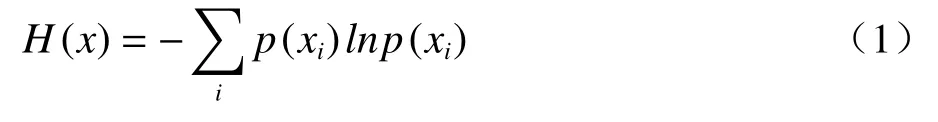
则可得，风速与对应持续时间的熵公式为：

利用拉格朗日乘子法，构造一个新的泛函带入原熵公式中，将原熵公式逐步化简，可得到分布函数。

即风速与持续时间为负指数关系，则风速与持续时间对数呈线性分布函数关系。

2.2 分布函数拟合及检验

基于最大熵原理对强对流大风灾害天气分布函数推导，可得出风速与持续时间呈负指数关系，而风速与持续时间的对数呈线性函数分布，所以可对大风灾害个例进行线性分布函数拟合，公式如下：

利用最小二乘法[17]，计算k、b值，对强对流大风天气过程个例进行函数拟合，公式如下：

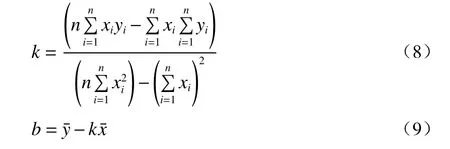
最小二乘法是依据某个事件的大量观测结果，而获得“最佳”的结果或是“最有可能”的表现形式[18]。将强对流大风灾害的的风速（x）以及持续时间对数（y）代入上式，并拟合出概率分布函数，可得表2。

表2 强对流大风灾害概率分布函数拟合结果

对拟合的分布函数进行F检验[19]。将风速作为x，代入拟合函数中，可计算出理论值，将其与持续时间对数，分别代入F检验公式，见式（10）和（11）。其检验结果如表3 所示。

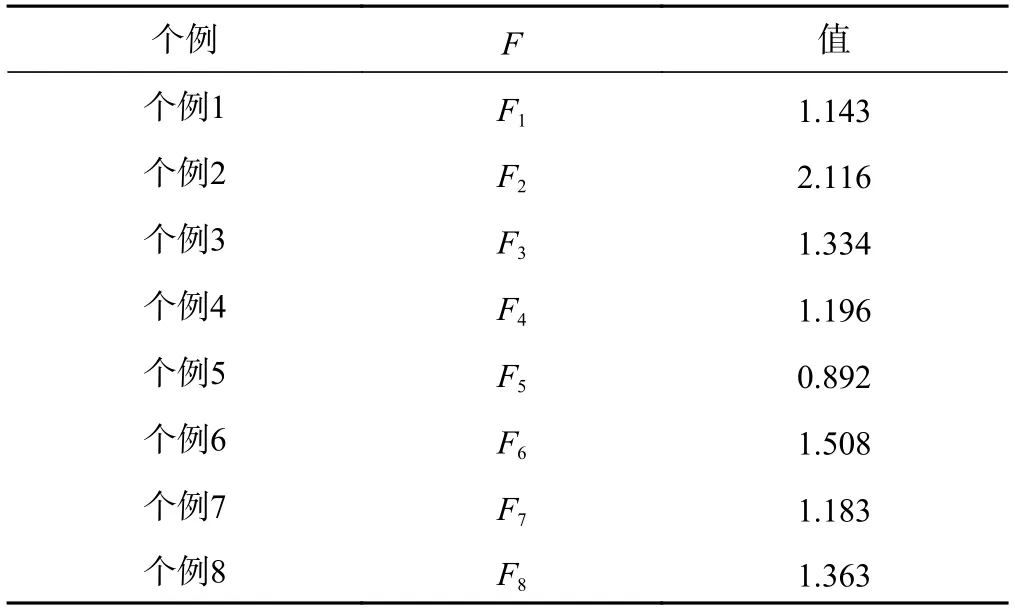
表3 强对流大风灾害个例F 值对比表

根据自由度（k,n−k−1）（n为样本总量，k为样本分组的组数），设显著性检验水准α=0.05。比较Fα=0.05(k,n−k−1)与F值发现，个例的F值均小于Fα=0.05，即理论值与实际值并无显著性差异，因此强对流大风灾害的风速与持续时间对数呈线性关系。

基于最大熵原理拟合出的强对流大风灾害分布函数克服了时间和空间的局限，可以表征强对流大风灾害的时间、空间及强度，具有普适性。

3 大风致灾能力指数计算及检验

3.1 气象参量选取

根据分布函数的拟合结果，强对流大风灾害的风速与持续时间对数呈线性分布关系，则分布函数可得出k值这一主要气象参量，由于k值是强对流大风灾害分布函数中风速平均值的变相表达形式，因此气象参量中选取过程平均风速来表征。由于本文仅针对强对流大风灾害天气，所以不考虑大风灾害的空间覆盖范围要素，综合线性分布函数的其余要素，选取可以体现时间和强度的参量来表征强对流大风过程的情况。

本文选取风速达到10m/s 的持续时间来表征时间特征，选取强对流大风灾害过程最大风速来表征强度特征，加上过程平均风速，总共3 个参量来完整地表达大风灾害的致灾能力，并且统计每场个例的直接经济损失，结果见表4。

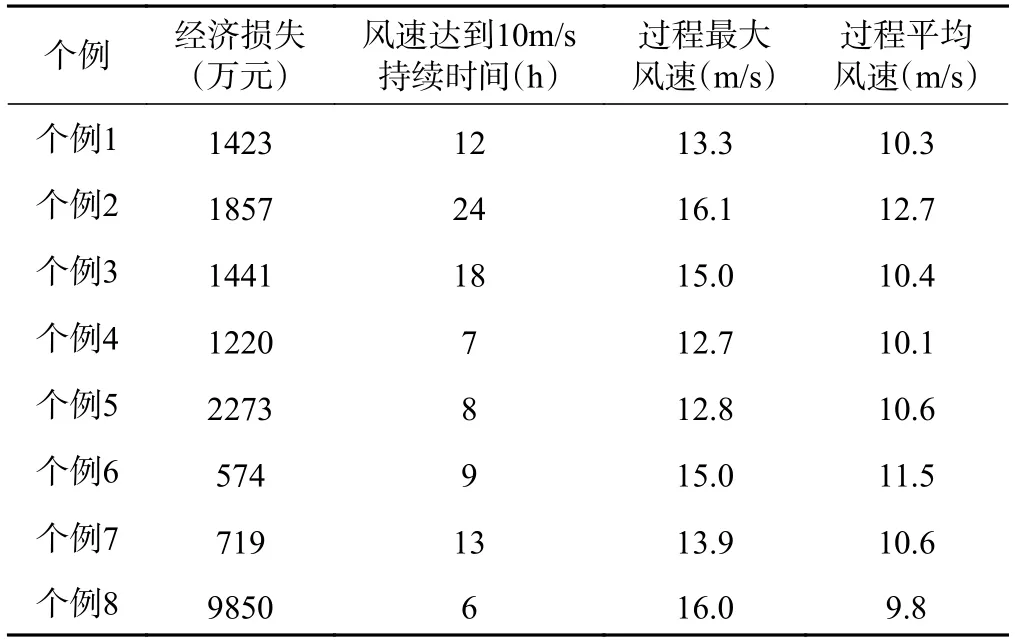
表4 强对流大风灾害统计参量表

3.2 致灾能力指数计算公式

根据表4 的气象统计参量，利用灰色关联度计算方法[20]列出矩阵，以经济损失作为参考数据，计算强对流大风灾害各个参量之间的灰色关联度，具体公式如下：

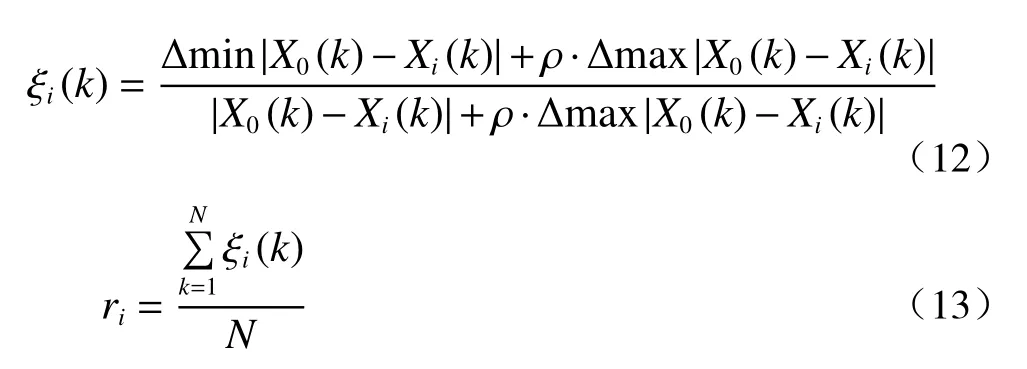
式（12）中：ρ为分辨系数，在(0，1)区间内取值，通常为0.5；若 ρ越小，则关联度系数间的差异性越大，区分能力越强；Δminmin|X0(k)−Xi(k)|为第二级最小差，Δmaxmax|X0(k)−Xi(k)|为 第二级最大差。式（13）中：ri为关联度值，N为个例数量。各参量之间的灰色关联度见表5。

表5 强对流大风灾害参量灰色关联度

由上述关联度结果，计算各个气象参量的权重，见式（14）。各个参量在灾害过程中所占权重见表6。

表6 强对流大风灾害参量所占权重

式中：a、b、c为上述强对流大风灾害气象参量。

根据表6 可知，过程最大风速所占的权重最大。强对流大风灾害天气致灾能力指数的计算公式如下：

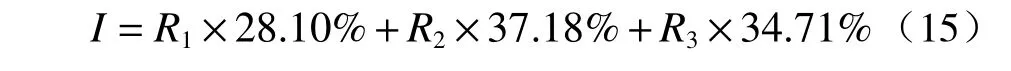
式中：R1为风速达到10m/s 持续时间，R2为过程最大风速，R3为过程平均风速。

3.3 个例检验

根据上述强对流大风灾害天气致灾能力指数计算公式，选取发生在四川省2017 年夏季、2018 年春季、2019 年夏季的三场直接经济损失和气象参量值均不相同的强对流大风灾害天气个例进行检验分析，三场强对流大风灾害天气的风速与持续时间、风速与持续时间对数关系分别如图1、图2、图3 所示。

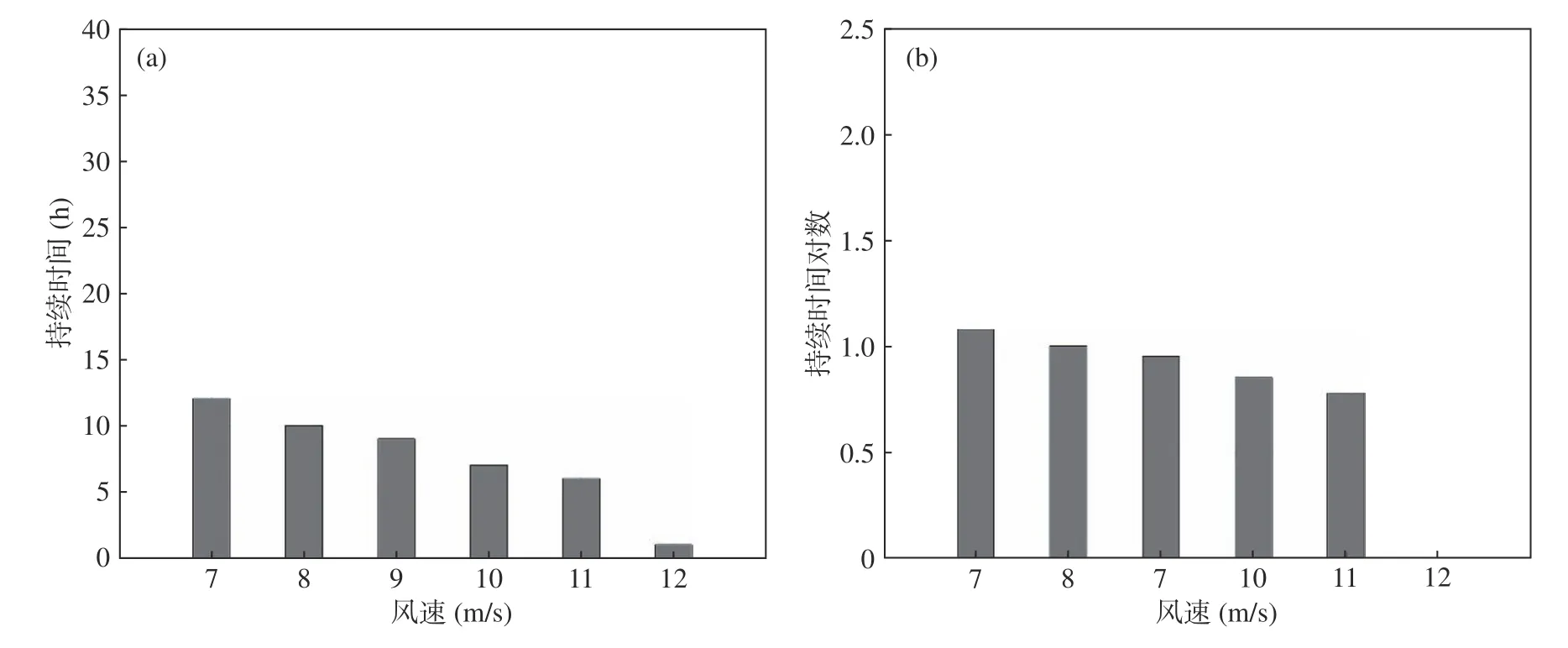
图1 2017 年7 月15 日（a）风速与持续时间关系和（b）风速与持续时间对数关系

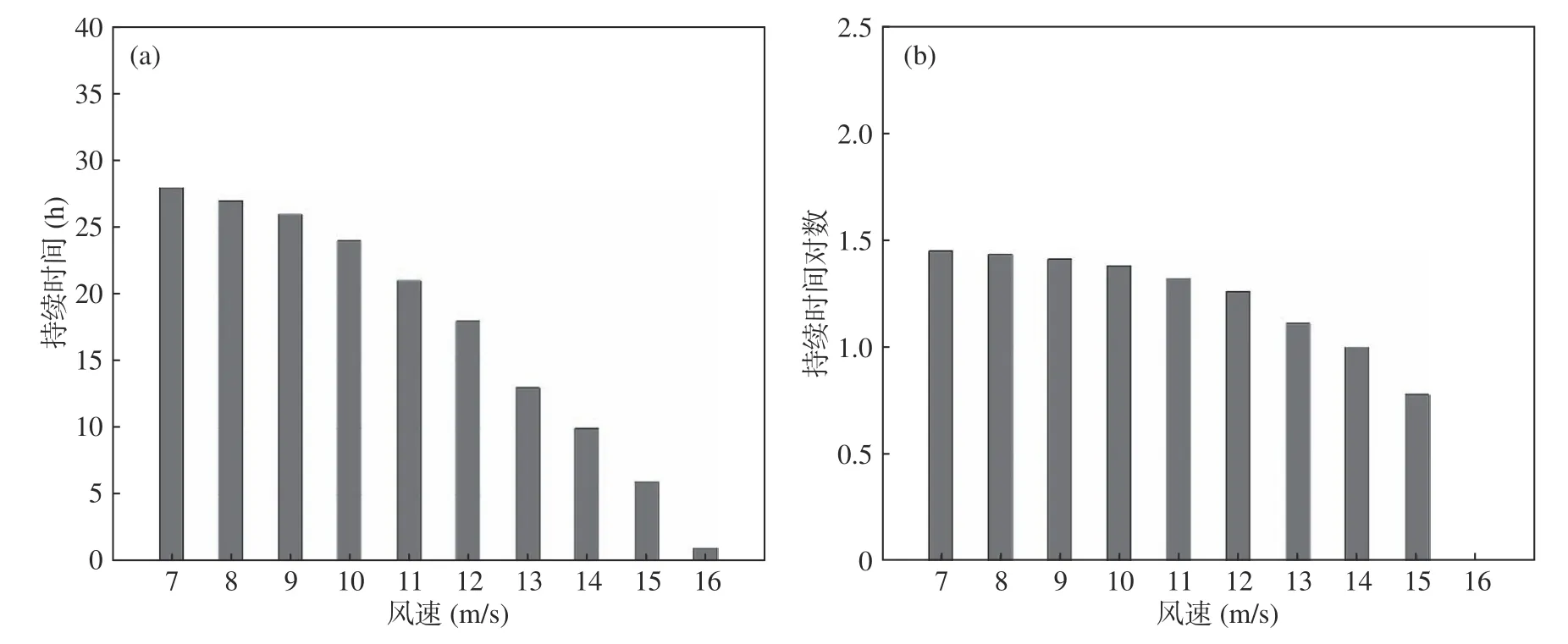
图2 同图1，但为2018 年4 月4 日

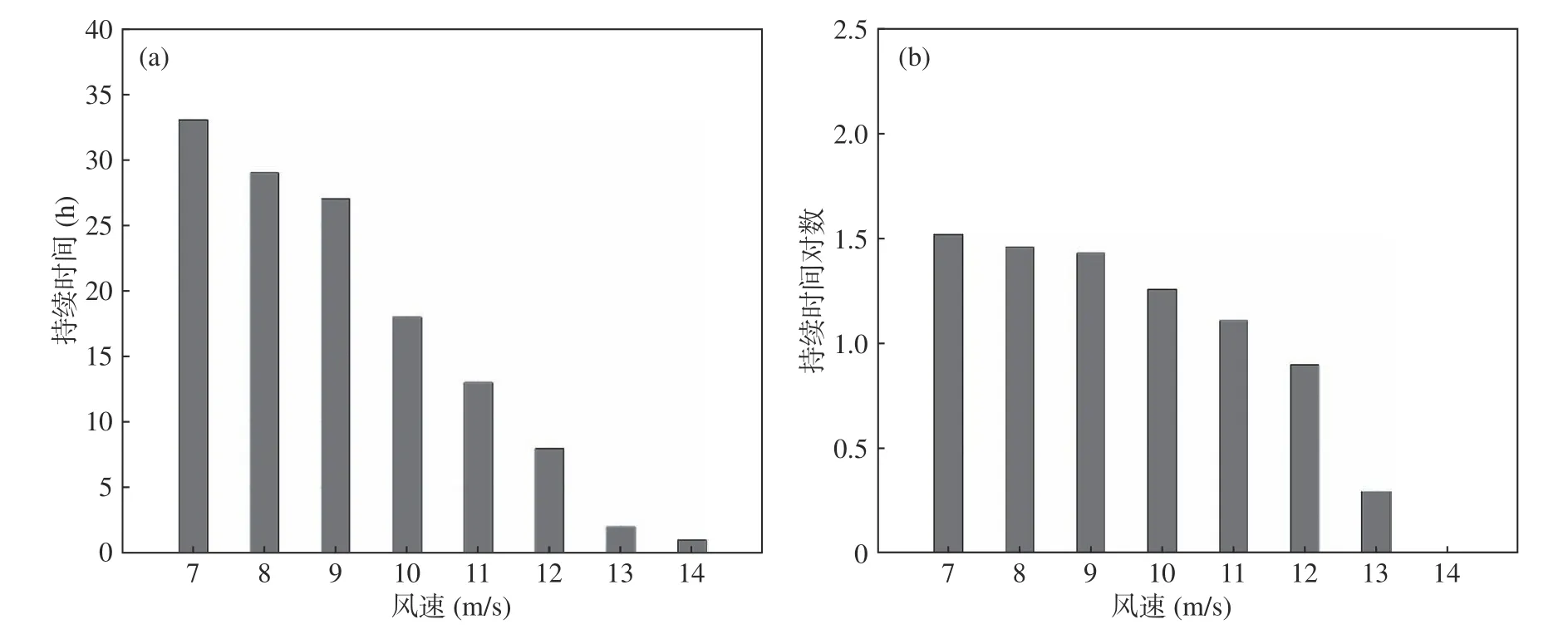
图3 同图1，但为2019 年7 月23 日

三场强对流大风灾害天气对当地造成了不同程度的损失，其中2018 年强对流大风灾害天气造成的直接经济损失最大，达1867 万元，灾害过程的最大风速达16.1m/s，过程平均风速为12.7m/s，风速达到10m/s 的持续时间为24h；2019 年强对流大风灾害天气造成的直接经济损失达1441 万元，灾害过程的最大风速达15.0m/s，过程平均风速为10.4m/s，风速达到10m/s 的持续时间为18h；而2017 年造成的直接经济损失损失最小，达1220 万元，灾害过程的最大风速达12.7m/s，过程平均风速为10.1m/s，风速达到10m/s的持续时间为7h。

将三场强对流大风灾害天气的最大风速、过程平均风速、风速达到10m/s 的持续时间3 个气象参量代入致灾能力指数公式进行计算，结果如表7 所示。

对表7 进行归一化处理，结果如表8 所示。

表7 强对流大风灾害致灾能力指数

由表8 可知，2018 年强对流大风灾害致灾能力指数大于2017 和2019 年的致灾能力指数，对比三场灾害天气过程的气象参量及灾害直接经济损失数据，致灾能力指数可以准确反映强对流大风灾害过程的致灾能力强度，即指数越大，致灾能力越强，反之则越弱。

表8 强对流大风灾害致灾能力指数（归一化）

4 结论与讨论

本文以最大熵原理为基础，结合灰色关联度法，构建表征强对流性大风灾害天气过程的致灾能力指数，并选取四川省强对流大风灾害天气个例进行检验，得出如下结论：

(1)基于最大熵原理拟合出的强对流大风灾害分布函数克服了时间和空间的局限，可以表征强对流大风灾害的时间、空间及强度，具有普适性。

(2)结合灰色关联度法，基于最大熵原理建立的强对流大风灾害致灾能力指数能准确表征其致灾能力的大小，可在气象灾害评估业务中推广应用。

本文只是对强对流大风灾害致灾能力评估方法行了初步探讨，如再结合对实际承灾体的暴露度、脆弱性、易损性等要素的考量，则强对流大风灾害的风险评估结果会更为直观、全面。