基于经验-解析数据的某核电安全壳地震易损性分析

王晓磊，吕大刚，阎卫东

(1.沈阳建筑大学 土木工程学院，辽宁 沈阳 110168；2.河北省地震灾害防御与风险评价重点实验室，河北 三河 065201；3.哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090)

核电厂地震安全评估包括抗震裕量评估(SMA)[1]和地震概率风险评估(SPRA)[2]两种方法。SPRA是基于全概率公式的核电厂地震安全评估方法，可定量分析核电厂地震安全评估中包含的各种不确定性，分析结果较SMA更为精细。由于地震危险性分析技术的进步，已运行核电厂厂址地震危险性水平可能发生变化，需对该核电厂厂址上的核电厂结构、系统和部件重新进行地震安全评估[3]。

地震易损性分析是SPRA中的重要组成部分。目前安全系数法是核电厂常用的地震易损性分析方法，其数据来源主要包括解析易损性数据、经验易损性数据、专家判断易损性数据和混合易损性数据等。文献[4]指出混合易损性数据由于综合多种数据源的优点，相对其他数据源更具优势。我国已运行了一些核电厂，由于地震危险性分析技术进步和实际地震发生等原因，这些已服役核电厂厂址地震危险性(审查水平地震和厂址谱等)可能发生变化。基于混合数据的地震易损性方法研究，对我国已运行核电厂地震安全评估具有重要借鉴意义。

本文基于经验-解析数据对某核电安全壳地震易损性分析进行研究。

1 核电厂地震易损性分析

1.1 地震易损性安全系数法

地震易损性安全系数法[5]是目前核电厂结构、系统和部件常用方法，基本原理可简述如下。

核电厂结构、系统和部件抗震能力A[6-9]可表示为：

A=AmeReU

(1)

式中：Am为核电厂结构、系统和部件抗震能力中位值；eR和eU为假设服从对数正态分布的随机变量(中位值为1，标准差分别为βR和βU)，分别代表本质不确定性和知识不确定性。

安全系数法将抗震能力表示为安全系数与设防地震能力乘积的形式：

A=F·ASSE

(2)

式中：F为抗震能力安全系数；ASSE为安全停堆地震能力。

安全系数F进一步可表示为：

F=FS·Fμ·FRS

(3)

式中：FS为强度系数；Fμ为塑性能吸收系数；FRS为响应系数。

(4)

式中：S为某种失效状态下单元抗震能力；RN为非地震荷载下的单元响应；RT为所有荷载作用下(包括地震荷载)的单元响应。

FRS=FSA·FSD·FM·FMC·Fδ·FEC·FSSI

(5)

式中：FSA为谱型系数；FSD为随着深度地震动输入折减系数；FM为建模系数；FMC为模态组合系数；Fδ为阻尼系数；FEC为地震分量的组合系数；FSSI为土-结相互作用系数。

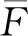
(6)

(7)

(8)

βFRS=

(9)

1.2 基于混合易损性数据的核电安全壳地震易损性分析方法

本文基于地震易损性安全系数法，采用混合易损性数据对服役核电厂安全壳进行地震易损性分析，具体步骤为：生成核电厂场地相关条件谱，选取匹配场地相关谱的地震动记录，进行安全壳增量动力分析(IDA)，IDA结果为安全系数FS和FSA的中位值和标准差，安全系数法中的其他系数采用经验数据，将解析易损性数据和经验易损性数据整合为混合易损性数据，最终生成核电厂安全壳地震易损性曲线。

2 基于经验-解析数据的我国某核电安全壳地震易损性分析

2.1 某核电安全壳力学模型

本文分析对象为我国华南地区某核电厂核岛厂房，其三维剖面图和简化模型[10]如图1所示，核岛中安全壳和筏板基础简化模型信息及材料参数参考文献[10]。本文采用开源程序OpenSees进行有限元建模和分析，模态分析结果列于表1。

a——剖面图；b——简化模型

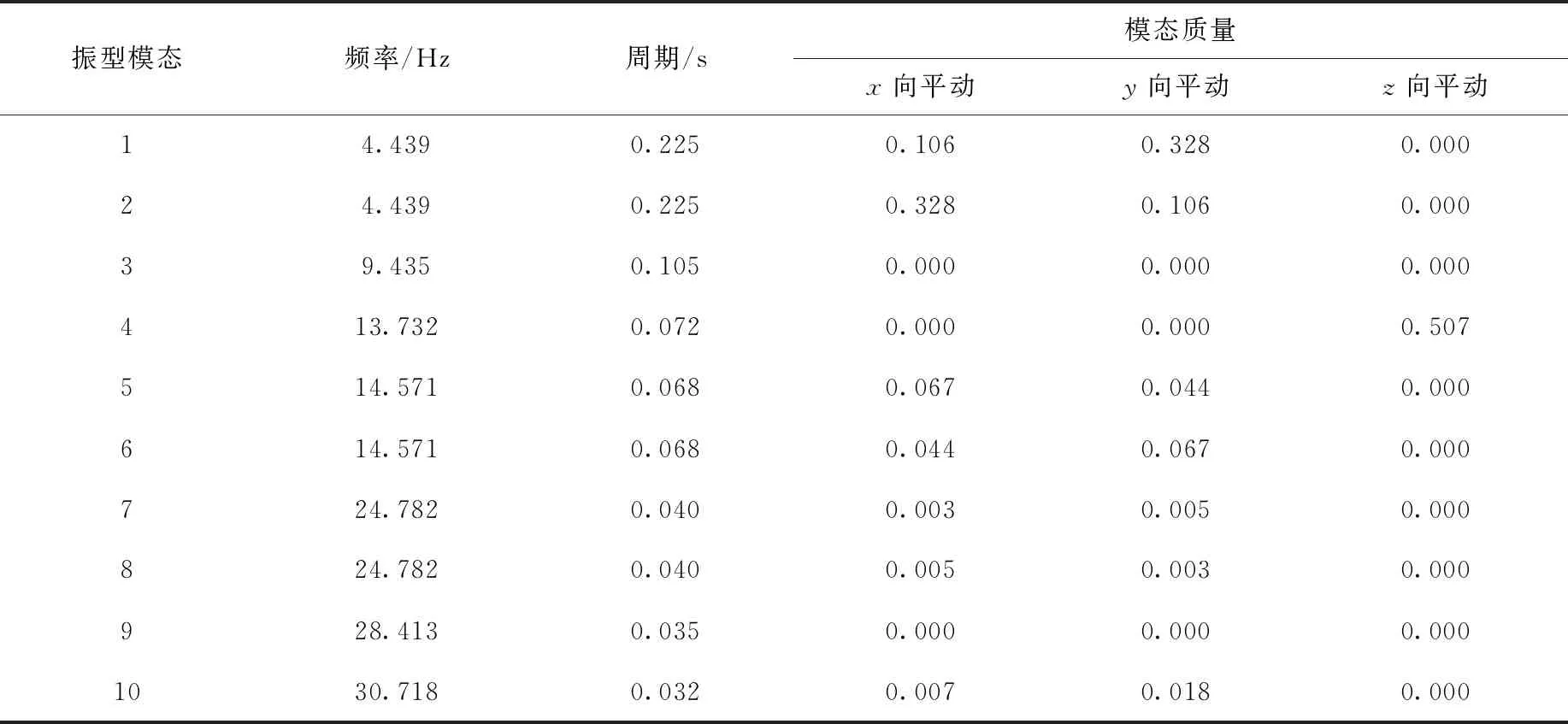
表1 安全壳简化模型模态分析结果

安全壳是核电厂最后一道安全屏障，其完整性十分重要。本文假设当在地震中安全壳处于塑性状态时，安全壳即失效。安全壳应力应变关系可表示为三线性骨架曲线模型[11]，如图2所示，取第一个拐点为安全壳极限状态，此剪应力极限值τ1[11]为：

(10)

式中：FC为混凝土抗压强度；σV为竖向压应力。

2.2 某核电厂厂址条件谱和地震动记录选取

2.2.1某核电厂厂址条件谱 场地相关谱是地震危险性分析的副产品，其中，一致危险谱是早期被广泛应用的场地相关谱，有学者发现一致危险谱较为保守，在一致危险谱基础上，Baker等[12]提出了条件均值谱。条件均值谱相较于一致危险谱进一步考虑了谱型相关性，更符合真实地震动反应谱形式。

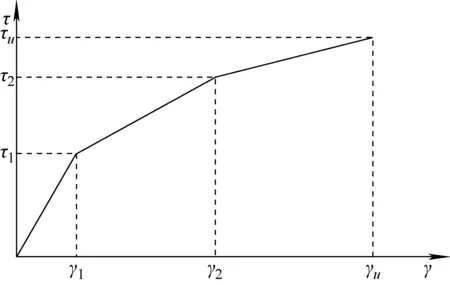
图2 三线性骨架曲线

条件均值谱μln Sa(Ti)|ln Sa(T*)的理论公式[12]为：

μln Sa(Ti)|ln Sa(T*)=μln Sa(M,R,Ti)+

ρTi,T*ε(T*)σln Sa(Ti)

(11)

式中：μln Sa和σln Sa为基于地震动预测方程的ln Sa(Ti)的预测平均值和标准差，Sa(Ti)为周期为Ti的谱加速度；ρTi，T*为相关系数；M为震级；R为距离；T*为条件周期；Ti为预测周期；ε(T*)为条件周期T*处的谱型参数，ε(T*)可以表示为：

(12)

在条件均值谱的基础上，进一步考虑条件标准差可生成条件谱，条件谱考虑了场址谱的分布(条件标准差)信息。条件标准差σln Sa(Ti)|ln Sa(T*)[13]可表示为：

(13)

将我国华南地区某核电厂厂址作为算例场地，该场地包含1个地震统计区：空间范围为北纬19°～24°、东经109°～116°，Mmax(最大震级)为8.00，b值(古登堡-里克特公式参数)为0.87，ν4(四级以上地震年平均发生率)为5.60，h(震源深度)为15 km，包含32个潜在震源区，如图3所示。

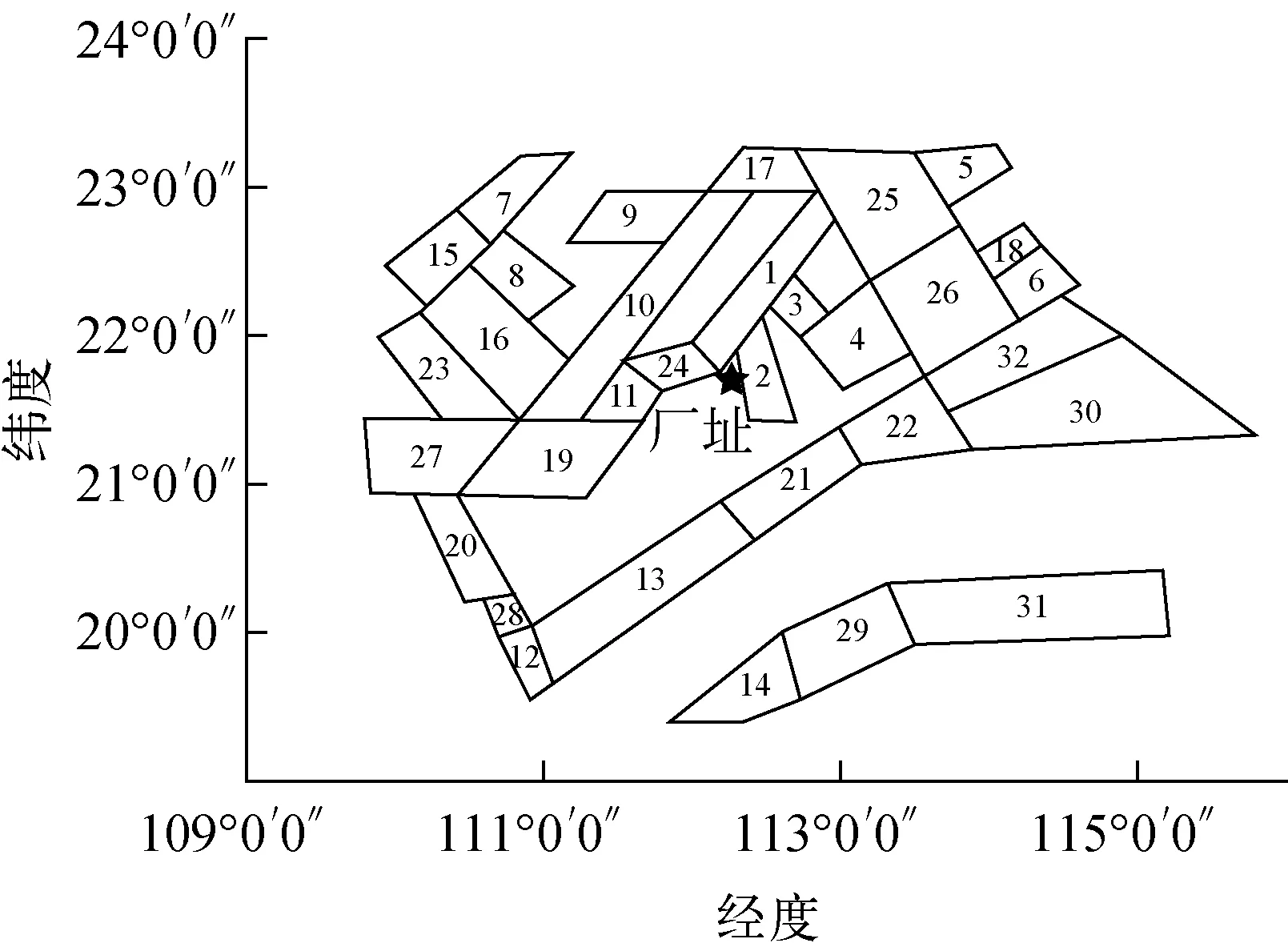
图3 厂址潜在震源区分布

地震动预测方程(GMPE)采用霍俊荣[14]分析给出的华南地区GMPE，可表示为：

lgY=C1+C2M+

C3lg(R+C4exp(C5M))+σlg Yε

(14)

式中：C1、C2、C3、C4和C5为系数；ε为服从标准正态分布的一个随机变量，代表lgY的观测变量；σlg Y为GMPE的预测标准差。

图4 厂址地震危险性曲线

表2 平均值设定地震(万年一遇)

2.2.2地震动记录选取 本文采用Baker等[16]提出的基于贪心优化算法的地震动记录挑选方法，具体理论如下。

选取的地震动与目标谱的误差可由地震动对数谱加速度与目标谱对数谱加速度差值的平方和SSE表示：

(15)

式中：ln Sa(Tj)为被选地震动调幅后在周期为Tj的对数谱加速度；ln Sa(s)(Tj)为模拟目标谱在周期为Tj的对数谱加速度；p为周期个数。

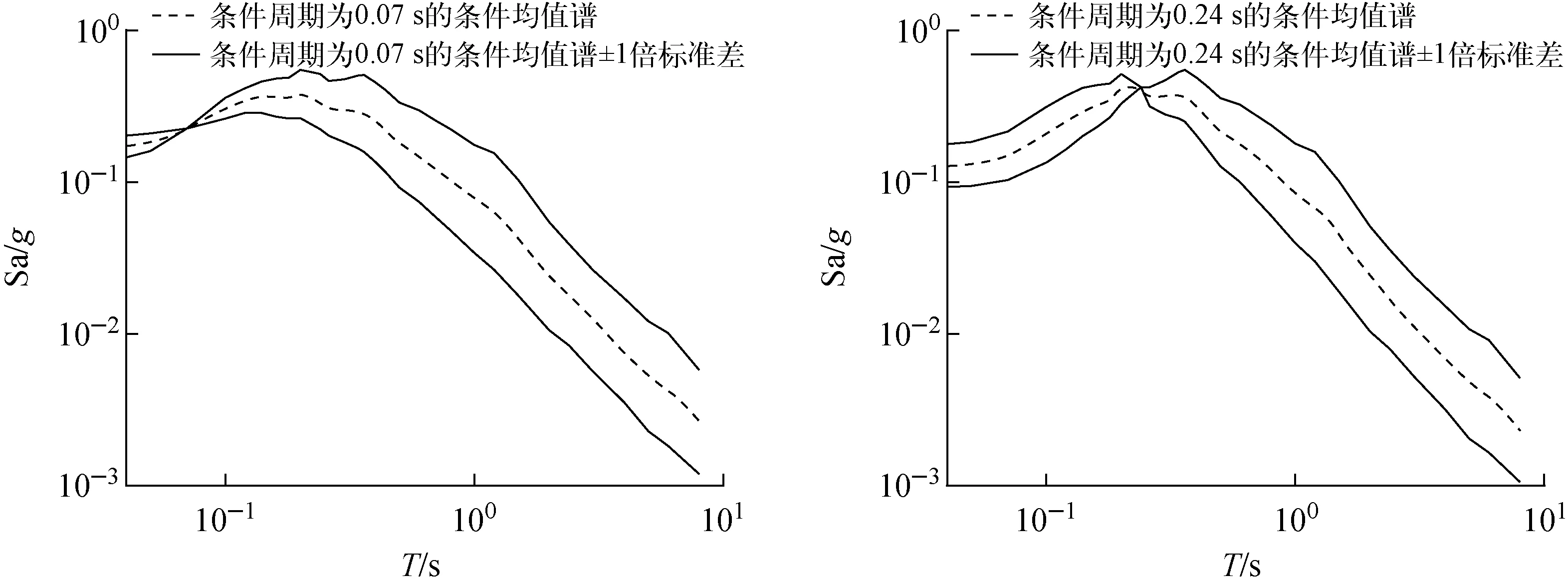
图5 算例核电厂条件谱

被选地震动对数谱加速度平均值与目标谱对数谱加速度平均值的最大百分数误差ERRmean可表示为：

(16)

式中：mln Sa(Tj)为被选地震动在周期为Tj的对数谱加速度的样本平均值；μln Sa(Tj)为场地目标谱在周期为Tj的对数谱加速度平均值。

被选地震动对数谱加速度标准差与目标谱对数谱加速度标准差的最大百分数误差ERRstd可表示为：

(17)

式中：sln Sa(Tj)为被选地震动在周期为Tj的对数谱加速度的样本标准差；σln Sa(Tj)为目标谱在周期为Tj的对数谱加速度的标准差。

上述两类误差的权重误差平方和SSEs可表示为：

w(sln Sa(Tj)-σln Sa(Tj))2]

(18)

式中，w为权重系数，表示平均值和标准差两类误差的相对重要性。

基于贪心优化算法的地震动选取方法步骤简述如下[16]：首先以条件谱(式(11)、式(12)和式(13))为目标谱，基于统计模拟方法生成模拟谱，然后基于最小SSE准则(式(15))初选地震动记录，判断选取地震动记录是否满足式(16)和式(17)误差要求(容许误差为10%)，如不满足，基于式(18)并运用贪心优化算法进一步选取地震动记录，反复上述过程，直到选取地震动记录满足式(16)和式(17)为止，最终输出地震动选取结果。

以图5所示的条件谱分别为目标谱，基于上述地震动记录选取方法，最终挑选了两组地震动记录，挑选的地震动记录与目标谱拟合情况分别如图6、7所示，可发现：选取的地震动记录可很好匹配目标谱的均值和标准差。

2.3 基于IDA的解析易损性数据

本文采用IDA方法得到易损性函数的中位值和标准差，易损性函数中位值和标准差的估计值[17]可表示为：

(19)

(20)

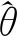
基于本文选取的两组地震动记录，采用IDA方法生成拟合易损性曲线，如图8a、b和图9a、b所示，得到解析易损性数据，列于表3。将IDA方法计算的地震动解析易损性数据与其他参数经验易损性数据(表4)结合，可生成易损性曲线，如图8c和图9c所示。

a——模拟地震动的反应谱；b——选取地震动的反应谱；c——中位值Sa；d——对数Sa的标准差

a——模拟地震动的反应谱；b——选取地震动的反应谱；c——中位值Sa；d——对数Sa的标准差

a——IDA；b——基于IDA结果拟合易损性曲线；c——地震易损性曲线

a——IDA；b——基于IDA结果拟合易损性曲线；c——地震易损性曲线

表3 IDA拟合的解析易损性模型参数

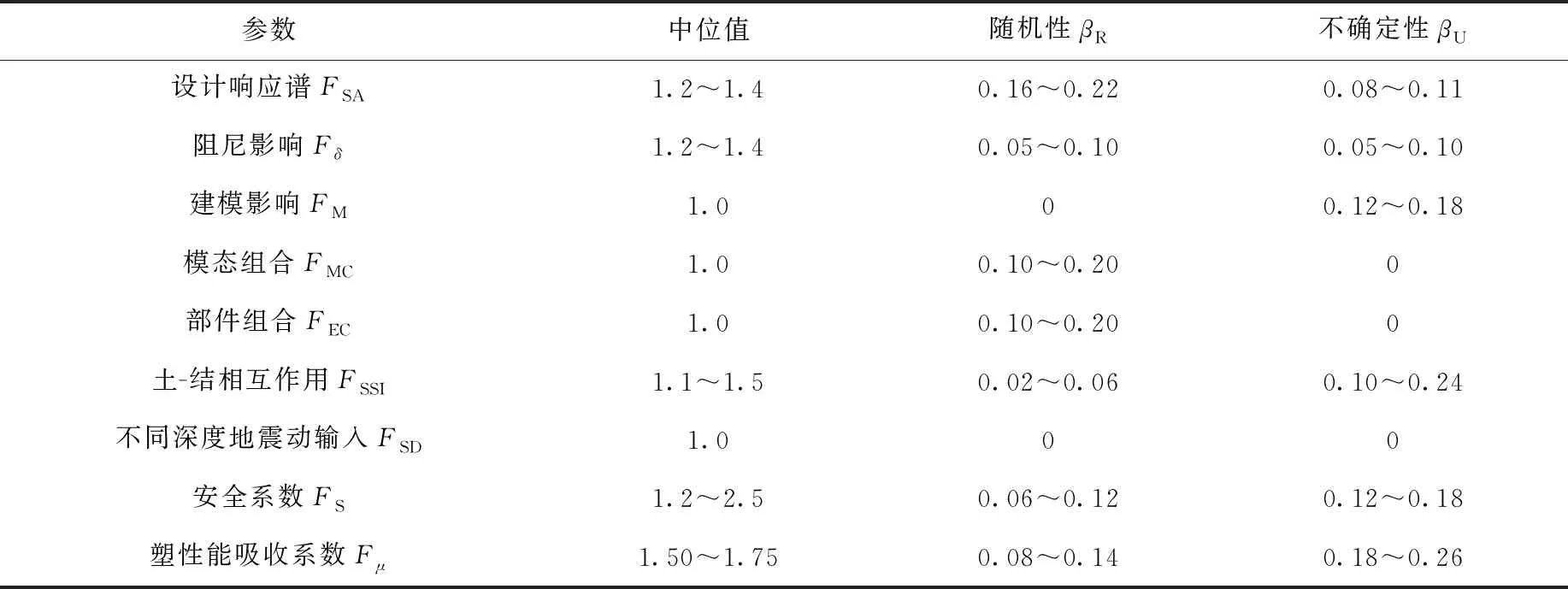
表4 经验地震易损性数据[7,18]

2.4 应用建议

我国已经运行了一些核电厂，由于地震危险性分析技术的进步，已运行核电厂厂址的地震危险性水平可能发生变化。采用解析方法(包括IDA等)生成FS和FSA两个系数(该系数受地震危险性水平影响较大)的解析数据，其他地震危险性水平影响较小的参数采用经验易损性数据，最终得到核电厂安全壳地震易损性曲线。由于地震危险性分析水平进步或实际地震的发生，我国已运行核电厂厂址地震危险性水平可能发生变化，针对上述情况，建议可采用经验-解析数据的地震易损性分析方法初步分析我国核电厂安全壳地震易损性。

3 结论

本文生成了我国某核电厂厂址条件谱，选取了符合厂址危险性的地震动记录，运用IDA方法生成了安全系数FS和FSA的解析易损性数据，连同其他系数的经验易损性数据，采用经验-解析易损性分析方法生成了我国已运行某核电厂安全壳地震易损性曲线，并给出了经验-解析易损性分析方法在我国核电厂安全壳地震易损性中的应用建议，得出以下结论。

1) 条件谱在条件均值谱的基础上，进一步考虑了厂址谱的变化范围，能够表示厂址谱的不确定性。

2) 基于贪心优化算法选取的地震动记录能够匹配场地的危险性。

3) IDA方法可生成地震易损性安全系数法中系数FS和FSA的解析易损性数据。

4) 对于场地危险性变化的核电厂厂址，采用基于混合易损性(经验-解析)数据的地震易损性分析方法可方便生成核电厂安全壳地震易损性曲线。

5) 当我国已运行核电厂厂址地震危险性发生变化时，建议将基于经验-解析数据的地震易损性分析方法应用在我国核电厂安全壳初步地震易损性分析中。