基于CFD程序的物理热工耦合计算不确定性分析

于 涛，雷洲阳，赵鹏程,*，钱冠华，李 捷

(1.南华大学 核科学技术学院，湖南 衡阳 421001；2.南华大学 湖南省数字化反应堆工程技术研究中心，湖南 衡阳 421001)

物理热工耦合方法中的不确定性量化是保障物理热工耦合计算结果可靠性的重要基础，是物理热工耦合的重要研究方向之一。不确定性分析主要采用输入不确定性传播方法，研究输入参数对模型带来的不确定性[1]。将不确定性分析方法应用到物理热工耦合计算，能更精确地预估模型的参数范围，为核反应堆设计、安全分析和评审提供可靠的计算置信区间，具有重要的学术意义和实用价值[2-3]。

国际上，由美国橡树岭国家实验室(ORNL)牵头的轻水堆先进仿真联盟(CASL)于2011年起采用DAKOTA软件开展对多物理耦合的不确定性分析，取得了较为丰富的成果[4-9]；美国能源部(DOE)核能办公室成立的核能先进建模与仿真项目(NEAMS)于2017—2019年采用PROTEUS-Nek5000耦合工具箱SHARP开展了钠冷快堆和铅冷快堆安全特性的不确定性分析研究[10]；欧盟在“欧洲核能技术平台可持续发展(SNETP)”战略规划中开展了NURESIM系列项目，在该项目中基于SALOME平台进行了多物理、多尺度耦合相关研究，并采用URANIE工具箱开展了相关不确定性分析工作[11-13]。近年来，国内也进行了一系列不确定性研究：沈昊等[14]采用敏感性系数法对棒束单相流动传热计算流体力学(CFD)进行了不确定性量化分析；潘昕怿等[15]采用混合法和随机抽样法研究了多群核数据不确定性对堆芯物理计算的影响；高新力等[16]基于SNAP-DAKOTA-RELAP5程序开展了压水堆大破口事故的不确定性分析；张枭羽等[17]采用多项式混沌法进行了压水堆堆芯冷却剂通道计算的不确定性分析；赵阳[18]基于DAKOTA/SALib程序开展了钍基熔盐堆系统事故不确定性分析；曹志伟等[19]采用确定论统计法(GSM)对CPR1000核电厂大破口事故进行了不确定性量化分析；郭炯等[20]基于VSOP-UAM程序开展了高温气冷堆的不确定性分析；刘勇等[21]采用两步法的敏感性计算策略，针对快堆BN-600基准例题的有效增殖因数进行了不确定性量化分析；邓程程等[22]基于RELAP5最佳估算程序对先进热工水力试验(ACME)台架开展了小破口失水事故的不确定性和敏感性分析。一方面，国内在堆物理、系统程序分析不确定性量化方面进行了大量工作，但有关物理热工耦合不确定性分析工作开展较少；另一方面，第4代反应堆中钠冷快堆以及铅基快堆存在极为复杂的物理热工耦合现象，应用不确定性分析可更精确地评估反应堆安全特性，因此有必要进行深入研究。

本文基于CFD程序FLUENT的用户自定义函数(UDF)，耦合中子动力学计算模型、燃料棒热传导计算模型、不确定性分析程序SIMLAB，开发物理热工耦合计算不确定性分析平台CFD/PFS。进而基于CFD/PFS开展小型自然循环铅冷快堆SNCLFR-10的无保护超功率(UTOP)事故不确定性分析，研究燃料多普勒系数等不确定性输入参数对功率峰值等目标参数带来的不确定性，并评估反应性反馈系数对目标参数的影响程度。

1 不确定性分析CFD/PFS平台开发

1.1 点堆中子动力学模型

点堆中子动力学模型(PKM)主要用于计算反应堆内中子密度的动态变化，进而更新堆芯功率，为冷却剂和慢化剂热工水力计算提供热源[23]。本工作采用6组缓发中子的点堆中子动力学模型：

(1)

(2)

其中：N(t)为中子密度；ρ(t)为反应性；Λ为中子代时间；U为缓发中子总份额；t为时间；Ui为第i组缓发中子份额；λi为第i组缓发中子先驱核衰变常量；Ci(t)为第i组缓发中子先驱核浓度；q为外加中子源源强。采用二阶泰勒多项式积分法求解点堆中子动力学方程，将中子密度N(t)使用全隐式二阶泰勒近似展开，以迭代的方式求解不同时刻的中子密度。

点堆中子动力学模型中，中子密度主要由总反应性控制，总反应性包括外部引入反应性和内部反应性反馈[24]。反馈反应性主要包括由燃料温度引起的燃料多普勒反应性、材料密度变化引起的轴向膨胀反应性和径向膨胀反应性以及冷却剂密度反应性。总反应性为：

αc,r(Tc(t)-Tc(0))+αc(Tc(t)-Tc(0))

(3)

其中：KD为多普勒系数；αc,a为堆芯轴向膨胀反馈系数；αc,r为堆芯径向膨胀反馈系数；αc为冷却剂温度反馈系数；Tf(t)和Tc(t)分别为t时刻的燃料、冷却剂平均温度。

1.2 燃料棒热传导模型

燃料棒热传导模型(FTM)包括稳态和瞬态热传导模型，用于求解燃料棒芯块、气隙、包壳的温度，将包壳表面热流密度传递给CFD程序，并反馈PKM燃料芯块和包壳的温度。

1) 稳态热传导模型

芯块热传导：

(4)

气隙热传导：

(5)

包壳内部热传导：

(6)

包壳与冷却剂间的对流换热：

Tcu-Tw=ql/(2π·Rcu·h)

(7)

换热系数h的计算关系式：

(8)

积分热导率[25]：

(9)

其中：Ru为芯块半径；Rci为包壳内半径；Rcu为包壳外半径；T0和Tu分别为芯块中心、外表面温度；Tci和Tcu分别为包壳内、外表面温度；Tw为冷却剂温度；ku、kg、kz、kc依次为芯块、间隙、包壳、冷却剂的热导率；h为包壳与冷却剂间的换热系数；ql为线功率密度；Qv为体积释热率；Nu为努塞尔数；De为当量直径；k(T)为对应材料的热导率公式；k为材料的平均热导率；T为材料温度；Ta、Tb为相邻两节点温度。采用积分热导率法求解燃料棒稳态温度，根据边界条件由外向内迭代求解燃料包壳、芯块的温度分布。

2) 瞬态热传导模型

根据能量守恒，燃料棒瞬态热传导模型的控制方程[26]为：

(10)

忽略燃料棒轴向传热，则：

(11)

(12)

其中：下标m代表材料，包括芯块、气隙、包壳材料；ρm为材料密度；cp,m为材料比定压热容；r为半径；k为材料热导率；i为径向所在的节点数。采用有限差分方法求解燃料棒瞬态导热模型，沿径向将芯块和包壳划分多个节点，迭代求解燃料棒瞬态温度分布。

1.3 计算流体力学模型

CFD模型用于计算冷却剂温度、速度等参数，将冷却剂温度、速度传递给FTM，并反馈PKM冷却剂的温度。CFD模型中的控制方程包括质量守恒方程、动量守恒方程和能量守恒方程，表达式如下。

质量守恒方程：

(13)

动量守恒方程：

(14)

能量守恒方程：

(15)

实际反应堆的几何结构非常复杂，为降低建模难度、节省计算时间，采用多孔介质模型分析堆芯和热交换器模型，将冷却剂流经这些区域的压降等效为动量守恒方程中的附加动量源项[27]，表达式为：

(16)

其中：u为速度矢量；t为时间；ρ为液体密度；ui为速度场分量；μ为湍动能黏度；p为液体压力；xi为方向坐标；Si为外加动力源项；k为流体的热导率；cp为比定压热容；ST为体积热源项；vi为局部流速；μ(T)为随温度变化的流体动力黏度；ρ(T)为随温度变化的流体密度；Di为黏性压降系数；Ci为惯性压降系数。采用有限体积法(FVM)建立离散控制方程组，求解离散方程时选取SIMPLE算法计算流体的温度与速度[28]。

1.4 不确定性分析程序SIMLAB

SIMLAB是由欧洲联合研究中心(JRC)研发的一款不确定性开源程序，具有可视化操作界面，包括统计预处理模块、模型执行模块、统计后处理模块，主要用于不确定性分析和全局敏感性分析[29]。SIMLAB程序在管理经济可行性评估以及模糊推理系统等领域已经开展了不确定性和敏感性分析[30-31]。

SIMLAB程序的统计预处理模块提供参数分布类型及抽样方法，用户根据模型要求选择不同的参数分布及抽样方法。SIMLAB程序中参数分布类型包括正态分布、均匀分布、韦伯分布、指数分布、γ分布、β分布等，也可以自行创建函数关系，且能可视化参数分布。抽样方法主要包括FAST法、Sobol法、拉丁超立方方法、随机抽样法等。

使用非参数统计法(Wilks公式)确定抽样次数，Wilks公式根据分布区间的置信度b及输出参数的概率a确定所需最小抽样数目n[32]。Wilks公式为：

1-an≥b

(17)

(1-an)-n(1-a)an-1≥b

(18)

其中式(17)适用于单侧限值分布，式(18)适用于双侧限值分布。

SIMLAB程序的统计后处理模块用于不确定性分析及敏感性评估。不确定性分析能可视化参数的概率分布、累积分布、逆累积分布，给出参数的均值、方差、标准差、上下限值等统计结果；敏感性评估给出输入参数与输出参数的相关系数或敏感性指数等。

1.5 物理热工耦合不确定性分析平台建立

热工计算包括计算流体力学模型和燃料棒热传导模型，物理计算为点堆中子动力学模型，3个模型的耦合方法如图1所示。PKM进行堆芯中子学计算，对FTM提供堆芯功率；FTM进行瞬态热传导计算，对CFD提供热流密度，对PKM提供燃料温度；CFD进行流动换热计算，对FTM提供冷却剂的温度和速度。

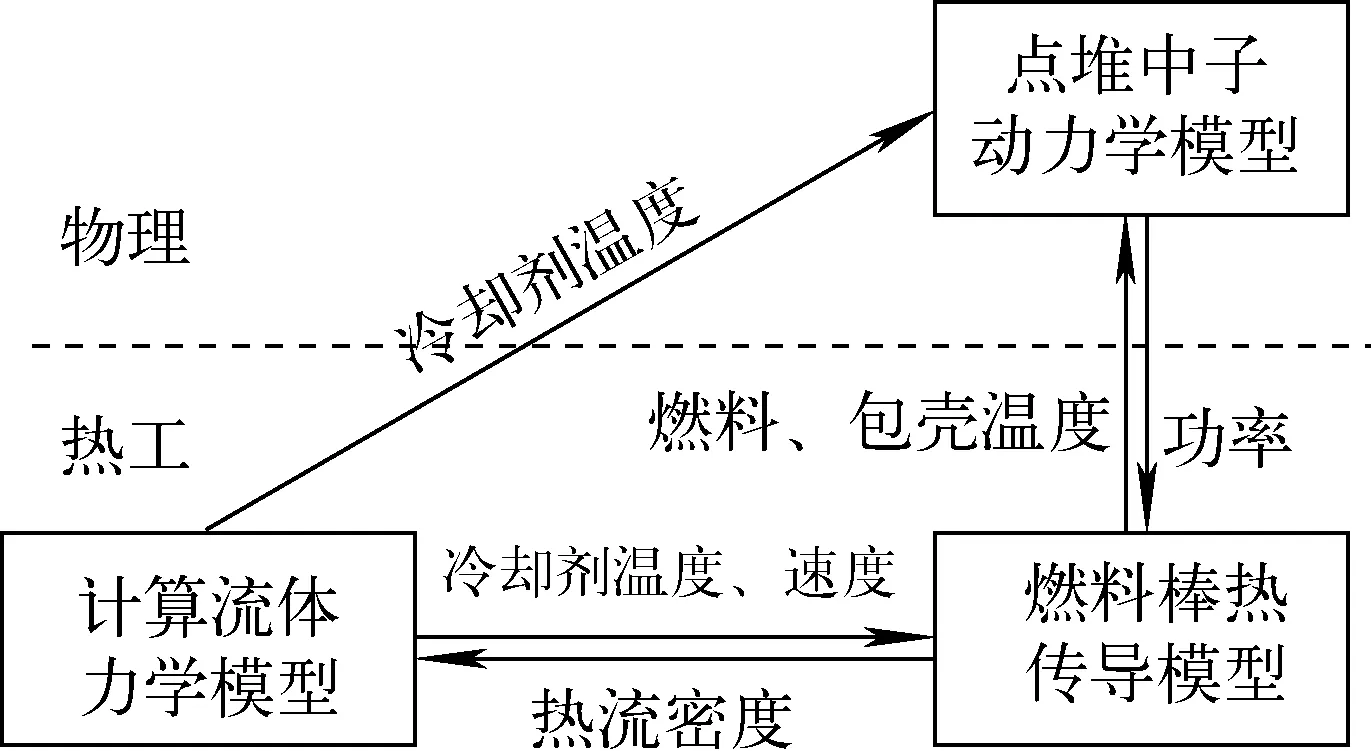
图1 物理热工耦合方法

物理热工耦合程序计算流程如图2所示，首先读取初始、边界条件，调用CFD模块计算稳态的冷却剂温度、速度，将CFD模块计算结果传递给FTM计算燃料棒温度分布，当前后两次计算的各节点温度分布小于0.1 K时，输出稳态计算值；读取稳态计算结果作为瞬态初始参数，将初始化参数传递给PKM计算堆芯功率；FTM通过堆芯功率计算燃料棒温度分布和表面热流密度，CFD模块根据表面热流密度计算冷却剂温度、速度分布；将燃料棒、冷却剂温度分布反馈给PKM用于计算反应性反馈，并将冷却剂温度、速度反馈给FTM。当计算时间达到耦合时间步长，物理与热工模块进行数据传递，之后进行下一时间步的计算，直至FTM计算出的燃料、包壳温度几乎不变，则认为瞬态事故区域稳定，停止计算。

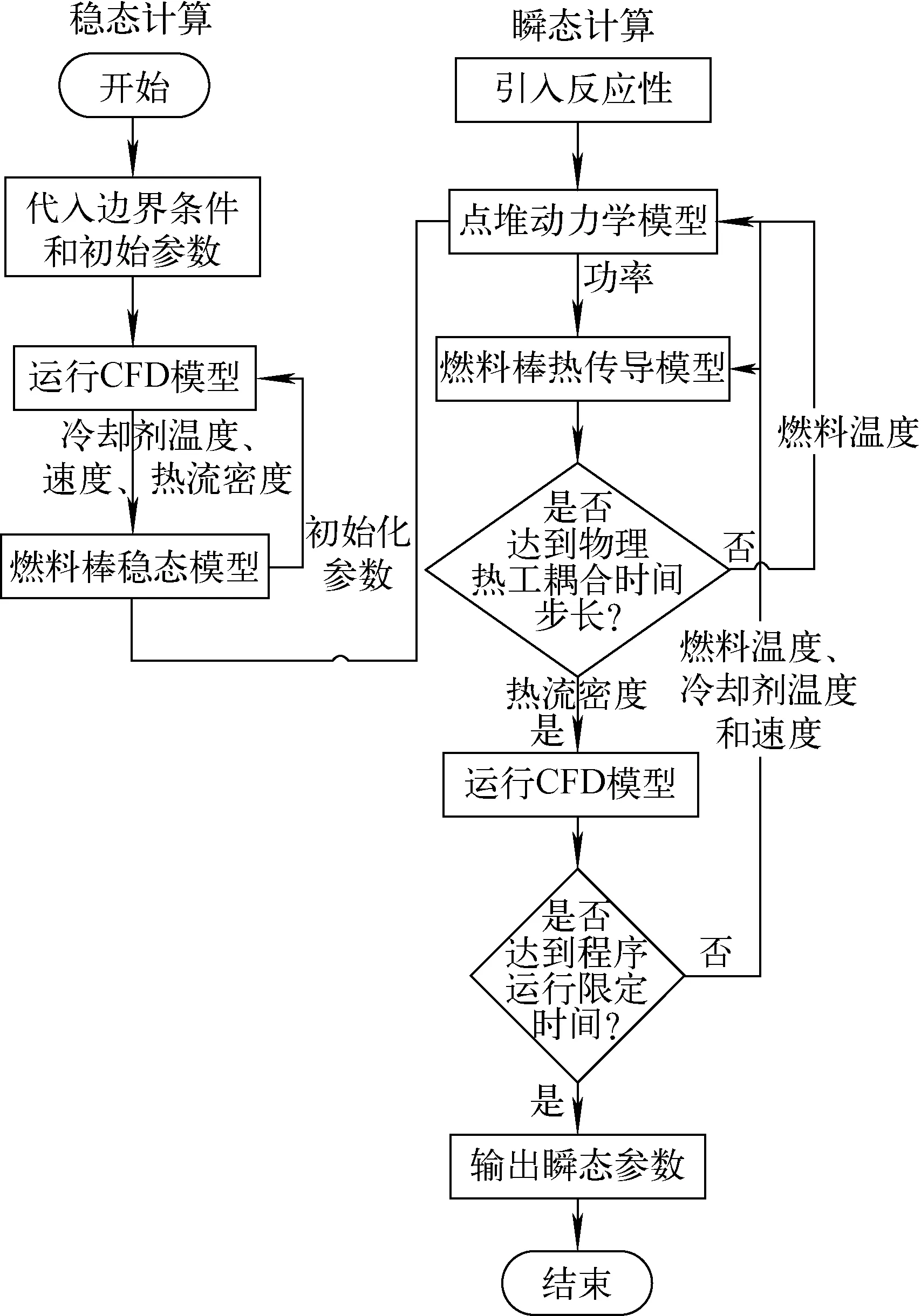
图2 物理热工耦合程序计算流程

通过SIMLAB程序中模型执行模块的外部接口，实现物理热工耦合程序与SIMLAB程序的耦合计算，开发了物理热工耦合不确定性分析平台CFD/PFS。耦合方法如图3所示：通过SIMLAB程序对耦合程序中的不确定性输入参数进行随机抽样，并生成样本文件；将样本文件传递给物理热工耦合程序，经计算获得输出文件；通过执行模块外部接口，将输出文件传递回SIMLAB程序，并应用SIMLAB程序统计分析样本参数与输出参数的相关系数，对参数进行不确定性量化分析。

基于CFD/PFS平台的不确定性计算流程如图4所示，计算流程如下：1) 识别重要的不确定性输入参数；2) 在SIMLAB程序中定义重要输入参数的取值范围及概率分布，选取抽样方法，获得不同的样本组合；3) 将每一组样本组合传递给物理热工耦合程序进行计算获得响应值；4) 将响应值传递给SIMLAB程序，利用SIMLAB程序对结果进行不确定性量化，计算输入参数与响应值的相关系数。

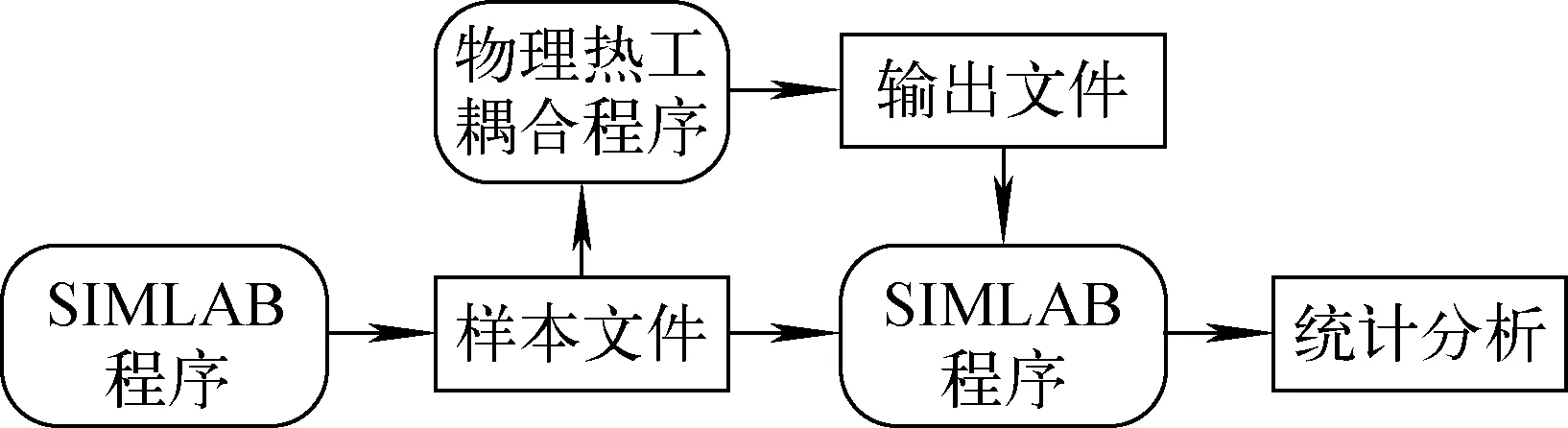
图3 SIMLAB与物理热工耦合程序的耦合方法

图4 不确定性方法的计算流程

2 物理耦合程序验证

2.1 分析模型

小型自然循环铅基快堆(SNCLFR-10)是由中国科学院设计的功率为10 MW的铅铋合金冷却的池式反应堆，燃料采用富集度为19.75%的UO2，燃料包壳采用316L不锈钢，一回路冷却剂采用液态铅铋合金共金体[33]。SNCLFR-10的结构示意图示于图5，堆芯主要设计参数参见文献[34]。采用国际著名快堆多物理耦合分析程序SIMMER-Ⅲ，基于SNCLFR-10无保护超功率(UTOP)事故对CFD/PFS平台物理热工耦合程序开展Code-to-Code验证。

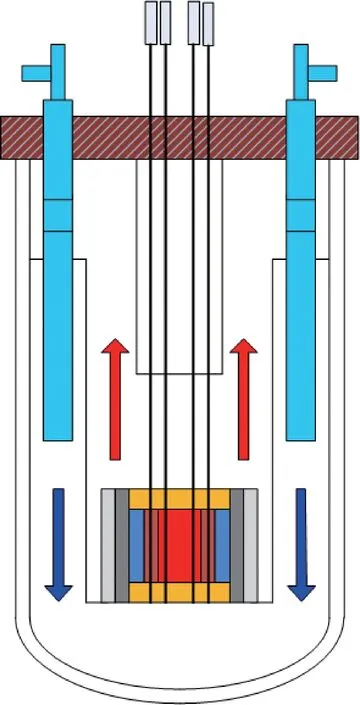
图5 SNCLFR-10的结构

2.2 耦合程序验证

瞬态超功率事故是反应堆设计必须考虑的典型事故瞬态工况，是指向堆内突然引入一个外部反应性，导致功率急剧上升的事故。本文将反应堆初始运行条件设为稳态，在2 s内线性引入1 $反应性，整个瞬态过程无停堆动作。

UTOP事故中反应性的计算值和功率变化如图6所示。反应性在2 s内激增，但由于燃料和冷却剂的负反馈作用，反应性只能提高到0.88 $左右，之后由于燃料和冷却剂的负反馈增大，反应性逐渐降低，反应性最后稳定在临界状态。反应堆功率在2 s内升高30倍左右，由于负反馈作用，功率逐渐降低，最后稳定在58 MW左右。SIMMER-Ⅲ的功率最后稳定在60 MW左右，耦合程序与SIMMER-Ⅲ的相对误差为3.33%。

图7示出燃料最高温度和包壳最高温度随时间的变化。随着功率的增大，燃料最高温度和包壳最高温度逐渐升高，之后随着负反应性的增大，堆芯功率降低，燃料和包壳的最高温度会随之降低。相对于功率的变化，燃料和包壳的最高温度变化幅度较低，其变化在时间上也比功率延迟。耦合程序和SIMMER-Ⅲ计算的燃料最高温度最后分别稳定在2 500 K和2 450 K左右，两者的相对误差为2.04%；包壳最高温度分别稳定在1 098 K和1 080 K左右，两者的相对误差为1.7%。

图6 反应性和堆芯功率随时间的变化

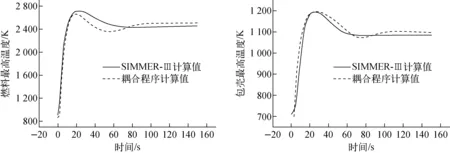
图7 燃料最高温度和包壳最高温度随时间的变化

对比物理热工耦合程序与SIMMER-Ⅲ的计算值，两者的误差较小、符合度较高，说明CFD/PFS平台计算结果具有良好的准确性和可靠性，可用于开展反应堆物理热工耦合不确定性量化分析研究。

3 UTOP事故不确定性分析

3.1 不确定性参数的选取

反应堆中，热工水力反馈参数会通过影响相关核素的核密度或微观截面，从而直接影响组件等效均匀化宏观截面参数，因此将燃料多普勒系数、堆芯轴向膨胀系数、包壳径向膨胀系数和冷却剂温度系数作为不确定性输入参数[35]。为减少抽样取值的偶然性，假设所有输入参数为均匀分布；将输入参数的相对不确定度假设为5%。输入参数的不确定性分布列于表1。

表1 输入参数的不确定性分布

在SNCFLR-10的UTOP事故分析中，将表征反应堆运行状态及安全特性的参数，包括总反应性峰值、功率峰值、燃料及包壳最高温度，选取为不确定性输出参数。

3.2 不确定性量化

选取拉丁超立方方法对输入参数抽样，根据式(18)，满足两个95%双侧限值分布的最小样本量为93。抽取100组工况作为输入样本，为直观检测输入参数的样本量，将输入参数进行归一化处理[36]。假设第i个参数的上限值为Uij，下限值为Lij，第j个样本的参数值为Kij，则归一化结果Xij为：

(19)

Xij的取值在0～1之间，靠近0的样本接近下限值，靠近1的样本接近上限值。

图8示出拉丁超立方抽样样本归一化分布。由图8可见，归一化后的参数服从均匀分布，因此输入参数也服从均匀分布，验证了输入参数抽样的合理性。

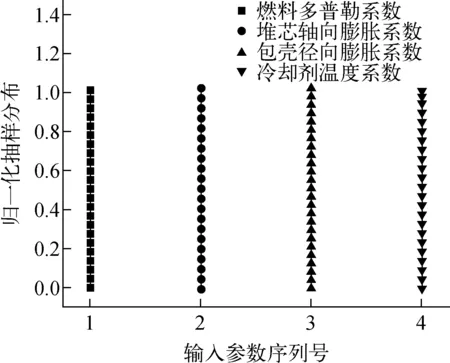
图8 拉丁超立方抽样样本归一化分布

图9示出总反应性峰值、功率峰值、包壳最高温度、燃料最高温度的分布。由图9可知：总反应性峰值的上限值为0.889 13 $，下限值为0.883 89 $，名义值为0.886 63 $，名义值与限值的最大相对偏差为3.09%；功率峰值的上限值为322.2 W，下限值为298.04 W，名义值为310.29 MW，名义值与限值的最大相对偏差为3.948%；燃料最高温度的上限值为2 746.966 K，下限值为2 560.997 K，名义值为2 656.86 K，名义值与限值的最大相对偏差为3.608%；包壳最高温度的上限值为1 221.189 K，下限值为1 169.641 K，名义值为1 196.409 K，名义值与限值的最大相对偏差为2.237%。各目标参数的名义值处于合理的结果不确定性范围之内，表明选取的输入参数分布是合理的；名义值与限值的相对偏差均不超过3.95%，表明计算的目标参数精度较高。

3.3 敏感性分析

输入参数之间的相关性可能影响输入和输出的相关系数，利用偏相关系数(PCC)对计算结果进行分析。偏相关系数表示消除其他影响因素后输入参数对响应值的影响程度，取值在-1～1之间。PCC为0时，输入变量与响应值不相关；PCC为正呈正相关，为负呈负相关；PCC绝对值靠近1时，相关性最强。假设给定随机变量X1和X2作为输入，输出变量Y，在消除X2所产生的影响后，PCC计算表达式为：

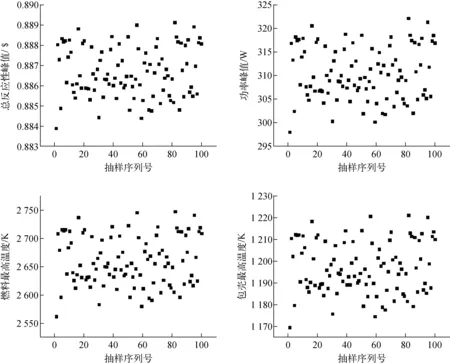
图9 总反应性峰值、功率峰值、燃料最高温度、包壳最高温度的分布

(20)

其中：RX1Y|X2为偏相关系数；RX1Y为X1与Y的简单相关系数；RX1X2为X1与X2的简单相关系数变量间的相关系数；RX2Y为X2与Y的简单相关系数。

图10示出输入参数与响应值的偏相关系数。由图10可见，输入参数与响应值均为正相关，其中，冷却剂温度系数与总反应性峰值、功率峰值、燃料最高温度及包壳最高温度的偏相关系数均小于0.16，属于极弱相关；包壳径向膨胀系数、堆芯轴向膨胀系数与各响应值的偏相关系数在0.4～0.8之间，相关性较强；燃料多普勒系数与各响应值的偏相关系数大于0.94，属于极强相关。

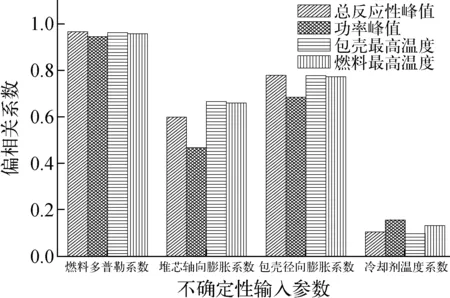
图10 输入参数与响应值的偏相关系数

4 结论

针对物理热工耦合计算进行不确定性分析，能得到更精确的关键参数分布信息，可进一步提高反应堆的安全性。本文介绍了基于CFD程序FLUENT开发的不确定性分析平台CFD/PFS，并采用国际著名快堆多物理耦合分析程序SIMMER-Ⅲ对CFD/PFS平台开展对比验证，进而基于CFD/PFS平台对SNCLFR-10的UTOP事故开展了不确定性分析，并研究了不确定性参数的敏感性，所得结论如下。

1) CFD/PFS平台和SIMMER-Ⅲ程序的事故分析结果吻合良好，所开发的CFD/PFS平台计算结果具有较好的准确性和可靠性，可用于物理热工耦合不确定性量化分析。

2) 通过不确定性分析计算，得到了SNCLFR-10的UTOP事故中总反应性峰值、功率峰值、燃料最高温度及包壳最高温度等瞬态安全参数的95/95双侧容忍限值，且瞬态安全参数的名义值均处于双侧容忍限值内，表明对UTOP事故的不确定性分析具有合理性。量化分析中名义值与限值的相对偏差小于3.95%，表明获得的瞬态安全参数不确定性较小，计算结果精度较高。

3) 对于SNCLFR-10的UTOP事故敏感性分析，通过对4组反应性反馈系数的偏相关系数比较得知，堆芯轴向膨胀系数、包壳径向膨胀系数及燃料多普勒系数对瞬态安全参数的影响较为显著。其中燃料多普勒系数对结果的影响极为强烈，对反应堆安全影响最大。