实钻水平井最优轨道设计技术

李 旭，李锐峰

（大庆钻探工程公司钻井工程技术研究院，黑龙江大庆163413）

近年来，定向井水平井技术随着导向钻井工具的发展而不断进步，从有线测斜仪配合涡轮钻具，到MWD配合弯接头动力钻具（马达）。最近20年旋转导向技术得到了快速发展[1-2]，机械钻速和控制精度不断提高，为复杂油藏特别是非常规油气开发提供了基础[3]。与之相对的是定向井轨道设计，特别是商用的定向井轨道设计软件却在20多年前就已经成熟，可覆盖各类井型。以landmark软件为例，在选定拟合井眼的算法之后（平均角法、平衡正切法、最小曲率法和曲率半径法），当设计者给出部分参数，软件会自动补全其他轨道参数，设计者在此基础上再进行调整得出最终的轨道设计。这种人机交互的试算模式简单易行，且在多数时候能够满足工程需求，但却高度依赖设计者的经验和直觉。而试算出的轨道数据虽然具备技术可行性，却并不一定能保证其最优性。为了更科学地解决这个问题，一些学者把非线性数学规划理论引入到定向井轨道优化设计中，选定目标函数后（轨迹最短），再根据关键参数和各种约束条件的要求建立非线性不等式，应用最优化理论求解[4-5]，也有学者通过特征参数之间的相互验证来解决多样性和优化问题[6]。这些算法实现了最优轨道的定量计算，易于编程实现，但一些关键参数的约束与工程需求和施工特点结合不够紧密，限制了其适用性。根据行业标准，定向井设计原则和井身质量评价如下：满足勘探开发的要求，实现定向钻井目的，设计轨道要经过每个靶点；其次是安全优质快速钻进及采油工艺需求；根据地质设计要求及工程技术条件设计井眼轨道。应尽量选用形状简单、易于施工的轨道。

斜井段的曲率要满足下井管柱的强度要求。保证中靶是水平井设计的首要原则，其次要考虑工程约束并尽量选择简单的轨道剖面。在保证中靶和易于施工的前提下，再优化轨道缩短工程周期。据此，本文选用双弧剖面，并引入非线性数学规划理论对第二增斜段曲率做反推设计提高中靶几率，最后从施工角度选择目标函数对整体轨道做优化处理，提出一种更加贴近工程现场的最优轨道设计。

1 反推设计

1.1 实钻施工风险

水平井中靶离不开对实钻井眼轨道的有效控制，而由于测斜点滞后钻头一段距离（3～16m），因此轨道控制又依赖于对未测井段的造斜率预测。影响预测的因素有很多，主要因素有地质特性、钻具组合结构、井眼轨迹几何形状、钻井工艺参数等，目前尚不能通过数学模型计算做出准确的判断,现场工程技术人员只能通过实钻外推法预测[7]。一旦未测井段地层突变或者造斜工具故障就会造成实钻中未测井段造斜率变化，而工程人员却依然按照之前已测井段的造斜率施工，从而导致实钻轨道偏离待钻设计。以动力钻具配合LWD作为导向工具为例，测点通常滞后钻头12～16m（超过一根钻杆的长度），且一般采用停泵测斜方式，当从测斜数据发觉造斜率突变时，实钻中已经按照已测井段的造斜率定向钻进了两根钻杆的长度，也就是大约19m轨迹数据已经偏离了设计。如果这种情况发生在工程前期，工程技术人员可以有充足的空间调整；但是如果发生在工程后期，实钻轨道偏离设计过大且井底垂深距离靶点垂深已经很近，就容易导致调整之后的剩余井段曲率超标，甚至脱靶。同时，由于地质靶点确定通常是根据临井数据和地震资料估算，存在一定的误差，工程实践中经常会调整靶点垂深且经常是发生在着陆前几十米，如果调整空间不足，同样会造成工程困难和风险。

1.2 轨道设计

要预防以上工程风险，为可能的意外情况预留充分的调整空间，就要从靶点开始反推轨道参数。其中最重要的参数是第二增斜段的曲率，确保出现意外时，调整后的设计在工程条件限制下中靶，也就是调整后的设计曲率（调整曲率）要同时小于下入管柱的曲率上限和工具的最大造斜率的井眼曲率。而意外情况需要按照最严重情况预估，即从测斜数据发现造斜率突变时，19m井段井斜零增长（动力钻具损坏）。如图1所示，第二增斜段的造斜率要保证在设计轨道任意点b，稳斜之后（bc），能够以小于最大调整曲率的曲率中靶。补充说明：根据标准，水平井靶框为上下2m，水平靶区半径按照井型和井深也有相关的标准，轨道只要在靶框范围内就满足中靶。

图1 造斜率图

已知：靶点a垂深Da，靶点井斜αa。第二段圆弧曲率K，工具的最大造斜率形成的井眼曲率Kt，管柱允许最大曲率KP。bc=19m，d点井斜αd=αa，靶区半径为r。

由已知条件：最大调整曲率Km=max（Kt，KP），Rm=5400/(πKm)，Rk=5400/(πK)。轨道上任意一点井斜为αb,则Db=Da-Rk(sinαa-sinαb)，Dc=Db+19cosαb，Dd=Dc+Rm(sinαa-sinαb)；Lb=La-Rk(cosαb-cosαa)，LC=Db+19sinαb，Ld=LC+Rm(cosαb-cosαa)。

根据曲率数学模型计算可以得知，为保证中靶，第二增斜段设计曲率应不大于max（K），稳斜段长度应不小于19m。

2 井眼整体轨道最优设计

图2 双增剖面图

如图2所示，双弧剖面又称“直—增—稳—增—水平”剖面，它是由直井段、第一增斜段、第一稳斜段、第二增斜段和水平段组成，其突出特点是在两个增斜段之间设计了一个稳斜段，用于调整工具造斜率的误差造成的轨道偏移。同时虽然直井防斜打快技术不断进步，但受地层倾角、地层各向异性、工程参数等因素影响，尚不能完全消除坐标偏移[8]，实钻中就不可避免地需要进行方位调整。而无论选择什么导向工具，井眼轨道的控制都需要调整工具面来实现，但工具面角度与井斜和方位的增长只存在定性关系，而不能定量计算，同时精确控制井斜和方位比单独控制一个参数的难度要大得多；在需要全力增斜井段如果兼顾方位，还会削弱增斜效果。因此，为降低第二增斜段的控制难度增加中靶几率，需要进入第二增斜段之前把方位调整至靶点方位，保证第二增斜段只需做增斜控制。

如图3所示，坐标偏移时工程中调整方位最容易实现的方法是在第一增斜段开始保持方位不变，以一定的角度不断贴近设计闭合方位线，在稳斜端末段把方位调整至靶点方位，这样就避免了对井斜和方位同时进行调整，降低了工程难度。从施工角度，减少方位变化θ，可以提高轨道平滑度，方便后续施工；还可以缩短钻井周期。由于导向马达、随钻测量系统构成的滑动钻井仍然是目前的主要定向钻井方式[9]，在滑动钻进过程中，钻柱不发生旋转运动，通过滑动导向工具改变井眼的井斜角和方位角[10]，而滑动钻进时钻柱带来的静擦阻力降低了实际施加在钻头上的钻压，而为了保持工具稳定保证定向效果很多时候施加的钻压不能太大，导致滑动钻进速度远低于旋转复合钻进，因此通过减少方位θ变化来减少滑动钻进进尺，就可以缩短了钻井周期。而方位变化θ的大小由坐标偏移量与第一造斜段和稳斜端的水平位移共同决定（其中坐标偏移量是不可控因素），增加第一造斜段和稳斜端的水平位移可有效减小θ。据此，本文选择稳斜末的水平位移作为目标函数。

3 结论及认识

涉及水平井井眼轨道设计与轨迹计算的技术方法很多，笔者认为要满足实际施工需求为宗旨。本文把中靶作为目标函数，在此基础上尽量减少定向井段以减少施工周期，可以取得较好的实钻效果。

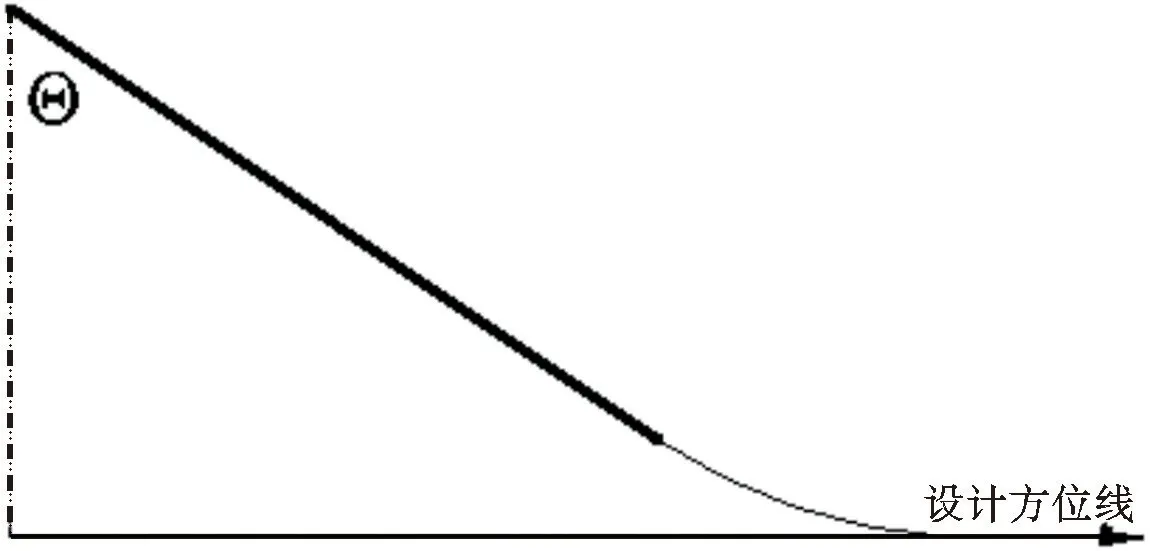
图3 坐标偏移时第一增斜段和稳斜端水平投影