基于RBF神经网络和遗传算法的ERT传感器优化*
颜 华,张 馨,王伊凡
(沈阳工业大学 信息科学与工程学院,沈阳 110870)
电阻层析成像(electrical resistance tomography,ERT)是电学层析成像的一种,可用于封闭的管道或容器内两相流或多相流的可视化测量,具有非侵入、成本低、响应快及无辐射等优点,在石油、化工、生物医学、农业和食品等领域有广阔的开发和应用前景[1-4],是目前过程层析成像技术研究的一个热点.ERT系统由传感器、投影数据采集系统和图像重建计算机三部分组成.传感器的电极阵列由一系列等间隔排布在管道或容器内部的电极组成.系统通常采用相邻激励、相邻测量的工作模式,即以一对相邻电极为激励电极,注入电流建立敏感场,测量激励电极对以外的相邻电极对上的电压,获取不同方向上的物场信息,再采用适当的重建算法重建出被测区域的电导率分布.
ERT传感器的结构参数对敏感场特性以及整个ERT系统性能有重要影响.通过传感器的优化设计提高传感器性能指标具有重要意义.由于无法获得目标函数与结构参数间的解析关系,优化设计通常采用正交试验或智能优化算法实现.Wang等[5]通过指标综合满意度对多指标正交试验中ERT传感器各性能指标进行模糊分析,将多指标正交试验问题转化为单一指标的正交试验问题,进行了电极高度、宽度和数目的优化;肖理庆等[6]以灵敏度矩阵条件数的倒数为适应度函数,利用改进粒子群算法优化了ERT阵列电极的宽度;孙启国等[7]建立了油气润滑测试系统中的电容层析成像传感器的有限元模型,利用敏感场的均匀性、电容极值比和电容平均差值构成传感器综合优化函数,用正交试验的方法优化了基准ERT传感器的轴向保护环长度和间距.
与单指标的优化设计法相比,以多指标综合评价为优化目标的传感器优化会收到更好的效果.重建图像误差与被测介质分布有关,不能“纯粹”地反映传感器本身的固有特性.选择对成像质量有较大影响,且与被测介质分布无关的多个性能指标构成优化目标,可使优化后的传感器具有更好的介质分布适应能力.基于以上考虑,本文采用能反映传感器固有特性的敏感场均匀性和灵敏度矩阵条件数构成传感器性能的综合评价指标,提出一种RBF神经网络与遗传算法相结合的传感器参数自动寻优方法.
1 优化参数确定
ERT传感器参数包括电极数目、电极长度、电极宽度、管壁材质、电极材质及工作模式等.ERT传感器优化通常是在给定ERT数据采集系统的前提下进行的,采集系统确定后,传感器的电极数目、工作模式皆已确定.
现有ERT系统的数据采集通道数为16,电极宽度为8 mm,电极长度为7.85 mm,工作模式为相邻激励、相邻测量.所采用的绝缘管道内径为50 mm、外径为55 mm,管壁材质为有机玻璃.由于电极紧贴管壁内侧,因此可忽略管壁材质及厚度对传感器性能的影响.电极材质的选择主要依据物理特性,钛的耐蚀性好、强度、塑性、韧性均较好,故采用钛电极.在COMSOL中建立图1所示的16电极ERT传感器模型,待优化参数为电极宽度d和长度h.
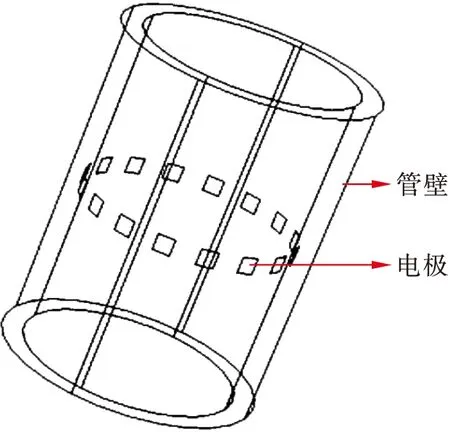
图1 ERT传感器结构Fig.1 Structure of ERT sensor
2 传感器参数对传感器性能的影响
2.1 常用的传感器性能评价指标
ERT传感器的性能可以用灵敏度矩阵条件数、敏感场均匀性、响应电压范围、响应电压最小值、重建图像误差等指标来评价.
由于逆问题的不适定性,ERT传感器的灵敏度矩阵病态严重,给高质量图像重建带来很大困难.灵敏度矩阵条件数(C)可定义为矩阵的最大奇异值与最小奇异值之比,该值越大,矩阵越接近奇异,病态越严重.
ERT的敏感场是极不均匀的,管道中心区域灵敏度远低于管壁附近的灵敏度,这会导致中心区域的重建质量较低.敏感场的均匀性可以用敏感场均匀性(P)来评价,即
(1)
(2)
(3)

2.2 电极宽度与长度对传感器性能的影响
研究电极宽度对传感器性能影响时,电极长度固定为8 mm(原长).由于16个电极设置在内径为100 mm的管道内壁,故电极宽度d的取值范围为0 mm 图2 电板宽度对均匀性、条件数和响应电压的影响Fig.2 Influence of electroplate width on uniformity,condition number and response voltage 图3 电板长度对均匀性、条件数和响应电压的影响Fig.3 Influence of electroplate length on uniformity,condition number and response voltage 由图2可以看出:敏感场的均匀性会随着电极宽度的增加而有所改善,但为获得较小的灵敏度矩阵条件数和较小的测量电压范围,电极宽度不能过宽.由图3可以看出:敏感场的均匀性会随着电极长度的增加而变差,但灵敏度矩阵的条件数和响应电压范围却随着电极长度的增加而显著降低.综上电极的宽度和长度取值不宜过大或过小,为此设定它们的取值范围分别为1.96 mm 由2.2节可知,电极长度、宽度与敏感场均匀性、灵敏度矩阵条件数之间存在着复杂的非线性关系,且难以建立确切的解析式.RBF网络[8-9]能够逼近任意的非线性函数,可以处理系统内在的难以解析的规律性,不存在局部最小问题,且具有良好的泛化能力和极快的学习收敛速度.为此本文采用RBF神经网络建立回归模型,所采用的RBF神经网络输入有两个神经元,分别对应h、d;输出有两个神经元,分别对应P和C;隐含层神经元数目为30. 给定h、d,利用COMSOL可以获得相应的P和C,构成一组样本数据.采用这种方式构成163组样本数据,并分别采用数据中P和C的最大值对组中的P和C进行归一化处理.取150组样本数据用于神经网络训练,13组样本数据用于考察模型的泛化能力与拟合精度. 图4给出13组样本数据所对应的真实值和预测值.决定系数R2表示神经网络模型对观测值的拟合程度,P和C所对应的R2分别为0.923 27、0.937 91,拟合效果较好. 图4 神经网络回归模型预测Fig.4 Prediction with neural network regression model 本文用灵敏度矩阵条件数C和敏感场均匀性P构成传感器综合评价指标F,并确定优化目标函数为 minF=a1C+a2P (4) 式中,a1、a2为决定各个因素对F值影响的大小变量,可根据优化侧重点不同进行相应调整,本文选取的值为a1=5,a2=1.灵敏度矩阵条件数反映逆问题病态的严重程度,对重建质量有很大影响,故对它赋予了较大的权重.这里给出的权重值是在尝试了多组权重值后通过典型分布的重建效果而确定的. ERT数据采集系统都有较大的输入信号范围,故本文没有把响应电压指标纳入优化目标,只是在设定电极长度和宽度的取值范围时,保证对应的响应电压在数据采集系统的允许区间. 遗传算法是一种进化算法,其基本原理是仿效生物界中的“物竞天择,适者生存”的演化法则,迭代出最佳近似解.遗传算法不依赖于问题的具体领域,对问题的种类有很强的鲁棒性,固有的并行计算能力使其在求解过程中具有较好的全局搜索性能和快速的收敛性[10-11].本文采用遗传算法进行参数寻优. 目标函数为最小值问题,本文采用Ranking函数计算个体的适应度值,即先用RBF神经网络计算出个体所对应的目标函数值,按照目标函数值由大到小的顺序对个体排序,然后根据每个个体在排序中的位置(e)计算出个体的适应度函数,即 (5) 式中:p为压差值,本文取值2;W为种群中所包含的个体数目,本文取值10,即10组h、d,寻优范围为h∈(1 mm,36 mm),d∈(1.96 mm,17.67 mm).在每代中,通过RBF神经网络回归模型,计算出h、d对应的C与P,再根据个体的适应度大小选择个体,借助于自然遗传学的遗传算子进行组合交叉和变异,产生代表新的解集的种群.本文的代沟值取20,用于控制每代中种群被替换的比例;交叉值取0.7,表示染色体中元素交叉的概率大小;变异值为0.5,表示染色体中每一个元素变异的概率大小;最大遗传代数为100.达到迭代终止条件后,末代种群中的最优个体,经过解码之后作为最优近似解,即电极最佳长、宽值. 本文经100次迭代寻优后,得到的优化参数为:d=8.504 mm,h=30.055 mm.图5给出了遗传算法迭代寻优过程中目标函数值F、灵敏度矩阵条件数C和敏感场均匀性P随迭代次数的变化曲线.其中解的目标函数值(解的条件数、解的均匀性)是指每一代种群中最佳h、d值所对应的目标函数值(条件数、均匀性),种群平均目标函数值(种群平均条件数、种群平均均匀性)是指每一代种群中所包含的10组h、d值所对应的目标函数值(条件数、均匀性)的平均值. 图5 目标函数值、条件数和均匀性的变化曲线Fig.5 Changing curves of objective function value, condition number and uniformity 由图5可以看出:1)整个迭代过程中保证了种群具有多样性;2)随着迭代次数的增加,每一代的最优F值、C值和P值均能迅速减少并达到稳定. 为检验优化效果,首先比较了优化前、后的传感器的性能指标,如表1所示. 表1 传感器性能指标Tab.1 Performance indexes of sensor 为进一步检验优化效果,分别采用优化前、后的传感器对5种典型流型分布进行了仿真数据重建.重建时均采用了文献[12]提出的改进Landweber重建算法.表2给出了实际分布和重建分布比较结果.表2中的实际分布是用COMSOL建立的有限元仿真模型,重建分布是用ERT传感器输出的有限元仿真值和Landweber重建算法获得的分布.表3给出了用相关系数DC、空间误差SIE和相对图像误差RE评价的重建质量.式(6)~(8)给出了DC、SIE和RE的定义,即 (6) (7) (8) 由表2、3可以看出:传感器优化后,其综合评价指标、重建图像的视觉效果以及重建图像误差均有明显改善. 本文建立了以电极长度h、电极宽度d为输入,敏感场均匀性P、灵敏度矩阵条件数C为输出的RBF神经网络回归模型,实现了传感器参数与传感器性能指标间复杂的非线性关系.用P和C形成传感器综合评价指标F,并以最小化F为目标函数,用RBF神经网络计算个体的适应度函数,实现了传感器结构参数的自动寻优. 表2 实际分布与重建分布Tab.2 Real and reconstructed distribution 表3 重建图像误差Tab.3 Reconstructed image errors 需要指出的是本文给出的是一种ERT传感器优化设计方法,而不是一套ERT传感器结构参数.当被测对象(比如输送管道的直径)发生改变时,可采用本文方法对ERT传感器结构参数重新进行优化.优化时可根据优化的侧重点选取若干传感器指标构成综合评价指标,并对这些指标赋予适当的权重.

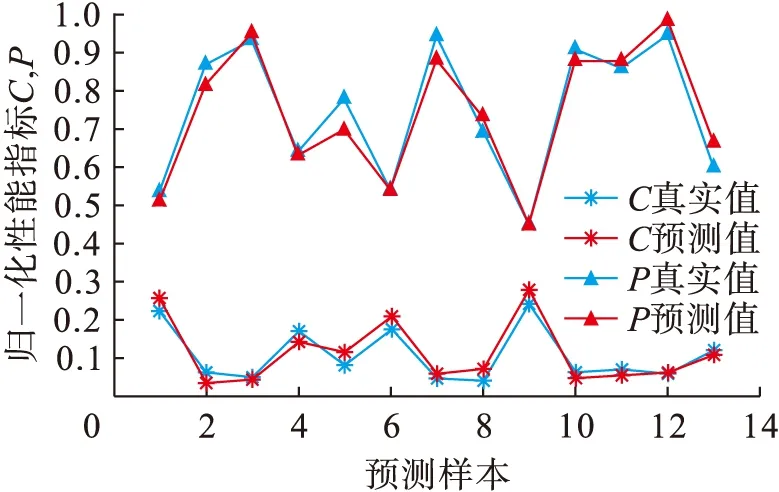
3 神经网络回归模型建立
4 基于遗传算法的传感器优化
4.1 优化目标的确定
4.2 遗传优化算法

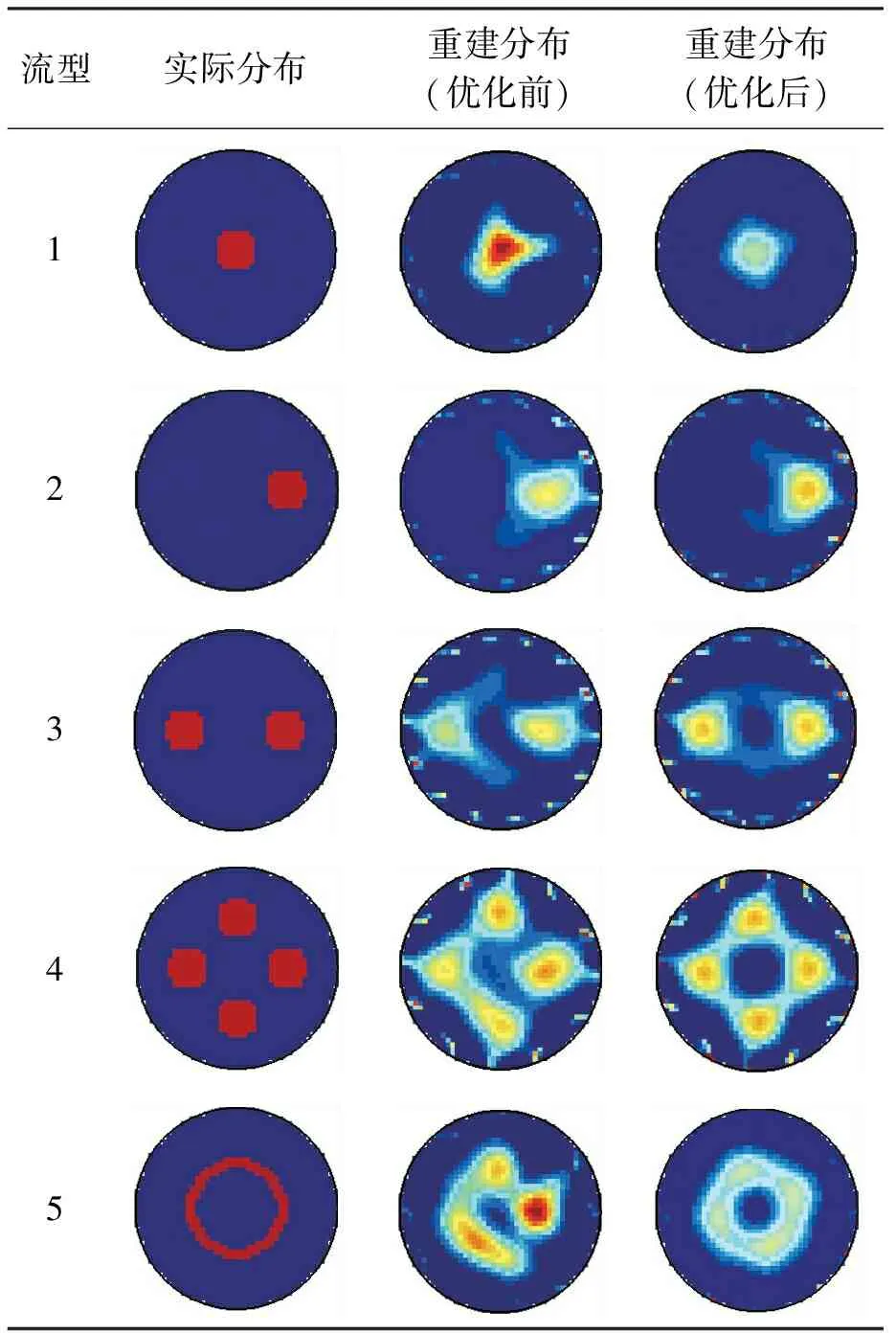
5 ERT传感器优化效果检验

6 结 论