基于改进Elman神经网络的变压器故障诊断方法*

王英洁，曹铁男

(中国南方电网有限责任公司 科学研究院，广州 510663)

电力变压器作为电力系统的重要组成部分，其运行状态对整个电网的运行起着至关重要的作用.变压器在运行过程中通常会受到热应力、过载、绝缘材料老化、外部环境变化等因素的影响，从而产生故障，因此，及时对变压器进行故障诊断是检测变压器故障、保证变压器正常运行的重要措施，是维护电网安全运行的必要保证[1].

变压器实行状态监测过程中，一般会获得大量的监测数据，同时这些数据呈现显著的多样性，反映了相应的变压器状态信息，而这些状态信息可以从不同方面表征电力变压器的运行状态.采集变压器的状态监测数据，并对数据中所包含能够反映变压器运行状态的状态信息进行有效分析，这对于提高变压器状态评估的准确性具有重要意义[2-3].目前，对于变压器的故障诊断主要采用油中溶解气体分析(dissolved gas analysis，DGA)，通常利用三比值法对油中溶解气体进行分析，但该方法存在编码不完全、编码边界过于绝对等缺点.随着信息技术与人工智能的发展，新的电力变压器故障诊断技术不断被提出，其包括：人工神经网络[4-5]、贝叶斯网络[6-7]、聚类分析和模糊理论[8-9].Miranda等[5]采用均值漂移法生成虚拟数据，增加神经网络训练样本，提高变压器故障诊断的准确性；白翠粉等[7]通过分析非理想工作条件、故障模式和异常状态的因果关系，建立了三级贝叶斯网络模型；Izakian等[8]提出了用固定长度的滑动窗口生成一组序列，并用模糊c均值聚类方法分析序列中的结构，找出序列中的异常；裴玉龙等[9]建立分级评价指标体系，引入均衡函数的变权模型.

根据当前变压器故障诊断的研究现状可以看出，变压器异常运行状态分析仍是目前研究的重点方向.单纯地将DGA特征气体作为故障诊断时，故障特征的输入向量过于单一，导致众多重要的状态监测信息未得到合理利用.本文提出一种基于Elman神经网络的变压器故障诊断方法.首先将核主成分分析方法应用于Elman神经网络，实现选取参数的降维，并提取出主要特征参数；然后将其作为Elman神经网络的输入变量，对Elman神经网络进行训练；最后将收集到的数据集作为测试集导入完成训练的Elman神经网络中，再进行相应的诊断测试.试验结果表明，基于Elman神经网络的变压器故障诊断方法与支持向量机和BP神经网络相比，具有更高的诊断精度.同时随着收集到的样本数据量的提升，神经网络诊断的正确率也随之增加.

1 核主成分分析

主成分分析法是从高维变量中，提取低维少量成分的线性降维方法.尽管方法减少了数据的维数与复杂度，但提取得到的特征量仅能表征设备状态的线性成分，从而丢失了原始数据序列中的非线性成分与相应的有效信息.核主成分分析法在主成分分析法的基础上，利用核函数将原始数据映射到高维线性特征空间，然后利用主成分分析法进行特征提取.核主成分分析法的实质是分析映射到特征空间的数据[10].

设原始数据为x={xij}m×n，非线性映射函数Φ将原始数据x映射到特征空间F，在特征空间F中原始数据第i个样本xi以Φ(xi)进行表征，然后即可采用主成分分析法提取数据的主成分.

当映射后的数据Φ(xi)平均值为0时，高维特征空间F上的样本协方差矩阵为

(1)

用v作为式(1)中样本协方差矩阵特征值的特征向量，则可得到

Cv=λv

(2)

在式(2)两边同时乘以Φ(xk)，则有

Φ(xk)Cv=λ(Φ(xk)v)

(3)

由于特征向量v可以由数据集Φ(xi)线性表示，则令βi作为相关系数可得到

(4)

将式(1)与式(4)代入式(3)可得

(5)

定义m×m维的核方差矩阵为

K=Φ(xi)Φ(xj)

(6)

为了保证输入数据Φ(xi)满足高维映射所需要的平均值为0的条件，需要修改核方差矩阵K，修改后的核函数为

(7)

式中，Im为m阶值为1的矩阵.计算特征值与特征向量，然后对特征值进行排序，并适当地调整相应的特征向量，最后对特征值的累积贡献率Ck进行相应的累加计算.在计算累积贡献率的过程中，可以根据变压器型号参数等实际情况对相应的阈值ε进行设定.若Ck>ε，则选择序列k作为主元素.

2 变压器故障诊断方法

2.1 改进Elman神经网络

Elman神经网络[11]可以通过延迟与存储连接层使得隐藏层的输出端连接对象变为自身的输入端，由此可以使Elman神经网络在对历史数据进行遍历时，具备较好的灵敏度.同时，Elman神经网络的内部反馈结构能够较大程度上增强自身处理动态变化信息的性能，从而实现动态化构建模型的目标.此外，Elman神经网络还能够忽略外部噪声在某些情况下存在的特定形式.若给出正确的输入与输出，则可以针对整个监测系统使用Elman神经网络建立故障诊断模型，从而实现变压器的故障诊断.

本文利用核主成分分析方法对选取的参数进行降维，并提取出主要特征参数作为Elman神经网络的输入变量，然后对映射到Elman神经网络特征空间的数据进行分析，实现对Elman神经网络的改进.由此得到的Elman神经网络的特征空间便为非最小状态空间，即

Y(k)=G(ω3z(k))

(8)

z(k)=F(ω1zc(k))+ω2(u(k-1))

(9)

zc(k)=z(k-1)

(10)

式中：Y为m维输出量；G为输出神经元的传递函数；z为n维中间层量；zc为n维反馈量；F为中间层神经元的传递函数；u为r维输入量；ω3为中间层与输出层之间的链接权重；ω2为输入层与中间层之间的链接权重；ω1为连接层与输出层之间的链接权重.根据多位学者对于Elman神经网络的相关研究与探索，当初始的各层链接权重取值为-0.3～0.3之间的随机数能够较好地确保Elman神经网络模型的训练效果[12-13]，因此本文在仿真时将初始的各层链接权重取值为-0.3～0.3间的随机数，通过设定目标函数不断修改各层链接权重.

在Elman神经网络中修改权重时，误差平方和函数可以用作学习目标函数，为了确保诊断准确率，将设定的目标误差平方和限定为0.000 1.

2.2 变压器故障诊断流程

使用改进Elman神经网络的变压器故障诊断的流程如下：

1) 采集变压器在线监测数据，计算油中气体浓度比，包括IEC比值、Rogers比值和Dornenburg比值等，合计20个参数，将其分为特征气体、气体浓度比和变压器特征参数三类，其中特征气体有7个：H2、CO、、CO2、CH4、C2H2、C2H4及C2H6；气体浓度比有6个：CH4/H2、C2H2/C2H4、C2H4/C2H6、C2H6/CH4、C2H2/CH4及C2H6/C2H2；变压器特征参数有7个：总烃类绝缘油的介电损耗、体积电阻率、极化指数、铁芯绝缘电阻、铁芯接地电流、局部放电量和变压器振动信号.

2) 将采集到的变压器数据划分为训练集和测试集，并将其标准化，使数据确保在0～1范围内.

3) 利用核主成分分析算法得到高维特征空间核方差矩阵的特征值和相应的特征向量，然后计算特征值的累积贡献率.将累积贡献率由高到低进行排序，选取其中累积贡献率在90%以上的特征值对应的特征向量作为主要特征向量来表征原始数据包含的主要状态信息.

4) 将主要特征向量作为Elman神经网络的输入，输出为变压器6种故障类型.变压器常见的6种故障类型为：局部放电、低能放电、高能放电、轻度热故障(T<300 ℃)、中度热故障(300 ℃≤T≤700 ℃)和重度热故障(T>700 ℃).

5) 在神经网络中测试收集到的测试集数据，进而对变压器不同故障类型进行诊断.

3 试验分析

本文收集的数据来自：变压器在线监测数据、变压器离线试验数据、变压器历史故障数据和相关参考文献，总共收集了311个案例[14-15].随机选择所有案例中共计200组数据作为测试样本，每组数据中包含故障变压器的特征气体、气体浓度比和变压器特征参数三类共20个参数，并计算各参数的贡献率.贡献率排序后的结果如图1所示.序号为1～9参数的累计贡献为98.2%，已达到设定要求，因此，选择序号为1～9的参数作为训练Elman神经网络的主要特征参数.

图1 参数贡献率Fig.1 Contribution rate of parameters

表1给出了基于改进Elman神经网络的变压器故障诊断方法的诊断情况.主要对比在变压器故障类型不同、样本集数量不同，以及使用训练集和测试集情况时诊断方法的准确性.由表1可以看出，本文所提出的诊断方法在应用于训练集与测试集时的准确性有所不同，测试集的诊断准确率基本均低于训练集.当样本容量达到较大数值如200时，训练集和测试集的诊断准确率均超过了80%，诊断的准确率较高.本文所提出的诊断方法与样本容量有关，当样本容量为100时，面对变压器不同故障类型，无论是训练集还是测试集，方法诊断准确率普遍低于70%；而随着样本集数量增加，方法的诊断准确率不断提升，当样本数量为250时，训练集的诊断准确率均高于90%，测试集的诊断准确率均高于85%.可以看出，在面对不同故障类型时，当样本容量达到一定的数量水平时，本文所提出的诊断方法具有较高的诊断准确率.

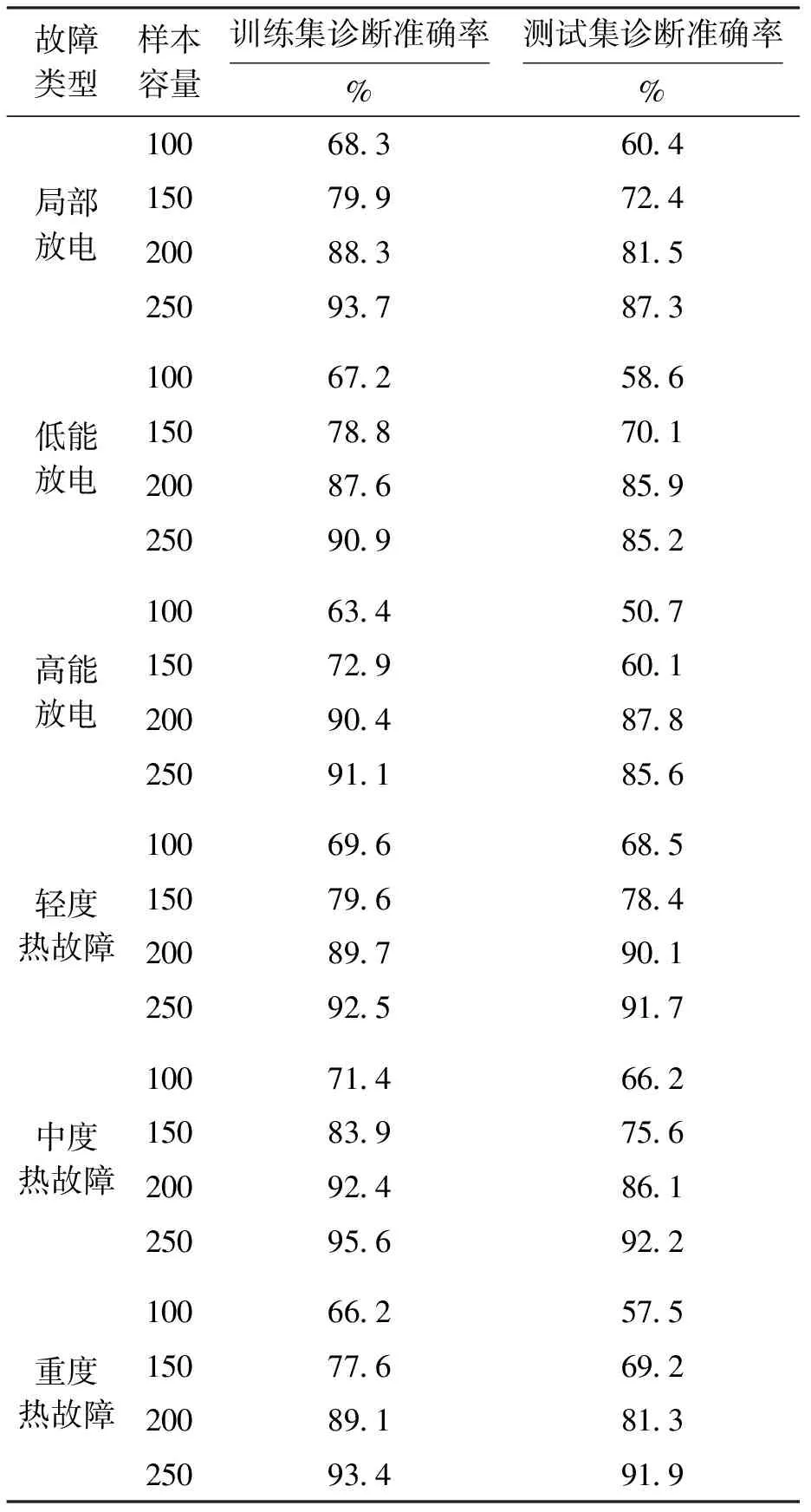
表1 诊断方法准确率对比Tab.1 Accuracy comparisonof diagnostic methods

将采用核主成分分析法得到的特征参数与采用IEC比值、Rogers比值和Dornenburg比值得到的特征参数分别输入Elman神经网络，对故障进行诊断并将结果进行对比.表2给出了上述几种特征参数输入Elman神经网络后的故障诊断准确率的对比情况.训练集和测试集样本容量均为200，诊断故障类型为重度热故障.由表2可以看出，与其他方法相比，使用核主成分分析法提取得到的特征参数有助于提高Elman神经网络的诊断准确性.

将本文所提出的基于改进Elman神经网络的变压器故障诊断方法与BP神经网络和支持向量机(SVM)的故障诊断方法进行对比，训练集和测试集样本容量均为200.其中，BP神经网络采用5层网络结构模型，包括：输入层、3个隐藏层和输出层.对于支持向量机(SVM)，文中使用基本模型，其训练集也为200.表3给出了针对不同故障类型时不同诊断方法的诊断准确率对比结果.由表3可以看出，BP神经网络和SVM的故障诊断准确率大多均低于80%.与BP神经网络和SVM相比，本文所提出的基于改进Elman神经网络的变压器故障诊断方法诊断准确率均普遍高于80%，具有更优的诊断精度.

表2 不同特征参数诊断准确率Tab.2 Diagnostic accuracy under different characteristic parameters %

表3 不同诊断方法诊断准确率Tab.3 Diagnostic accuracy of different methods %

4 结 论

本文提出了一种基于改进Elman神经网络的变压器故障诊断方法，利用核主成分分析方法对参数进行降维提取，使得可供分析的参数增多.将提取到的特征参数按照累积贡献率进行排序、筛选，然后输入Elman神经网络，实现在考虑多参数条件下对变压器故障的诊断.该方法有助于解决变压器故障诊断精度低、可分析参数少的问题，同时对变压器故障的诊断准确率较高，可提升电力系统运行的安全性和可靠性.

由于样本数据仍相对较小，所以程序的运行时间较短，进而需要考虑当样本数量相对较大时，是否能够快速获得故障诊断结果.未来研究将在样本容量较大的基础上进一步完善该变压器故障诊断方法，并基于大数据样本研究多类型电力设备故障诊断方法.