基于低温启动特性的PEMFC水热性能仿真与分析＊

许德超 赵子亮 盛夏 赵洪辉 王宇鹏

（1.中国第一汽车股份有限公司研发总院，长春 130013；2.汽车振动噪声与安全控制综合技术国家重点实验室，长春 130013）

主题词：质子交换膜燃料电池 冷启动 水伴热值 产水速率

1 前言

质子交换膜燃料电池（Proton Exchange Membrane Fuel Cell，PEMFC）因其高效率、高功率密度以及响应快速等特性被认为是在汽车领域最具应用潜力的燃料电池技术之一[1]。目前，影响燃料电池汽车发展的主要障碍包括加氢基础设施不完善、成本较高和在极寒区域无法使用。在寒冷地区使用受限主要是因为燃料电池冷启动问题[2]，即电堆在0 ℃以下启动时，电极反应产生的水在排出电堆前结冰，并进一步导致膜电阻上升、反应物传质通道堵塞以及反应位置被冰层掩盖等情况，最终导致冷启动失败，甚至性能退化。冷启动性能的影响因素主要包括电池子部件的材料特性、单体及电堆的结构设计、启动模式和加载控制策略。水在电池内的结冰会对膜电极组件（Membrane Electrode Assembly，MEA）造成破坏，因此在电池升温到0 ℃之前控制液态水含量保持在最小值附近是一种合理的思路[3]。

电堆通过自身反应升温（自热）实现冷启动时，需要保证其内部不结冰或者尽量少结冰，以避免可能引起的性能衰减。在电堆自热升温期间，其是否结冰以及结冰量显然与自热过程中生成的水量相关，而水生成量与电流成正比。此外，电流又与发热功率相关，因此，控制电堆的水生成量，并最大化内部发热功率成为自热冷启动成功的核心。

为了更好地说明上述相关性，本文引入水伴热值的概念，即生成单位质量水所产生的热量，并进行3D仿真计算，以期为冷启动控制策略的制定提供参考。

2 仿真模型描述

2.1 模型说明

本文采用多物理场仿真软件Comsol 5.4 进行建模计算。在模型中主要求解的未知变量有电位φs、离子势φ1、阳极氢质量分数w(H2)、阳极水质量分数wa(H2O)、阴极氧气质量分数w(O2)、阴极水质量分数wc(H2O)、阴极氮气质量分数w(N2)、阳极和阴极中的速率场矢量ua和uc、阳极和阴极中的压力pa和pc以及总发热功耗密度Qh。

模型通过耦合2个“反应流”接口和1个“二次电流分布”接口来实现求解。

在求解电化学电流方面，二次电流分布接口基于欧姆定律对电化学电流进行建模，求解气体扩散层（Gas Diffusion Layer，GDL）中的电位、多孔电极中的电位和离子势，以及电解质膜中的离子势。在多孔电极中，局部电流密度取决于离子势和电势，但也受反应物局部浓度的影响。

在阳极，氢氧化反应为：

随浓度变化的线性巴特勒-褔尔默（Butler-Volmer）表达式可用于阳极局部电流密度ia的计算：

式中，i0,a为阳极交换电流密度；c(H2)为局部氢浓度；cref(H2)为氢参考浓度；αa,a为阳极传递系数；αc,a为阴极传递系数；F为法拉第常数；R为气体常数；T为开氏温度；ηa为阳极活化极化电压。

在阴极，氧气与质子发生反应，形成水，反应式为：

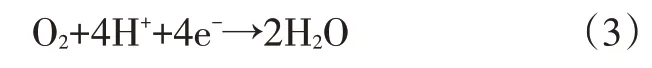
阴极氧还原反应的局部电流密度ic为：

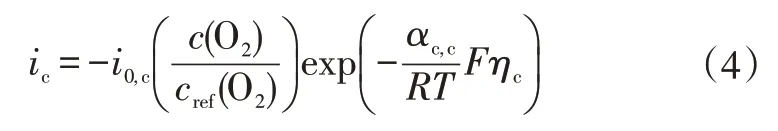
式中，i0,c为阴极交换电流密度；c(O2)为局部氧浓度；cref(O2)为氧参考浓度；αc,c为阴极传递系数；ηc为阴极活化极化电压。

式（4）是随浓度变化的简化Butler-Volmer 表达式，已忽略阳极项，也可以看作随浓度变化的塔菲尔（Tafel）方程。

设与阳极GDL接触的流道脊板位置电位为0，与阴极GDL 接触的流道脊板边界电位为电池的输出电压Vcell，所有其他外部边界都设置为绝缘。

求解质量传递方面，在2个不同的“浓物质传递”接口中使用Maxwell-Stefan 方程求解流道、GDL 和多孔电极中的w(H2)、wa(H2O)、w(O2)、wc(H2O)和w(N2)。对于阳极，求解氢气和水；对于阴极，求解氧气、水和氮气。

通过质量源和汇，将这2个接口与“二次电流分布”接口耦合。

在流道入口处指定了质量分数，在流道出口处使用流出条件。所有其他外部边界都使用零通量条件。

对于求解动量传递，借助“Brinkman 方程”接口；对于流道，通过纳维-斯托克斯（Navier-Stokes）方程对速度u和压力p进行建模；对于多孔GDL 和电极（Catalyst Layer，CL），通过Brinkman方程进行建模。

通过使用“反应流”多物理场节点，将“Brinkman 方程”接口与“浓物质传递”接口耦合，实现密度、速度、压力、净质量源、质量汇以及物质传递的耦合。

在流道入口边界，指定入口流速分布为层流流入，出口处指定压力边界条件。为了对多平行通道的情况进行建模，沿GDL 和多孔电极的长边应用对称边界条件。所有其他壁边界都应用了无滑移边界条件。

在此过程中可以同时求解出电池内部各组件的热功耗密度分布，包括欧姆极化、活化极化和浓差极化引起的热功耗。对热功耗密度Qh在电化学域内进行积分可得到电池的总发热功率Ph。

阴极生成水的速率Δm(H2O)可通过法拉第定律进行计算：

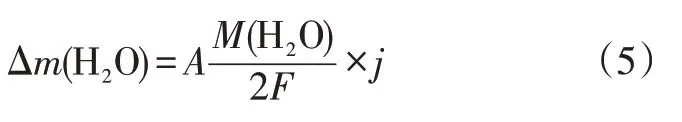
式中，A为MEA 的活性面积；M(H2O)为水的分子量；j为电流密度。

则水伴热值Q(H2O)为总发热功率Ph与产生水速率Δm(H2O)的比值：

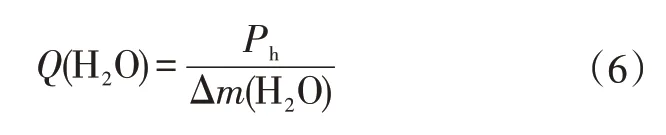
计算过程中用到的主要参数如表1 所示。本文计算了在相同空气流速Uin_ca、不同输出电压Vcell（0.05～0.80 V）下以及在相同输出电压Vcell（0.2 V）和不同空气流速Uin_ca下（对应不同计量比Ca.S.R.）的电池发热功率分布情况以及水伴热值。

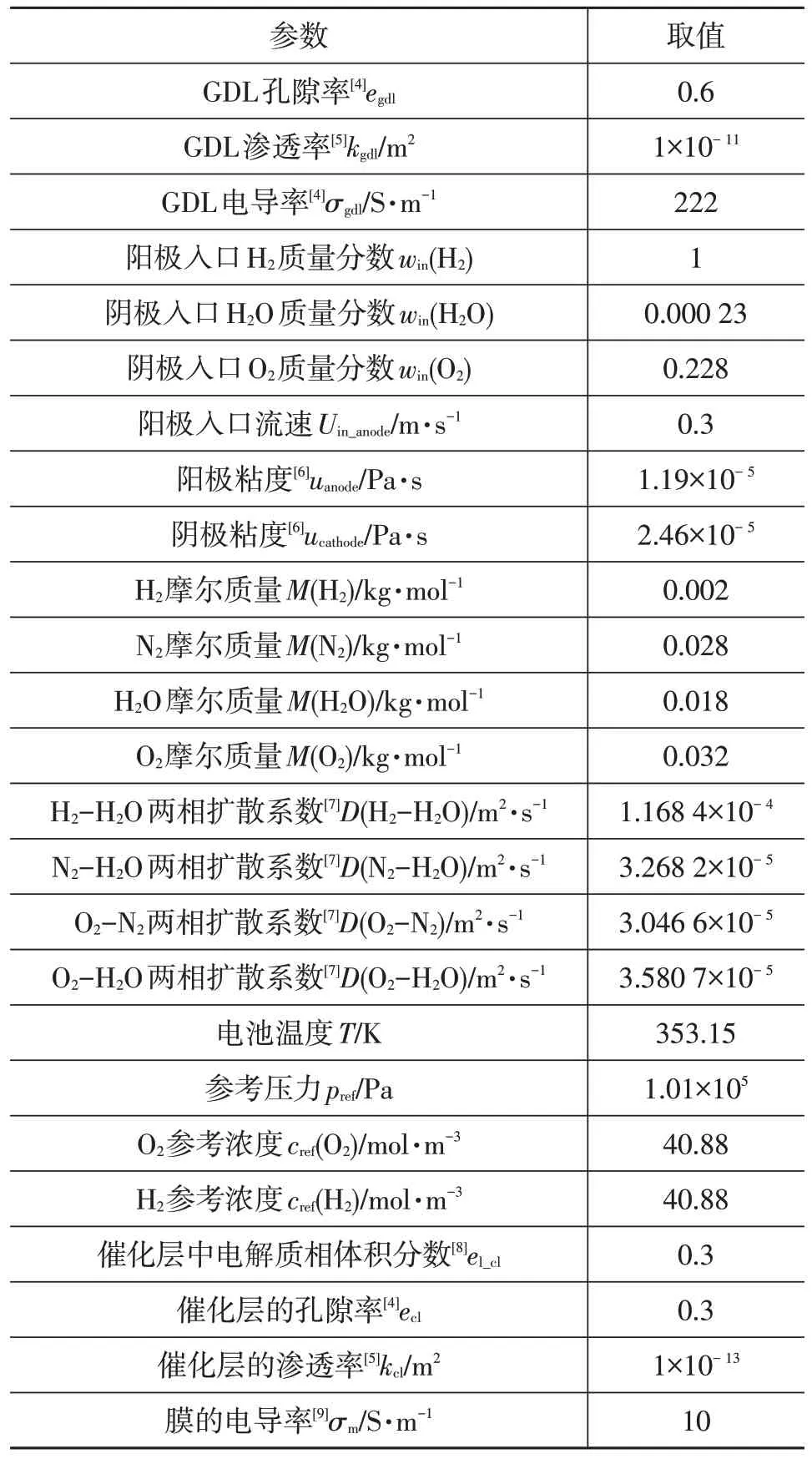
表1 主要参数取值

2.2 前提假设

为简化模型求解，本文进行以下假设：

a.气体和混合物为理想气体，且符合菲克定律；

b.电池温度为恒定值，且忽略极化热等参数受温度变化的影响；

c.电池内部气体流动为层流；

d.膜和催化层是各向同性和均匀的；

e.由于本文是基于低温启动特性评估进行的仿真，而非对冷启动过程进行仿真，因此，假设在其他条件不变的条件下，水伴热值Q(H2O)越大，冷启动成功率越高；

f.因为针对冷启动过程的瞬态仿真尚不成熟且精度较低，这里采用稳态计算，不考虑膜离子电导率受水含量变化的影响，且不考虑电池中各物理量的瞬态变化；

g.不考虑氢气和空气在膜两侧的渗透情况。

2.3 几何尺寸

图1给出了单流道PEMFC模型的3D几何结构。该模型包括阳极流道、阳极GDL、阳极催化层（Anode Catalyte Layer，ACL）、膜、阴极催化层（Cathode Catalyst Layer，CCL）、阴极GDL 和阴极流道，共7 个域。几何参数参考实际电池尺寸取值，如表2所示。

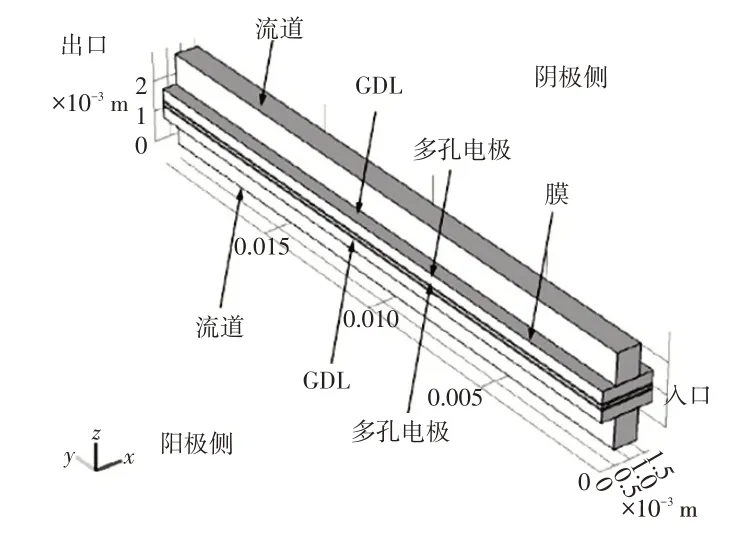
图1 模型的几何结构

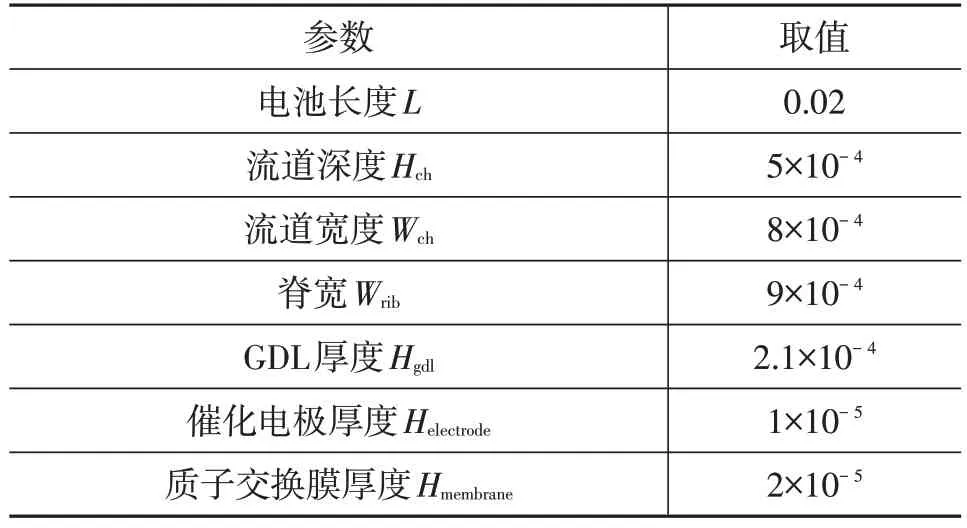
表2 几何参数 m

3 计算结果与数据分析

3.1 热源种类及发热功率占比

燃料电池内部的总热源Ph主要分为阴极极化热Pca、阳极极化热Pan和欧姆热Pohm3 个部分，欧姆热主要考虑两侧GDL层和质子交换膜中电子和离子传导产生的热。在相同输出电压和不同阴极计量比下，3种热源发热功率的计算结果如表3所示。

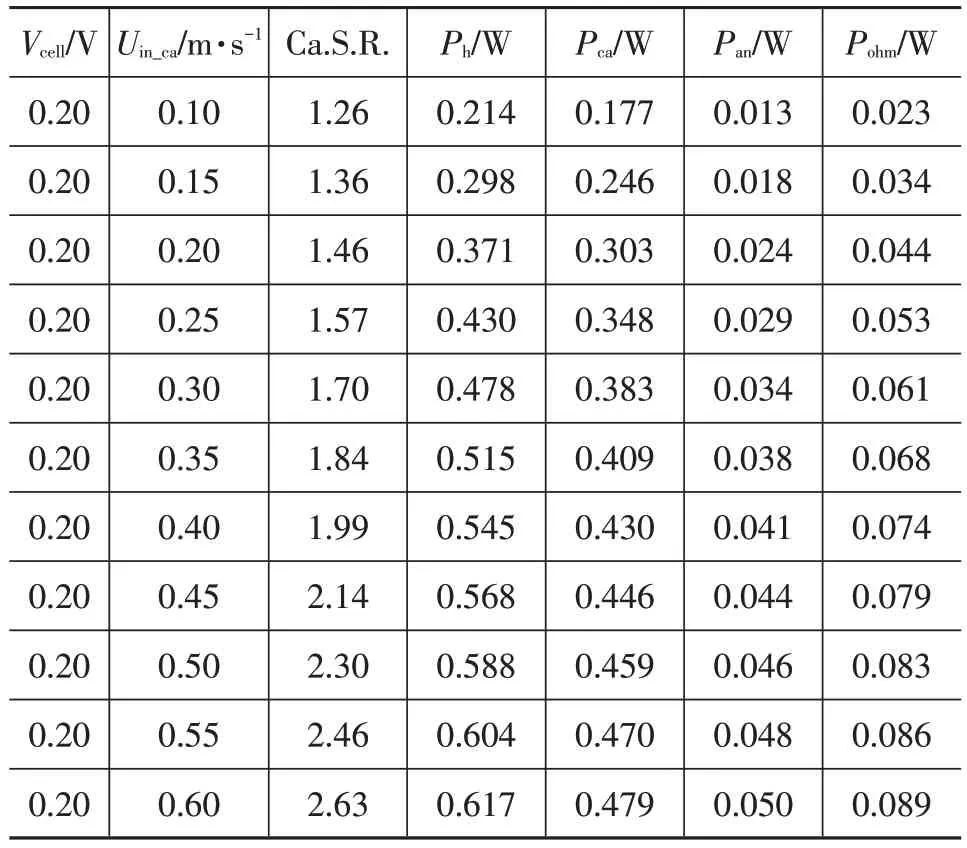
表3 相同输出电压和不同阴极计量比下热源与发热功率

从表3 中可以看出，在阴极计量比为1.99 时（接近实际值），0.2 V 电位下该电池的整体发热功率约为0.545 W，其中阴极催化层发热功率占比79.6%，阳极催化层发热功率占比7.4%，而分布在质子交换膜和GDL层中的欧姆发热功率占比13.0%。由此可见，产热主要集中在阴极催化层区域，这与阴极氧还原反应本身反应速率较低是一致的。同时，也可以看出这种发热情况有利于低温启动，因为阴极催化层也是水首先出现的位置。

图2 给出了分热源发热功率随阴极计量比的变化情况，可以看出，随着阴极计量比的提升，总发热功率不断变大，这意味着电堆将会升温更快，启动速度也会更快。阴极催化层的发热功率也随之增加，但增加速率趋缓。

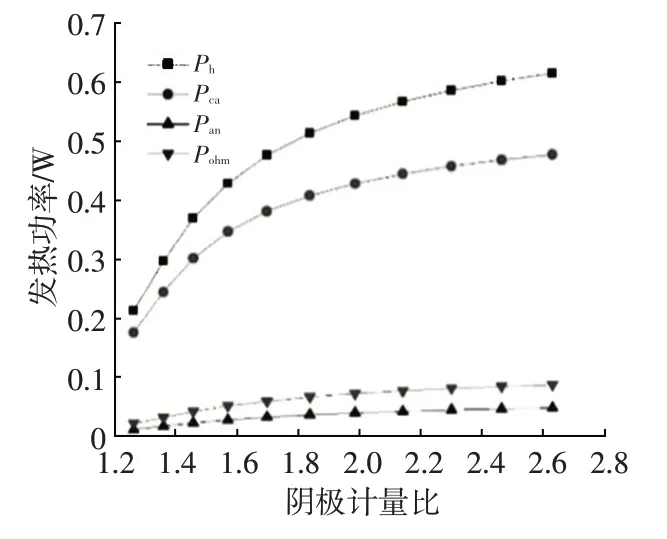
图2 分热源发热功率随阴极计量比变化情况

3.2 阴极催化层发热功率分布

在燃料电池发热功率中，阴极催化层占比最高，因此重点考虑阴极催化层的热量分布情况。图3 给出了阴极催化层发热功率密度分布随阴极计量比的变化情况。可以看出，计量比越低，发热功率分布越不均匀，热量主要集中在阴极入口附近区域，在计量比为1.26时，发热功率密度最高值与最低值相差达到6 个数量级。而最低发热功率密度通常出现在阴极出口附近和两侧脊下区域。

当计量比提升至2.63 时，发热不均的情况明显得到改善，发热功率密度最高值和最低值相差约3个数量级，此时入口和出口之间的差别已经不大，低发热功率密度主要出现在脊下区域。可见，在冷启动过程中，脊下区域发热功率密度普遍较低，该部分也最容易发生结冰。

在冷启动过程中，通常根据工况控制单体输出电压值以实现成功启动。本文对相同流量下不同输出电压时阴极催化层的发热功率密度分布进行了计算，结果如图4所示。可以看出，当电压低至0.1 V时，电池内部的发热情况极端不均匀，发热功率密度最高值与最低值相差达到9 个数量级，这种情况对燃料电池各零部件，尤其是双极板和GDL 层的导热能力要求很高。从图4 中还可以看出，当输出电压较高时，脊下位置的发热功率明显得到改善。这种现象也可以为冷启动控制策略的制定提供一定参考。

图3 不同阴极计量比下的阴极催化层发热功率密度分布

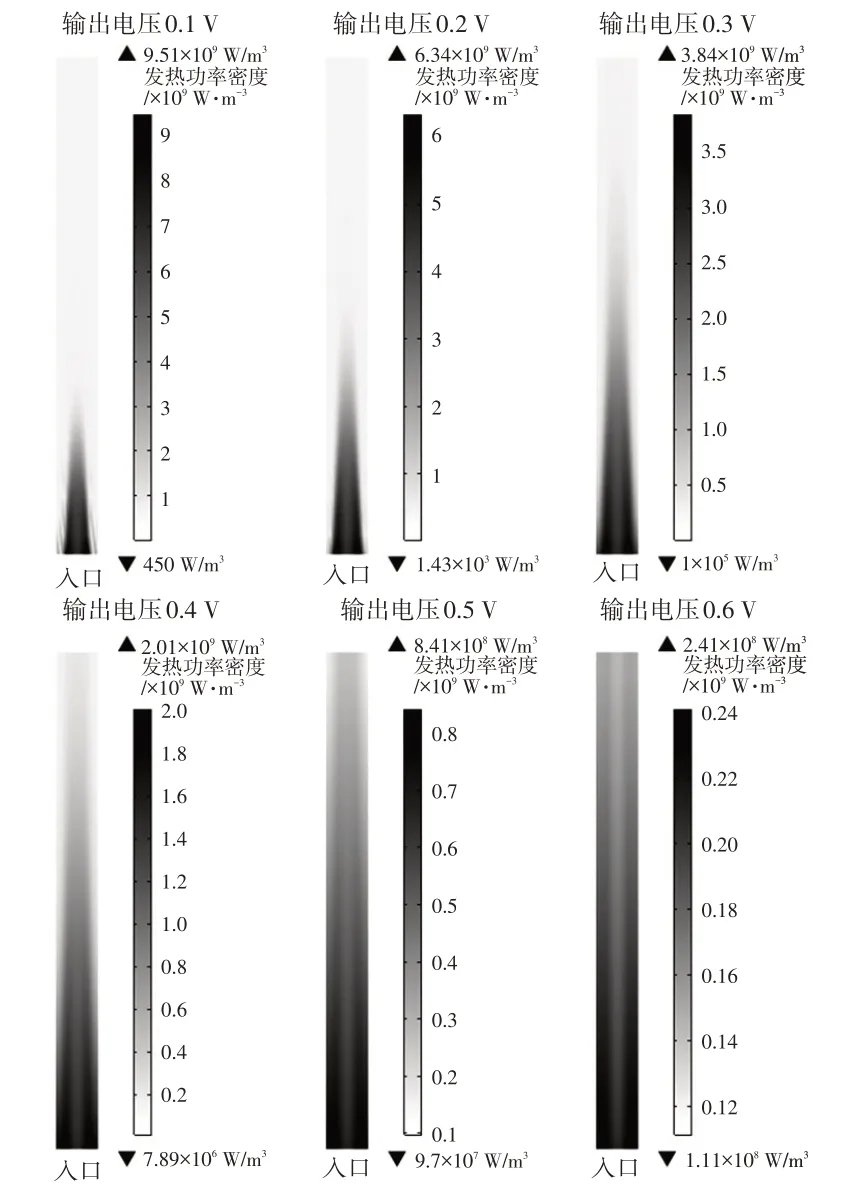
图4 相同流量不同输出电压下阴极催化层的发热功率密度分布

3.3 水伴热值

表4给出了在相同流量、不同输出电压下电池内部工作状态的计算结果。包括总发热功率、产水速率、水伴热值等指标。

表4 相同流量不同输出电压下电池内部工作状态计算结果

从表4 中可以看出，每生成1 g 水，当输出电压为0.1 V 时，燃料电池内部能够产生的热量是输出电压为0.6 V时的约2倍。

根据表4中数据，对水伴热值随输出电压的变化情况进行作图，如图5 所示。可以看出，随着输出电压的升高，生成单位质量水产生的热量呈线性减少，这说明可以通过控制输出电压的方式在保持生成水量不变的条件下提高产生的热量，这也是冷启动过程中面临的核心问题。输出电压越低，水伴热值越高，这是因为燃料电池发电效率降低导致了更多的化学能转化为热能。

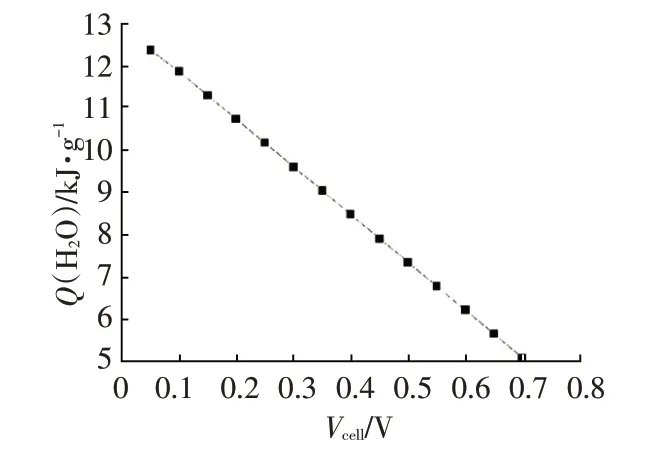
图5 水伴热值随输出电压的变化曲线

为考察计量比对水伴热值的影响情况，对其进行计算，结果如表5 所示。根据表5 中数据，对水伴热值和水生成速率随阴极计量比的变化情况进行作图，如图6 所示。可以看出，在特定输出电压下，计量比的变化基本不会影响水伴热值的变化。然而，生成水的速率Δm(H2O)随着阴极计量比的增加而增加，这意味着可以通过控制阴极计量比来控制电池在冷启动过程中的产水速率。

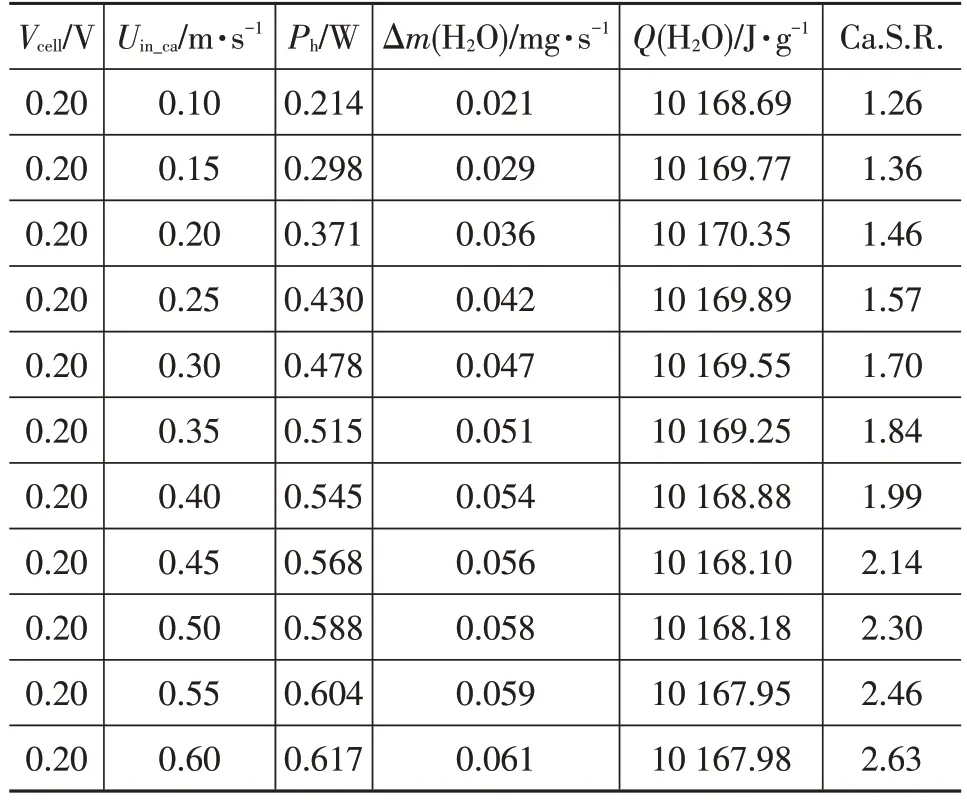
表5 相同输出电压不同阴极计量比下电池内部工作状态计算结果

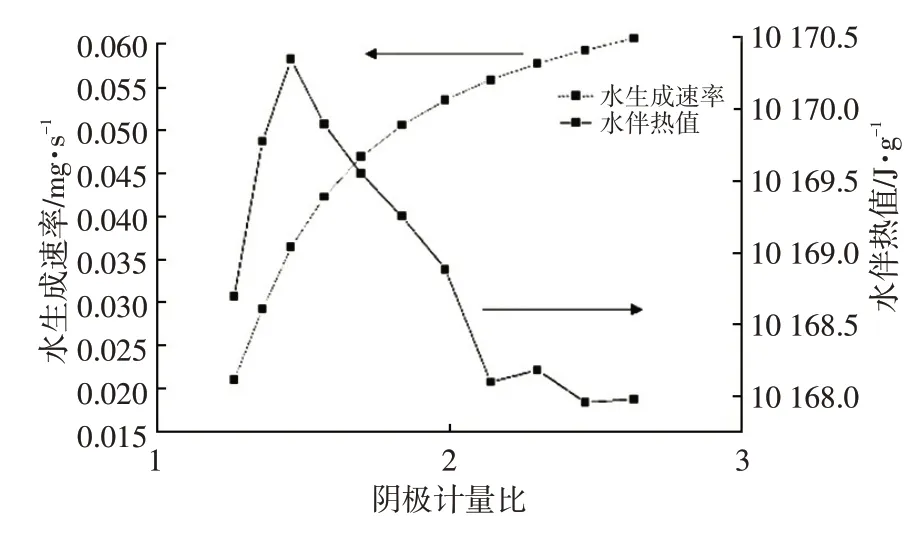
图6 水伴热值和水生成速率随阴极计量比的变化曲线

4 结束语

本文采用Comsol 软件建立了质子交换膜燃料电池3D 仿真模型，对不同输出电压和计量比下电池内部的热源发热功率占比、阴极催化层的发热功率密度分布情况进行了计算，并引入水伴热值概念，深入探讨了如何在控制产水量的同时，最大限度提升燃料电池的发热功率以提高冷启动的成功几率。

计算结果表明：燃料电池内部产热主要集中在阴极催化层区域，且该区域产热的占比随阴极计量比的降低而升高，同时，计量比越低催化层内发热功率分布越不均匀；可通过拉低输出电压来提升水伴热值，当电压从0.6 V 降低至0.1 V 时，相同产水速率下，总发热功率可提升约1 倍；在特定输出电压下，计量比的变化基本不会影响水伴热值的变化，但生成水的速率随着阴极计量比的增加而增加。

综上，在冷启动控制策略制定时，可通过适时控制阴极计量比和输出电压达到提高水伴热值、控制热源占比、发热分布和产水速率的效果；在双极板和MEA等材料选型时，考虑电化学性能和热质量的同时也要重视对热传导系数和耐热性的考虑，以应对冷启动过程中发热极为不均的情形。