谈几何画板与初中数学教学整合的实践应用

邹蕴

摘要：初中数学新课程标准中明确指出：要善于利用信息技术手段，创新教学模式和学习环境，在改变教法和学法的过程中，促进学生对知识的理解和消化，促使知识、能力、品质得到共同培养。而几何画板在初中教学中的应用，既可以化解抽象概念，又可以解析重点，提高问题解决能力，认识动点应用变化等，因此，本文就几何画板在初中数学教学整合中的应用实践进行了探究分析。

关键词：几何画板;初中数学;整合

1几何画板概述

GSP软件之所以受到广大教师的欢迎，是因为它可以通过测试几何形状猜想、关系猜想和变换来帮助教师进行教学。当用户操作对象时，屏幕上显示的测量值也会发生变化，用户可以拖动和改变物体的位置，而不需要重新绘制，从而给用户特别是学生更多的时间来思考几何，不需要浪费时间重建图表。这可以帮助学生探索一些难度更大的事情，而不再仅仅依赖于教科书、纸张和铅笔，这些活动明显提高了学生的认知能力。Teoh&Fong（2005）指出，动态可视化教学法有助于学生更好地理解所教授的数学概念。

2几何画板在初中数学教学整合中的应用路径

2.1.几何画板整合抽象概念，夯实基础知识

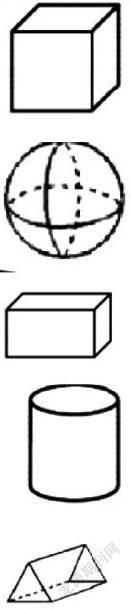
概念是学生学好数学，认识数学本质的前提。在以往数学概念教学中，对于复杂、抽象的概念都是通过复述讲解，或者死记硬背展开的，不仅枯燥乏味，还会降低学习兴趣。故此，为夯实基础知识，提高数学学习效果，可以利用几何画板与概念教学进行整合，通过形态化的视频展示，促使学生理解基本概念，用图形引导其认识概念语言本质。从而打破死记硬背的学习方法，提高概念教学质量。例如，在教学《立体图形与平面图形》数学内容时，重点是建立立体图形与平面图形的概念与区别，可以促使其能够从实物外形中抽象出几何图形。故此，在教学的时候，可以先利用信息技术手段为学生播放城市建筑、乡村住宅、立交桥、交通标志、剪纸艺术、城市雕塑、动物形态等，在直观视频播放的过程中，让学生认识图形世界的多姿多彩，感知数学在生活中的应用价值。然后为学生展示生活中最熟悉的纸箱，如：

利用几何画板画出以下图形，如：

在利用几何画板直观展示的过程中，让学生思考，从整体看，它的形状是什么_____，从不同侧面看，是____和____，看棱可以得到____，看顶点可以得到___

在问题思考和观看的过程中，为学生引出几何图形的概念，然后就几何图形为载体，利用几何画板绘制以下图形，如：

让学生思考他们有什么共同的特点？其平面图形是什么？有什么特点？结合生活实际举出相应的实例，“茶叶罐、金字塔、帐篷”在几何画板直观使用的过程中，促使其充分认识立体图形和平面图形的概念，使其会区分立体图形和平面图形，在整合几何画板和数学概念基础知识的基础上，为学生学好数学奠定坚实的基础。

2.2几何画板解析重点内容，促进理解掌握

重难点教学解析向来都是教学的重要内容，也是中考的必考知识点。在初中数学课堂教学中，要想让学生掌握并理解重点内容，思维启发，数学思想培养是关键。故此，为实现几何画板与数学教学整合，可以在解析重点内容时进行教学辅助，在高效引导、知识和转化的过程中，实现难点化解，加强记忆和理解，激发数学学习自信心。例如，在教学《全等三角形》数学内容时，重点是让学生认识全等三角形的特点，发现全等三角形的性质。因此，在教学的时候，可以先利用信息技术手段，在课件中播放能够完全重合的两个平面图形，如两面相同的树叶、相同的剪贴画等，在直观视频播放的过程中，引导其自主探究全等图形的概念，總结其特点，认识全等性图形的特征为：形状、大小完全相同的道理。然后利用几何画板，画一个三角形，展现图形平移、翻折、旋转前后的图形位置改变，形状、大小不变的场景，让学生说一说全等三角形具有什么特点，全等三角形的对应顶点、对应边、对应角如何？引导学生根据几何画板的直观演示，寻找对应边、对应角的规律，如：

在全等三角形中，有公共边的，则公共边为对应边

在全等三角形中，有公共角的，则公共角为对应角

在全等三角形中，有对顶角的，则对顶角为对应角

通过认识全等三角形的特征和性质，使其对全等三角形有一个清楚地了解，为学生接下来掌握全等三角形判定性质，奠定坚实的基础。这样既可以促进对重点知识的理解和消化，又可以避免死记硬背，在灵活探索的过程中，提高学习能力，培养数学抽象、数学建模等综合素养。

2.3几何画板搭建问题模型，认识问题本质

数学证明推导问题是教学的重点内容，也是培养学生数学建模和直观想象素养的关键。但是，在以往教学中，都是以口述或者粉笔画进行的引导，导致学生对这一解题形成过程，以及问题推导缺乏有效理解，从而致使解题失误。而几何画板的有效应用，可以充分以问题为原型，搭建数学模型，不仅可以使其看清问题本质，还可以促使其对问题探究过程有一个充分的认识。例如，在教学解析有关勾股定理数学内容的时候，为让学生能够更好地应用a2+b2=c2定理公式进行问题解决，在解析勾股定理问题的时候，可以利用几何画板构建问题模型，在数形对比分析的过程中，促使问题解析直观化，从而提高问题解决能力，如：

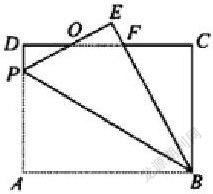
在矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD，求AP的长。

对于这一问题解析，倘若直接求解推理，很容易出现没有解题思路的现象，故此，在解析的时候，教师可以利用几何画板依据题意绘制直观图形，如：

根据直观图形的设计展示，让学生结合题意分析，求AP的长可以将其放入△EBP中，围绕△EBP为入口点，引导其设AP=EP=x，EB=AB=8，∠E=∠A=90°，因为∠D=∠E=90°，OE=OD，∠DOP=∠EOF，所以△DOP≌△EOF，DP=AD-AP=6-x，EF=Dp=6-x，OP=OE，因为OE=OD，所以DF=PE=x，所以CF=CD-DF=8-x，因为EF=6-x，BE=8，所以BF=BE-EF=8-（6-x）=x+2，在RT△BCF中，CF2+BC2=BF2，从而求解AP的值。通过直观图形的展示，在数形结合的过程中，提高学生对问题的认识，使其在解析的时候有一个清楚的解题思路，在几何画板与应用问题探索整合的过程中，培养学生数形思想，提高问题解决能力，让学生乐学数学，培养直观想象和数学建模素养。

3结语

综上，在初中数教学中运用几何画板，可以提升教学效果，同时也是对传统教学模式的一次冲击，让数学课堂变得更加生动。学生在此过程中也表现得更加积极，有强烈的求知欲，提升课堂效率。

参考文献

[1]石小菲.谈几何画板与初中数学教学整合的实践应用[J].科学咨询（科技·管理），2020（10）：257.

[2]魏国平.谈几何画板与初中数学教学的融合策略[J].新课程，2020（37）：121.

沈阳市第八十二中学 辽宁省沈阳市 110000