基于非参数检验和ARIMA模型的芜湖市空气质量指数研究

余婉风 吕科 刘洋 朱伟杰

摘要：在近几年全国空气质量总体有所好转的大环境下，本文通过分析芜湖市空气质量指数数据，探究芜湖市空气质量现状，并构建AQI短期预测模型，为芜湖市政府控制环境污染和有效地治理提供科学的依据。2013年12月1日—2020年10月31日近8年芜湖市空气质量指数（AQI）数据作为研究对象，R语言为实现工具。首先，分析AQI数据曲线图，采用非参数检验Kruskal-Wallis检验比较这8年AQI数据是否具有显著性差异;其次，根据对AQI时间序列平稳性分析结果，选择合理的时间序列模型—ARIMA模型，估计模型参数，建立拟合模型，并评价模型有效性;最后，利用模型预测未来几个月AQI。

关键词：AQI;非参数检验;时间序列分析;ARIMA预测模型; R语言

中图分类号：TP391      文献标识码：A

文章编号：1009-3044（2021）11-0239-03

Study on Air Quality Index（AQI） of  Wuhu City Based on Nonparametric Test and ARIMA Model

YU Wan-feng， LV Ke， LIU Yang， ZHU Wei-jie

（College of Big Data and Artificial Intelligence， Anhui Institute of Information Technology， Wuhu 241003，China）

Abstract： In recent years， air conditions nationwide has been improving， through analyzing the air quality index data of Wuhu city， to explore the current situation of air conditions of Wuhu City， and model for AQI prediction ， which provides scientific basis for Wuhu city government to control environmental pollution effectively. From December 1， 2013 to October 31， 2020， air quality Index （AQI） data of Wuhu city in recent 8 years were taken as the research object， and R language was used as the implementation tool. Firstly， the AQI data graph was analyzed， and the kruskal-Wallis test was used to compare the significant differences of the AQI data over the past 8 years. Secondly， according to the stationary analysis of AQI time series， an reasonable time series model -- ARIMA model is selected， to estimate fitting model parameters and evaluate the effectiveness of the model. Finally， the ARIMA model is used to predict AQI in the coming months.

Key words： AQI; nonparametric tests; Time-Series analysis; ARIMA prediction model; R softwre

随着城市工业的成长壮大，空气污染严重，空气质量恶化，不仅影响到人们的正常生活，而且威胁着人们的身心健康[1]。环保作为国家战略性重点产业，全国各级政府对本省市的环保工作高度重视，纷纷积极推动节能减排和环境治理工作，截至目前，全国几乎所有的省市，均已出台生态保护相关政策、资金支持或项目管理方案，为我国全面推进环保事业提供有力的支持[2-3]。芜湖市政府以科学发展观为指导，紧紧围绕国家环保总局提出的七个方面整改要求，开展集中整治行动，推进环保执法，推进节能减排，推进全市经济发展模式的转变[4]。

同时，随着R语言中各类工具包（package）的不断涌现，数理统计分析工具和可视化方案的R程序包得以开发应用开来。本研究数据来自2013年-2020年日报AQI数据，非参数检验Kruskal-Wallis检验可以对多组独立样本的多重比较，安装、引用R语言pgirmess程序包，调用kruskalmc函数实现Kruskal-Wallis检验[5];利用R语言软件包tseries进行时间序列分析;调用软件包forecast的auto.arima（）函数进行系统定阶，拟合最优ARIMA模型。本文中，运用非参数检验对比近几年芜湖市空气质量指数有无明显改善;应用时间序列分析建立预测模型，对模型进行参数估计，诊断和评价，确定最优模型，并检验模型有效性[6]，最后运用模型进行预测。

1 非参数检验—Kruskal-Wallis检验

1.1抽样数据

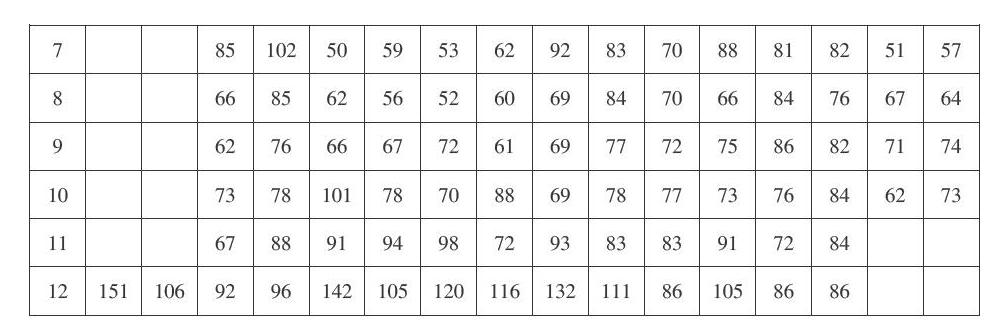
研究对象是芜湖市2013年12月到2020年7月的空气质量指数（AQI），取每个月AQI平均值。

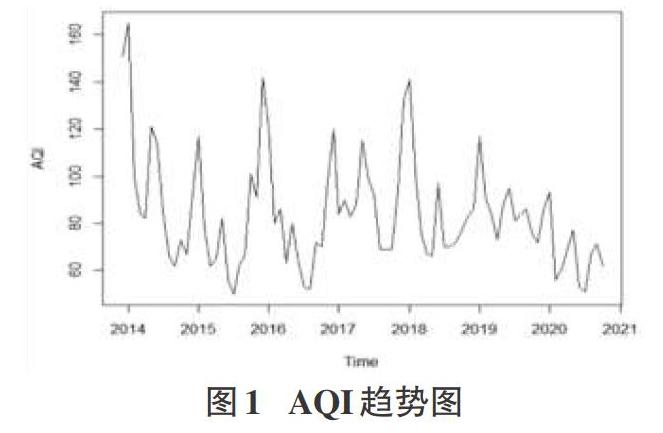
为了更直观地分析2013年到2020年AQI的变化趋势，描绘数据趋势图。如图1所示，2013年12月到2020年10月芜湖市空气质量指数（AQI）有逐年降低趋势，但不明显，且可能呈周期性变化。僅从图1无法确定AQI是否有明显的逐年降低趋势，且考虑到AQI分布未知，样本量少，采用非参数检验进行8组独立样本的多重比较，判断不同年份的AQI数据是否具有统计学差异。

1.2 R语言实现Kruskal-Wallis秩和检验

利用抽样技术，从2013年12月到2020年10月中抽取每个月1号的数据，即83个样本数据，不同年份作为组别，共有8个独立组别。安装并加载程序包pgirmess，调用Kruskal-Wallis秩和检验函数计算结果p-value=0.02139，显著性水平α=0.05，p-value小于显著性水平，说明拒绝原假设（原假设是8组样本数据无显著性差异），即这8年的AQI数据有显著性差异。结合图1分析，可以认为近几年芜湖市的空气质量指数有明显的降低趋势，空气质量明显好转，环境治理效果显著。为了给芜湖市政府控制空气污染和有效地治理提供科学的依据，分析数据特征，建立有效的AQI预测模型。

2 AQI时间序列预测模型

从2013年1月到2020年10月芜湖市空气质量指数（AQI）总趋势虽无明显降低，但AQI不是杂乱无章的，如图2所示，分解了数据的变化趋势、季节性和不确定性因素，分析图中“seasonal”曲线， AQI有明显的季节性、周期性趋势。基于AQI的数据特征，采用时间序列分析建立AQI短期预测模型，在预测模型有效的前提下利用模型预测2020年未来几个月的空气质量指数，并绘制拟合图形。

2.1 平稳性分析

（1）平稳性分析

常见的时间序列模型包括ARAM和ARIMA模型等，根据时间序列的平稳性来选择合适的预测模型，常见的时间序列平稳性检验方法有PP检验法和ADF检验法。

R软件安装加载tseries包，进行PP检验和ADF检验。PP检验结果中出现警告信息，ADF检验p值=0.04803< 0.05，默认显著性水平[α=0.05]，拒绝原假设（原假设认为时间序列是非平稳的），可以认为AQI数据是平稳的时间序列。

（2）白噪声检验

对于平稳的时间序列需要进行白噪声检验，因为白噪声是纯随机序列，对纯随机序列建模毫无意义。对AQI时间序列白噪声检验结果p值=4.6637e-07小于显著性水平0.05，拒绝原假设，可以认为AQI数据为非白噪声时间序列，对该平稳时间序列建模有意义。

考虑到AQI呈季节性、周期性变化，选择目前最常用的拟合平稳序列的模型ARAM（p， q）模型（自回归移动平均模型）作为AQI时间序列预测模型。ARMA模型（自回归移动平均模型）又可以细分为AR（p）模型、MA（q）模型和ARMA（p， q）模型三大类，确定AQI预测模型属于哪一类这都取决于阶数p和q的值，其一般准则如表1所示。

2.2 确定ARAM（p， q）模型阶数p和q

对于ARAM（p， q）模型，一般通过分析ACF自相关图和PACF偏相关图来估计两个未知参数p和q。在R软件中，拟合线性回归模型，再调用acf（）和pacf（）两个函数绘制ACF自相关图和PACF偏相关图。

图3中，自相关系数拖尾，且从1开始控制在置信区间之内，p= 1;图4中，偏相关系数拖尾，且从2开始控制在置信区间之内，q= 2。根据表1确定ARAM模型准则，初步推测AQI预测最优模型为ARMA（1， 2）。

2.3 系统自动定阶

为了验证通过时间序列稳定性、ACF自相关图和PACF偏相关图分析确定的ARAM（1， 2）模型是否比较合理，利用R语言软件包forecast的ARIMA模型函数，默认预测模型为ARIMA（p， d， q）模型（差分整合移动平均自回归模型）进行系统自动定阶，与通过平稳时间序列ACF自相关图和PACF偏相关图分析确定的ARAM（1， 2）模型进行比较，找到最优模型。安装、加载forecast包，时间序列ARIMA建模，结果如表2，ARIMA（1，0，0）（2，0，0）12 是拟合AQI时间序列的最佳模型，其中参数p= 1，d= 0，q= 2。参数d表示差分阶数，当d为0时，ARIMA模型就等同于ARMA模型，即ARIMA（1， 0， 2）模型与ARMA（1， 2）模型是等价的。由此，通过分析自相关系数图和偏相关系数图确定的最优模型与R语言进行系统自动定阶结果一致。

在确定了最优模型ARIMA（1，0，2）模型之后，并采用极大似然估计思想进行参数估计，如表2，ARIMA（1，0，2）拟合模型：

[yt=0.6101yt-1+0.3725εt-1+0.2043εt-2+84.4825]

接下来，对ARIMA（1，0，2）模型的3个系数和1个截距进行假设检验，用极大似然估计思想估计的系数的绝对值除以其标准差（s.e.）得到的商与t检验5%的临界值1.96比较，商的绝对值大于1.96，拒绝原假设（原假设为参数影响不显著），否则认为参数影响显著。t（ar1）= 6.532> 1.96， t（sar1）= 3.242> 1.96，t（sar2）= 1.625< 1.96， t（mean）= 9.621> 1.96，所以参数ar1、sar1和截距对该时间序列模型都具有显著影响。

2.4 预测模型有效性检验

常用的检验ARIMA模型有效性的方法是纯随机性检验方法Box-Ljung检验，R语言提供了Box-Ljung检验的tsdiag（）函数。调用tsdiag（）函数，检验结果如图5所示。

第二行的ACF检验说明残差没有明显的自相关性;第三行的Box-Ljung检验显示所有的p值都大于显著性水平0.01，残差序列不能拒绝纯随机的原假设，说明残差为白噪声，所以此预测模型是有效模型。利用ARIMA模型预测过去8年的AQI数据，将预测值与真实值对比，如表3所示，该预测模型在误差允许的范围内能反映AQI数据的变化趋势和规律，有参考价值。

3 ARIMA模型预测未来空气质量指数

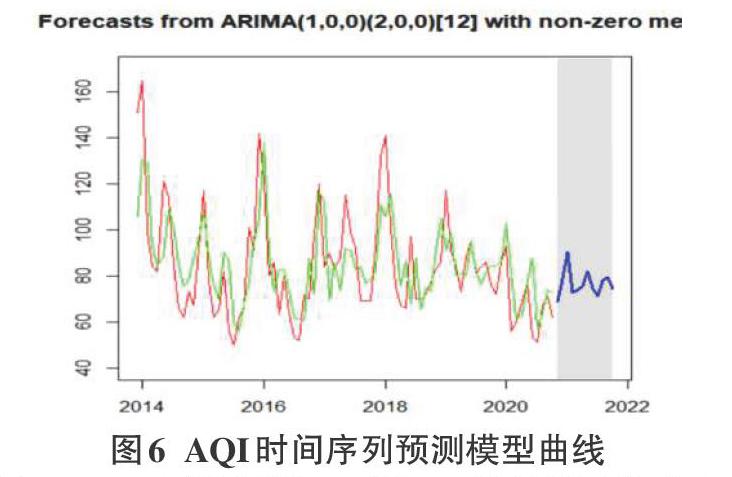
在检验ARIMA（1， 0， 2） 预测模型是有效的前提下，利用预测2020年未来几个月的空气质量。调用forecast（）函数绘制预测模型曲线，如图6所示，两条曲线分别表示AQI时间序列和ARIMA（1， 0， 2）模型，右邊粗线表示预测模型预测的未来几个月AQI序列。

调用forecast（）函数预测11月和12月每月平均的空气质量指数，有：

[predict（AQI—11）=68.67];

[predict（AQI—12）=78.73]。

4 总结

时间序列模型的缺点是精确度不够高，为了提高精确度，可以在模型中增加与空气质量相关的变量如PM2.5、CO和N02含量等相关变量。考虑到目前芜湖市政府正在逐渐加大环保力度，从长期来看，由于外部因素干预加强，导致模型的预测能力下降，所以此模型较适合短期内预测。

参考文献：

[1] 史美义.浅析当前我国城市环境污染的现状及原因[J].科技信息，2012（18）：79.

[2] 国务院.国务院关于落实科学发展观加强环境保护的决定[J].中国环境监测，2006，22（1）：1-6.

[3] 安徽省人民政府.安徽省人民政府贯彻国务院关于落实科学发展观加强环境保护决定的实施意见[J].安徽省人民政府公报，2006（21）：21-26.

[4] 付伟，司红君，卢尧，等.芜湖市空气质量特征及其受气象要素的影响分析[C]//第35届中国气象学会年会论文集.合肥，2018：128-129.

[5] 金英良，赵华硕，孙桂香，等.基于R软件的多组独立样本秩和检验的多重比较[J].预防医学论坛，2016，22（11）：805-806，809.

[6] 牟敬锋，赵星，樊静洁，等.基于ARIMA模型的深圳市空气质量指数时间序列预测研究[J].环境卫生学杂志，2017，7（2）：102-107，117.

【通联编辑：唐一东】