多区间速度约束下的时序数据清洗方法∗
高 菲,宋韶旭,2,3,王建民,2,3
1(清华大学 软件学院,北京 100084)
2(大数据系统软件国家工程实验室,北京 100084)
3(北京信息科学与技术国家研究中心(清华大学),北京 100084)
1 引 言
随着信息技术的普及和发展,各行各业通过相应的信息系统积累了大量的数据,进一步为大数据以及人工智能技术提供了基础数据支持.针对大数据以及人工智能技术,为了能更好地发挥其优势、提升其效率、推广其应用,数据管理与分析技术作为其基础性支撑不可或缺.众所周知:由于传感器、终端记录器等设备在数据采集、数据传输、数据记录等过程中会受到主观和客观因素的影响,受制于物理和技术上的约束,最终所得到的数据会存在一定的数据质量问题.当数据质量存在问题时,所采集到的数据并不能准确地反映出真实世界的表征,进而无法形成其对人工智能技术的优化促进作用.解决数据中的异常问题、提升数据质量,可以推动数据管理分析对人工智能在数据环节的优化,促进人工智能领域的发展.
1.1 问题背景
目前,数据质量问题所产生的成本和风险不容小觑,有效地识别和修复数据中存在的异常,已经成为数据管理领域中的重要课题.随着技术的进步,数据的存储和传输成本大幅度下降;同时,由于大数据及人工智能技术的发展,数据惊人的潜能不断被挖掘,人类社会,尤其是工业领域,更趋向于尽可能地将能够产生的数据记录存储下来.通常情况下,这些数据大多是时间序列数据,也就是包括时间戳在内的一系列数据点.
时间序列数据普遍存在于人们的日常生活以及工业领域中,例如行车路线、温度变化、股票走势等.由于大部分时间序列数据中数据点会随着时间的变化而产生一定的变化规律,Zhang 等人提出了基于速度约束的SCREEN 方法[1]对时间序列数据进行异常修复.该方法采用速度约束范围[smin,smax]([最小速度,最大速度])来对数据的变化速度进行约束,进一步将超出速度约束范围的数据点视为异常点并进行修复.但该方法仅适用于单一速度约束区间,即速度变化范围在一个最大值和一个最小值之间.而实际数据中,数据的速度变化将很可能存在多个速度约束区间.举例来说,速度变化很可能在或区间中若仅将变化速度约束为,那么所约束的很多正常点将被视作异常点进行修复.同理,若仅将变化速度约束为,那么所约束的正常点同样会被视作异常点从而产生过度清洗.此外,若将变化速度约束为,那么之间的异常点则会被视作为正常点而不作任何修复.无论是哪种情况,都将大大降低数据的修复质量.
例1:公司对车辆油耗数据进行监督,以分析油耗情况,进一步合理行车,减少成本.在此时间序列数据中,包括耗油和加油两种行为,如图1 所示.由于车辆在行驶过程中是一个耗油状态,所以油箱中的油位整体呈一个下降趋势.但车辆在行驶过程中不可避免地会存在颠簸,油箱中的油位测量也会存在一定小范围的振荡,所以在耗油过程中,油位持动态下降趋势,具体速度约束为[−1,1],即每单位时间内油位的变化在减少1cm 到增加1cm 的范围内浮动(根据真实数据情况,该示例中将单位时间设置为5s).而在加油过程中,油位数据为骤然增长态势,具体速度约束为[20,70],即在加油过程中,每单位时间内油位增加20cm~70cm.若给定时间窗口内两数据点间的数据变化速度在上述[−1,1]及[20,70]区间范围外,则该数据变化速度异常,这两个数据点必然存在异常数据.如图1所示,蓝色数据为异常数据点.
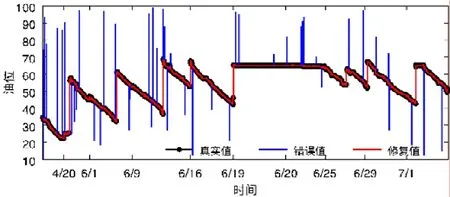
Fig.1 Example of fuel consumption data图1 油耗数据示例
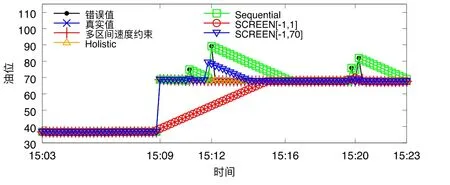
为了更清晰地表明多区间速度约束和单区间速度约束的区别,本文从上述油耗数据集34 220 个数据点中选取100 个数据点进行修复.在此数据中,若贸然将速度约束定为[−1,1],那么加油行为则被视为异常数据被修复,如图2 所示,因为15:09 时刻的加油行为,后续较多正常值被误判为异常值进行过度修复;同理,若速度约束为[20,70],则大量耗油行为将被视为异常数据从而导致过度修复.而若采用速度约束[−1,70],则大部分数据都被视作为正常点,而速度约束在(1,20)内的异常点将无法被有效识别并修复,如图2 所示,由于15:12 时刻一个异常点的的存在,导致后续多个正确值被误修.
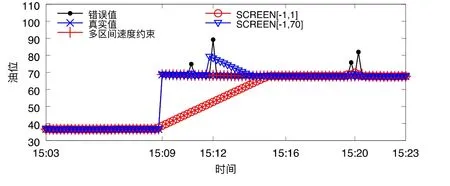
Fig.2 Repairing with SCREEN and multi-speeds constraints图2 基于SCRREN 方法及多区间速度约束方法下的修复效果
基于此,本文主要针对时间序列数据的数据质量问题进行研究,进一步通过多区间速度约束对时序数据中的异常进行修复.
1.2 主要贡献
本文主要贡献如下:
(1)对多区间速度约束以及修复结果进行了定义.本文所提的速度约束不仅仅局限于单一的最大最小速度范围,而是进一步给出了多个速度区间,使得约束更具体、更精确.修复结果的定义具体到给定窗口内,在应用时可灵活扩展到整条时间序列,进而使得修复方法具有更广泛的适用性;
(2)提出了基于多区间速度约束的时间序列修复方法,并给出了相应的具体算法.通过多区间速度约束,给出了修复对象点的修复范围以及修复候选点,并基于各修复候选点对其给定窗口内的后续时刻产生更加具体的修复范围,从而对后续修复候选点进一步进行筛选,以确定最终的修复候选点.最后对给定窗口内各时刻所确定的候选点基于图进行存储,以便于使用动态规划的方法进行修复;
(3)针对多区间速度约束的动态规划修复方法提出了相应的理论及其证明,为修复方法提供理论支持.理论1 表明:在修复候选点内可以找到一条最优修复路径,使得窗口内的修复距离和最小.此外,当后续点对当前点所生成的修复候选点不在最终的修复范围内时,理论2 也表明,可以选择相应的约束点作为新的修复候选点以保证最小的修复距离;
(4)提供单区间特例下速度约束动态规划修复与SCREEN 方法的分析比较.单区间特例下,在约束范围的确定以及修复候选点的确定方面,本文所提出的多区间速度约束方法与SCREEN 方法所得到的结果一致.而由于多区间方法在所给定的候选点内根据动态规划方法选取最优修复路径,所以本文所提出的修复方法将等同或优于SCREEN 方法;
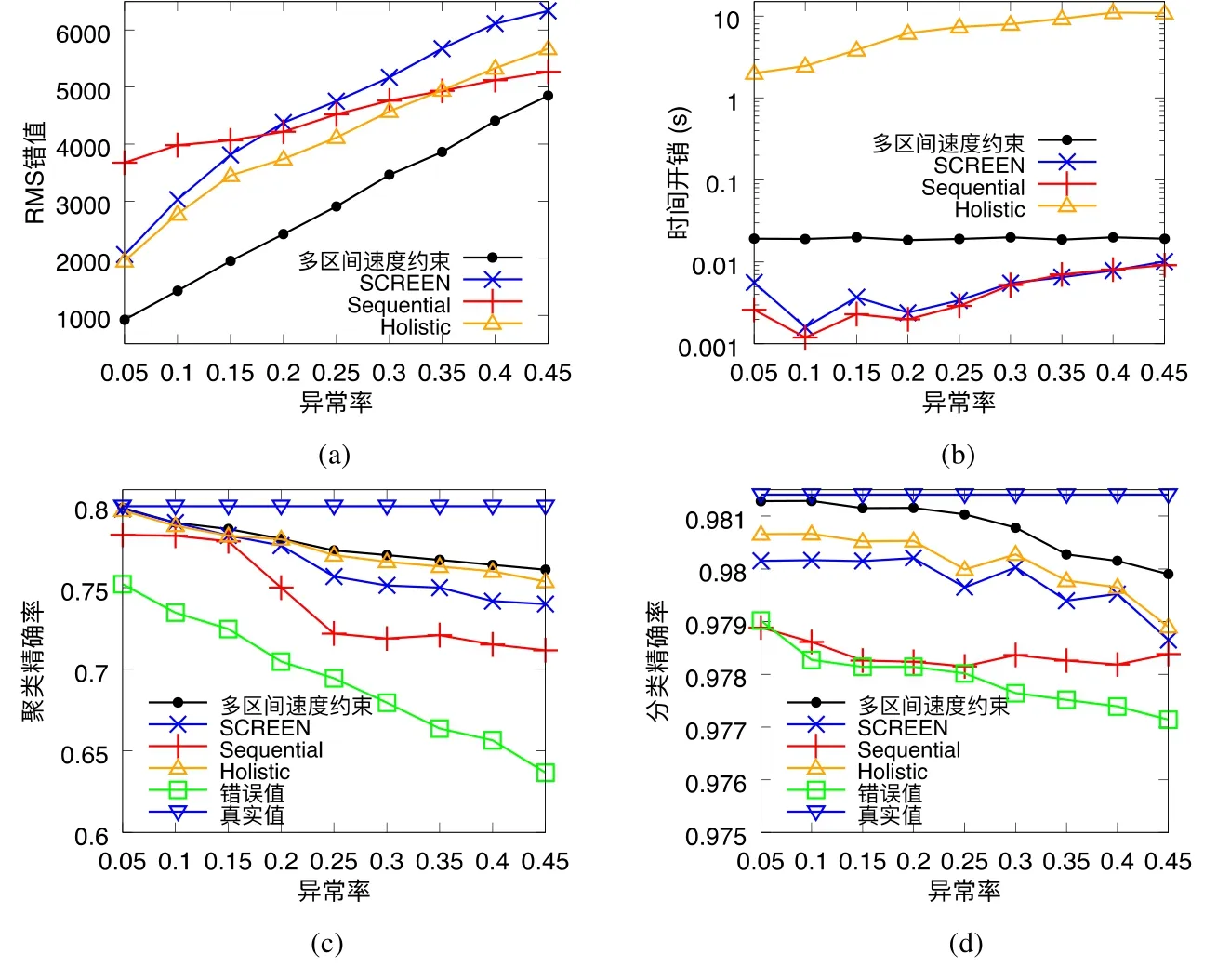
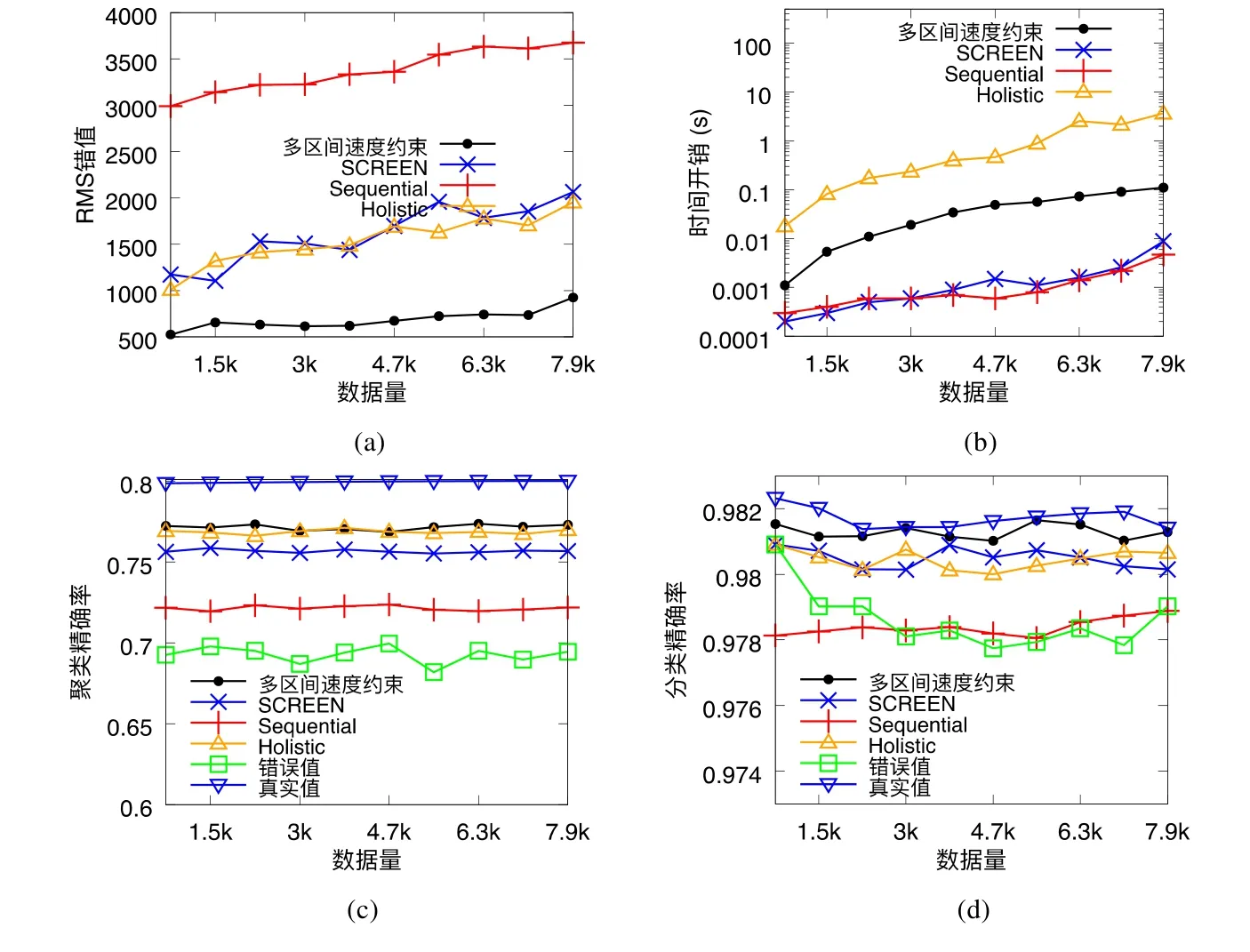
(5)采用一个人工数据集、两个真实数据集以及一个带有真实错误的数据集在RMS 错值、聚类及分类精确率及时间开销方面进行了实验,并与包括SCREEN 在内的多种现有相关方法进行了对比.结果表明:本文所提出的多区间速度约束方法在修复效果方面表现最优,同时在时间开销方面有着较好的权衡.此外,本文采用了多个带有分类标签的时序数据集在分类精确率上进行验证,从精确率结果来看,多区间速度约束方法可为后续包括数据分析以及人工智能在内的研究处理提供更优秀的数据支撑.
1.3 论文结构
本文第2 节给出本文研究相关的基础定义,对时间序列、多区间速度约束以及修复结果进行解释,并提供问题形式化定义即修复条件和修复目标.第3 节提出具体基于多区间速度约束的动态规划修复方法,包括具体方法描述、理论证明、特例分析以及具体算法等.第4 节通过一个人工数据集、两个真实数据集和一个带有真实错误的数据集,在修复效果和时间性能,以及聚类和分类精确率方面与现有方法进行对比分析,并通过多个数据集,在分类精确率上与现有方法进行比较验证.在第5 节中对相关工作进行介绍.最后,在第6 节对本文的工作进行分析总结.
2 基础定义
作为大数据技术及人工智能技术的数据支撑,工业大数据正成为数据相关研究领域的热点.本文主要研究工业数据中的时间序列数据,为便于叙述,本节将对时间序列、时间戳、速度约束、多区间速度约束以及修复结果等进行定义.
2.1 时间序列定义
时间序列指一系列包含时间戳的数据点,具体而言,在一条数据序列x=x[1],x[2],…中,数据点x[i]指第i个数据点,每个数据点x[i]都具有一个时间戳t[i].简便起见,下文中将x[i]简写为xi,t[i]简写为ti.
2.2 多区间速度约束定义
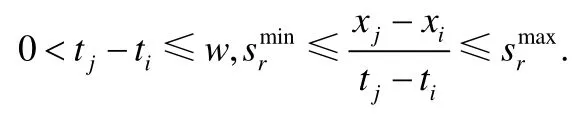
如图3 所示,在给定窗口w中,给定速度约束区间S包括两个约束区间,数据点对(x1,x2)满足速度约束区间,即
同理,(x1,x3)满足速度约束区间.因此,上述两对数据点均满足多区间速度约束S.而(x1,x4)既不满足s1也不满足s2,即数据对(x1,x4)不满足多区间速度约束S.
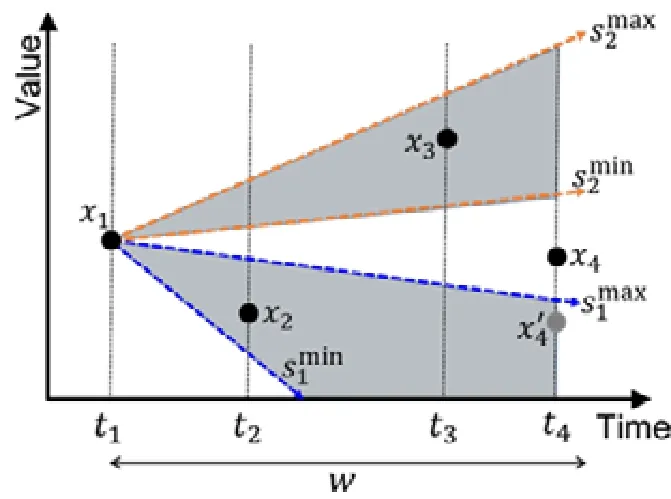
Fig.3 Example of multi-speed图3 多区间速度约束示例
2.3 修复结果定义
修复结果x′指在给定窗口w内,将时间戳ti上的数据点xi修复为,修复后时间戳不变,即.根据数据修复中的最小修复原则[2],最终的修复距离可定义为
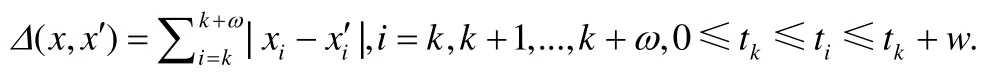
如图3 所示,x4修复为,时间戳依旧为t4,该窗口内最终修复距离为
2.4 问题定义
给定一个时间序列x,时间窗口w,窗口内共ω+1 个数据点,窗口起始点xk,窗口内各xj点的速度约束范围以及多区间速度约束S={s1,s2,…,sm},,其中,r=1,2,…,m.多区间速度约束修复指:在窗口w内找到一个修复结果x′,使得修复后窗口内各点满足多区间速度约束,同时修复距离最小,即:

其中,窗口内各xj点的速度约束范围通过xk点之前且在xj点同一窗口内的其他点进行多区间速度约束得出,若xk点前无数据点与xj点共一窗口,则不限定xj的速度约束范围,具体方法可见第3.1 节.
3 动态规划修复方法
3.1 速度约束范围的确定
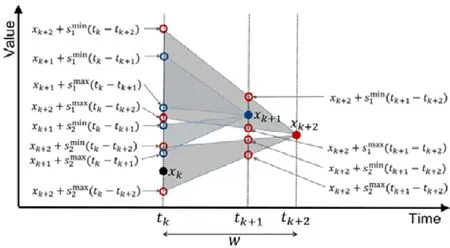
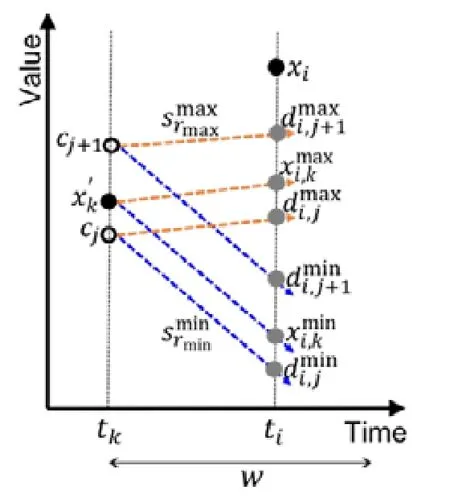
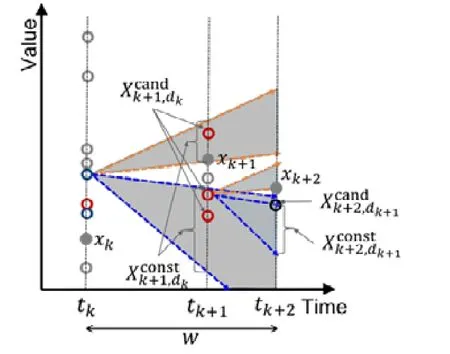
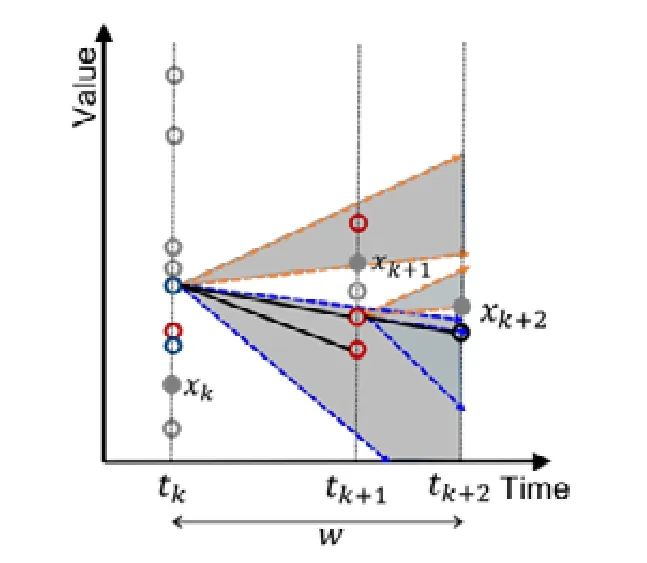
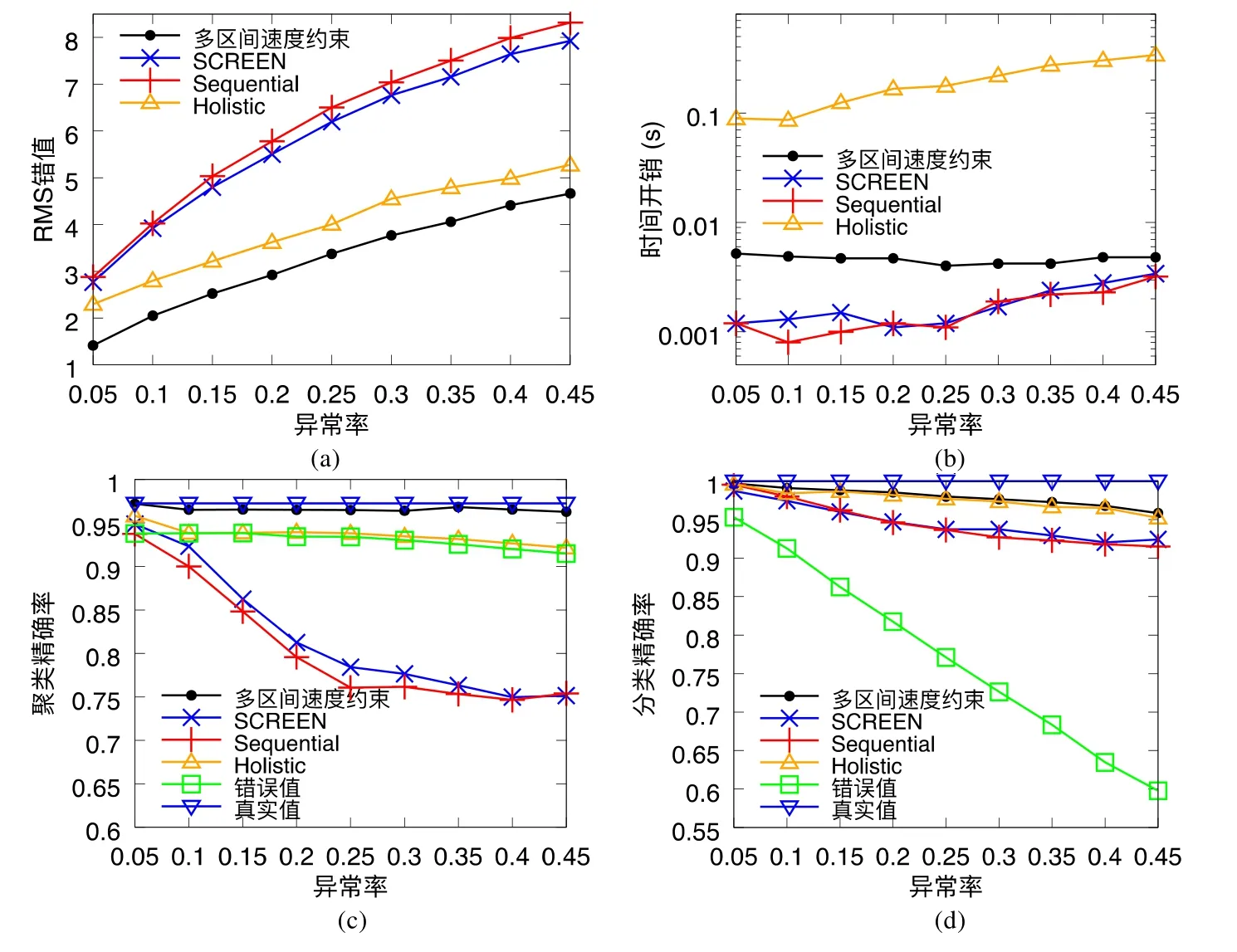
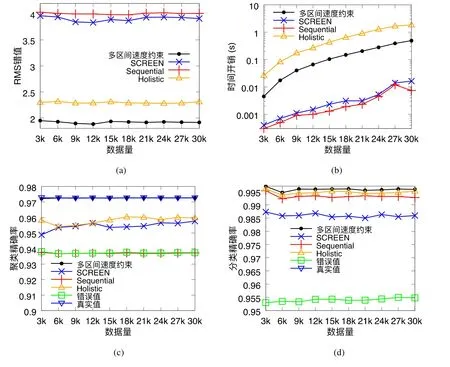
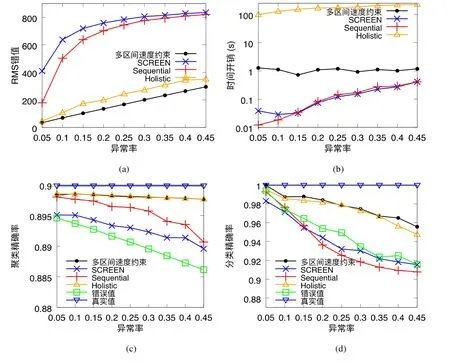
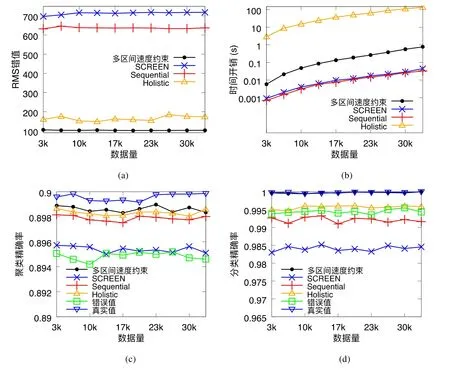
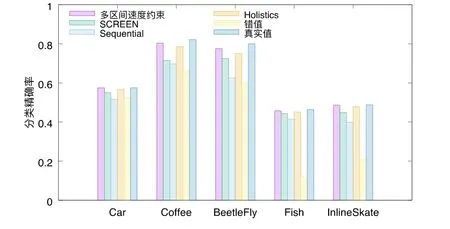
给定多区间速度约束S,窗口w,窗口内起始数据点xk以及窗口内各点xk,xk+1,xk+2,…,xk+ω,0 为更加清晰地叙述多区间速度约束方法,本节先对数据点xj进行研究,通过其同一窗口内且非给定窗口w内的其他各数据点xi(tj−w≤ti xk同一窗口内的先前点(i=k−1,k−2,…,k−nk,即:当xk为窗口内最后一个点时,为该窗口内第1 个点,≤w),将根据公式(1)、公式(2)对xk点生成速度约束范围,并根据公式(3)对各点所生成的约束范围取交集产生速度约束范围最终根据公式(4)形成xk的多区间速度约束范围集合如图4 所示,灰色区域即为xk的多区间速度约束范围集合 类似的,xk+1同一窗口内(除去给定窗口w所包含点)的先前点ix′(i=k−1,k−2,…,k−nk,即:当xk+1为窗口内最后一个点时,为该窗口内第1 个点,≤w)将对xk+1点生成速度约束范围,如图4蓝色区域所示. Fig.4 Range of multi-interval speed constraints图4 多区间速度约束范围 xk+2同一窗口内(除去给定窗口w所包含点)的先前点ix′(i=k−1,k−2,…,k−nk+2,将对xk+2点生成速度约束范围.在图4 示例中,xk+2同一窗口内的前述点均在给定窗口w内,所以此时不限定xk+2的速度约束范围. 以此类推,得出窗口w内所有点(xk,xk+1,xk+2,…,xk+ω)的速度约束范围: 1.消化道。①寄生于小肠的有:猪蛔虫、兰氏类圆线虫、蛭形巨吻棘头虫、姜片吸虫和猪等孢球虫。其中猪蛔虫的危害和流行最为严重。②大肠内寄生的有:结节虫(食道口线虫)、鞭虫(毛首线虫)和结肠小袋虫,后者多发于南方且人畜共患。③ 胃内有胃圆线虫,但危害较轻。 通过观察数据点与速度约束之间的关系可以发现,速度约束S可以与数据点xi(tk≤ti 给定窗口w内的xk后续点xi(xk+1,xk+2,…,xk+ω),tk 同理,该窗口内的数据点xk+1可由其后续点(xk+2,…,xk+ω)生成候选点集.以此类推,可得到窗w内各数据点xi(i=k,k+1,…,k+ω)的修复候选点集Xi,其中,xk+ω的修复候选点集Xk+ω中只有数据点xk+ω本身,如图5 所示. 如图6 所示,空心点为上述方法所求得的候选点,实心点为原数据点,其中:灰色点为不在约束范围内的无效候选点,其他点为有效候选点. Fig.5 Capture of repairing candidate points in a given window图5 给定窗口内各时刻修复候选点的生成 Fig.6 Obtain candidates set Xi according to range 图6 根据修复候选范围筛选修复候选点,得到集合Xi 理论1.在多区间速度约束下,一定可以在xk及其修复候选点中找到关于xk的最优修复解 证明:令ω=|{i|tk (1)若修复后xi未改变,即,此时xi点修复距离为0,如图8 所示; Fig.7 Impossible case of smaller than the minimum candidate c1,图7 小于最小候选点, Fig.8 between two continuous candidates,,without moving xi图8 介于两相邻候选点之间,无需修复 Fig.9 between two continuous candidates,图9 介于两相邻候选点之间, Fig.10 between two continuous candidates,图10 介于两相邻候选点之间, 为计算窗口内总修复距离,可以对上述情况(2)和情况(3)中的xi进行计数. (a)当情况(2)和情况(3)中xi的个数相同时,选择cj,cj+1中与xk距离更近者作为.当选择cj时,相应的总修复距离为 Δ(x,x′)=Δ(x,x′)−(−cj)<Δ(x,x′);当选择cj+1时,相应的总修复距离为 (b)当情况(2)中xi的个数大于情况(3)中xi的个数,选择cj+1作为相应的总修复距离为 (c)当情况(2)中xi的个数小于情况(3)中xi的个数,选择cj作为相应的总修复距离为 类似地,窗口内其他点xi(xk+1,xk+2,…,xk+ω),tk 由上述内容可知:在以xk为起点的窗口w中,每一个数据点xi均可获得一个给定速度约束范围内的修复候选点集合,令该集合内候选点个数为ηi. 如第3.1 节所述,给定多区间速度约束S、窗口w以及窗口内起始数据点xk,窗口内各数据点xj(tk≤tj≤tk+w)均可与其同一窗口内前述各数据点xi(ti xi的每个修复候选点ci,di均可根据公式(8)、公式(9)对同一窗口w内的后续点xj产生速度约束范围 其中,tk≤ti 其中,tk≤ti 理论2.在以xk为起点的窗口w中,若数据点xj在速度约束范围中无修复候选点,则可指定距离原xj点最近的速度约束点作为修复候选点,其中,速度约束点指上述中对xj点所确定的速度约束范围边界点,此时修复距离最小.修复候选点集合更新为如下 同理,此修复候选点对后续点产生的修复范围中若包含已有候选点,则依旧可根据该候选点选择最优修复路径;反之,若已有候选点未在该修复范围之内,则可按理论2 生成后续点的修复候选点,且该条路径的修复距离最小. 综上所述,本理论所确定的修复候选点中存在一条最优修复路径,使得修复距离最小.□ 如图11 所示:从tk时刻开始,对于数据点xi(tk≤ti Fig.11 Obtain candidates sets according to ranges图11 根据修复候选范围筛选修复候选点,得到集合 Fig.12 Generation of edges for repairing path图12 修复路径边生成 Fig.13 Graph of repairing path图13 修复路径图 本节将给出多区间速度约束下的特例情况,单区间速度约束,即只有一个速度约束区间,其中,r=1.由于SCREEN 方法同样基于速度约束,本节将针对二者进行分析比较. • 速度约束范围的确定 由于只存在一个速度约束区间,如第3.1 节所述,xk同一窗口内的先前点(i=k−1,k−2,…,k−nk)将对xk及其同一窗口w内的所有后续点xj(xk+1,xk+2,…,xk+ω)生成相应的速度约束范围,如图14 所示.该速度约束范围与SCREEN 方法中点所生成的速度约束范围相同. Fig.14 Special case of single interval speed constraint图14 单区间速度约束特例 • 修复候选点的确定 与多区间速度约束方法相同,在单一速度区间下,给定窗口w内的xk后续点xi(xk+1,xk+2,…,xk+ω,tk • 修复路径图的确定 与多区间方法相同,在单一速度区间下,窗口w内的每一个数据点xi均可获得一系列给定速度约束范围内的修复候选点.每一个修复候选点均可对同一窗口内的后续点产生速度约束范围,该速度约束范围与SCREEN方法中的速度约束范围相同.在该速度约束范围下,对窗口w内各时刻候选点的选择可形成一条修复路径.由于速度约束范围相同,那么所确定的修复候选点也与原SCREEN 版本中的修复候选点相同.因此,在上述各修复候选点所形成的修复路径中,必有一条与原SCREEN 版本中的修复路径相同,而本文根据动态规划方法选择了最小修复路径,所以本文选择的修复路径一定优于或等于SCREEN 方法中的修复路径. 本文根据上述修复方法提出了算法1. 算法1.基于多区间速度约束的动态规划修复方法. 输入:顺序时间序列x,时间窗口w,起始数据点xk,多区间速度约束S; 输出:修复后的时间序列x′. 如前文所述,在算法1 中,第1 行~第18 行主要用于初步确定修复候选点及速度约束范围.其中,第5 行~第10 行可以依据公式(1)~公式(4)对给定时间窗口w内的各数据点xi通过其同一窗口且在给定窗口w外的前述xj点生成相应的多区间速度约束范围集合;第11 行~第17 行可以依据公式(5)~公式(7)对给定时间窗口w内的各数据点xi通过该窗口w内的后续xj点及上述约束范围集合生成xi点的修复候选点集合Xi. 第19 行~第36 行主要用于确定修复路径图.其中,第28 行及第29 行依据公式(8)、公式(9)通过各时刻候选点生成窗口w内后续各时刻点的速度约束范围,并结合上述约束范围集合生成新的约束范围;第30 行~第33 行则根据新的约束范围筛选出各修复候选点约束下的后续时刻的修复候选点,并形成相应的修复路径边,同时赋予边的权重.最终,通过第37 行的动态规划方法求解得出最优修复路径. 由前述定义可知,窗口内数据点的个数最多为w,第1 行~第18 行初步确定修复候选点所需时间为O(w2).在窗口内所产生的修复候选点总数最多为(w−1)×r+1,其中,r为速度约束区间的个数.因此,第19 行~第36 行确定修复路径图所需时间为O(w2×((w−1)×r+1)).结合动态规划所需时间O(((w−1)×r+1)2),整体算法时间复杂度为O(w3×r).作为局部定义算法,本文所提出的多区间速度约束方法可以较为快速地对大数据进行修复,为后续的数据分析以及人工智能研究提供数据基础. 为验证本文所提出的多区间速度约束方法,本节将选择多个数据集,根据相应的评价标准进行实验评估,同时将实验结果与多个现有方法进行对比.具体实验环境、实验数据集、评价标准、现有对比方法以及实验结果如下所述. • 实验环境 本文使用JAVA 语言在如下环境下对各部分内容进行实现,处理器为3.1GHz Intel Core i5,内存为16GB 2133MHz LPDDR3. • 实验数据 本文采用一个人工数据集和两个真实数据集进行实验.人工数据集包含30 000 个数据点,其速度约束区间主要在[−10,−8]以及[0,2]之间.真实数据集1 为车辆油耗数据,共34 220 个数据点.如第1.1 节例1 所述,数据主要体现耗油和加油两种行为:考虑到车辆行驶过程中油箱的振荡,其耗油速度区间设置为[−1,1];而加油行为则会使油位骤然上升,可将加油速度区间设置为[10,70].真实数据集2 为GPS 轨迹数据,共7 962 个数据点,主要采集了个人步行轨迹以及汽车行驶轨迹,结合实际情况以及数据采集信息,步行速度区间为[0,10],汽车行驶速度区间为[30,100].上述3 个数据集均由无错值的数据点构成,本文采取文献[4]中所提出的方法,随机生成新的数值作为错值来代替原有真值,以形成异常数据点.如下述实验结果所示,异常率0.1 表示有10%的数据点被随机替换为异常值.在真实数据油耗集中,所注入的数据值可能会小于0,此数值为异常数据,因为油箱内的油位最小值为0,不可能为负数.同理,所注入的数据值可能会有大于70 的情况,根据本真实数据值的情况,油箱内油位最大值为70,超出该值数据可视为异常数据.当注入数据值在[0,70]范围内时,由于绝大部分情况下该随机注入的数据值无法与同一时间窗口内的其他点形成给定阈值范围内的数据变化速度,此注入的数据值仍可视为异常值.同理,在GPS 数据集以及人工数据集中,随机注入的数据值可视为异常值.同时,本文使用了海拔数据进一步验证多区间速度数据方法对真实异常值的修复作用.该数据集为地铁地面轻轨上行驶过程中所采集的海拔数据.观察所采集的真实数据发现:该数据具有较大的异常,某些数据点在1s 之内的海拔变化甚至会高达14m.经统计,该数据集共有1 398 个数据点,其中有218 个点为异常数据点.经过整体数据分布情况以及合理性分析,本文选取[−2,1.61]以及[1.9,2]作为该数据的速度约束区间.此外,为进一步验证本方法为后续数据分析及人工智能所提供的帮助,本文选取了 UCR Time Series Classification Archive(http://www.cs.ucr.edu/~eamonn/time_series_data/)中的5 个数据集,包括数据集Car,Coffee,BeetleFly,Fish 以及InlineSkate,以验证本方法下修复结果的分类精确率. 本文采用RMS错值[5]作为修复结果评价标准.令xtruth作为时间序列的真值,xrepair作为修复的时序数据结果.为了评估修复结果与真值之间的相似程度,令Δ(xtruth,xrepair)作为真值xtruth与修复结果xrepair之间的距离,Δ(xtruth,xrepair)越小,修复结果与真值越相近,即修复结果越精确. 此外,考虑到修复后的数据将在后续的数据分析及人工智能方面起着基础支撑性作用,本文还提出了各数据集进行修复后的聚类及分类结果.本文采取DBSCAN[6]方法对各修复结果进行聚类分析,并选用KNN 方法[7]对各修复结果进行分类,采用了k折交叉验证[8]方法.本文所使用的聚类及分类精确率[9]如下公式所述: 本文新提出的多区间速度约束方法将与现有的多种修复方法进行比较,包括基于单区间速度约束的SCREEN 方法、基于顺序依赖Sequential Dependency[10]的修复方法以及基于否定约束的全局Holistic[11]修复方法. 本文选择3 个数据集来对修复方法进行验证,并对各数据集提供了多种修复方法在不同异常率(异常数据点数/总数据点数)下及不同数据量下的RMS 错值结果、时间开销结果以及聚类与分类精确率结果.同时,本文提供了具有真实异常的海拔数据集,并根据多种方法进行修复得出修复后的RMS 错值结果、时间开销结果以及聚类与分类精确率结果.此外,本文还通过UCR 时序数据中的5 个数据集对上述各修复方法进行了分类精确率验证.具体实验结果如下文所述. (1)人工数据集 由图15(a)可发现,本文所提出的多区间速度约束修复方法所表现出的修复效果在各异常率下均优于其他修复方法.其结果趋势与全局修复Holistic 方法相似,但明显优于Holistic 方法. 为更加直观地验证本文所提方法对数据分析及人工智能方面的影响,图15(c)及图15(d)提供了聚类及分类精确率.观察结果图可发现:SCREEN 方法及Sequential 方法随着异常率的增加,其聚类效果显著下降,甚至远低于未经修复的错值数据聚类结果;而本文方法则表现出了最优的聚类结果,与真实结果较为接近,且明显高于全局修复Holistics 方法.在分类结果方面,与RMS 错值结果类似,多区间速度约束修复方法与全局Holistic 方法随着异常率的增加而远优于SCREEN 方法及Sequential 方法;同时,多区间速度约束方法整体体现出最优的修复效果.该实验结果表明:相对于其他方法,本文所提出的多区间速度约束方法可以对数据分析与人工智能技术提供更为精确的数据基础. Fig.15 Varying rates of anomalies over synthetic data图15 人工数据集中不同异常率下的修复效果 在时间开销方面,由图15(b)可知,本文方法远低于Holistic 方法.且在不同的异常率下,本文方法时间开销较为稳定.此外,虽然SCREEN 方法以及Sequential 方法的时间开销较低,但本方法在各异常率下的RMS 错值均远低于上述两种方法.进一步观察可发现:随着异常率的上升,相对于SCREEN 与Sequential 方法,本文所提出的多区间速度约束方法在RMS 错值及聚类分类精确率方面表现出更加突出的优越性. 关于不同数据量下的修复结果,观察图16 可以发现,与不同异常率下的修复结果较为一致,多区间速度约束方法在RMS 错值方面有着最优的修复效果,且多区间速度约束方法与全局Holistic 方法在RMS 错值方面远低于SCREEN 方法及Sequential 方法. Fig.16 Varying data sizes over synthetic data图16 人工数据集中不同数据量下的修复效果 在聚类及分类精确率方面,本实验选取了异常率为0.05 的数据.在聚类精确率方面,在不同数据量下的修复结果中,Sequential 方法表现出了最差的聚类精确率;而多区间速度约束方法有着最高的聚类精确率,且与正确数值下的聚类结果高度接近.在分类精确率方面,SCREEN 方法表现出了最差的分类精确率,而多区间速度约束方法同样有着最高的分类精确率.同时,本可扩展性实验结果也表明:在不同的数据规模,甚至是大数据规模下,本文方法可以提供较为优质的数据支撑.此外,在时间开销方面,本文所提出的多区间速度约束方法低于全局Holistic 方法,在修复效果与时间开销方面有着较好的权衡. (2)油耗数据集 关于真实油耗数据集在不同异常率下的实验,由图17(a)可发现:与人工数据集较为相似,本文所提出的多区间速度约束修复方法所表现出的修复效果在各异常率下均优于其他修复方法,尤其在异常率大于0.1 的情况下,远优于SCREEN 方法以及Sequential 方法.结合RMS 错值与图17(b)时间开销结果来看,本文所提出的多区间速度约束方法较好地权衡了修复效果与时间开销之间的关系,即在时间开销远低于Holistic 方法的前提下,给出了优于该方法的修复效果. 此外,在聚类精确率方面,本文所提多区间速度约束方法远高于未经修复的错值数据聚类结果;且随着异常率的增加,其聚类精确率与Holistics 方法相似,远高于SCREEN 方法及Sequential 方法所得到的修复结果.值得一提的是:在分类精确率方面,SCREEN 方法以及Sequential 方法修复后的结果甚至要低于未修复的错值数据;而本文所提的多区间速度约束方法以及全局Holistic 方法则远高于未修复的错值数据,尤其是在异常率为0.05时,极其接近真实值的修复结果. Fig.17 Varying rates of anomalies over oil data图17 油耗数据集中不同异常率下的修复效果 与人工数据集实验类似,在不同的异常率下,本文方法时间开销也较为稳定;而SCREEN 与Sequential 方法则随着异常率的增加,其时间开销呈明显上升趋势.综合来看,本文所提出的多区间速度约束方法更适用于后续的数据分析及人工智能技术,可以在较短的时间内较为高效地对时间序列进行清洗以提高数据质量,从而为数据分析及人工智能技术提供更精确的数据基础. 在基于异常率的实验之外,本实验提供了如下关于真实油耗数据集在不同数据量下的实验.由图18(a)可以发现:与异常率实验较为一致,多区间速度约束修复方法在各数据集大小下均表现出最优的修复结果.具体从图18(c)聚类精确率上来看:在不同的数据量下,本文方法所得到的修复结果相较于其他方法有着最高的聚类精确率,且修复结果较为稳定,有着较好的可扩展性.从图18(d)分类精确率结果上来看:在0.05 的异常率下,本文所提出的多区间速度约束方法表现出了极为优秀的分类结果,其各数据规模下的修复结果与真实值高度相似且接近于1.结合图18(b)可知:在时间开销稍高于SCREEN 方法以及Sequential 方法的前提下,本文方法RMS 错值远低于上述两种修复方法.同时,在RMS 错值较低于Holistic 方法的前提下,本文方法时间开销远低于该方法,整体相差两个数量级. Fig.18 Varying data sizes over oil data图18 油耗数据集中不同数据量下的修复效果 (3)GPS 数据集 观察图19 中关于真实GPS 数据集在不同异常率下的实验结果可以发现,该实验结果在时间开销上与人工数据集以及真实油耗数据集较为相似.关于RMS 错值实验结果,观察图19(a)可发现:现有其他方法在此数据集修复结果上较为集中,且多区间速度约束方法明显优于其他各方法.值得说明的是:由于在上述人工数据集以及真实油耗数据集中,序列为时间等间隔数据,而Sequential 方法是考虑连续两个数据点之间的数值距离约束,所以此时Sequential 方法与SCREEN 速度约束方法有着较为相似的结果及趋势.而在此GPS 数据集实验中,数据并非等时间间隔序列,所以上述两种方法实验结果相对存在较大的差异. 由图19(c)可知:在聚类精确率方面,本文所提方法随着异常率的提高,其聚类效果远高于SCREEN 方法、Sequential 方法以及未经修复的错值数据,且与全局修复Holistics 方法也拉开了一定的距离.同样,图19(d)也清晰地表明了本文所提出的多区间速度约束方法在分类精确率上呈现出最优的修复效果,尤其在异常率低于0.25 时,其精确率与真实时序数据的分类精确率较为贴近,且远高于其他修复方法,尤其是Sequential 修复方法. 为了更好地体现各方法的修复效果,本实验选取GPS 数据集在0.05 异常率下进行可扩展性实验,并提供了在不同数据量下的实验结果.由图20(a)可发现:随着数据量的增加,各方法在RMS 错结果值上均有着或多或少的上升.而在各方法中,多区间速度约束方法下的RMS 错值结果值增幅最小,这也体现出该方法具有最佳的可扩展性. 在分类精确率方面,本文所提出的多区间速度约束方法也呈现出了最优的分类精确率,同时,Sequential 方法则有着最低的精确率,甚至在某些数据量下(如数据量小于2.3k 时),其分类精确率远低于未经修复的错值数据,与不同异常率下的修复结果及不同数据量下的RMS 错值结果较为一致.而由于在0.05 异常率下的多个方法修复结果的聚类效果较为接近,所以本文进一步选取异常率为0.25 的数据来进行聚类结果的可扩展性实验,以使各方法下的聚类精确率可以较为清晰地呈现.从图中可以发现:本文方法在较少的时间开销下,其聚类精确率与全局修复Holistic 方法较为相似,且较高于Holistics 方法,远高于Sequential 方法及未经修复的错值数据. Fig.19 Varying rates of anomalies over GPS data图19 GPS 数据集中不同异常率下的修复效果 Fig.20 Varying data sizes over GPS data图20 GPS 数据集中不同数据量下的修复效果 关于时间开销方面,由图20(b)可知:与真实油耗数据集实验相似,多区间速度约束方法在保持最低RMS 错值的前提下,其时间开销处于可接受范围,整体低于全局Holistics 方法1 个数量级. (4)海拔数据集 为进一步佐证本文所提多区间速度约束方法在真实数据集中的实用性,本文针对具有真实异常的海拔数据集使用多种修复方法进行实验,最终得出其RMS 错值结果、聚类与分类精确率结果以及时间开销结果,见表1.从表1 中可发现:在RMS 错值方面,本文所提出的多区间速度约束方法表现出了最优的修复结果,与Holistic方法、SCREEN 方法以及SWAB 方法相比,本文方法RMS 错值更低,修复结果更精确,且远优于Sequential 方法;在聚类精确率方面,相较于其他各修复方法,多区间速度约束也呈现出了较好的结果;在分类结果方面,本文所提多区间速度约束方法也优于其他各方法,更接近于正确值所达到的分类精确率;此外,在时间开销方面,本文所提方法也达到了最少的时间开销,远低于具有较优修复结果的Holistic 方法. Table 1 Altitude dataset with real anomalies表1 带有真实错误的海拔数据集修复效果 (5)UCR 数据集 为了进一步验证各修复方法在分类效果上的表现,从而为后期包括数据分析及人工智能在内的多种应用做好数据支撑,如前所述,本文选取多个具有分类标签的时序数据集,以更全面广泛地验证本文所提的多区间速度约束方法对后续数据应用所产生的影响.由图21 发现:在不同数据集下,多区间速度约束方法均呈现了较好的分类结果,远高于未经修复的错值数据分类结果,同时与真实值分类精确率较为接近.图中5 个数据集真实数据分类数目有一定的差异,其中,Car 数据集有4 个分类标签;Coffee 及BeetleFly 数据集有2 个分类标签,因此在这两个数据集中,整体分类精确率较高;与之相反,Fish 及InlineSkate 数据集中有7 个分类标签,因此如图所示,其整体分类精确率偏低.然而在这两个数据集中,各方法修复后的分类结果均远高于未修复的错值分类结果,这也进一步表明,数据应用前期的数据清洗修复等步骤对后续的数据分析及人工智能过程有着至关重要的作用. Fig.21 Classification accuracy under different UCR datasets图21 UCR 数据集分类精确率 随着大数据和人工智能技术的深入发展,作为其技术支持与基础的数据管理与分析技术也日益成为相关领域研究热点问题.为了进一步推动数据管理与分析技术,优化大数据和人工智能的产出成果,减少因数据问题而对后续分析研究形成的限制,数据质量问题受到了越来越多的关注.Ji 等人[12]提出了查询容错等机制,但该机制必须在容错效果、性能和实现成本之间进行折衷,且并未对数据查询等范围外的数据使用进行处理说明.此外,诸多业内研究者针对数据异常问题提出了多种检测及修复技术. 基于平滑的修复方法指使用数据平滑技术来减少异常点.基于平滑修复可以减少噪声点,使数据变化趋势更顺畅平滑,直觉上,该类平滑后的数据有着更少的异常点.其中,SWAB 平滑算法[13]基于线性插值[14]以及回归技术[15]对时间序列数据进行清洗,由于该算法可以对时间序列进行分段,因此该算法可以支持时间序列数据进行在线清洗.此外,移动平均方法也常用于时间序列数据平滑修复.简单移动平均值(SMA)是最后k个数据的未加权平均值,该算法以此值来对下一个数据点进行修复.而加权移动平均值(WMA)则对窗口中不同位置的数据点添加了权重设置,例如距离目标数据点越远的数据权重越低等.相应地,指数加权移动平均值(EWMA)[16]随时间距离增加添加指数递减的权重,以适用于非稳态的时间序列[17−19]. 基于平滑的修复方法存在较大的修复局限性,为保障时间数据序列的平滑性,平滑修复方法会将异常点附近多个原本正确的真值数据反而过度修复为错值数据,异常点会极大地影响修复结果的精确性. 通常来说,大多数数据在点与点之间具有一定的约束依赖.在关系型数据库领域,有很多基于完整性约束的清洗算法.一些数据约束规则,例如函数依赖(functional dependency,简称FD)[20,21]等,可用于数据清洗修复相关问题中.该类方法通过求解数据的最小修复进行数据清洗,相应的清洗结果会满足所给定的函数依赖约束规则.而由于约束关系适用于任何一对元组,因此具有最小修改的修复问题通常被认为是NP 难题[22].考虑到这一问题,Beskales 等人[23]提出了基于采样的数据清洗方法,其基本思想是,从数据修复候选集中抽取部分样本来进行数据清洗.此外,基于FD 约束存在的另一个问题是,一些真实数据集中无法寻取绝对的FD 约束.因此,Bohannon等人[24]在基于函数依赖的清洗修复中引入了条件概念,即利用条件函数依赖(conditional functional dependency,简称CFD)[25,26]作为约束进行数据清洗.然而,由于该方法所需要的约束规则较为繁琐庞大,所以所形成的算法在时间开销上不甚理想.在如今大数据及人工智能背景下,该方法无法快速而准确地为后续相关技术操作提供优质的数据支持. 一般情况下,在时间序列数据中,数据值大多为具体的数据,而FD,CFD 等数据约束规则需要遵循严格的相等关系,所以基于上述约束的修复方法在时间序列数据中难以产生较好的清洗修复结果.基于此,Fan 等人[27]提出了匹配依赖(matching dependency,简称MD),将上述严格的相等关系进一步放宽为相似关系,即可以在约束规则的左边引入相似度度量.进一步地,Song 等人[28]提出了差异依赖(differential dependency,简称DD),在约束规则的左右两边均引入相似度度量,从而将两边的相等关系均放宽为相似关系.此外,Lopatenko 等人[29]提出了基于否定约束(denial constraint,简称DC)的规则,进而对基于DC 的数据清洗修复方法进行了研究.Chu 等人也提出了基于DC 的全局修复算法Holistic. 然而,全局修复Holistic 作为一种支持速度约束的技术,仅可用于修复一般表格数据,因此无法支持流数据的在线清洗.而现今的数据分析技术及人工智能技术等更是需要对海量数据进行处理,全局修复方法无法提供相应的技术支撑.本文提出了给定窗口条件下基于多区间速度约束的局部修复方法以支持在线清洗,作为局部方法,本文方法更有利于大数据环境下的数据清洗问题,从而更便于后续的数据管理与分析技术以及人工智能技术.因此如实验所示:与整体清洗相比,本文所提出的多区间速度约束方法最大可将时间成本降低两个数量级.此外,顺序依赖(sequential dependency)方法不能精确表达速度限制.Sequential 方法主要关注序列中两个连续数据点的差异,而当数据点之间的时间间隔不同时,Sequential 所给出的依赖并不精确.而基于速度约束的SCREEN 方法仅考虑单一区间的速度约束,当速度约束涉及多个区间时,该修复方法将由于检测修复不足或过度而无法达到较优的修复结果. 本文所提出的多区间的速度约束考虑了更具体的约束区间以得到更为精确修复结果.如第1.1 节例1 所示,车辆油位变化源于行驶耗油和补充加油两种行为,考虑到车辆及油箱振荡情况,那么油位变化速度将在[−1,1]以及[10,70]两个区间内.单区间速度约束无法表示如此精确的约束条件,进而其修复结果也将产生较大误差;而多区间速度约束方法将会对数据进行准确的约束,从而可以更广泛合理地应用.如图22 所示,本文使用多种约束方法对油耗数据集中100 个数据点进行修复.可以发现:Sequential 方法与SCREEN 方法有着一定的相似性,而由于Sequential 方法仅对连续两点之间的数据距离进行约束,SCREEN 方法对两点之间的速度(即考虑数据值及其时间戳之间的关系),所以SCREEN 方法相对更为精确.然而,由于SCREEN 方法只设置单个速度约束区间,一些正常点和异常点无法正确检测区分.当区间设置为[−1,70]时,由于15:12 时刻一个异常点的的存在,导致后续多个正确值被误修.而当区间设置为[−1,1]时,又会因为15:09 时刻的加油行为,而将后续大部分正常值误判为异常值进行过度修复.同理,若将区间设置为[10,70],几乎所有的点都会被过度修复从而对数据产生更严重的破坏.综上可知,本文所提出的多区间速度约束修复方法可以满足多速度阈值约束并给出较为精确的修复结果.此外,结合前述各数据集实验结果可知,本文方法可以在远低于Holistic 方法的时间开销下产生更优的修复结果. Fig.22 Repairing for constraint-based methods图22 基于多种约束方法下的修复效果 考虑到一般情况下时间序列中时间戳与相应数据值之间具有较强的关联性,本文提出了基于数据变化速度的多区间速度约束方法.该方法可通过多区间速度约束来获取时间序列给定窗口内各数据点的速度约束范围,进而对时序数据进行约束以检测数据的异常情况.同时,上述多区间速度约束可对窗口内各数据点通过其后续点产生相应的修复候选点,进而本文可采用动态规划方法从上述修复候选点中选取最优修复路径,从而获取修复结果,且该修复结果遵循最小修复原则.为对上述所提修复方法进行验证,本文通过一个人工数据集、两个真实数据集(油耗数据集以及GPS 数据集)以及一个具有真实异常的数据集(海拔数据集)来对本文方法及其他现有方法进行实验.由实验结果可知:与现存其他修复方法相比,本文所提出的基于多区间速度约束下的动态规划修复方法遵循最小修复原则,且可应对较为复杂的数据状况,从而在各异常率及数据量下均有着最低的RMS错值,即修复效果最佳.同时,考虑到数据质量问题将对后续的数据分析及人工智能技术产生举足轻重的影响,本文进一步使用多个数据集通过聚类及分类精确率对各方法进行了验证.在该实验结果中,本文所提多区间速度约束方法依然表现出了最优的修复效果,在各方法中分类精确率最高.此外,本方法在运行性能时间开销方面也较为理想,远低于基于约束的全局修复方法.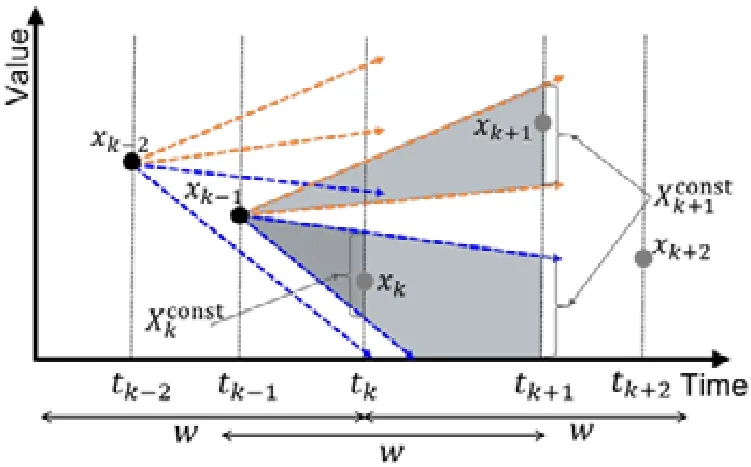
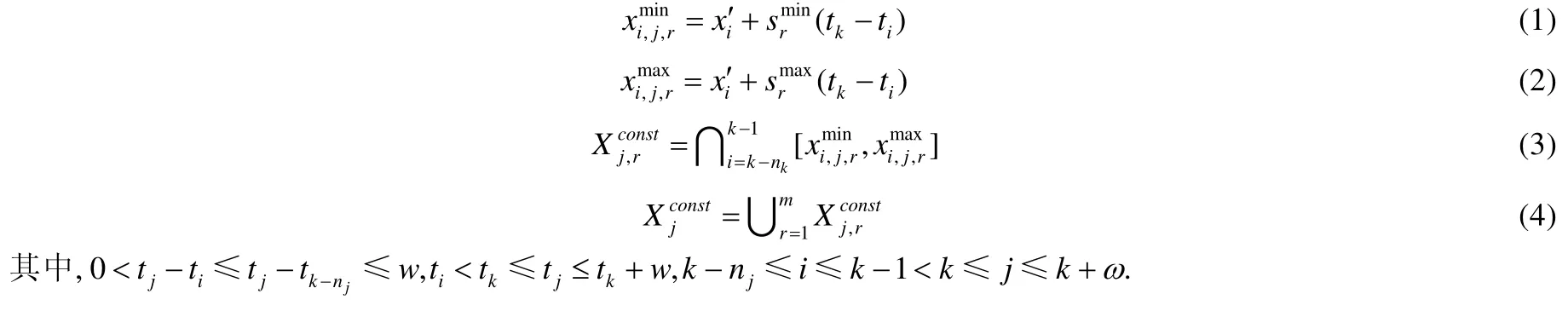
3.2 修复候选点的确定
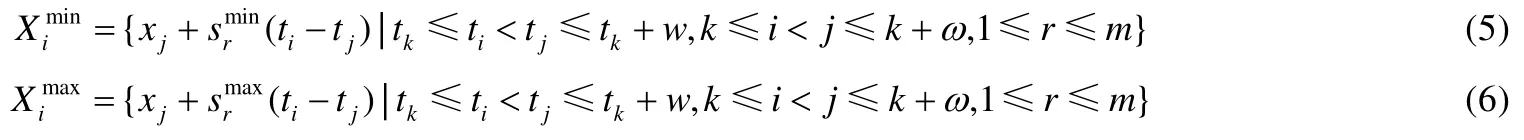
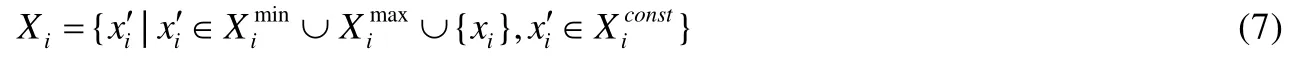




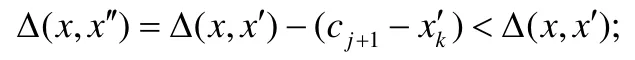

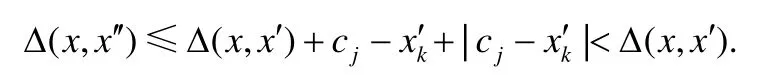
3.3 修复路径的确定




3.4 特例:单区间速度约束

3.5 算 法


4 实 验
4.1 实验设置
4.2 评价标准

4.3 现有方法
4.4 实验结果

5 相关工作
5.1 基于平滑的修复方法
5.2 基于约束的修复方法
6 结 论

