LFKT:学习与遗忘融合的深度知识追踪模型∗

李晓光,魏思齐,张 昕,杜岳峰,于 戈

1(辽宁大学 信息学院,辽宁 沈阳 110036)

2(东北大学 计算机科学与工程学院,辽宁 沈阳 110163)

在线教育系统提倡因材施教,即根据学生的知识水平为其推荐合适的学习资源[1].学生的知识水平受其学习阶段和认知能力的影响,在学习过程中不断变化.实时追踪学生知识水平,对于个性化在线教育至关重要[2,3].知识追踪(knowledge tracing,简称KT)任务主要包括:(1)通过学生的学习历史实时追踪其知识水平变化;(2)根据学生的知识水平预测其在未来学习中的表现.

传统的知识追踪技术主要有基于隐马尔可夫模型(HMM)[4]的贝叶斯知识追踪(BKT)[5].近年来,深度学习在自然语言处理[6]及模式识别[7]等任务上的表现优于传统模型.在知识追踪研究领域,亦提出了大量基于深度学习的知识追踪模型.基于循环神经网络的深度知识追踪(DKT)模型[8]采用循环神经网络的隐藏向量表示学生的知识状态,并且据此预测学生的表现.动态键-值对记忆网络(DKVMN)[9]借鉴了记忆网络(memory network)[10]的思想,用值矩阵表示学生对于各个知识点的掌握程度,并以此预测学生表现,提升预测准确度.但是以上知识追踪方法都忽略了学生在学习过程中的遗忘行为对知识水平的影响.在教育心理学领域已经有很多学者认识到人类的遗忘行为,并且探索影响人类遗忘的因素.教育心理学理论艾宾浩斯遗忘曲线理论[11,12]提出:学生会遗忘所学知识,遗忘带来的影响是知识掌握程度的下降.学生重复学习知识点的次数与距离上次学习知识点的时间间隔会影响学生的遗忘程度.教育心理学理论记忆痕迹衰退说[13]认为:遗忘是记忆痕迹的衰退引起的,消退随时间的推移自动发生,原始的痕迹越深,则遗忘的程度越低.目前,在知识追踪领域,只有少数的研究考虑了学生的遗忘行为.BKT 的扩展[14,15]考虑了艾宾浩斯遗忘曲线提到的影响遗忘程度的两个因素:重复学习知识点的次数和间隔时间.DKT 的扩展[16]考虑了学生顺序学习的间隔时间,该研究认为:学科中的各个知识点是相通的,持续的学习会降低学生对于知识点的遗忘程度.然而,以上的研究仅仅考虑了部分影响学生遗忘的信息,忽略了学生原本知识水平对于遗忘程度的影响,学生对于其掌握的知识点和没有掌握的知识点的遗忘程度不同.与此同时,由于BKT 算法与DKT 算法的局限性,以往涉及遗忘的研究或者仅考虑了学生对于单个知识点的遗忘程度,或者仅考虑了学生对于整个知识空间的遗忘程度,没有建模学生对知识空间中的各个知识点的遗忘情况.

针对于此,本文提出一种兼顾学习和遗忘的深度知识追踪模型 LFKT(learning and forgetting behavior modeling for knowledge tracing).LFKT 拟合了学生的学习与遗忘行为,实时更新、输出知识点掌握程度,并以此预测其未来表现.本文主要创新和贡献有:

(1)结合教育心理学,知识追踪模型LFKT 考虑了4 个影响知识遗忘的因素:学生重复学习知识点的间隔时间、重复学习知识点的次数、顺序学习间隔时间以及学生对于知识点的掌握程度.LFKT 根据以上信息建模遗忘行为,拟合学生因遗忘行为导致的知识掌握程度变化;

(2)基于深度神经网络技术,LFKT 设计了一个基于RNN 和记忆神经网络的知识追踪神经网络.该网络包括注意力层、遗忘层、学习层、预测层和知识水平输出层.其中:遗忘层采用全连接网络计算记忆擦除向量和记忆更新向量,用以拟合遗忘行为;学习层采用LSTM 网络,并利用学生在学习结束时的答题结果作为知识掌握程度的间接反馈.根据记忆擦除向量和记忆更新向量,获得经过遗忘后的知识掌握程度的中间嵌入,并以此作为学习层的输入,进而获得遗忘与学习相融合的知识掌握程度嵌入;

(3)通过在两个真实在线教育数据集上的实验验证结果表明:LFKT 可以有效地建模学生的学习行为与遗忘行为,实时追踪学生的知识水平,并且LFKT 模型的预测性能优于现有模型.

本文第1 节介绍知识追踪相关工作.第2 节给出相关概念和符号定义,并提出问题.第3 节详细介绍LFKT模型结构以及训练方法.第4 节给出LFKT 对比实验结果和分析.最后总结全文.

1 相关工作

知识追踪大致可以分为基于隐马尔可夫模型的知识追踪与基于深度学习的知识追踪.

贝叶斯知识追踪是典型的基于隐马尔可夫模型实现知识追踪目标的模型之一.BKT 将学生对某个知识点的潜在知识状态建模为一组二进制变量,每一个变量代表学生对于特定知识点“掌握”或“没掌握”,根据隐马尔可夫模型更新学生的知识状态,进而更新其在未来学习中的表现.在BKT 的基础上,通过考虑其他因素,提出了很多扩展方案,例如:Pardos 等人的研究[17]引入了习题难度对预测学生表现的影响;Baker 等人的研究[18]引入了学生猜测和失误对预测学生表现的影响;Khajah 等人的研究[19]将人类的认知因素扩展到BKT 中,从而提高预测精度.基于隐马尔可夫的知识追踪模型将学生对各个知识点的掌握程度分别建模,忽略各个知识点之间的关系.BKT 模型简单地将学生对于各个知识点的掌握程度分为“掌握”与“未掌握”,忽略了中间情况.

深度知识追踪是深度学习模型循环神经网络在知识追踪任务的首次尝试,将学生的学习历史作为输入,使用RNN 隐藏状态向量来表示学生的知识水平,并且基于此预测学生未来学习表现.DKT 模型无法建模学生对于各个知识点的掌握程度,仅仅可以建模学生的整个知识水平.Chen 等人的研究[20]考虑了知识点之间的先验关系,提升了DKT 的预测性能.Su 等人的研究[21]将习题文本信息和学生的学习历史作为循环神经网络的输入,利用RNN 的隐向量建模学生的知识水平,取得了较好的预测效果,但是依旧无法建模学生对于各个知识点的掌握程度.DKVMN 模型借鉴了记忆网络的思想,用值矩阵建模学生对于各个知识点的掌握程度,考察习题与各个知识点之间的关系,追踪学生对于各个知识点的掌握程度.Abdelrahman 等人的研究[22]利用注意力机制,着重考察学生作答相似习题时的答题历史,改进了 DKVMN.Sun 等人的研究[23]将学生答题时的行为特征扩展到DKVMN,从而取得更好的预测效果.Liu 等人的研究[24]利用习题的文本信息与学生的学习历史进行知识追踪.Nakagawa 等人的研究[25]用知识图建模各个知识点之间的关系,取得了良好的预测效果.Minn 等人的研究[26]根据学生的知识水平对学生进行分类,再对每一类学生进行知识追踪.Cheng 等人的研究[27]通过深度学习扩展了传统方法项目反映理论.Shen 等人的研究[28]考虑了每个学生的个性化差异,取得了很好的效果.Ai 等人的研究[29]考虑了知识点之间的包含关系,重新设计了记忆矩阵,改进了DKVMN,取得了良好的效果.关于学生遗忘行为对知识掌握状态的影响,Qiu 等人[15]考虑了学生距离上一次重复学习知识点的间隔时间,将新一天的标记加入到BKT 中,建模先前学习之后一天的遗忘行为,但是无法对较短时间的遗忘行为进行建模.Khajah 等人的研究[14]应用学生重复学习知识点的次数估计遗忘的概率,改进了BKT,提升了预测准度.Nagatani 等人的研究[16]考虑了重复学习知识点的次数、距离上一次学习知识点的间隔时间和距离上一次学习的间隔时间,改进了DKT模型,但忽略了学生原本对于知识点掌握程度对学生遗忘程度影响.

总的来说,当前的研究可以一定程度上追踪学生对于各个知识点的掌握程度,但或者忽略了学生遗忘行为,默认学生在学习间隔前后知识水平一致;或者对于遗忘行为的建模不够全面.本文所提出的LFKT 模型综合考察了影响学生遗忘程度的因素,将学生的练习结果作为学生知识掌握程度的间接反馈,建模学生的学习与遗忘行为,实时追踪学生对于各个知识点的掌握程度,预测学生未来学习表现.

2 问题定义

这里,我们定义S为学生集合,K为知识点集合,E为习题集合.每个学生单独进行学习,互不影响.学生s的答题历史Hs=[(e1,r1),(e2,r2),...,(et,rt)],其中:et为学生t时刻所做的习题;rt为答题结果,rt=1 表示答题正确,rt=0 表示答题错误.kt⊆K为习题et所涉及的知识点集合.矩阵MK(dk×|K|)为整个知识空间中|K|个知识点嵌入表示,其中,dk维列向量为一个知识点的嵌入表示.矩阵为学生在t−1 时刻的知识空间中知识点嵌入.用|K|维向量valuet−1表示t−1 时刻学习结束时学生对于各个知识点的掌握程度,其中,向量每一维的值介于(0,1)之间:值为0,表示学生对于该知识点没有掌握;值为1,表示学生对于该知识点已经完全掌握.学生在学习过程中会遗忘未复习的知识点,同时,学生在两次学习的间隔时间也会遗忘所学知识,因此,t−1 时刻学习结束时的知识水平与t时刻学习开始时的知识水平不尽相同.本文用矩阵建模学生在t时刻开始学习时的知识掌握状态.矩阵与形状相同,是由经过遗忘处理后得到.t时刻学习结束,系统获得学生答题结果,LFKT 模型根据答题结果将开始学习时知识掌握嵌入矩阵更新为学习结束时知识掌握嵌入矩阵,以此建模学习行为.预测学生在下一个候选习题et+1上的表现时,由于t时刻学习结束到t+1 时刻开始答题之间存在时间间隔,学生在时间间隔内的遗忘行为会影响知识掌握状态,因此需要根据影响知识遗忘的因素将更新为,从而预测学生答题表现.

基于以上描述,本文将问题定义为:给定每个学生的学习历史记录,实现以下两个目标.

• 跟踪学生的知识状态变化;

• 预测学生在下一个候选习题et+1上的表现.

3 方法描述

3.1 影响知识遗忘的因素

学生如果没有及时复习所学知识,就会产生遗忘,其对知识的掌握程度便会衰减.教育学理论艾宾浩斯曲线理论[11,12]表明,学生对于所学知识点的保留率受以下两方面影响:学生重复学习次数与时间间隔.时间间隔可以分为重复学习知识点的时间间隔和顺序学习的时间间隔.除此之外,教育心理学理论记忆痕迹衰退说[13]认为,学生对于知识点的掌握状态也影响着学生的遗忘程度.因此,本文考虑了以下4 个影响知识遗忘的因素.

• RT(repeated time interval):距离上次学习相同知识点的时间间隔;

• ST(sequence time interval):距离上次学习的时间间隔;

• LT(repeated learn times):重复学习知识点的次数;

• KL(past knowledge level):学生原本对于该知识点的掌握程度.

RT,ST 和LT 这3 个标量组合在一起得到向量Ct(i)=[RTt(i),STt(i),LTt(i)],表示影响学生对于知识点i遗忘程度的前3 个因素.每个知识点所对应的向量Ct(i)组成矩阵Ct(dc×|K|).本文用向量度量学生原本对于知识点i的掌握程度,并且将其作为影响学生对于知识点遗忘程度的第4 个因素(KL).将矩阵Ct与组合在一起,得到矩阵,表示4 个影响知识遗忘的因素.

3.2 LFKT模型

本文提出了一种融合学习与遗忘的深度知识追踪模型LFKT,如图1 所示.

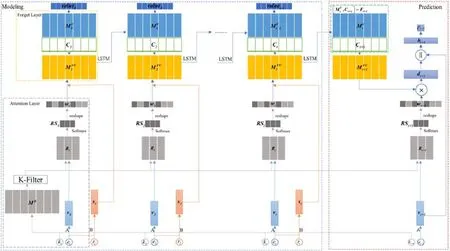
Fig.1 LFKT model图1 LFKT 模型

LFKT 模型分为注意力层(attention layer)、遗忘层(forget layer)、预测层(prediction layer)、学习层(learn layer)以及知识水平输出层(knowledge level output layer):注意力层以习题et以及习题所涵盖的知识点集合kt作为输入,计算习题与各个知识点的知识相关权重;遗忘层根据第3.1 节中提出的影响知识遗忘的4 个因素将学生上一时刻学习结束时知识掌握嵌入矩阵更新为当前时刻学习开始时知识掌握嵌入矩阵,有效地对学生遗忘行为进行建模;预测层根据t+1 时刻开始答题时的预测学生的答题表现;学习层通过LSTM 网络将本次学习开始时的更新为本次学习结束时的,对学生学习行为进行建模;知识水平输出层以学生本次学习结束时的作为输入,输出学生知识水平向量valuet,实时输出学生对于各个知识点的掌握程度.

3.2.1 注意力层

注意力层的作用是计算习题与知识点之间的知识相关权重.注意力层的输入是学生当前练习题目et以及题目所涉及的知识点集合kt.为了将et映射到连续的向量空间,用et乘以习题嵌入矩阵A(dk×|E|),生成一个dk维度的习题嵌入向量vt.其中,矩阵A中每一个dk维列向量为一道习题的嵌入表示.专家标注了每道习题所涵盖的知识点,存放于集合kt中.本文通过知识点过滤器(K-Filter)滤掉不相关知识点,保留习题涵盖知识点.矩阵Rt存储习题涵盖知识点的嵌入向量,其中,矩阵Rt中每一个dk维列向量为习题涵盖的一个知识点的嵌入向量.计算习题嵌入向量vt与涵盖知识点嵌入向量Rt(i)之间的内积,再计算内积的Softmax值并存入向量RSt中.向量RSt表示习题vt与习题涵盖知识点之间的知识相关权重,如公式(1)所示:

|K|维向量wt为习题与全部知识点之间的知识相关权重向量.由于习题涵盖知识点被知识点过滤器滤出,模型需要将习题涵盖知识点的知识相关权重放入到wt对应的位置上.首先,初始化|K|维全零向量wt,即wt←[0,…,0];之后,将RSt每一维的权重放入到wt的相应位置上,即wt[kt[i]]←RSt[i],得到习题与各个知识点的知识相关权重.

3.2.2 遗忘层

遗忘层根据第3.1 节中介绍的影响知识遗忘的因素Ft对上一次学习结束时学生的知识掌握嵌入矩阵进行遗忘处理,得到学生本次学习开始时的知识掌握嵌入矩阵受LSTM中遗忘门与输入门的启发,根据影响知识遗忘的因素Ft更新时,首先要擦除中原有的信息,再写入信息.对于遗忘行为建模来说,擦除过程控制学生知识点掌握程度的衰退,写入过程控制学生知识点掌握程度的更新.遗忘层如图2 所示.

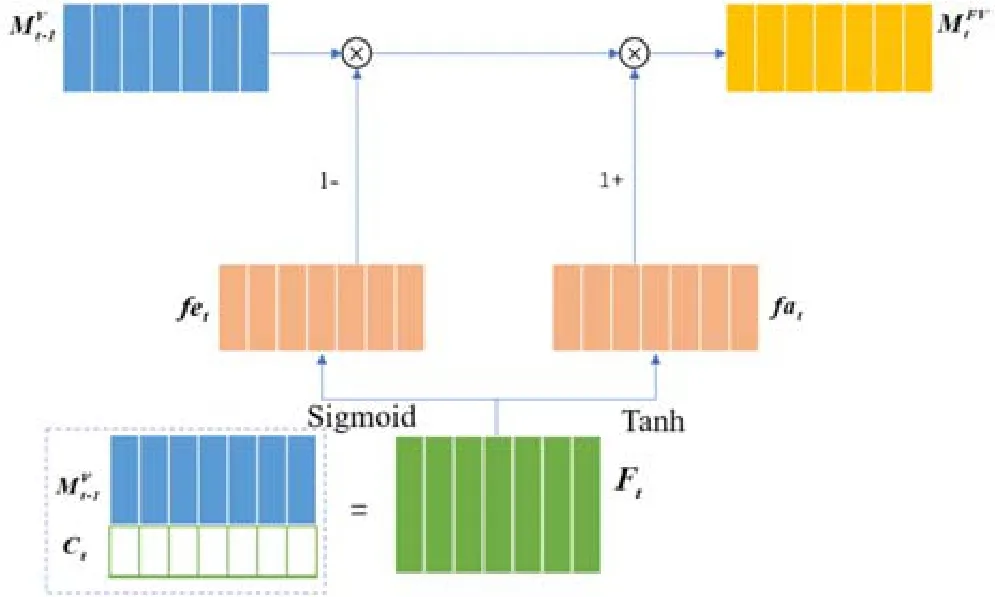
Fig.2 Forget layer图2 遗忘层

利用一个带有Sigmoid激活函数的全连接层将影响学生对知识点i遗忘程度的因素Ft(i)转换为知识点i对应的记忆擦除向量fet(i):

全连接层的权重矩阵FE的形状是(dv+dc)×dv,全连接层的偏置向量bfe为dv维.记忆擦除向量fet(i)是一个维度为dv的列向量,向量中的所有值都是在(0,1)范围之内.利用一个带有Tanh 激活函数的全连接层将影响学生对知识点i遗忘程度的因素Ft(i)转换为知识点i对应的记忆更新向量fat(i):

全连接层的权重矩阵FA的形状是(dv+dc)×dv,全连接层的偏置向量bfa为dv维,记忆更新向量fat(i)是一个维度为dv的列向量.根据记忆擦除向量与记忆更新向量对更新得到

3.2.3 学习层学习层根据学生答题结果追踪学习过程中的知识掌握变化,将学生开始学习时知识掌握嵌入矩阵更新为学生学习结束时知识掌握嵌入矩阵,建模学习行为.元组(et,rt)表示学生在时间t的答题结果,为了将元组(et,rt)映射到连续的向量空间,元组(et,rt)与大小为dv×2|E|的答题结果嵌入矩阵B相乘,得到dv维答题结果嵌入向量st.学习层将答题结果嵌入向量st和习题对应的知识相关权重向量wt作为输入,利用学生在在线教育系统中的练习结果作为学生学习效果的间接反馈,通过LSTM 网络更新学生学习过程中的知识掌握状态,建模学习行为:

3.2.4 预测层

预测层的目的是预测学生在下一个候选习题et+1上的表现.由于学生在两次答题间隔内的遗忘行为会影响其知识掌握状态,预测层根据当前时刻开始答题时的知识掌握嵌入矩阵预测学生正确回答习题et+1的概率.将知识相关权重wt+1与当前时刻开始答题时学生知识掌握嵌入加权求和,得到的向量dt+1为学生对于习题涵盖知识点的加权掌握程度嵌入向量:

学生成功解答习题,不仅与学生对于习题涵盖知识点的综合掌握程度有关,还与习题本身有关,所以将向量dt+1和vt+1连接得到的组合向量[dt+1,vt+1]输入到带有Tanh激活函数的全连接层,输出向量ht+1包含了学生对习题涵盖知识点的综合掌握程度和习题本身的特点.其中,矩阵W1和向量b1分别表示全连接层的权重与偏置:

最后,将向量ht+1输入到一个带有Sigmoid激活函数的全连接层中,得到表示学生答对习题的概率pt+1.其中,矩阵W2和向量b2分别表示全连接层的权重与偏置:

3.2.5 知识水平输出层

在预测层中,每一个时间节点t,公式(7)、公式(8)根据两种输入预测学生在特定习题et上的表现:学生对于该习题涵盖知识点的综合掌握嵌入向量dt和习题嵌入向量vt.因此,如果只是想估计在没有任何习题输入情况下学生对于第i个知识点的掌握情况,可以省略习题嵌入vt,同时,让学生知识掌握嵌入矩阵的第i列作为等式的输入.图3 展示了知识水平输出层的详细过程.具体来说:学习层输出矩阵后,为了估计对于第i个知识点的掌握程度,构造了权重向量βi=(0,…,1,…,0),其中,第i维的值等于1,并用公式(9)提取第i个知识点的知识掌握嵌入向量,之后,使用公式(10)、公式(11)估计知识掌握水平:

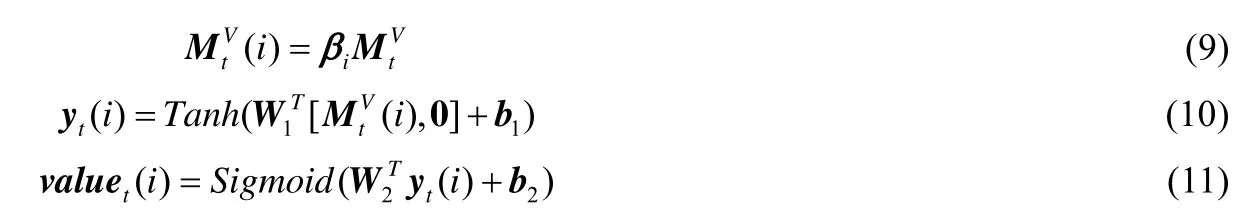
向量0=(0,0,…,0)与习题嵌入vt维度相同,用于补齐向量维度.参数W1,W2,b1,b2与公式(7)和公式(8)中的完全相同.依次计算知识空间中每一个知识的掌握程度,得到学生知识掌握程度向量valuet.

Fig.3 Knowledge level output layer图3 知识水平输出层

3.2.6 模型优化目标

模型需要训练的参数主要是习题嵌入矩阵A、答题结果嵌入矩阵B、神经网络权重与偏置以及知识点矩阵MK.本文通过最小化模型对于学生答题结果的预测值pt和学生答题的真实结果rt之间的交叉熵损失函数来优化各个参数.损失函数如公式(12)所示,本文使用Adam 方法优化参数:

4 实 验

本文在两个真实在线教育数据集上进行实验,通过对比LFKT 模型与其他知识追踪模型的预测性能以及知识追踪表现,证明LFKT 模型的有效性.

4.1 数据集

首先介绍实验所使用的两个真实在线教育数据集.

• ASSISTments2012:该数据集来自于ASSISTments 在线教育平台.本文删除了学习记录数过少(<3)的学生信息,经过预处理后,数据集包含45 675 个学生、266 个知识点以及总计5 818 868 条学习记录.数据集中,user_id 字段表示学生编号,skill_id 字段表示知识点编号,problem_id 字段表示题目编号,correct字段表示学生真实答题结果,start_time 字段表示学生本次开始学习的时间,end_time 字段表示学生本次学习结束的时间;

• slepemapy.cz:该数据集来自于地理在线教育系统.本文同样删除学习记录数过少(<3)的学生信息,经过预处理后,数据集包含87 952 个学生、1 458 个知识点以及总计10 087 305 条学习记录.数据集中,user字段表示学生编号,place_answered 字段表示学生真实答题结果,response_time 字段表示学生学习时间,place_asked 字段表示问题编号.其中,由于该数据集中每个问题仅仅考察一个知识点,因此place_asked 也是知识点编号.

4.2 评测指标

本文使用平均AUC(area under the curve)、平均ACC(accurary)和平均RMSE(root mean squared error)作为评估预测性能的指标.AUC 被定义为ROC 曲线与下坐标轴围成的面积,50%的AUC 值表示随机猜测获得的预测性能,高AUC 值说明模型具有较高的预测性能.ACC 为准确率,即正确预测结果占全部结果的百分比,高ACC值说明模型具有较高的预测性能.RMSE 被定义为预测值与真实值的均方根误差,RMSE 的值越低,说明模型的预测性能越好.对于每一个模型,本文都进行30 次测试,取平均AUC 值、平均ACC 值和平均RMSE 值.

4.3 对比方法与参数设置

为了评估LFKT 模型的性能,本文选择贝叶斯知识追踪[5]、深度知识追踪[8]和动态键-值对记忆网络[9]这3个经典KT 模型作为对比方法.对比方法的参数设置如下.

• BKT[5]:实验设置4 个主要参数:L0表示学生未开始作答时对题目考察知识点的掌握程度,T为学生作答后对知识点掌握程度从不会到会的概率,G为学生没掌握该知识点但是答对题目的概率,S表示学生掌握知识点但是答错题目的概率.BKT 利用以上参数构造一个隐马尔可夫模型,并使用EM 算法求解参数;

• DKT[8]:实验按照Piech 等人[8]的方法设置超参数.循环神经网络GRU 隐藏层的大小为200,批处理大小设置为30,使用Adam 作为优化器,学习率为0.001;

• DKVMN[9]:本文使用Zhang 等人[9]的方法设置超参数.对于ASSISTments2012 数据集,记忆矩阵列数为20,隐藏向量的大小为30.对于slepemapy.cz 数据集,记忆矩阵列数为320,隐藏向量大小为128.批处理大小为30,使用Adam 作为优化器,学习率为0.001.

LFKT 模型:对于ASSISTments2012 数据集,知识嵌入矩阵的列数为266.对于slepemapy.cz 数据集,知识嵌入矩阵的列数为1 458.批处理大小为30,采用Adam 优化器,学习率为0.001.对于知识点嵌入向量的维度dk和学生知识掌握程度嵌入向量的维度dv的超参数设置,本文通过比较模型在测试数据集上的平均AUC值进行选取.为了减少参数数量,本文设d=dk=dv,测试结果见表1.ASSISTments2012 数据集中,当d=dk=dv=32 时,平均AUC 值为0.7513,高于其他超参数设置情况.在slepemapy.cz 数据集中,当d=dk=dv=128 时,平均AUC值为0.8032,高于其他超参数设置.通过对比可知:当d=dk=dv设置过低时,模型的学习能力较低;当d=dk=dv设置过高时候,模型参数过多,容易造成过拟合.因此,对于ASSISTments2012 数据集,设dk=dv=32;对于slepemapy.cz 数据集,设dk=dv=128.

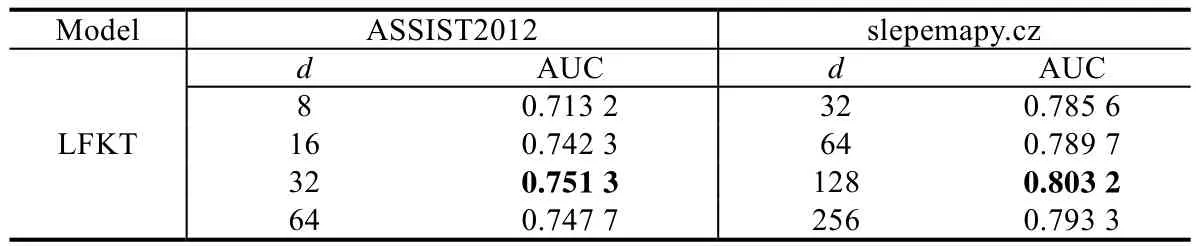
Table 1 AUC results of different hyperparameters表1 不同超参数设置下AUC 值对比实验结果

4.4 学生表现预测结果分析

知识追踪的基本任务之一是,预测学生当前对于下一道候选习题的答题表现.通过对比模型的预测结果与学生的真实答题结果,比较模型的预测性能.本文随机地将数据集中70%的数据作为训练集,另外20%的数据作为测试集,10%的数据作为验证集,用于超参数的调整与早期停止.

表2 给出了LFKT 与3 个对比方法在两个数据集上的平均AUC 值、平均ACC 值和平均RMSE 值的对比结果.LFKT 在两个数据集上的平均AUC 值、平均ACC 值和平均RMSE 值均优于其他3 种对比方法.这一结果表明,LFKT 模型在预测学生未来表现方面性能是优于现有模型的.从实验对比结果可以看出,BKT 在两个数据集上的预测性能最低.这说明BKT 将学生对于某一知识点的潜在知识水平建模为二进制变量是具有局限性的.DKT 利用循环神经网络的潜在向量建模学生整体的知识水平,无法建模学生对于各个知识点的掌握程度,因此DKT 在两个数据集上的预测性能低于DKVMN 和LFKT.DKVMN 与LFKT 都可以建模学生对于各个知识点的掌握程度,但是DKVMN 忽略了学生在学习期间的遗忘行为,默认学生对未复习知识点的掌握程度一直不变,这存在一定的局限性,因此LFKT 的预测性能强于DKVMN.

Table 2 Prediction results of models表2 模型预测性能对比实验结果

除此之外,本文测试了去掉遗忘层后LFKT 模型的预测表现.LFKT 模型去掉遗忘层以后,忽略了学生的遗忘行为,默认学生在学习间隔内,知识水平不会发生任何变化,即.实验结果显示:去掉遗忘层后,LFKT模型的预测性能较没去掉遗忘层时有所下降.这表明学生的遗忘行为对其知识水平有所影响,本文所提出的影响知识遗忘的因素是十分有效的.

4.5 知识追踪结果分析

知识追踪的另一个基本任务是实时输出学生对于各个知识点的掌握程度.本文进行以下实验验证LFKT 模型在知识追踪任务上的有效性.

本文截取了数据集ASSISTments2012 中一位学生在一段时间内的学习记录,并分别使用LFKT 模型和DKVMN 模型追踪学生对于5 个知识点掌握程度的变化,如图4 和图5 所示.图中横轴表示学生的学习历史,元组(kt,rt)中kt表示学生学习的知识点,rt表示学生作答情况.纵轴表示模型追踪的5 个知识点.

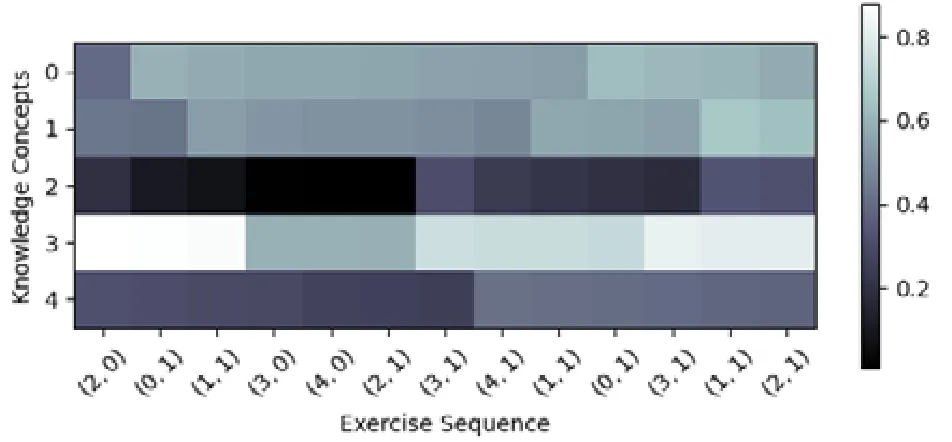
Fig.4 Knowledge level output result of LFKT in ASSISTments2012图4 ASSISTments2012 数据集LFKT 知识水平输出结果

Fig.5 Knowledge level output result of DKVMN in ASSISTments 2012图5 ASSISTments 2012 数据集DKVMN 知识水平输出结果

实验结果显示:在第2 时刻,学生对知识点0 答题正确后,DKVMN 和LFKT 模型对学生知识点0 掌握程度的追踪结果都有所提高(输出值增加);在第4 时刻,学生对知识点3 对应习题答题错误后,DKVMN 模型和LFKT模型对学生知识点3 的掌握程度的追踪结果都有所下降.以上结果说明:DKVMN 模型和LFKT 模型在获得学生作答结果以后,都会根据学生的作答结果更新对应知识点的掌握程度,以此建模学生的学习过程.图4 和图5中,学生第2 时刻学生学习知识点0 到第10 时刻第2 次学习知识点0 期间,DKVMN 模型并没有更新学生对于知识点0 的掌握程度,而LFKT 模型显示学生对于知识点0 的掌握程度一直在下降.由此可以看出:DKVMN 模型没有考虑学习者在学习期间的遗忘行为,而LFKT 模型考虑了学习者在学习期间的遗忘行为.以上结果表明:LFKT 模型与DKVMN 模型都可以建模学生的学习行为,DKVMN 模型无法建模学生的遗忘行为,而LFKT 模型可以建模学生的遗忘行为,并实时追踪学生对于各个知识点的掌握程度.

本文在slepemapy.cz 测试数据集中随机抽取3 名学生在一段时间内的学习记录,并分别使用LFKT 模型与DKVMN 模型输出其对5 个知识点的掌握程度.3 名学生的部分答题序列如下.

•Ha=[(1,1),(2,1),(3,1),(4,0),(5,0),(6,0),(1,0),(2,1),(3,1),(4,0),(5,1),(6,1)];

•Hb=[(6,1),(5,1),(4,1),(3,1),(2,1),(1,1),(2,1),(3,1),(4,1),(5,1),(6,1),(1,1)];

•Hc=[(1,1),(2,1),(3,1),(4,0),(5,1),(6,1),(1,1),(2,1),(3,0),(4,1),(5,0),(6,0)].

序列中的每一项(kt,rt)表示学生作答的结果,其中,kt表示学生当前作答习题所涵盖的知识点,rt表示学生的答题结果,结果为0 表示答错,结果为1 表示答对.

Fig.6 Knowledge level output result in slepemapy.cz图6 slepemapy.cz 数据集知识水平输出结果

LFKT 模型与DKVMN 模型对学生各个知识点掌握程度的追踪情况如图6 所示,其中:实线表示LFKT 模型对于学生知识点掌握程度的追踪情况,虚线表示DKVMN 模型对于学生知识点掌握程度的追踪情况.以图6(c)为例,学生a在第3 时刻正确回答涵盖知识点3 的习题,LFKT 与DKVMN 输出的知识点掌握程度值均在第3时刻后开始增加.该结果说明,LFKT 与DKVMN 均可以根据学生的答题结果建模学生学习行为.图6(a)中,学生a在第8 时刻后一直没有复习知识点1,在第8 时刻以后,DKVMN 输出的对应知识点掌握程度值变化很小,但LFKT 输出值变化较大,呈持续下降趋势.该结果说明:LFKT 模型可以建模学生的遗忘行为,追踪到学生由于遗忘而产生的知识掌握程度变化;但DKVMN 忽略了学生的遗忘行为,无法追踪学生由遗忘产生的知识水平变化.本文汇总了ASSISTments2012 测试集中所有学生答对一道习题后的答题序列,记录LFKT 输出的知识点掌握程度,并记录学生下一次作答涉及该知识点习题时LFKT 输出的知识点掌握程度,求解下一次答题时LFKT输出的知识点掌握程度距上一次答题结束时LFKT 输出的知识点掌握程度的衰减比例,即valuet+1(i)/valuet(i).图7 显示了学生平均知识掌握程度衰减比例与重复学习知识点次数与时间间隔之间的关系.纵轴表示重复学习知识点次数,单位为“次”;横轴表示距离上次学习知识点的间隔时间,单位为“分钟”.数据集中的间隔时间从0分到几天不等,因此本文通过log2(RT)的方法降低横轴的长度.由结果可知,LFKT 模型再现了学生复杂的遗忘行为,即:在相同间隔时间的情况下,重复学习次数越多,由于遗忘引起的知识点掌握程度的衰减比例越低;在相同重复学习次数的情况下,间隔时间越长,由于遗忘引起的知识点掌握程度衰减比例越大.由此可以看出:LFKT可以根据影响知识遗忘的因素挖掘遗忘规律,建模遗忘行为,准确计算出由于遗忘引起的知识掌握程度变化.

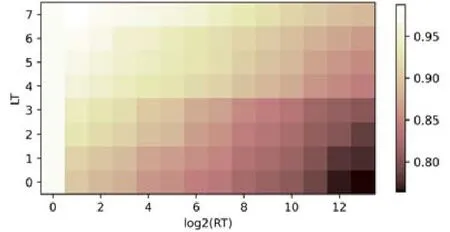
Fig.7 Quantized distribution map of knowledge level decline ratio of LFKT against repeated time interval and repeated learn times图7 LFKT 知识水平输出衰减比例与间隔时间和重复次数的量化分布图

5 总结与未来工作

本文重点考虑了学生遗忘行为对其知识掌握程度的影响,提出了融合学习与遗忘的深度知识追踪模型LFKT.实验表明,LFKT 在预测学生答题表现方面优于传统知识追踪模型BKT,DKT 和DKVMN.LFKT 在追踪学生知识水平变化时,不但可以根据学生答题情况追踪学生学习过程中的知识水平变化,还可以体现由复杂知识遗忘因素导致的学生遗忘行为,并实时追踪由于学生遗忘造成的知识水平变化过程.

在未来的研究中,我们将针对以下方面进行探索.

(1)知识点之间的关系特征对知识追踪的影响.知识点之间存在先验、后验、包含等关系,需要明确知识点之间的关系特征,进而准确推测学生对于各个知识点的掌握程度;

(2)本文所采用数据集中习题涉及的知识点相对较少,比较容易根据学生的答题结果追踪学生对于习题考察知识点的掌握程度.对于覆盖知识点数量较高的习题,如综合性习题,会导致知识点掌握程度的不确定性.知识点高覆盖率下的知识追踪,也是我们下一步的研究工作.