基于车辆-轨道耦合动力学的400 km/h高速铁路线路平面参数设计研究

翟婉明 姚 力 孙 立 王开云 朱胜阳

(1.西南交通大学牵引动力国家重点实验室, 成都 610031；2.中铁二院工程集团有限责任公司， 成都 610031；3.中铁第四勘察设计院集团有限公司， 武汉 430063)

1 研究背景

强化前沿关键科技研发，深入400 km/h高速铁路技术研究，是新时代国家建设“交通强国”的重大需要[1]，也是高速铁路发展的重要趋势和现阶段面临的重大课题[2-5]。在更高的速度等级下，车辆-轨道系统动力相互作用加剧，列车的行车安全性、运行平稳性及乘坐舒适度受轨道结构参数的影响更加突出[6]，尤其在曲线线路这一铁路薄弱环节上，线路平面参数即超高、曲线半径和缓和曲线长度等的设置将直接影响行车的动力学性能[7-8]，既有350 km/h及以下线路平面参数设计规范的适应性势必会受到影响。因此针对400 km/h高速铁路，分析既有规范的适应能力，并开展曲线设置参数的合理匹配研究，对推动高速铁路向更高速度发展具有重大意义。

目前，针对高速铁路线路平面参数已有不少研究。高速列车与线路的动力相互作用问题，并非机车车辆或轨道单一系统的孤立问题，对此，翟婉明率先提出车辆-轨道耦合动力学理论，并成功应用于一系列与铁路发展密切相关的关键动力学问题的研究之中[9-11]。王开云等人针对提速和高速铁路，开展了曲线线路轮轨动态相互作用性能匹配研究，制定了主要动力性能指标的评价标准。徐鹏等人[12]通过建立列车-轨道动力学分析模型，确定了既有试验线开行速度385 km/h时的曲线超高调整方案。梁晨等人[13]通过理论计算与车辆动力学模型仿真检算相结合，分析最小曲线半径值的控制要素及取值，结果表明：400 km/h与350 km/h及以下时速匹配时，最小曲线半径取值仅由设计时速控制，而与匹配速差无关，推荐困难条件下400 km/h的最小半径值为7 500 m。刘磊等人[14]通过理论分析，对400 km/h高速铁路的最大超高、欠超高以及单列车与高低速共线运行时的最小曲线半径进行研究，并取曲线设置超高值为175 mm，对车辆通过不同曲线半径地段进行仿真分析，结果表明：400 km/h高速铁路的最大设置超高、欠过超高之和等超高参数可沿用既有350 km/h的规范取值。时瑾等人[15]从安全性、舒适性角度分析了不同时速下的最小曲线半径取值以及小半径值对应的最佳超高值，认为适当欠超高更有利于优化行车性能。

由此可见，目前大多数高速铁路线路平面参数设计的研究是针对350 km/h及以下速度[16-18]的。对400 km/h线路平面参数的研究主要集中在基于静力学和车辆动力学理念，分析曲线半径最小值、最大超高值等关键参数的取值上，对曲线半径超高匹配问题未深入研究，且动力学分析未考虑曲线通过时随机不平顺激励对车辆-轨道系统动态特性的影响，与实际情况差距较大。有学者采用商业软件开展曲线半径、超高与时速的匹配性研究，但研究过程中多采用固定超高值或固定曲线半径值的单一变量分析方法，忽略了不同半径曲线与不同超高匹配时的特殊性，具有一定的局限性。而为充分研究400 km/h条件下曲线参数的匹配关系，应细致考虑各参数对车辆-轨道系统动力学特性的影响。因此针对400 km/h高速铁路线路平面参数尚待开展深入系统的理论研究。

鉴于此，本文基于车辆-轨道空间耦合动力学，建立可反映400 km/h行车条件及曲线线路状态下轮轨动态相互作用关系的动力学仿真模型。以随机轨道不平顺作为模型激励，计算列车动态通过不同曲线半径和超高平纵断面时的动力学性能，以开展既有线路平面参数设计规范的适应性分析与400 km/h线路平面参数设计研究，为400 km/h高速铁路基础设施设计，提供理论依据和科学参考。

2 动力学模型及研究技术路线

2.1 动力学研究模型

在更高时速条件下，列车曲线通过时的轮轨相互作用问题突出，动力学研究不能简单从车辆或线路本身进行考察，而应将车辆与线路视为整体系统进行研究。为此，本文依据车辆-轨道耦合动力学理论[19]，建立了高速铁路车辆-轨道空间耦合动力学仿真模型。

高速铁路车辆-轨道空间耦合动力学分析模型如图1所示。车辆采用整车多刚体模型，考虑车体、前后构架及轮对的沉浮、横移、侧滚、点头、摇头，共35个自由度。轨道以无砟轨道为对象，采用钢轨-轨道板-底座板-路基结构组成的弹簧阻尼振动模型进行模拟。其中，钢轨视为连续弹性离散点支承的Euler梁模型，轨道板和底座板横向视为刚体运动，垂向视为弹性地基上四边自由的弹性薄板模型。在轮轨关系中，轮轨法向力由赫兹非线性弹性接触理论确定，轮轨蠕滑力依据kalker线性蠕滑理论进行计算，并按沈氏蠕滑理论进行非线性修正。车辆-轨道空间耦合动力学模型的振动方程和数值积分方法详见文献[19]。

图1 车辆-轨道空间耦合动力学模型图

为实现对车辆通过完整曲线路段的模拟，曲线通过工况仿真采用由直线段、缓和曲线段和圆曲线段构成的曲线线路尺寸。轨道不平顺是车辆运行中系统振动的主要根源，仿真过程充分考虑随机不平顺的激扰影响，采用2～200 m波长范围的中国高速谱拟合不平顺样本作为轮轨激励，如图2所示。

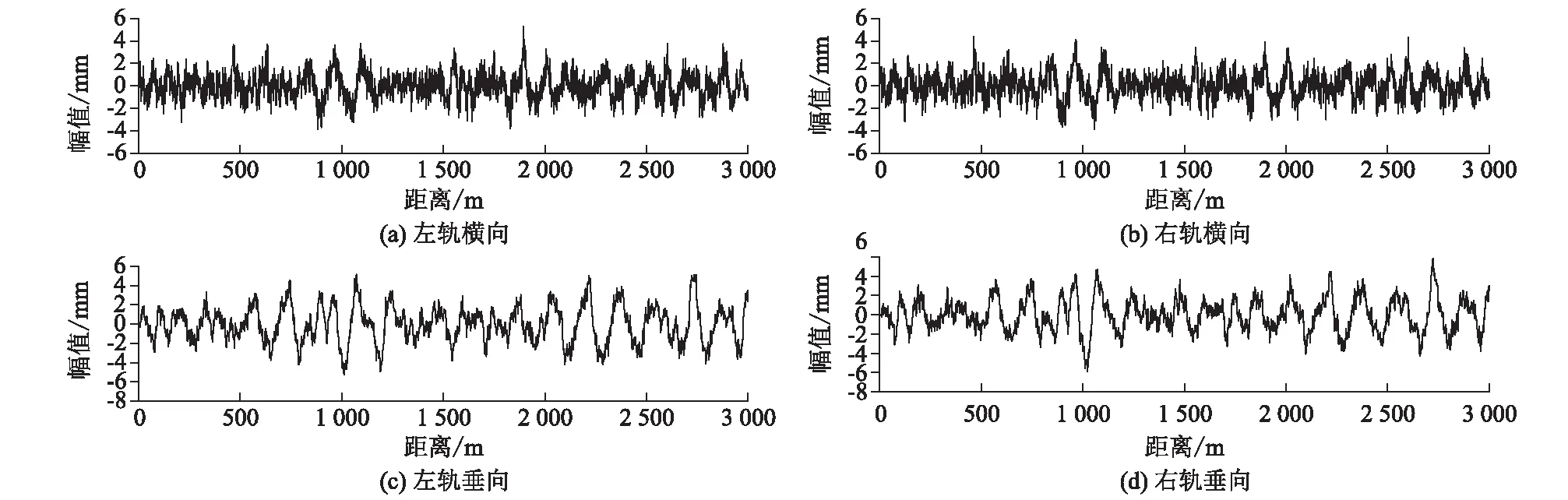
图2 轨道随机几何不平顺图

2.2 适应性分析技术路线

TB/T 10621-2014《高速铁路设计规范》[20]给出了350 km/h及以下线路平面参数设计的合理参数值，如表1所示。当采用表中数值间的曲线半径时，相应的缓和曲线长度采用线性内插得到。为分析规范对400 km/h曲线线路的适应性，本文取规范给定的最高设计时速(350 km/h)对应的曲线参数，进行不同时速条件下的仿真分析。技术线路为:(1)由超高时变率定义，理论计算表1所列350 km/h曲线线路的超高值；(2)仿真计算350 km/h、400 km/h条件下各曲线线路的各项动力学特性指标；(3)结合指标规定限值，分析时速变化对动力学性能的影响规律及线路参数对400 km/h的适应性。

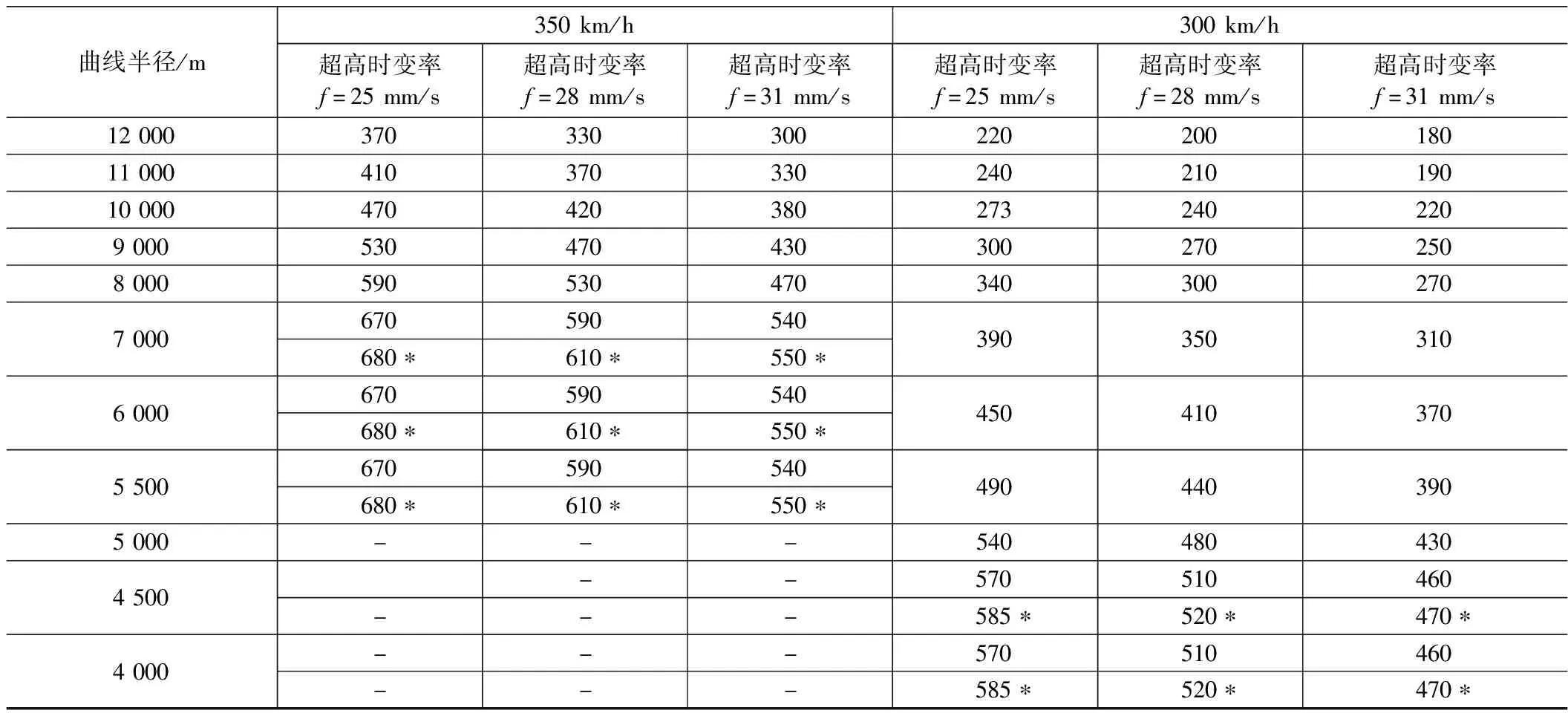
表1 350 km/h及以下曲线线路缓和曲线长度表

2.3 设计分析技术路线

在400 km/h线路平面参数动力学设计分析中，结合线路关键参数特点，充分考虑400 km/h条件下可能的曲线线路，全面考察轨道随机不平顺激扰条件下车辆曲线通过的安全性、平稳性以及系统动态相互作用性能等动力学评价指标，研究曲线半径、超高及超高时变率等关键线路参数对系统动态相互作用关系的影响规律，综合分析得出400 km/h曲线线路关键参数的推荐值。

设计分析技术线路如图3所示，其中400 km/h条件下的合理曲线半径范围由理论计算和动力学检算得到。仿真提取响应包括车体心盘处的垂向与横向加速度、轮轨垂向力与横向力，并进一步求解车辆运行安全性评价指标(脱轨系数、轮重减载率)、平稳性评价指标(垂向、横向Sperling指标)以及车辆轨道动态作用评价指标(轮轴横向力)，各项性能指标限值规定如表2所示[21]。

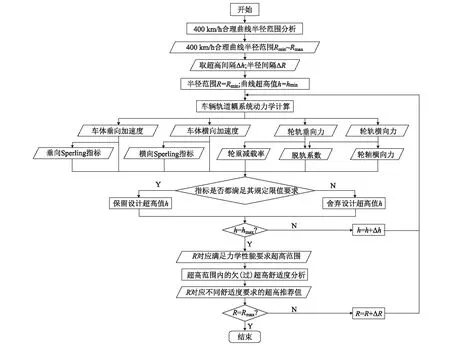
图3 400 km/h线路平面参数设计动力学分析技术线路图

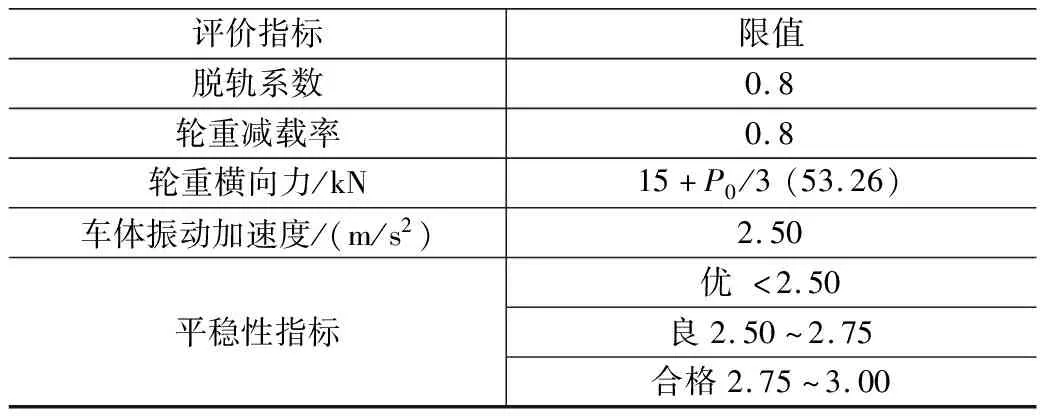
表2 评价指标及限值表

3 高速铁路线路平纵断面参数分析

3.1 最大设置超高

铁路线路实设最大超高允许值须满足稳定性要求，保证行车安全，避免车辆通过时发生向内倾覆。为此最大超高允许值的取值[22]:

(1)

式中：S1——两轨头中心距(mm)；

H——车体重心至轨顶面高(mm)；

N——稳定系数，当n小于1时车辆丧失稳定而倾覆，根据国内外铁路运营经验，n值不应小于3。

标准轨距S1为 1 500 mm，复兴号动车车体重心至轨顶面高H为 1 670 mm，计算得最大超高值为225 mm。此外，曲线最大实设超高还应考虑列车在曲线上停车时，乘客处于倾斜车体中的舒适度反应。综合考虑各种因素，高速铁路实设超高最大允许值为170～180 mm。因此，建议400 km/h最大设计超高为175 mm。

3.2 欠(过)超高允许值

若通过设置外轨超高产生的向心加速度正好平衡列车以速度V做曲线运动的离心加速度，则列车处于最理想的运动状态。此时的实设超高为速度V对应的均衡超高。根据平衡关系，均衡超高的计算式为:

(2)

对于标准轨距:

(3)

式中：S1——两轨头中心距；

G——重力加速度，g=9.8 m/s2；

R——曲线半径(m)；

V——车辆速度(km/h)。

设计超高h大于或小于均衡超高值时，均存在未平衡超高度△h，过超高hg和欠超高hq的计算式为:

(4)

(5)

未平衡超高受乘客舒适度要求限制。根据平衡原理，未平衡超高Δh与车体未被平衡加速度α关系为:

(6)

对于标准轨距:

Δh=153α

(7)

我国在制定高速铁路技术标准[23]时，分别按α=0.26 m/s2、0.39 m/s2、0.59 m/s2选定了三级欠/过超高最大允许值，如表3所示。

表3 高速铁路欠/过超高最大允许值表(mm)

3.3 最大曲线半径

最大曲线半径与线路铺设、养护、维修的要求精度有关，曲率过小时，维修难度加大，曲线平顺性不易保证。综合国内外的工程实践经验和科研成果，我国速度300～350 km/h高速铁路的最大圆曲线半径取值为 12 000 m[23]。考虑技术经济条件，400 km/h线路可沿用350 km/h的最大曲线半径值。

3.4 最小曲线半径

最小曲线半径应满足乘客的舒适度要求，保证曲线通过时，欠超高hq不超过其允许值hqy。文献[13]的研究结果表明，400 km/h线路最小曲线半径主要由设计时速控制，而与匹配速差无关，因此400 km/h线路的最小曲线半径按单一高速列车条件计算:

(8)

取最大设置超高hmax=175 mm，欠超高允许值hqy=90 mm，则400 km/h最小曲线半径理论分析值Rmin=7 124 m。

4 既有曲线参数适应性分析

根据缓和曲线长度、曲线半径和超高时变率的关系，可得表1所列33段曲线线路的主要参数如表4所示，其中缓和曲线长度按10 mm进整。对33段线路依次进行350 km/h和400 km/h的车辆曲线通过仿真分析，第33段线路工况对应的车体右侧前心盘处车体加速度和一位轮对处轮轨力在不同时速下的时程响应分别如图4和图5所示。图中左、右侧分别表示曲线线路外侧和内侧。

表4 既有规范推荐设计速度350 km/h的曲线参数表

图4 通过第33段曲线时车体心盘处加速度响应图

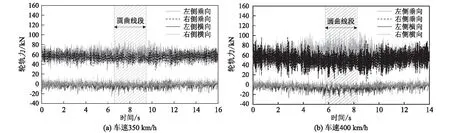
图5 通过第33段曲线时轮轨力响应图

从图4、图5可以看出，车辆通过曲线时，车体横向加速度最大幅值明显大于车体垂向加速度最大幅值，前者约为后者的2～3倍，两者最大振幅出现的位置也不相同。对于同一曲线线路，当车辆速度从350 km/h提高到400 km/h时，车体垂向加速度和横向加速度均出现不同程度的振幅增大。曲线通过时，轮轨横向力在0附近变化，垂向力在静轮重(58.56 kN)附近变化。由于既有标准均按欠超高设计，因此车辆通过曲线时外侧钢轨的轮轨作用力幅值大于内侧。各曲线工况下，速度提升时轮轨力幅值增大明显。以第33段曲线工况为例，速度350 km/h与速度400 km/h对应的轮轨横向力最大幅值分别为25.9 kN、29.4 kN，增幅为13.5%；轮轨垂向力最大幅值分别为89.8 kN、107.5 kN，增幅为19.7%。

由此可见，速度提高后系统动力相互作用更加剧烈。因此，对于设计速度400 km/h的线路，采用既有针对设计速度350 km/h及以下的线路平面参数设计规范，存在动力学性能指标超限风险，需进一步分析400 km/h车辆通过既有规范给定线路的动力学性能。

在33组线路工况下，以350 km/h通过各段曲线的车辆运行Sperling平稳性指标和车辆-轨道动态作用评价指标如表5所示，以400 km/h通过各段曲线的各项动力学指标如表6、表7所示。各表中，超限工况以加粗字体标出，Sperling指标分别以白色、浅灰色和深灰色3种不同灰度背景表示优(< 2.5)、良(2.5～2.75)和合格(2.75～3.0)等级。

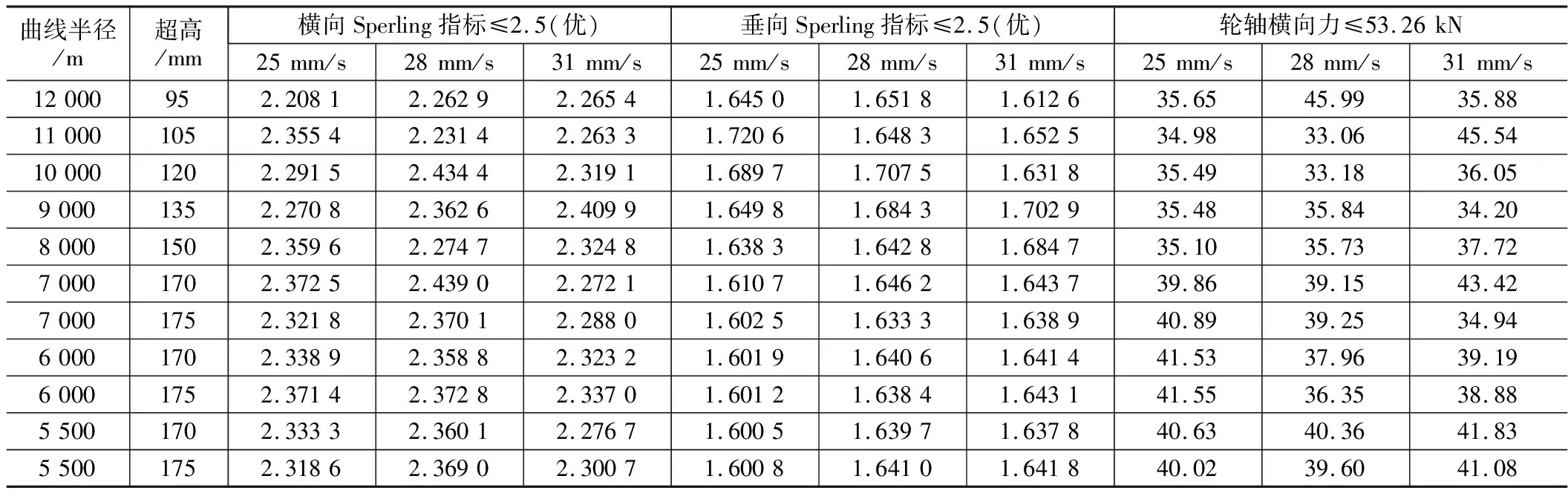
表5 以350 km/h通过各段曲线的车辆运行Sperling平稳性指标和车辆-轨道动态作用评价指标表

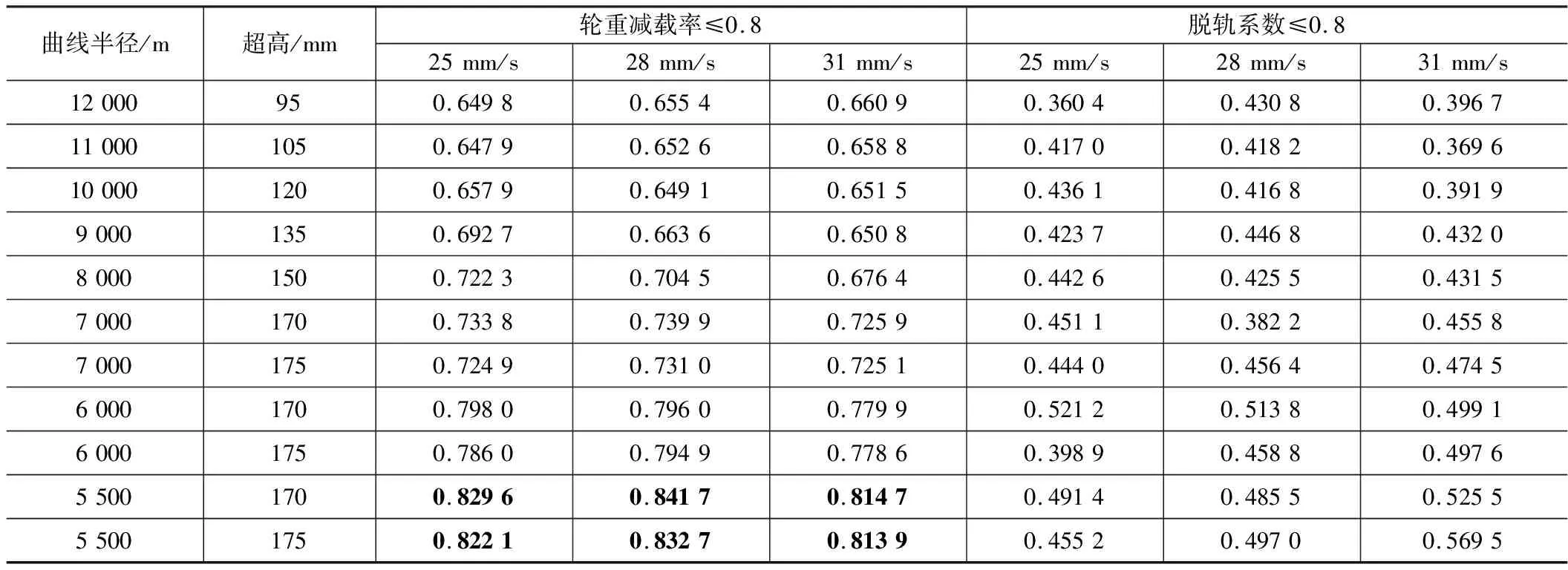
表7 以400 km/h通过各段曲线的车辆运行安全性指标表

从表5～表7可以看出：(1)350 km/h条件下各线路工况均满足限值要求，且Sperling指标均达到“优”等级，表明规范对350 km/h线路的适应性良好；(2)400 km/h条件下，车体垂向与横向加速度、垂向与横向Sperling指标均未超限，垂向Sperling指标均为“优”等级，横向Sperling指标较350 km/h均有所增大，且大多工况处于“良”等级，少数工况处于“优”或“合格”等级；(3)400 km/h条件下，小半径曲线工况对应的安全性指标偏于“危险”，半径 6 000 m及以下工况的轮重减载率均大于0.75，且半径 5 500 m对应各组工况的轮重减载率均超限，半径 5 500 m时轮轴横向力有3组超限工况；(4)在相同半径、超高匹配条件下，3种常用超高时变率对应的动力学指标相差小，且大小次序随机，可见常用超高时变率的选择对动力学性能指标的影响不明显。

综合各项指标结果，并考虑预留一定的安全裕量，对于400 km/h的线路，既有标准在 5 500～7 000 m半径范围内不再适用，在>7000 m半径范围内具有一定的适应能力。

5 400 km/h超高设计建议值分析

5.1 曲线半径合理设置范围

从动力学角度对公式(8)计算得到的400 km/h线路最小半径值(Rmin=7 124 m)进行检算分析。检算中，半径分析范围为 5 500～7 500 m，间隔100 m；超高分析范围为0～300 mm，间隔10 mm；因超高时变率变化对动力学性能的影响不明显，故均取25 mm/s。为综合比较参数变化对各项指标的影响规律，对各仿真工况计算结果按指标最大值比指标限值进行归一化处理，部分数据结果如图6、图7所示。图中平稳性指标展示了按“优”、“良”等级的归一化结果。

图6 半径5 500 m指标归一化值变化曲线图

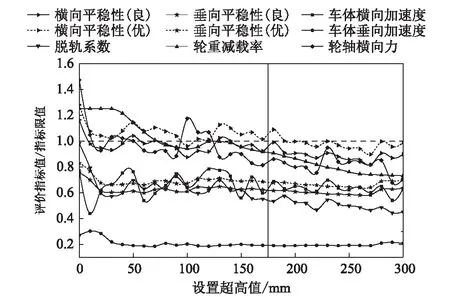
图7 半径7 000 m指标归一化值变化曲线图

从图6、图7可以看出，曲线半径与超高匹配关系变化时，垂向平稳性指标、车体垂向加速度和车体横向加速度基本满足限值要求，脱轨系数、轮重减载率、轮轴横向力以及横向平稳性指标较易发生超限。半径较小时(如R=5 500 m)，在0～hmax(hmax=175 mm)超高范围内动力学性能无法满足限值要求。当半径增大到 6 000 m，在0～175 mm范围内开始存在满足动力学性能要求的区间。区间超高值上限为175 mm，以半径 7 000 m为例，当超高值大于175 mm时，仍可满足动力学性能指标要求，这是因为半径 7 000 m对应的均衡超高为270 mm，稍大于175 mm的超高值更接近与均衡状态，因此必要时适当放宽最大超高值限值是可取的。

区间下限由性能指标综合评定，不同半径对应的未超限的区间下限值如图8所示。

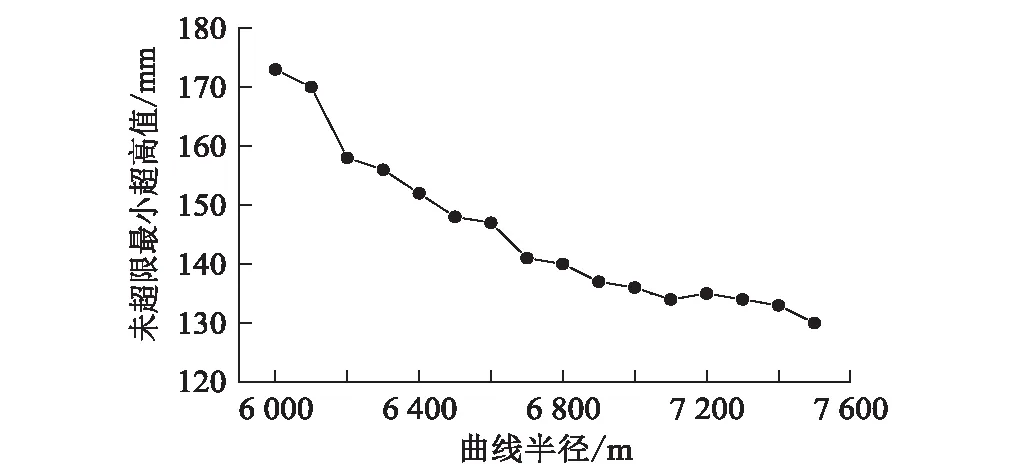
图8 满足限值区间下界值随半径增大变化规律图

从图8可以看出，随着半径的增大，未超限区间的下限值减小，半径 6 000 m、7 500 m对应的未超限最小超高值分别为173 mm、130 mm，表明当半径值大于 6 000 m时开始存在满足动力学要求的超高区间。随着半径的增大，满足限值的超高区间也扩大，半径 7 000 m和 7 500 m对应的区间分别为136～175 mm、130～175 mm。故式(8)计算得到的最小半径值(Rmin=7124 m)在一定超高范围内可满足动力学指标要求，且具有一定的安全裕量。对该值以500 m进整，建议400 km/h高速铁路最小半径取7 500 m。

5.2 线路平面参数设置建议值

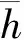
从图9可以看出，当半径为 7 500 m时，均衡超高为251 mm，按“优秀”、“良好”、“一般”3种等级确定的最小超高值分别为211 mm、191 mm和161 mm，在0～hmax的超高范围内，欠/过超高舒适度最佳能达到“一般”等级，其对应超高范围为160～175 mm；当半径增大至 8 500 m时，舒适度最佳可满足“良好”等级；当半径增大至 9 000 m时，0～hmax内可设置3种舒适度要求的超高值；当半径为 12 000 m时，3种等级对应的最小超高值分别为117 mm、97 mm和67 mm，此时均衡超高值为157 mm，在0～hmax超高范围内存在过超高设计。曲线半径通常按欠超高状态进行设计，而上述结果表明，当线路曲线半径较大时，适当采用过超高形式设计也是合理的。

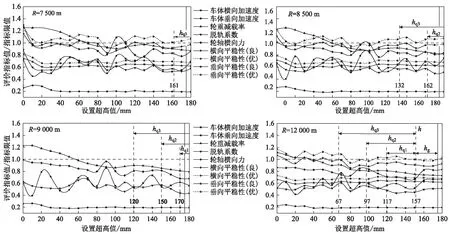
图9 不同曲线半径时动力学性能随超高变化曲线图

对动力学性能综合分析可得，当半径为 7 500 m时，在未超限超高区间基础上留有安全裕量的安全超高范围为140～175 mm，在该范围内横向平稳性指标均满足“良好”等级，接近“优秀”等级，表明既有欠/过超高要求的超高范围(160～175 mm)具有20 mm的安全裕量；当半径为 12 000 m时，安全超高范围为55～175 mm，在该范围内横向平稳性指标均可达“良好”等级，部分达到“优秀”等级，表明既有欠/过超高要求的超高范围(65～175 mm)具有10 mm的安全裕量。由此可见，既有标准对不同曲线半径的欠/过超高要求具有一定的安全裕量，欠/过超高要求相比动力学性能指标更为严格。

综合动力学性能分析与欠/过超高舒适度分析，得出满足动力学性能要求条件下，各曲线半径对应不同舒适度条件的超高推荐值如表8所示，对应缓和曲线长度推荐值如表9所示。进一步评估推荐超高值安全裕量并汇总，如表10所示。其中安全最小超高值为动力学性能指标所确定安全超高区间的区间下限值。

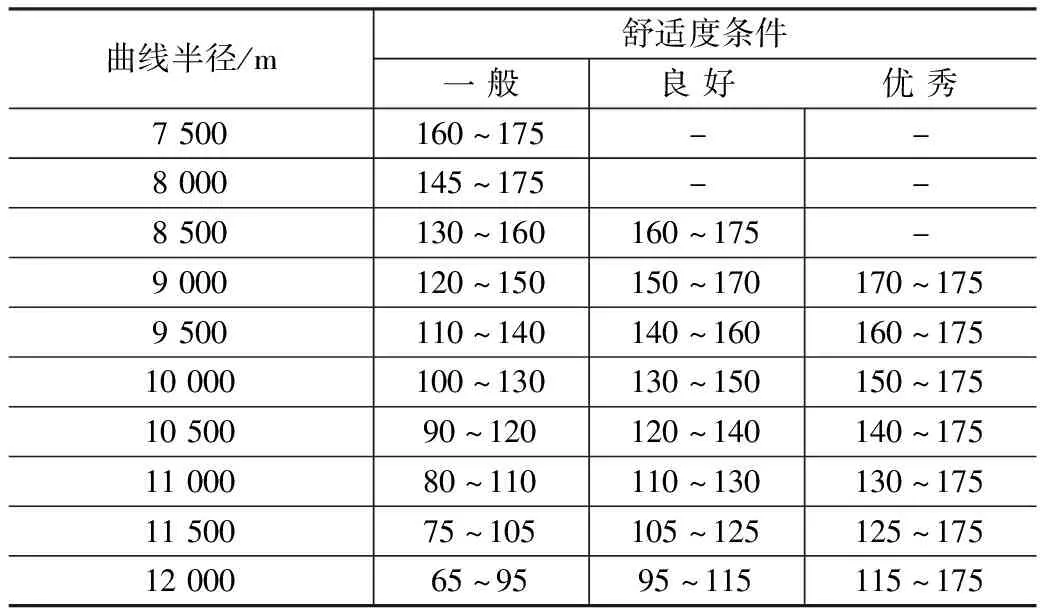
表8 400 km/h曲线超高设置推荐值表(mm)

表9 400 km/h曲线线路缓和曲线长度推荐值(m)

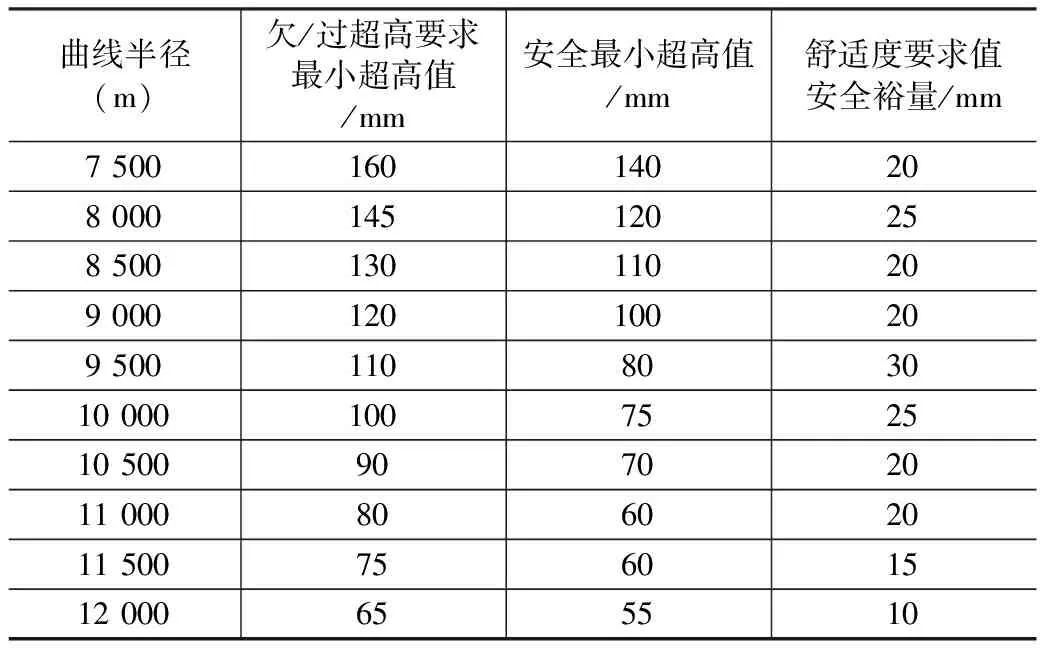
表10 既有欠/过超高舒适度要求最小超高的安全裕量表

6 结论

本文建立了高速车辆-轨道空间耦合动力学模型，围绕400 km/h高速铁路线路平面参数设计，系统性地开展了既有规范适应性分析与线路平面参数合理匹配研究，为我国400 km/h等级高速铁路设计提供重要理论支撑，主要研究结论如下:

(1)列车速度从350 km/h提高到400 km/h，车辆-轨道系统动力相互作用加剧，既有规范适应性发生变化。当曲线半径在 7 000 m及以下时，会出现动力学指标超限或安全裕量小的现象，表明既有规范不再适应于400 km/h的线路设计，但对 7 000 m以上的曲线半径仍具备一定的适应能力。

(2)对于400 km/h高速铁路，当曲线半径大于 6 000 m时，便存在满足动力学指标限值要求的超高区间，且半径越大区间范围越大。考虑同时满足动力学指标和欠/过超高限值要求，并留有一定的安全裕量，本文建议400 km/h高速铁路曲线半径不应小于 7 500 m。

(3)相比于既有欠/过超高设计要求，综合考虑车轨系统动力学性能指标来设计曲线超高具有更宽的合理设置范围。本文提出了400 km/h条件下线路平面设计参数推荐值，并评估了其安全裕量，可供不同线路条件和工程要求选用。