滚筒洗衣机负载不平衡识别算法可靠性设计与实现

谢建军 郑明星 戴浩乾 施清清 王晓楠

（珠海格力电器股份有限公司 珠海 519070）

引言

目前，滚筒洗衣机逐渐的成为日常生活中不可缺少的家用洗涤电器，随着用户的使用频次增加，洗涤的衣物种类增多。对滚筒洗衣机的各方面的性能提出了更高的要求。最为突出的问题为滚筒洗衣机脱水过程中发生的撞筒移位和部分衣物种类不脱水的现象发生，该售后反馈数量在滚筒洗衣机问题反馈中占比较大。

一般的针对滚筒洗衣机不平衡量的检测在静态过程中进行，在洗衣机稳定状态下进行不平衡状态的识别。该方案针对大多数情况稳定性较好，满足正常环境的使用需求。在实际使用过程中，为满足不同用户在不同环境使用滚筒洗衣机的需求，提升产品可靠性，需要提升不平衡量识别与控制的可靠性。本文针对不同的使用场景在实验室进行情景模拟分析，依据实验结果，提出优化不平衡的识别与控制方案。提升滚筒洗衣机的脱水性能的同时提供一种可靠可执行的系统性解决思路。

1 不平衡控制方法分析

在弹簧——阻尼模型的滚筒洗衣机中，衣物状态分布不均匀时，将产生不平衡的运动过程，该简易模型如图1所示。

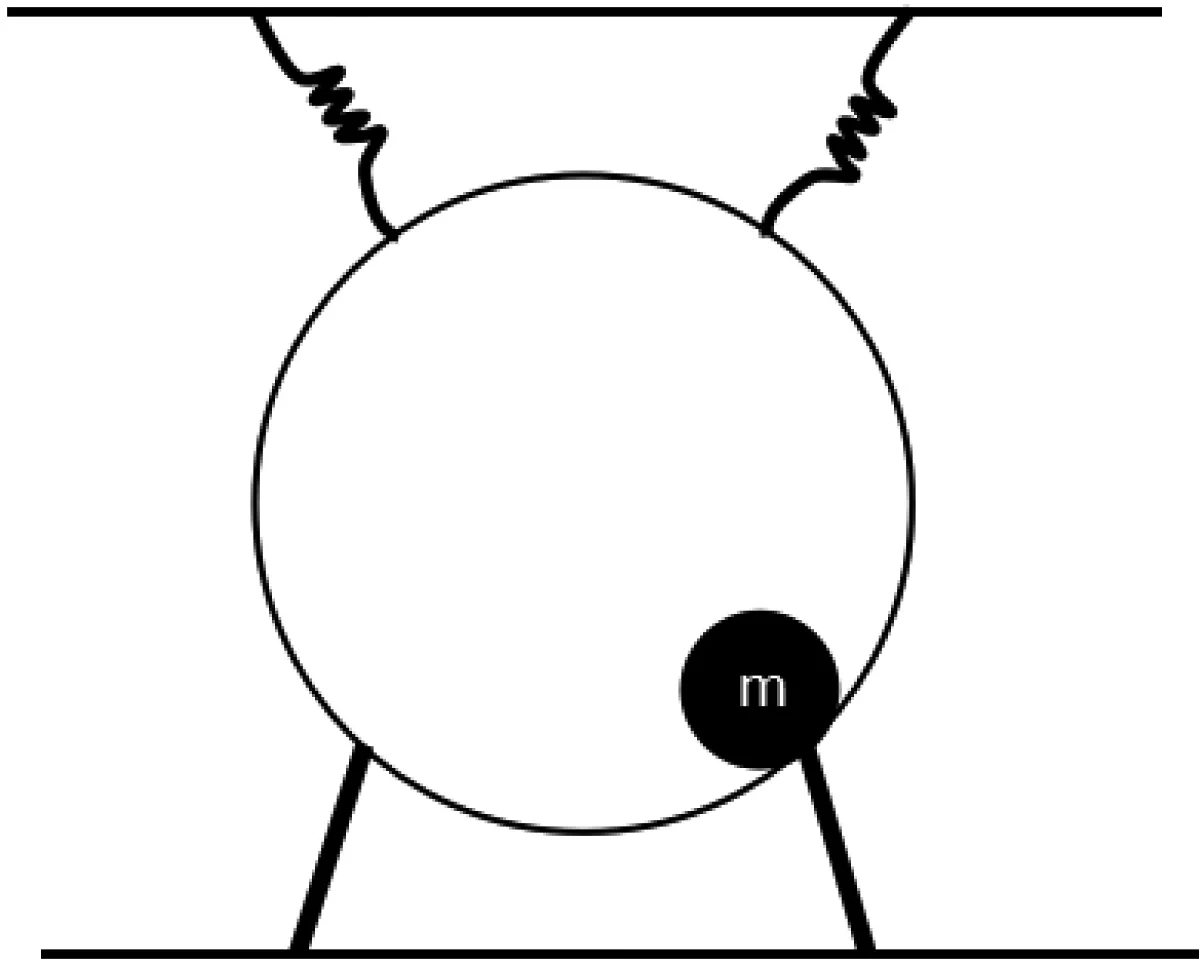
图1 不平衡状态运行简易模型

在上述模型中，m为模拟衣物不平衡量，电机为BLDC电机，当m在筒内旋转时，此时洗衣机状态为不平衡的状态，该状态将反馈在电机参数中，如电压、电流、功率、转速、转矩等各项参数，均存在不同变化趋势。通过辨识各参数的变化率，可以识别出此时系统内部的衣物状态的相对不平衡量的相对值。

根据动力学原理可列出机械运动方程，如下：

式中：

te—电磁转矩；

tL—负载转矩。

在转速Ωr恒定时，系统转动惯量J，阻尼系数RΩ在同一工况下均可作为常量，由上面机械运动方程可知，对系统转速的控制需要通过控制动转矩（te-tL）来实现，若负载状态发生变化，产生不平衡状态，将系统稳定在某一转速时，电磁转矩te将通过调整自身输出，使得转速达到设定的目标转速。此时电磁转矩的调整过程中的变化量可作为负载状态不平衡量A的相对标示值，公式如下：

式中：

n—电机转动圈数；

(ten-te(n+1))—转动一圈内的转矩差值。

累积计算稳定转速区间内的转矩波动平均值，将获得当前不平衡量的相对标示值。

依据上述的公式计算，当稳定转速内统计的转矩差值次数越多，不平衡量的计算越准确。在实际应用过程中，该时长是在相对较短的时间内进行计算，计算结果将存在偏差。偏差的产生因素是因为在不同环境电源下，电磁转矩te存在一定的偏差，计算电磁转矩的公式如下：

为了研究偏差对实际的不平衡量控制偏差，在标准环境工况中，将不平衡量的标示值记为Am，在上限工况中不平衡量的标示值记为Ah，下限工况中不平衡量的标示值记为Al，可得出如下公式：

式中：

Uh、Ul—两种上下限工况中的校正系数；

c1、c2—校正常量；

Am—标准工况环境中的基准值。

实际应用中工况的情况较复杂，不能仅通过三种工况的数据进行参数的控制，需要根据环境的变化，参数也应该相应的发生变化，最终可通过不同固定工况下的参数进行参数回归，公式如下：

最终的不平衡量A将依据环境情况UC与实际计算的不平衡量AC，进行参数拟合校正后，作为最终的不平衡量标示值。

2 系统优化设计

以某一滚筒洗衣机平台开发为例，脱水控制设计初期的方案如图2。

如图2所示，图中的不平衡量A及预设值是在标准工况下测试获取，在实际使用过程，不平衡量A的预设值设定将影响到脱水的正常运行。相同工况下，若电压偏低，不平衡量A小于预设值，存在撞筒移位的风险；若电压偏高时，不平衡量A大于预设值，存在不脱水的情况发生。鉴于初期方案的缺陷，将该问题在设计阶段进行规避设计，优化脱水控制的系统逻辑，如图3所示。

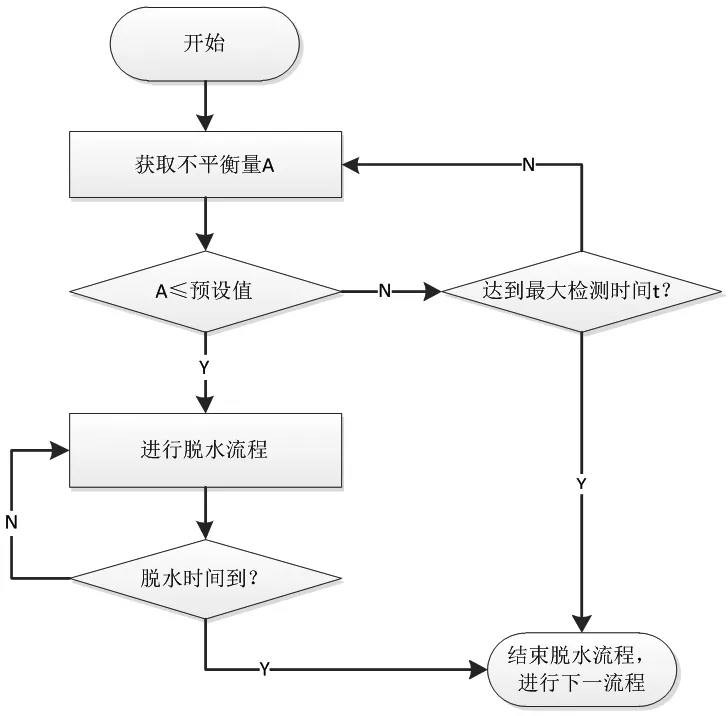
图2 设计初期方案流程图

图3 改进方案流程图

按照上述，设计脱水控制的基本流程，使得不平衡量输出值，能够随着环境的变化进行校正。系统由原来的单一输入量的控制系统，变更为双输入量控制系统，如图4和图5所示。

图4 系统优化前控制图

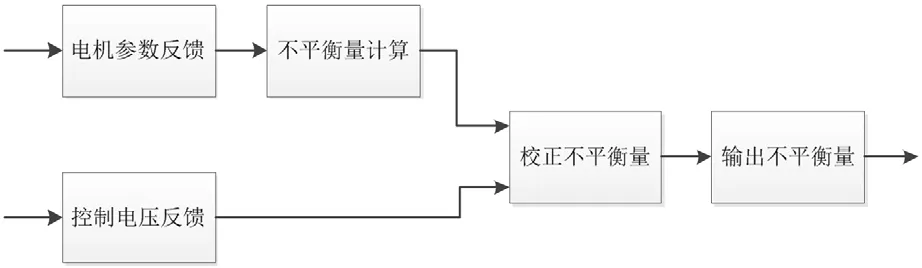
图5 系统优化后控制图

通过引入第二参数的设计方式，系统的可靠性较原控制系统提升。确保了系统参数的稳健性。

3 实验设计与数据分析

为了验证系统逻辑设计的可行性及有效性，在实验室进行了不同工况下不同状态的验证。

3.1 标准不平衡量验证

3.1.1 实验方案

将电压值作为单一环境变量，分别在上限环境工况、下限环境工况及标准环境工况下运用系统优化前后的两种方案，测试相同偏心质量下的不平衡量，对比两种方案得出的不平衡量的差异。

具体的实施方法：选用同一台洗衣机样机，依次采用空筒400 g单偏心块两种负载，运行脱水程序，采用监控程序读取样机反馈出的不平衡量；调节电压，采集不同环境工况下的不平衡量参数。

3.1.2 数据分析

采用上述实验方案测得的数据汇总于图6、图7。

图6 空筒不平衡量对比

图7 400 g单偏心块不平衡量对比

从图6可以看出，在优化前不平衡量随着电压的升高而增大，优化后的不平衡量不再随电压而改变。

就相同电压下的三组测试结果来看，优化前三组结果波动较大，易受其他环境因素的影响；而优化后相同电压下的三组测试结果极为稳定，上下偏差不会超过1。

从图7可以看出，在400 g单偏心块测试下同样能体现出优化后方案的优越性：不平衡量不再随电压的改变而变化，而且输出的不平衡量抗环境因素干扰能力也增强了。

由以上两种负载情况下的测试结果可见，优化后的不平衡量能排除电压等环境因素的影响，能够真实的反映滚筒内的不平衡状态。

3.2 模拟用户使用情况验证

3.2.1 实验方案

同样的将电压值作为单一环境变量，在同一洗衣机样机上分别采用优化前后的两种控制方案进行实负载脱水测试，对比两种方案测试结果的差异。

具体的实施方法：选用三种常见衣物组合作为试验负载，在同一台洗衣机上，分别使用优化前后两种控制，运行脱水程序，记录每组脱水的实际情况，有无撞筒移位现象发生，是否脱水成功。改变电压，验证不同环境工况下的脱水情况。

3.2.2 数据分析

采用上述实验方案测得的负载脱水情况汇总于表1。

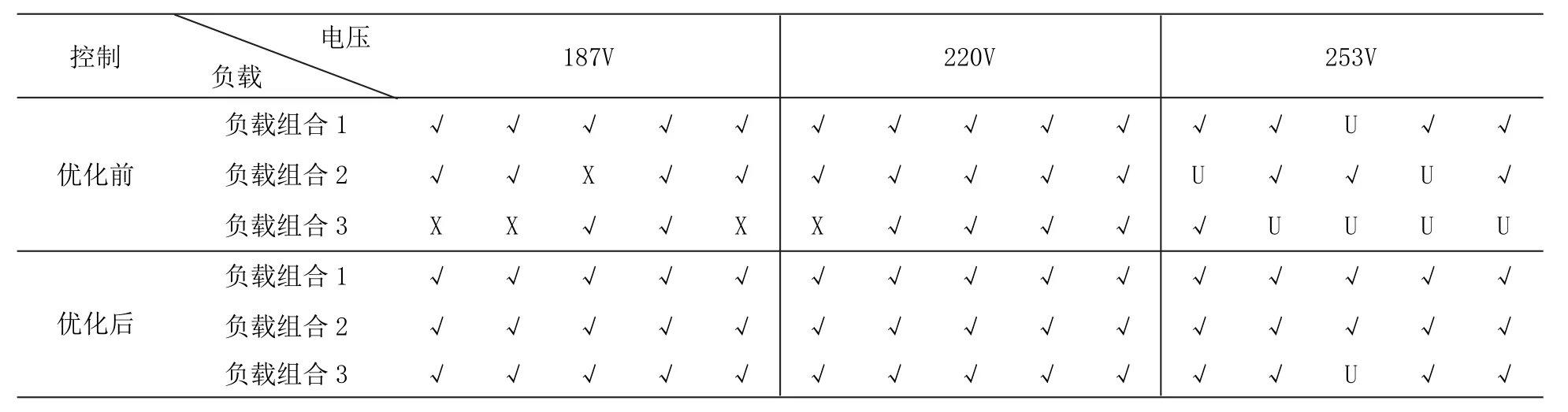
表1 实负载脱水测试

由表1可见，采用优化后的不平衡量进行脱水控制，可有效降低脱水过程中的撞筒概率，提高脱水成功率。

由图8可见，采用旧方案的脱水控制由于不平衡量的预设值仅能满足正常环境工况下的脱水，因此在低压下撞筒概率高达60 %，高压下脱水成功率仅达到20 %；而采用优化不平衡量后的控制方案，能有效避免电压等环境工况带来的影响，低压下不再撞筒，高压下的脱水成功率也提高到了80 %。

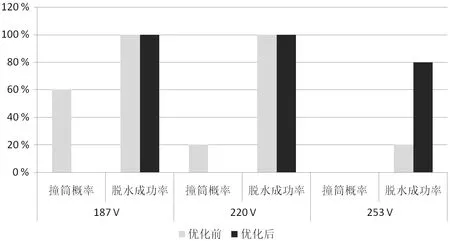
图8 负载组合3脱水测试对比

因此，优化不平衡量后的控制方案能有效解决旧方案在低电压下的撞筒问题和高电压下的脱水失败问题，可靠性较高。

4 结论

通过在标准实验工况下的数据收集与分析，针对不同工况中的不平衡量的数据回归，将该不平衡量的最终输出值稳定为不随环境电源变化的值。同时验证了该方案在实际应用过程中的情况，验证结果表明，该方法具有较高的稳定性和可靠性。解决了低压情况时撞筒移位现象及提升了高压情况时脱水完成率。本文中通过优化系统逻辑，提升了软件可靠性，解决了脱水过程的不平衡量的不可控性的问题。提升了滚筒洗衣机的整体性能，增加了产品的市场竞争能力。