HY-2B卫星散射计神经网络多区间风速反演
(1.上海海洋大学 海洋科学学院,上海201306;2.上海河口海洋测绘工程技术研究中心,上海201306)
郭 鑫1,韩 震1,2*,张雪薇1,周玮辰1
海面风场是研究海洋运动和气候变化重要的物理参数,获取高质量的海洋风场资料具有重要的意义。星载散射计是一种搭载在卫星上的主动微波传感器,是获得大范围、高时空分辨率海表风矢量最有效的方法之一。散射计发射出的电磁波束到达海面后,电磁波会发生后向散射现象。风通过调制海面的粗糙度来影响散射计的后向散射系数,而后向散射系数是风速、风向、入射角、方位角和极化方式的函数,可以建立后向散射系数与海面风矢量之间的关系,实现对海面风场的反演[1]。目前运行的散射计主要工作在C和K波段,很多地球物理模型函数(Geophysical Model Function,GMF)也是基于这2个波段建立的,比如CMOD系列和NSCAT系列[2-5]。人们对风矢量和海面几何状况之间的关系,以及电磁波与海表面之间的相互作用机制还未研究透彻,因此这些GMF都是半经验模型函数。在台风等极端情况,受海表面物理特性以及环境的复杂影响,后向散射系数与风场之间呈高度非线性关系,致使所建立的地球物理模型函数的普适性并不理想。
由于利用神经网络方法反演风速不依赖复杂的GMF,因此具有简洁高效和适应不同海况的能力[6]。Thiria等[7]于1993年将神经网络方法运用于散射计风场反演,证明了复杂传递函数可以通过使用神经网络有效地建模。宋新改等[8]于2006年基于ERS-1,ERS-2数据,采用神经网络算法对风场进行反演,推动了国内对神经网络反演海面风场的研究。Xie等[9]于2008年在考虑了海面温度对雷达后向散射系数的影响下,建立了一种基于神经网络的地球物理模型函数。Stiles等[10]于2014年开发了一种神经网络技术,用于从Ku波段散射计的测量数据中提取精确的12.5 km空间分辨率的风速。王婧等[11]在2017年使用BP神经网络对高风速风场GMF建模,并通过神经网络的订正来修正降雨对风速反演的影响。Xu等[12]2018年基于神经网络方法,联合HY-2A卫星主被动传感器(散射计和辐射计),实现了台风条件下的风场反演。
近年来,神经网络相关算法不断被优化,反向传播算法从梯度下降法、Momentum、RMSprop到Adam,网络训练的效果不断提升。随着同化技术的发展,再分析资料的质量也在提升。研究发现,欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECWMF)推出的ERA5再分析资料的适用性总体上要优于ERA-Interim[13]。本文针对当西太平洋地区存在台风的情况,基于HY-2B卫星散射计的L2A数据和ECWMF的ERA5数据,利用反向传播神经网络对其进行训练,建立多风速段的风速反演模型,并与基于NSCAT-4 GMF得的L2B风速(以下简称L2B风速,vL2B)进行了比较分析,以期通过建立合适的反演模型提高台风存在情况下的卫星散射计反演风速质量。
1 数据处理
1.1 HY-2B卫星数据
HY-2B卫星于2018-10-25成功发射升空,是我国第二颗海洋动力环境卫星。所搭载的散射计为笔形波束圆锥扫描体制,具有内、外两个波束,内波束为HH极化,入射角为41.4°,外波束为VV极化,入射角为48.5°。Wang等[14]发现HY-2B散射计风场精度优于OSCAT2和HY-2A散射计,与ASCAT相近。HY-2B散射计的L2数据由L2A和L2B数据构成,两者都以轨道为单位进行存储。L2A数据包含了风矢量单元(Wind Vector Cells,WVC)中的后向散射系数,以及相对应的入射角、方位角等信息。L2B数据包含了L2A数据基于最大似然估计方法反演得到的海面风场信息。本文中,L2A数据经过预处理后,用于神经网络模型的训练;L2B数据用于模型效果的检验。对于L2A数据,本文做两步预处理:1)统一WVC参数数量。由于每个WVC所观测的后向散射系数数目不同,为了满足神经网络输入特征一致,根据观测情况(内波束前视、内波束后视、外波束前视和外波束后视)对每个WVC的后向散射系数、入射角、以及方位角进行求和平均,使得每个单元格中具有相等数量的观测值以及仪器状态信息。2)剔除不满足实验要求数据。对于后向散射系数数目小于4以及没有同时拥有4种观测情况的单元格选择剔除;在外部条带(风矢量单元格的列索引值为[1,10]和[65,76]),只有VV极化测量,与条带的其他部分相比,质量下降,选择剔除。经过处理后,将L2A数据与L2B数据进行匹配,最终得到以风速、风向、后向散射系数、电磁波方位角、入射角为一组的同一时刻和经纬度的单元格数据。
1.2 ERA5风速数据
卫星海面风场数据和现场观测海面风场数据各有其利弊。卫星数据具有获得大范围、高时空分辨率观测值的特点,但精度不如现场观测数据;而现场观测数据虽然精度高,但数据量小(如浮标数据),在时间和空间上连续性差,很难满足神经网络训练时的数据量要求。
ERA5再分析数据是欧洲中期天气预报中心(European Centre for Medium Range Weather Forecasts,ECMWF)发布的第四代全球大气再分析产品,同化了卫星数据、现场观测数据等多种数据产品,是目前最为先进的再分析数据产品之一。陈克海等[15]对HY-2B风场数据与ECMWF再分析风场数据、浮标风场数据进行了对比,发现HY-2B风速与他们之间的误差特性基本一致。使用ERA5再分析数据的海平面10 m风速作为模型训练时的真值(以下简称ERA5风速,vERA5),具有较高精度和较高时空分辨率。由于ERA5再分析数据并没有同化HY-2B散射计数据,因此利用ERA5作为训练真值能保证数据的相对独立。
本文使用ERA5再分析数据的10 m经向风速和10 m纬向风速,其空间分辨率与时间分辨率分别为1 h和0.25°,经矢量合成后得到海平面10 m风速,再与L2A数据匹配后形成训练集,用于本文的神经网络模型训练。
1.3 L2B数据与ERA5数据对比分析
本文选取2019年发生在西太平洋的台风“海贝思”为研究对象,首先对ERA5风速和L2B风速进行匹配,匹配时,在空间上选用的是双线性插值方法,在时间上选用的是三节点插值方法。“海贝思”最强时期为10月7日至10月10日,通过获取这期间每天上午经过西太平洋地区的L2B风速,然后与ERA5风速进行时空插值,一共得到36 482组数据。
对L2B风速与ERA5风速的相关性进行分风速段分析(图1a~图1d)可知:当vERA5<4 m/s时,L2B风速与ERA5风速的均方根误差(Root Mean Square Error,RMSE)为1.98 m/s,相关系数(R)为0.27,虽然RMSE满足HY-2B散射计的技术指标(2 m/s),但相关性很差。当vERA5>24 m/s时,L2B风速与ERA5风速的RMSE为4.15 m/s,R为0.17,在相关性很差的同时,误差也超过了HY-2B散射计的技术指标。造成这种情况的主要原因是在低风速条件下(2~4 m/s),海面较为平静,对电磁波的反射主要为镜面反射,其后向散射能量较小,从而导致仪器测量信噪比较低,后向散射系数测量误差较大;在高风速段,海面后向散射系数随风速的变化越来越小,并逐渐趋于饱和[15]。因此,散射计风速反演被限制在了一定的范围内,HY-2B散射计的风速有效观测范围为4~24 m/s。当风速为中低风速时(4 m/s≤vERA5<15 m/s),L2B风速与ERA5风速的RMSE为1.44 m/s,R为0.90,当风速为中高风速时(15 m/s≤vERA5≤24 m/s),L2B风速与ERA5风速的RMSE为1.84 m/s,R为0.74。中低风速和中高风速都满足HY-2B散射计的技术指标,其中低风速的RMSE比中高风速小,且R大于中高风速。
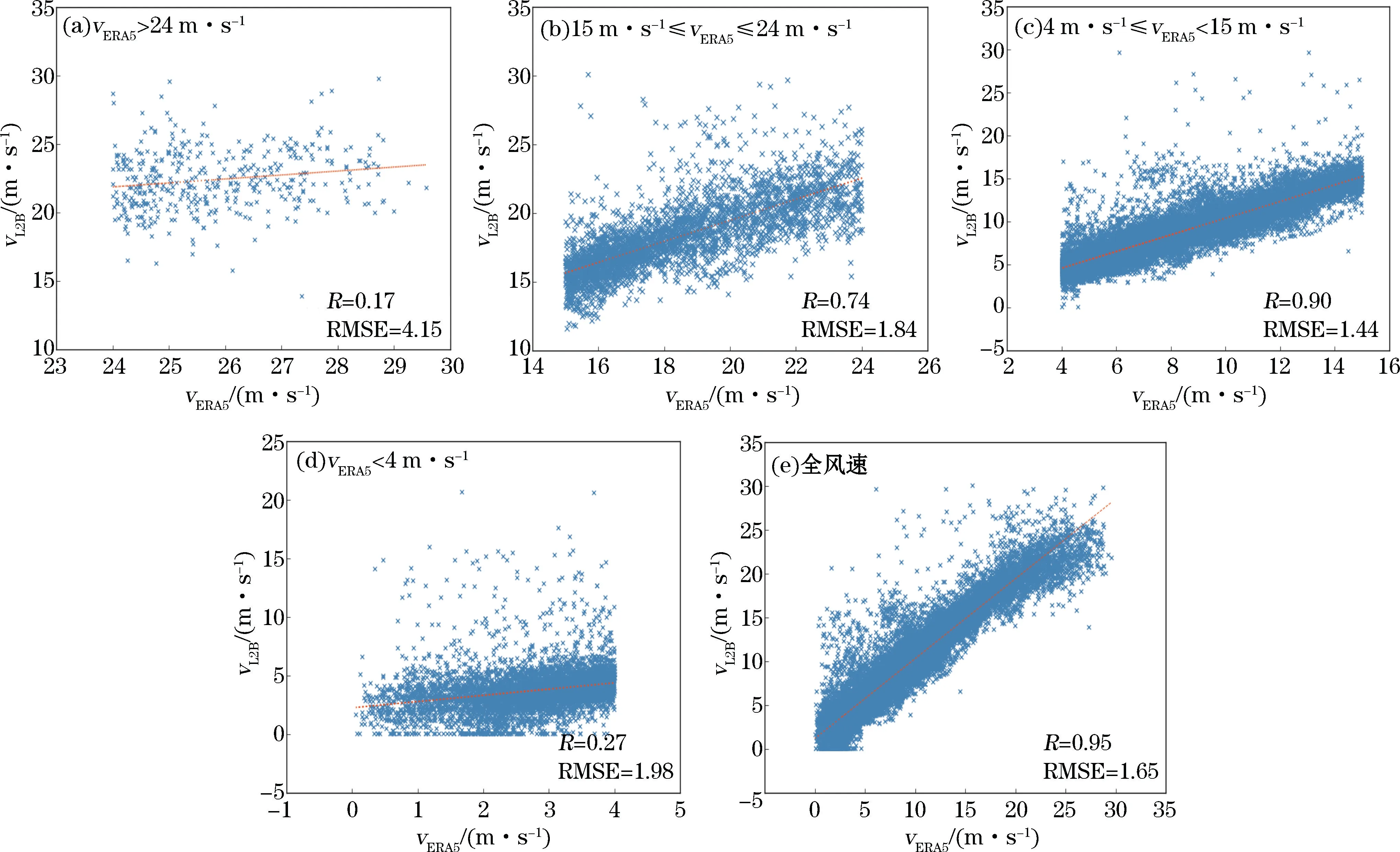
图1 L2B风速与ERA5风速相关分析Fig.1 Correlation analysis between wind speed of L2B and ERA5 wind speed
对L2B风速与ERA5风速的相关性进行总体分析(图1e)可知:在中低风速阶段,L2B风速比ERA5风速偏高,在中高风速阶段,L2B风速总体比ERA5风速偏低。此现象主要由降水所致。一般情况下,降水会使后向散射系数增大,从而使反演的风速偏大;而在大风情况下(如台风),衰减影响又起主导作用,导致反演的风速偏小[12]。
HY-2B卫星散射计的L2B风场数据由最大似然估计方法反演所得,该算法需要以某个已知的GMF为基础,L2B风场数据采用的是NSCAT-4 GMF。NSCAT-4来源于NSCAT-2,它提高了浮标与反演Ku波段散射风的一致性,特别是对于风速大于15 m/s的风。但由于当时可用的高风速数据有限,浮标观测风速和ECWMF风速也会存在一定的误差,导致NSCAT-4 GMF反演得到的风速误差在中高风速阶段大于中低风速阶段,这与图1b和图1c的分析结果一致。
通过对L2B风速与ERA5风速的对比分析,可以发现,在不同风速段,L2B风速的精度是不同的,并且影响风速精度的因素也有所不同。为了有效地避免不同因素之间的相互影响,减少非线性拟合的复杂程度,可以分风速段进行研究。在以往的研究中,可用的高风速数据有限,导致NSCAT-4 GMF对中高风速的反演精度依旧有待提高,为此,可以考虑使用其他方法进行风速反演。
2 研究方法
2.1 风速反演模型方法
人工神经网络简称神经网络,是机器学习诸多算法中的一种,能够处理高度非线性化问题。本文选取反向传播神经网络对训练集进行训练,进而建立风速反演模型。
反向传播神经网络在从输入层到输出层的过程中,通过线性求和函数和激活函数建立层与层之间的联系,不同层之间激活函数可以不同。多特征多样本量的线性求和函数为

式中,Z l为l层的线性输出;l为层数;W l为(l-1)层到l层之间各节点的权重;A l-1为(l-1)层到l层的输入值;b l为(l-1)层到l层的偏置。
激活函数是对线性输出后进行非线性运算,将非线性特性引入网络中。常用的激活函数有Sigmoid函数、tanh函数和Re LU函数,3个函数的公式为

经过激活函数,Z l转换为A l后再作为下一层的输入值,进行下一层的线性函数和激活函数处理,直到输出层输出结果。得到向前传播结果后,在进行反向传播前,利用成本函数计算网络输出值与真实值之间总体误差。在回归问题中,常采用均方误差(Mean Squared Error,MSE)作为神经网络的成本函数,成本函数的计算公式为

式中,A l-last为神经网络的输出值,y∧为真实值,N为样本个数。
确定成本函数后,利用误差反向传播算法对网络的权重和偏置(统称为参数θ)进行更新,误差反向传播算法公式为

式中,θ为更新前参数,θ′为更新后参数,η为学习率,∇θ为梯度算子。
通过前向传播和误差反向传播的交替进行,不断更新各个节点的权重和偏置,使得成本函数最小化:
反向传播神经网络算法通过找到使成本函数最小化的参数θ,从而建立使输出结果与真实结果误差最小的网络模型,以达到非线性拟合的目的。
2.2 模型检验指标
采用均方误差(MSE)、平均绝对值误差(MAE)和相关性系数(R)等统计指标对模型的性能进行评估。MSE,MAE和R的具体计算公式如下:

式中,N为样本量为第i个模型输出值,y i为第i个真实参考值为模型输出值的平均值为真实参考值的平均值。
3 网络训练
3.1 建立网络框架
反向传播神经网络一般由输入层、隐藏层和输出层组成。其中输入层一共有20个节点,每个风矢量单元格包括4组数据,每组数据包括后向散射系数(σ)、电磁波入射角的正余弦值(sinλ,cosλ)、电磁波方位角与风向的夹角的正余弦值(sinχ,cosχ)这5个特征。输出层为1个节点,即风速值,如图2所示。

图2 神经网络结构Fig.2 Structure of neural network
神经网络中的参数设置依据隐藏层数、隐藏层节点数、学习率、mini-batch大小和激活函数。
1)隐藏层数。当隐藏层数为2层,通过激活函数可以表示各种精度的决策边界,并且可以拟合各种精度的平滑映射。
2)隐藏层节点数。隐藏层节点数的确定采用了经验公式[16],该经验公式为

式中:Ni是输入层神经元个数;No是输出层神经元个数;Ns训练集的样本数;α为可调参数,通常取2~10。经过调试,发现当α=8时,即当节点数为173时,训练效果最好。
3)学习率。通过对不同学习率的网络进行训练,发现学习率为0.01时,模型能够收敛到最小值附近,且收敛的速度较快。
4)mini-batch大小。当mini-batch大小是2n,代码运行较快。
5)激活函数。隐藏层采用Sigmoid函数,输出层采用ReLU函数。Re LU函数使得模型的输出值大于0(风速值为正),避免了梯度爆炸和梯度消失问题,防止了参数无法更新,并加快了网络训练速度。
3.2 数据集的划分
当5 m/s<vERA5<15 m/s时,海面对电磁波的后向散射和海面风场之间有很好的对应关系[17]。当风速超过15 m/s时,可能产生波浪破裂并与海面气流分离等现象,对海面粗糙度造成影响,从而使影响海面后向散射系数的因素多样化[18]。因此,根据HY-2B散射计的有效风速范围(4~24 m/s),本文将进行3次不同的神经网络训练,分别为全风速神经网络训练(4 m/s≤vERA5≤24 m/s)、中低风速神经网络训练(4 m/s≤vERA5<15 m/s)以及中高风速神经网络训练(15 m/s≤vERA5≤24 m/s)。全风速共有29 199组数据、中低风速共有25 739组数据,中高风速共有3 460组数据。训练集和测试集以8∶2的比例进行随机抽取。在训练过程中,训练数据每遍历网络一次就从训练集中随机抽取20%数据作为验证集进行验证。
本文使用核密度估计[19]方法来查看数据的分布情况。核密度估计是非参数估计中的一种,相较于参数估计,它不加入任何先验知识,而是根据数据本身的特点、性质来拟合分布。由图3(纵坐标为观测数据落在某一风速区间的概率值,横坐标为风速区间)可知,3种神经网络模型训练集和测试集的核密度分布相似,符合训练要求。
为了保证网络的收敛效果,在进行训练前,对数据进行标准化。标准化可以在不清楚各个维度的相对重要程度之前,让输入的各个维度分布相近。本文使用Z-score标准化[20]对训练集进行处理。

图3 不同风速范围下训练集和测试集的核密度估计Fig.3 Nuclear density estimation of training set and test set under different range of wind speeds
3.3 训练结果
进行网络框架的构建、参数设置,以及数据集的预处理后,开始对网络进行训练。随着训练数据遍历网络次数(Epoch)的增加,模型输出值与真实值的总体误差将逐渐减少。在模型训练过程中,如果连续30次验证集的均方误差(MSE)不再下降,则停止训练。由各风速模型训练时绝对值误差与均方误差的走势(图4)可知,随着训练次数的增加,训练集和验证集的均方误差和绝对值误差逐渐下降,并最终趋于稳定。

图4 各风速模型训练时绝对值误差与均方误差的走势Fig.4 The trend of absolute value error and mean square error during training of different wind speed model
训练结束后,采用平均绝对误差和均方误差评估模型性能。在中高风速中,L2B风速与ERA5风速的平均绝对值误差(MAE)为1.29 m/s,均方误差(MSE)为3.25 m/s;模型反演风速与ERA5风速的MAE为0.27 m/s,MSE为0.18 m/s。在中低风速中,L2B风速与ERA5风速的MAE为0.95 m/s,MSE为2.10 m/s;模型反演风速与ERA5风速的MAE为0.24 m/s,MSE为0.14 m/s。在全风速中,L2B风 速 与ERA5风 速MAE为0.99 m/s,MSE为2.22 m/s;模型反演风速与ERA5风速的MAE为0.34 m/s,MSE为0.32 m/s,如表1所示。
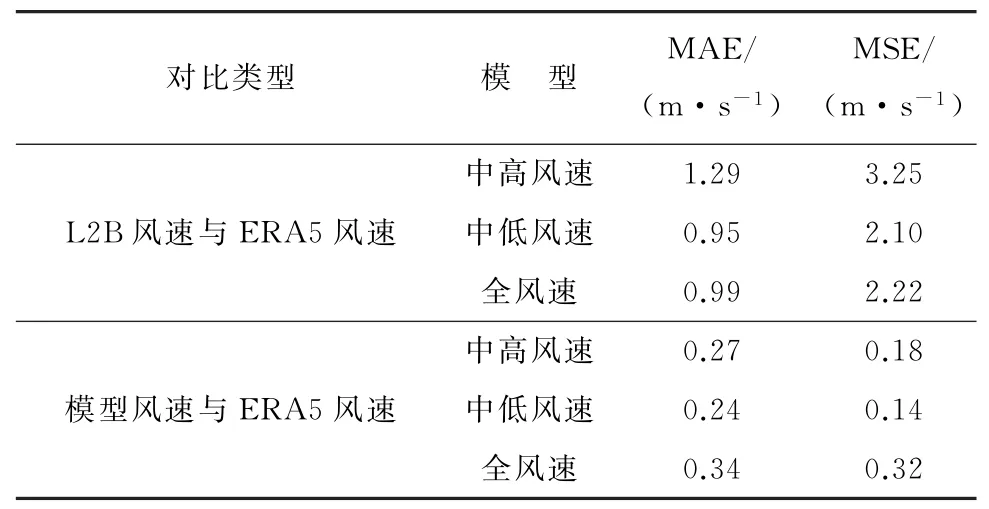
表1 各模型训练集反演风速误差情况Table 1 Wind speed inversion errors from training set different each models
由L2B风速和各模型训练集反演风速与ERA5风速的相关分析(图5)可知,在中高风速中,L2B风速与ERA5风速相关系数(R)为0.75;模型反演风速与ERA5风速R为0.99。在中低风速中,L2B风速与ERA5风速R为0.89;模型反演风速与ERA5风速R为0.99。在全风速中,L2B风速与ERA5风速R为0.94,模型反演风速与ERA5风速R为0.99。
从模型的训练效果来看,不同模型反演得到的风速与ERA5风速相关系数(R)都达到0.99。全风速模型的MSE最高(0.32 m/s),其次是中高风速模型(0.18 m/s),中低风速模型最小(0.14 m/s)。由此可见,对于在不同风速段下建立的神经网络模型,网络性能的表现有所不同。造成这种现象的原因可能是:在不同的风速段下,影响后向散射系数与风速之间的映射关系的因素有所不同,将不同风速段放在一起训练时,后向散射系数与风速之间的映射关系变得更加复杂。中低风速模型的MSE和MAE比中高风模型风速小,这可能是由中高风速模型包含了更多的台风信息、拟合情况更加复杂所致。
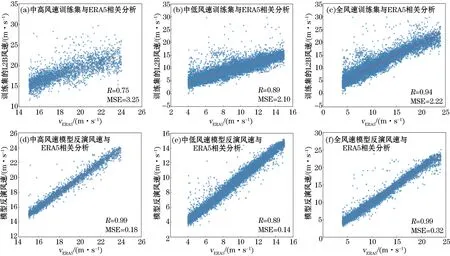
图5 在训练集中v L2B与v ERA5的相关分析以及各模型反演风速与v ERA5的相关分析Fig.5 The correlation analysis between v L2B and v ERA5,as well as the correlation analysis between wind speed inversion resutts of each model and v ERA5 in the training set
3.4 测试结果
为进一步验证模型的有效性,利用测试集对模型的泛化能力进行测试。结果(表2)表明,在中高风速段,L2B风速与ERA5风速的MAE为1.38 m/s,MSE为3.99m/s;模型反演风速与ERA5风速的MAE为0.48 m/s,MSE为0.54 m/s。在中低风速段,L2B风速与ERA5风速MAE为0.95 m/s,MSE为2.00 m/s;模型反演风速与ERA5风速的MAE为0.35 m/s,MSE为0.27 m/s。在全风速段,L2B风 速 与ERA5风 速MAE为1.02 m/s,MSE为2.29 m/s;模型反演风速与ERA5风速的MAE为0.42 m/s,MSE为0.46 m/s。
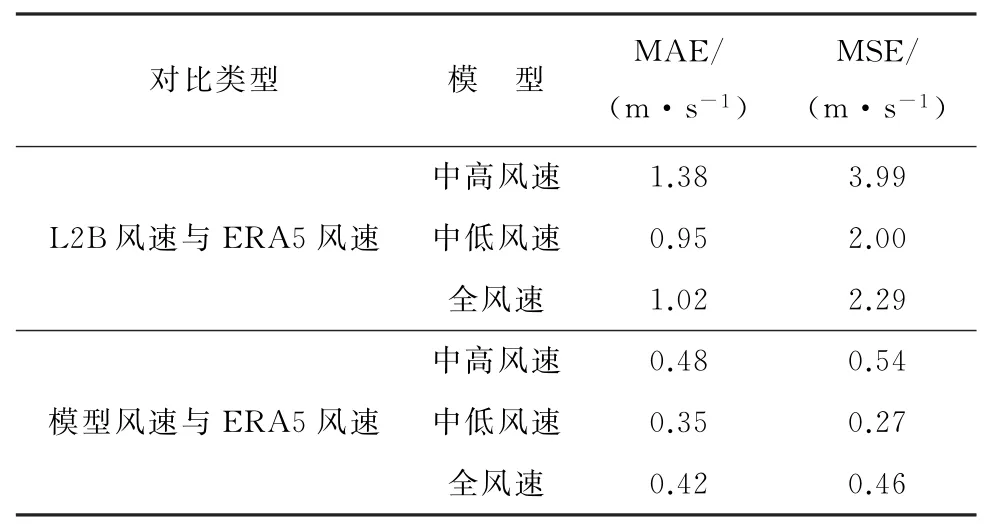
表2 各模型测试集反演风速误差情况Table 2 Wind speed inversion errors from test set of different models
由L2B风速和各模型测试集反演风速与ERA5风速的相关分析(图6)可知:在中高风速中,L2B风速与ERA5风速相关系数(R)为0.71;模型反演风速与ERA5风速R为0.95。在中低风速中,L2B风速与ERA5风速R为0.90;模型反演风速与ERA5风速R为0.98。在全风速中,L2B风速与ERA5风速R为0.94,模型反演风速与ERA5风速R为0.99。全风速和中低风速模型反演的风速与ERA5风速的R都超过了0.98,而中高风速模型的R从训练集时的0.99下降到了0.95。在MSE方面,中高风速模型MSE最高(0.54 m/s),其次是全风速模型(0.46 m/s),中低风速模型最低(0.27 m/s)。在测试集中,全风速模型的MSE低于中高风速模型,与训练集的情况相反;中低风速模型的MSE依旧最低;综合相关系数和均方误差来看,高风速模型的泛化能力弱于其他2种模型,这可能由高风速下的训练和测试样本较少所致。整体来看,3种网络模型都有很好的泛化能力。

图6 在测试集中v L2B与v ERA5的相关分析以及各模型反演风速与v ERA5的相关分析Fig.6 The correlation analysis between v L2B and v ERA5,as well as the correlation analysis between wind speed inverison results of each model and v ERA5 in the test set
4 结 论
针对西太平洋地区有台风存在的情况,以ERA5风速为真实风速参考值,基于HY-2B卫星散射计数据,利用神经网络方法进行风速反演。受物理机制的制约,在vERA5<4 m/s和vERA5>24 m/s情况下,利用后向散射进行风速反演不再有效。作为神经网络训练时的输入特征,过低或过高风速下的后向散射值会对模型训练造成不利影响,因此选择在有效风速内的后向散射值进行模型训练。由于不同风速段内影响风速反演的环境因子不同,因此分别建立全风速(4 m/s≤vEAR5≤24 m/s)、中低风速(4 m/s≤vEAR5<15 m/s)、以及中高风速(15 m/s≤vEAR5≤24 m/s)三种不同的风速反演模型。通过对模型反演结果的对比分析,得到结论:
1)3种风速反演模型的MSE和MAE优于基于NSCAT-4 GMF得到的L2B风速的MSE和AME,训练结果和测试结果都有良好的表现,其中中低风速模型的MSE和MAE最低,中高风速模型的MSE和MAE降低幅度最大。
2)对比训练集和测试集,虽然3种反演模型在测试集中的MSE和MAE都有所升高,但依旧优于L2B风速。
3)相比于全风速,对风速进行分区间所建立的反演模型效果更好,虽然中高风速模型在测试集中的误差大于全风速模型,但这可能是由中高速模型测试集数据较少所致。
相比于L2B风速,利用本文模型反演的风速MSE和MAE都有所下降,同时相关系数(R)有所增加,主要得益于3种因素:神经网络强大的非线性拟合以及泛化能力;通过分区间进行反演,避免了影响不同区间后向散射因素的相互影响;将ERA5作为真实风速参考值,具有较高精度和较高时空分辨率的特点,能够更好地模拟真实风速。然而,由于中高风速模型的训练数据较少,因此泛化能力相比于其他2种模型较弱,在今后的工作中,我们将增加中高风速的样本数量以优化中高风速模型。

